本帖最后由 勃失败 于 2024-10-10 06:44 编辑
在参与 Max-Cut 最大割游戏的这段奇妙旅程中,我经历了多次的思考、尝试与突破。当最终成功解出全部游戏答案的那一刻,心中的喜悦与成就感难以言表。现在,我想与大家分享一下我的解题思路和这段独特经历带来的感想。
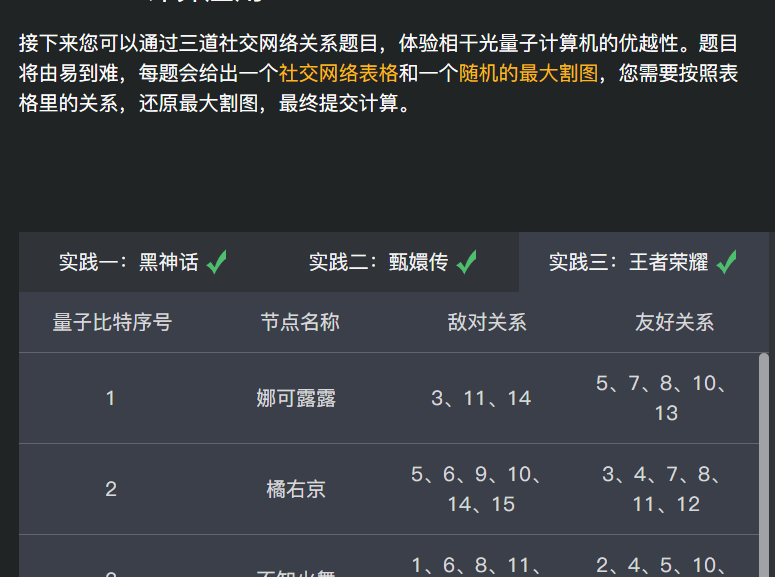
一、解题思路
Max-Cut 问题的核心是将给定无向图的顶点集划分成两个子集,使得连接这两个子集的边的数量最大。首先,我花了大量时间仔细研究问题的定义和性质,明确目标是最大化割边的数量。
一开始,我选择了贪心算法作为我的主要解题方法。贪心算法的优势在于简单直观,容易上手。贪心算法是一种简单直观的方法。它从一个初始的划分开始,通常是随机地将一个顶点放入一个子集,然后逐步考虑其他顶点。对于每个未划分的顶点,计算将其放入子集S或V - S时,割的大小的增加量。选择能使割的大小增加最多的划分方式。
举个例子,假设我们有一个简单的图,顶点为v_1,v_2,v_3,边为(v_1,v_2),(v_2,v_3),(v_1,v_3)。我们随机将v_1放入S。然后考虑\_2,如果将v_2放入S,割的大小不变;如果将v_2放入V - S,割的大小增加2(因为有两条边连接v_1和v_2以及v_2和v_3),所以我们将v_2放入V - S。接着考虑v_3,如果将v_3放入S,割的大小增加1(因为有一条边连接v_1和v_3);如果将v_3放入V - S,割的大小增加1(因为有一条边连接v_2和v_3),我们可以选择一种划分方式。贪心算法在某些情况下可以快速得到一个较好的解,但不能保证得到最优解。
我随机选择一个顶点放入其中一个子集,然后依次考虑其他顶点,根据将该顶点放入不同子集时割边数量的增加量来决定其归属。通过不断地重复这个过程,逐步构建出两个子集的划分。然而,贪心算法虽然速度快,但不能保证得到全局最优解。在一些简单的图上,贪心算法能够快速给出一个较好的结果,但对于更复杂的图结构,可能会陷入局部最优解。
为了寻求更好的解决方案,我开始研究半定规划方法。通过引入一些辅助变量和约束条件,将原问题转化为一个可以用多项式时间算法求解的问题。然后利用半定规划求解器得到一个松弛问题的解。最后通过一些随机化或舍入技术,将松弛问题的解转化为原Max - Cut问题的一个可行解。 对于给定的图G,我们定义一个矩阵变量X,并根据图的结构和Max - Cut问题的目标函数建立相应的半定规划问题。通过求解这个半定规划问题,我们得到一个关于X的解。然后通过一些特定的舍入算法,比如Goemans - Williamson舍入算法,将这个解转化为原问题的一个划分方案,从而得到一个割的大小的估计值。这种方法通常可以得到比贪心算法更好的解,但计算复杂度相对较高。虽然半定规划方法通常能够得到比贪心算法更好的结果,但计算复杂度相对较高,需要一定的数学基础和计算资源。
我还了解到了量子算法在解决 Max-Cut 问题上的潜力。对于Max - Cut问题,它利用量子比特来表示顶点的划分状态。通过在量子系统上施加一系列的量子门操作,这些操作由参数化的角度来控制。然后通过测量量子系统,得到一个经典的划分方案。通过调整参数,优化测量结果,以期望得到一个较好的割的大小。 我们初始化量子比特来表示图的顶点。然后应用一系列的量子门,比如旋转门和纠缠门等。这些门的操作由一些参数决定。经过多次迭代的操作和测量,我们尝试找到一组最优的参数,使得得到的割的大小最大。量子算法在处理一些复杂的Max - Cut问题时,有可能在多项式时间内得到较好的解,尤其是对于大规模的图,它可能具有潜在的优势。量子近似优化算法(QAOA)等量子算法利用量子比特来表示顶点的划分状态,通过在量子系统上施加一系列的量子门操作和测量,尝试找到最优的参数以得到较好的割边数量。虽然目前量子算法在实际应用中还面临着诸多挑战,但它为未来解决复杂的 Max-Cut 问题提供了一种新的思路和可能性。
在实际解题过程中,我并没有局限于一种方法,而是尝试综合运用贪心算法、半定规划方法和对量子算法的理解。我先用贪心算法快速得到一个初始解,然后利用半定规划方法对这个解进行优化。同时,不断思考如何根据图的结构特点选择合适的方法和策略,以提高解题效率和准确性。
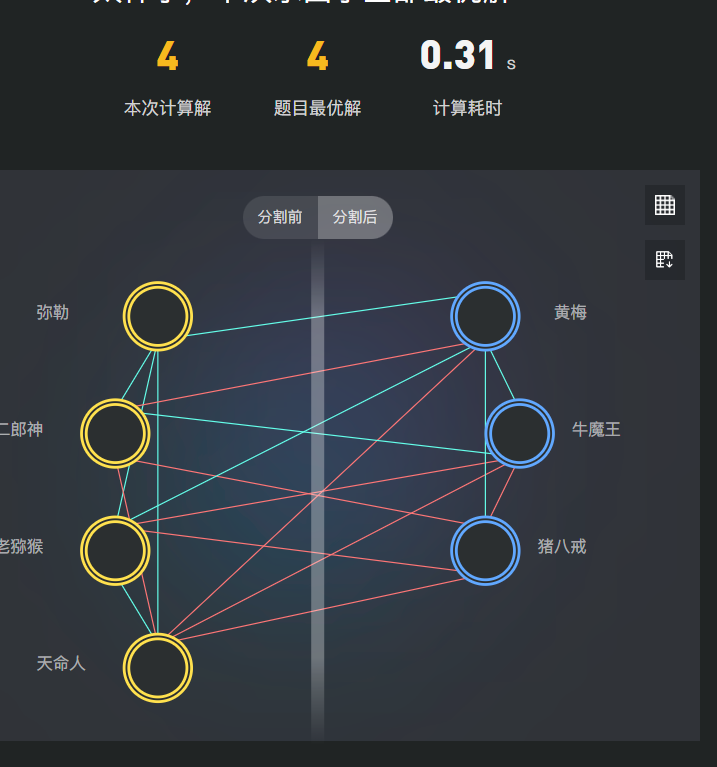
二、感想与体会
这个游戏是一个充满挑战的智力挑战,它让我深刻体会到了解决复杂问题的艰辛与乐趣。在这个过程中,我不断地学习新的知识和算法,拓展了自己的思维方式和解决问题的能力。每一次的失败都是一次学习的机会,让我更加深入地理解问题的本质和各种方法的优缺点。
Max-Cut 问题的解决不仅是一个数学挑战,也是对科技发展的一次见证。从传统的贪心算法到先进的半定规划方法和量子算法,科技的不断进步为我们提供了更多解决复杂问题的工具和思路。这让我对未来科技的发展充满了期待,也激发了我对科学研究的热情。
总之,参与 Max-Cut 最大割游戏是一次难忘的经历。通过这次挑战,我不仅成功解出了全部游戏答案,还收获了知识、成长和对科技的热爱。我希望我的解题思路和感想能够对其他闯关者有所帮助,让我们一起在科技的海洋中继续探索和前行。 | 



























