本帖最后由 Dorian 于 2025-1-23 17:32 编辑
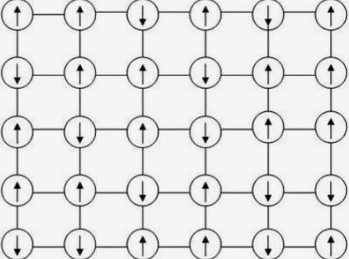
以“等概率原理”作为唯一基本公理发展出来的统计力学相较于理论物理的其它分支有着更为扎实和严格的理论基础。由它导出的正则系综下的配分函数是由诸多性质足够良好的在全平面解析的指数函数相加而成。进而体系的各种热力学量和响应函数(热力学涨落)都可以直接通过对该正则配分函数取对数后求一阶或二阶偏导数或者它们的组合得到。所以按理说各种热力学量和响应函数应当完全没有奇异性,因为像这样数学性质如此之好的在全平面解析的配分函数在取完对数和执行完有限次的求导运算后理应还是性质足够良好的解析函数。然而真实世界里发生的相变过程却对应于热力学量或响应函数的奇异性(非解析性)!所以一个很自然的问题就是:统计力学究竟能否描述相变?答案是肯定的!之前的分析之所以无法给出相变是因为我们已经隐含地假设体系的自由度个数是有限的,所以配分函数只是有限个指数函数的和(对应一个部分和),没有任何的奇异性,进而由它衍生出的各种热力学量和响应函数当然也没有奇异性。然而如果当体系的自由度个数趋向于无穷大,也就是当体系处于热力学极限的情形下,此时配分函数就是无穷个指数函数的和(对应一个无穷级数)。而无穷级数相较于部分和在数学性质上有着本质的不同!尽管构成这个无穷级数的每一项都是解析函数,但无穷个解析函数的和却不一定是解析函数!它在某些点或区域有可能会表现出奇异性,进而由它衍生出的各种热力学量和响应函数也会呈现出相应的奇异性。这些奇异性也就对应着相变的发生。本文仅以统计力学中最简单但却最重要的相互作用模型(Ising模型)为例,对相变问题做一些初步的探讨,包括一维和二维Ising模型的严格解,平均场近似下Ising模型的近似解,和重整化群框架下对一维Ising模型的再分析。Ising模型的重要性体现在(1)统计力学的很多模型都是建立在Ising模型的基础上或者是以Ising模型为原型的(比如Heisenberg模型,二维XY模型),(2) 许多看似与Ising模型完全没关系的系统,比如气液连续相变,在相变临界点处的行为和Ising模型的完全一致,所以Ising模型具有广泛的普适性。Ising模型不仅在统计力学里有着举足轻重的地位,它也极大地启发并促进了现代量子场论,共形场论和弦论的发展。
一、一维Ising模型的严格解 ——有限温下不存在相变
考虑N个两能级自旋磁矩排成一条一维的链。规定外加磁场B的方向叫z方向,则处于这个一维链上每个格点的自旋磁矩与外磁场耦合的塞曼能是:

其中 是玻尔磁子。 是玻尔磁子。 是泡利算符 是泡利算符 的本征值(因为此时我们考虑的是两能级体系,所以只对应2个本征值)。所以N个自旋磁矩与外磁场耦合的总塞曼能是: 的本征值(因为此时我们考虑的是两能级体系,所以只对应2个本征值)。所以N个自旋磁矩与外磁场耦合的总塞曼能是:

除了磁矩与外磁场耦合出的塞曼能,我们同时考虑格点间磁矩与磁矩间的相互影响,即所谓的相互作用能。为简单起见,只考虑最近邻磁矩间的相互作用。这个相互作用的形式正比于一个具有能量量纲的交换积分常数 (这个结论可以从量子力学导出)和两相邻格点上自旋的乘积。进一步假定系统在低温下更倾向于磁矩间相互正平行的排列方式,因为这种排列方式对应的能量比反平行方式排列对应的能量更低。所以总的磁矩间的相互作用能可以写成: (这个结论可以从量子力学导出)和两相邻格点上自旋的乘积。进一步假定系统在低温下更倾向于磁矩间相互正平行的排列方式,因为这种排列方式对应的能量比反平行方式排列对应的能量更低。所以总的磁矩间的相互作用能可以写成:

对一维链的情形,每个磁矩只和它最近邻的左右两个磁矩间存在相互作用。然而,注意到第一个和最后一个磁矩由于处在一维链的边界处,所以只有来自一侧的相互作用。这个问题使得首尾两个磁矩与中间的磁矩并不等价。为了解决这个问题使得体系具有更好的平移对称性,我们可以采取周期性的边界条件。在一维的情形就是链的首尾相接变成一个环,所以上述的 在一维周期性边界条件的约束下可以写成: 在一维周期性边界条件的约束下可以写成:

所以这个一维链(环)体系的总哈密顿量就是塞曼能和相互作用能之和:

由于此时的微观状态构型空间  的自由度是分立的,所以体系的正则配分函数是: 的自由度是分立的,所以体系的正则配分函数是:

其中 是如下矩阵: 是如下矩阵:

 和 和  (此处不妨规定 (此处不妨规定 > > )是 )是 的两个本征值。 的两个本征值。
由于体系的粒子数N很大(仅1mol物质中  ,所以可以认为 ,所以可以认为  ,即体系处于热力学极限状态),又因为我们已经假设了 ,即体系处于热力学极限状态),又因为我们已经假设了 > > ) )
,所以体系的亥姆霍兹自由能可以写成: 
所以体系的总平均磁矩是:

所以下面的目标就是计算 ,即矩阵 ,即矩阵 较大的本征值。然后由此去计算M。经过一些繁杂的计算我们最终可以得到: 较大的本征值。然后由此去计算M。经过一些繁杂的计算我们最终可以得到:

考虑自发磁化(即外磁场  的极限情况)。在有限温情形下, 的极限情况)。在有限温情形下, ,此时 ,此时 是个大于0的有限值。所以任意有限温下总的平均磁矩是: 是个大于0的有限值。所以任意有限温下总的平均磁矩是:

在绝对零温时, ,总的平均磁矩是: ,总的平均磁矩是: 
所以,在任意有限温下体系的平均磁矩都是0(也就是都处于顺磁相)!仅在绝对零度这一点时体系才有非零的平均磁矩(也就是处于铁磁相)!也就是说,一维的Ising模型在任意有限温下都不存在由顺磁相到铁磁相的相变过程!所以到此为止我们严格地论证了一维Ising模型不存在自发磁化!历史上Ising在第一次得到这个一维体系无相变的结果后就天真地以为对于二维,三维,甚至是更高维的体系都不存在相变,并由此得出了一个错误的“结论”:统计力学大概不能描述相变。然而我们下面可以看到,对于二维或者更高维的Ising模型通过统计力学的手续其实是可以给出相变的。
二、 二维Ising模型的严格解 — 有限温下存在相变
考虑和第一节基本完全相同的问题,除了把自旋磁矩的排列方式从长度是N的一维链变成一个规格是 的二维正方格子。在统计力学的框架下,对二维正方格子的Ising模型的正则配分函数的严格求解比一维Ising模型的求解要复杂得多(历史上不加外磁场B的严格解最先由数学奇才Onsager给出,后来杨振宁给出了在弱场B下二维Ising模型的严格解,并给出了1/8这一平均磁化对应的临界指数)。所以这里略去中间求解正则配分函数的繁杂过程,直接给出在外磁场B=0时,对二维正则配分函数取对数后得到亥姆霍兹自由能的表达式是: 的二维正方格子。在统计力学的框架下,对二维正方格子的Ising模型的正则配分函数的严格求解比一维Ising模型的求解要复杂得多(历史上不加外磁场B的严格解最先由数学奇才Onsager给出,后来杨振宁给出了在弱场B下二维Ising模型的严格解,并给出了1/8这一平均磁化对应的临界指数)。所以这里略去中间求解正则配分函数的繁杂过程,直接给出在外磁场B=0时,对二维正则配分函数取对数后得到亥姆霍兹自由能的表达式是:


其中 
自发磁化对应的相变临界点应该出现在对应的亥姆霍兹自由能函数奇异(发散)的地方。自由能函数的头两项在有限温一定是解析的。所以自由能函数的奇异性必定出现在双求和号里的 项在其宗量是0的时候。我们可以由此定出相变临界温度: 项在其宗量是0的时候。我们可以由此定出相变临界温度: 所以完全不同于一维Ising模型的结论,二维正方格子的Ising模型在有限温下存在相变!统计力学的确可以描述相变! 所以完全不同于一维Ising模型的结论,二维正方格子的Ising模型在有限温下存在相变!统计力学的确可以描述相变!
三、任意维数下Ising模型的近似解(平均/自洽场近似)— 有限温下存在相变
上面我们分别给出了一维和二维Ising模型的严格解。然而对于二维以上的Ising模型目前还不存在严格解,但我们可以利用平均场的方法来获得近似解。根据之前第一节中的分析可以写出任意维度下Ising模型的哈密顿量:

假设每个格点有z个最近邻的格点(即配位数=z)。比如对于正方格子,z=2d,其中d是体系所在空间的维数。现在我们对相互作用项(哈密顿量中的第一项)采取平均场近似,即把与格点i最近邻的z个格点上的自旋(被 j 标记)作为对格点 i 的等效平均外场处理。这个外场由体系本身的状态自洽决定(注意这个自洽过程是个逐步迭代的非线性过程)。将每个格点上自旋  的平均值用 的平均值用  表示,则体系哈密顿量可以被近似等效成: 表示,则体系哈密顿量可以被近似等效成:

所以在经过了平均场近似后,相邻自旋间复杂的相互作用已经被考虑到等效的外场里了。所以原先棘手的相互作用体系变成了一个等效的我们容易处理的”无相互作用体系“!下面考虑在此哈密顿量所定义的正则系综分布下每个格点上自旋的平均值:

因为整个迭代过程必须自洽,即方程左边计算出的格点自旋平均值必须与方程右边等效外场里预设的自旋平均值自洽即 ,所以我们可以得出格点自旋平均值满足的非线性自洽方程: ,所以我们可以得出格点自旋平均值满足的非线性自洽方程:

考虑自发磁化(即外场B=0时的平均自旋磁矩),自洽方程简化为:

因为这是个超越方程,所以我们只能通过直观作出方程左右两侧的函数图像来解它。根据图1和图2,容易发现当 时,方程只有 时,方程只有  的唯一解,对应平均自旋磁矩为0(没有磁化); 的唯一解,对应平均自旋磁矩为0(没有磁化);


当  时,根据图3,方程有三个解,一个是 时,根据图3,方程有三个解,一个是  ,另外两个互为相反数的非零解完全等价,因为B=0时Ising模型的哈密顿量具有分立的 ,另外两个互为相反数的非零解完全等价,因为B=0时Ising模型的哈密顿量具有分立的  对称性。 对称性。

为了判定在  时到底取 时到底取  的解还是 的解还是  的解,我们必须比较它们亥姆霍兹自由能的相对大小,然后取自由能更小的状态作为体系应当处在的稳定状态。当外磁场B=0时,自由能关于平均自旋磁矩的函数可以写成 的解,我们必须比较它们亥姆霍兹自由能的相对大小,然后取自由能更小的状态作为体系应当处在的稳定状态。当外磁场B=0时,自由能关于平均自旋磁矩的函数可以写成

为了直观,图4作出了自由能F关于 的函数曲线草图: 的函数曲线草图:

从图4很容易看出  相较于 相较于  对应更大的自由能F。所以是一个不稳定解(亚稳态),即任何一个微小的扰动都会让体系跑到 对应更大的自由能F。所以是一个不稳定解(亚稳态),即任何一个微小的扰动都会让体系跑到 的稳定状态。所以当 的稳定状态。所以当 时,,我们只能取 时,,我们只能取  的解,这对应到平均自旋磁矩非零(非零磁化)!所以综合起来,我们发现:在温度T逐渐下降至跨越特征温度 的解,这对应到平均自旋磁矩非零(非零磁化)!所以综合起来,我们发现:在温度T逐渐下降至跨越特征温度  的时候,体系经历了从 的时候,体系经历了从 (零磁化,对应无序相)到 (零磁化,对应无序相)到  (非零磁化,对应有序相)的转变。所以 (非零磁化,对应有序相)的转变。所以  这个特征温度就是平均场近似下顺磁-铁磁相变发生的温度(也叫做“临界温度”)!对于一维,二维,三维情形这几个特殊情形,平均场近似下顺磁-铁磁相变发生的临界温度分别是: 这个特征温度就是平均场近似下顺磁-铁磁相变发生的温度(也叫做“临界温度”)!对于一维,二维,三维情形这几个特殊情形,平均场近似下顺磁-铁磁相变发生的临界温度分别是:

容易发现,平均场近似预言一维Ising模型存在非零的相变温度。而这与之前第一节中我们通过严格解得到的一维Ising模型不存在有限温相变的结论完全矛盾!这意味着平均场近似在一维情形下给出了定性上完全错误的结论!这个错误结论产生的根本原因是平均场近似完全忽略了热涨落对体系的影响,而在一维的情形,热涨落又是极其重要不可忽略的因素。对于二维情形,由于热涨落的影响变小,平均场近似和之前第二节中二维Ising模型的严格解得到的结论从定性上来看是完全正确的:两者都预言了有限温下相变的存在。只不过从定量上来看,还是由于热涨落的影响,平均场近似把真实的相变温度估计高了!但随着空间维数的持续增加,热涨落对体系的影响会进一步变小,所以平均场近似下给出的临界相变温度会变得越来越准确!
为了更加直观地看出上面描述的平均磁化  随温度T的变化关系,下面依据原始的自洽方程,作出平均场近似下的 随温度T的变化关系,下面依据原始的自洽方程,作出平均场近似下的  的函数草图: 的函数草图:

四、 利用重整化群理论导出一维Ising模型在有限温下不存在相变
下面我们重新回到一维Ising模型。不过这次我们不像第一节那样直接去求解配分函数。相反,我们的思路是:只是形式上地写出配分函数,然后利用相变发生时体系涌现出的自相似性的特征对配分函数在不同空间尺度上的数学形式进行限制,从而确定出相变临界点。
根据一维Ising模型的哈密顿量:

我们可以写出体系正则配分函数的数学形式是:

其中描述体系耦合常数的一组初始值分别是  。现在将构成体系的N个自旋划分成N/2个互不相交的集团,每个集团内部有2个自旋。相邻集团间有相互作用。将每个集团内部的第二个自旋的自由度求和求掉以得到实空间更大尺度上的正则配分函数。这样一次“粗粒化”的操作叫做对体系执行一次重整化群的变换。所以在这样的重整化群变换下,原始定义在N个单个自旋上的求和和连乘最终将变换到定义在N/2个集团上的求和和连乘的形式: 。现在将构成体系的N个自旋划分成N/2个互不相交的集团,每个集团内部有2个自旋。相邻集团间有相互作用。将每个集团内部的第二个自旋的自由度求和求掉以得到实空间更大尺度上的正则配分函数。这样一次“粗粒化”的操作叫做对体系执行一次重整化群的变换。所以在这样的重整化群变换下,原始定义在N个单个自旋上的求和和连乘最终将变换到定义在N/2个集团上的求和和连乘的形式:

因为相变临界点处关联长度发散,体系呈现出自相似性(即标度不变性)。所以我们要求重整化群变换后的配分函数和变换前具有完全相同的数学形式(即重整化群保持体系配分函数的形式不变):
 
上述变量恒等式对任意的  的组合都要成立。所以: 的组合都要成立。所以:

上述四个式子即是控制体系耦合常数跑动的重整化群方程!容易解得:

注意上述三个方程定义了在一次重整化群变换下体系耦合常数的变动。当我们对体系进行多次重整化群变换的操作后,上述方程其实可以看成是一组相互耦合的非线性迭代方程。相变临界点对应于该方程的不动点,因为当方程迭代收敛到不动点时,当继续积分掉小尺度的内禀自由度从而把体系扩大到更大的空间尺度时,体系的耦合常数将不再发生变动。也就是说,此时整个体系达到了不同空间尺度上完全的自相似性,而这种完全的自相似性恰好对应相变的临界点!对于某些特殊情况,如果在反复进行重整化群的操作后,控制体系相互作用的耦合常数最终跑到(趋向于)0,这就意味着在更大的空间尺度上看整个体系其实本质上是不存在相互作用的!也就是说,虽然体系存在小尺度自由度上的局域相互作用,但如果从更大的空间尺度上来看,整个体系其实本质上和理想气体体系没有区别!而一个理想气体体系永远都处于气相这一单一相,没有任何相变过程的发生。所以原相互作用体系不存在相变。
对于我们现在研究的一维Ising模型,相互作用J隐藏在耦合常数 里。为了研究J在重整化群作用下的跑动和不动点,我们只需要关注第一个关于 的迭代方程。又因为现在只考虑自发磁化问题,所以外场B=0,对应耦合常数 。将该方程可以化简成:

分别作出方程左边和右边的函数图像:

容易发现对于任何  落在蓝线上作为初始位置的点,经过反复执行上述迭代方程,最终对应的轨迹将是一条不断在蓝线和红线间来回反弹的往左下方跑的折线锯齿形路径。且随着重整化群的操作一次次地执行下去,该路径会逐渐跑向并收敛到坐标原点,此时对应到耦合常数 落在蓝线上作为初始位置的点,经过反复执行上述迭代方程,最终对应的轨迹将是一条不断在蓝线和红线间来回反弹的往左下方跑的折线锯齿形路径。且随着重整化群的操作一次次地执行下去,该路径会逐渐跑向并收敛到坐标原点,此时对应到耦合常数  。 。
同时注意到关于 K2的不动点方程  除了有一个 除了有一个  的解,还有一个 的解,还有一个  的平凡解。所以在执行了无穷多次的重整化群操作后,体系的不动点将出现在 的平凡解。所以在执行了无穷多次的重整化群操作后,体系的不动点将出现在 或 或 或 或  的地方!所以在有限温下,当该体系经历了无穷次重整化群操作后,体系的相互作用常数逐渐趋向于0!所以根据前面的分析可知:一维Ising模型在有限温下无相变!这一结论进一步检验了先前第一节中通过严格求解正则配分函数导出的结论的正确性以及第三节中使用平均场近似求解的缺陷。更加值得注意的是,这里从一维Ising模型求解中引入的重整化群的思想不仅在统计力学,更在现代理论物理的诸多分支(比如量子场论)中占据着极其重要的地位! 的地方!所以在有限温下,当该体系经历了无穷次重整化群操作后,体系的相互作用常数逐渐趋向于0!所以根据前面的分析可知:一维Ising模型在有限温下无相变!这一结论进一步检验了先前第一节中通过严格求解正则配分函数导出的结论的正确性以及第三节中使用平均场近似求解的缺陷。更加值得注意的是,这里从一维Ising模型求解中引入的重整化群的思想不仅在统计力学,更在现代理论物理的诸多分支(比如量子场论)中占据着极其重要的地位!
本文转载自公众号:中国科学院理论物理研究所 | 


























