本帖最后由 Jack小新 于 2025-1-21 15:16 编辑

一.算法简介
1.算法提出
模拟退火算法(Simulated Annealing,SA)最早的思想是由N. Metropolis 等人于1953年提出。
Nicolas Metropolis于1915年6月11日出生在美国芝加哥。Metropolis在芝加哥大学获得理学学士(1936年)和化学物理学博士(1941年)。在他读博士期间,他和罗伯特·穆肯一起工作。毕业后,他在芝加哥大学任讲师,师从詹姆斯·弗兰克。不久之后的1943年,罗伯特·奥本海默(Robert Oppenheimer)将他从芝加哥招募到曼哈顿计划,他在哈罗德·c·尤里(Harold C. Urey)的团队工作。后来,他加入了芝加哥大学冶金实验室,在爱德华·泰勒的指导下工作,泰勒鼓励他进入理论物理领域。在洛斯阿拉莫斯,Metropolis与理查德·费曼(Richard Feynman)一起研究“用于手动计算的机电设备”。
1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。模拟退火算法参考了固体物质的退火过程,从一个初始温度开始,以一定的速率降温。伴随着温度不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。

图1 Nicholas Metropolis
2.算法优点
(1)算法简便,代码实现较为容易。
利用SA算法解决一个较为复杂的问题时,我们仅需要设置一个初始温度,并随着温度降低更新最优解。当迭代次数足够大或者最优解满足一定要求时,我们便结束求解。
(2)易于跳出局部极小点
在求解过程中,我们会根据随机产生的概率去接受新解。如果此时最优解处于一个局部极小点,我们通过这个机制便有可能跳出该局部极小点。
(3)稳定性和可靠性高
在解决TSP问题时,发现SA算法求解效果较为理想。当迭代次数到达一定程度时,计算的最优解非常稳定。
3.算法适用场景
SA是一种用于全局优化问题的随机搜索算法。它在许多实际的优化问题中都有广泛的应用,特别是一些具有复杂搜索空间和多个局部最优解的场景。
在复杂的组合优化问题、函数优化、高维优化问题、求解NP难问题和具有噪声或不确定性的优化问题上,SA算法可以较为高效地进行解决。具体来说,SA算法可以有效得应用于解决旅行商问题(TSP)、作业调度问题、装箱问题(Bin Packing Problem)、车辆路径问题(VRP)、网络设计问题、图像处理中的滤波和匹配、资源分配与分配问题、神经网络训练中的权重优化、分子结构优化和组合电路设计和布局问题。由此可见SA算法的强大!
二.物理退火过程
1.退火
退火是指对物体加温再冷却的过程。将固体加热到足够高的温度,使分子呈随机排列状态,然后逐步降温使之冷却,最后分子以低能状态排列,固体达到某种稳定状态。
2.退火过程
(1)加热过程
增强粒子的热运动,消除系统原先可能存在的非均匀态。
(2)等温过程
对于环境换热而温度不变的封闭系统,系统状态的自发变化总是朝自由能减少的方向进行,当自由能达到最小时,系统达到平衡状态。
(3)冷却过程
使粒子热运动减弱并渐趋有序,系统能量逐渐下降,从而得到低能的晶体结构。
三.算法思想
1.总体思想
SA算法首先在解空间中随机选择一个点作为起始点(当前最优解)并计算其适应度函数。根据该点产生一个邻解,并与当前最优解进行比较。若邻解计算的适应度函数更小,则更新当前最优解。否则,以一定的概率去接受该邻解。如此迭代达到目标次数后,当前状态便是我们能够接受的最优解。

图2 求解过程图示
2.Metropolis准则
在温度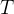 时,由当前状态 时,由当前状态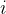 到新状态 到新状态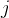 。若 。若 ,则接受 ,则接受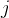 作为新状态。否则,计算概率 作为新状态。否则,计算概率 ,若 ,若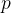 大于 大于 之间的一个随机数,则仍然接受状态 之间的一个随机数,则仍然接受状态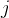 作为当前最优解。否则保留状态 作为当前最优解。否则保留状态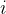 。其中 。其中 可以调整整体接受程度。当 可以调整整体接受程度。当 越大,接受程度越高。(一般可以把 越大,接受程度越高。(一般可以把 设置为1)。 设置为1)。

四.案例分析(SA解决TSP问题)
1.题目要求
求解中国34个一线城市的最优路线
以下表格给出中国34个一线城市的经纬度坐标。

2.求解过程
(1)设置相关参数
执行循环迭代程序之前,需要设置好相关参数。例如初始温度、降温速度、最大迭代次数。为了得到一个更精确的最优解,在这些基础的参数之上,添加了其他的参数。通过对这些参数进行组合,可以获得不同的求解模式,进而可以比较不同方法之间的差异,同时也体现了“优化”的思想。
%% Initial parameters of ACO
T0=1; % Initial Temp.%1
T=T0;
alphaa=0.99; % Cooling factor0.99
maxIteration = 800;%%800
chooseNeighbour = 2;%产生邻解选择:1-调换两个位置;2-逆序;3-插入
interloop = 1;%是否进行内循环标志(一个T下多次取邻解):0-不进行内循环;1-进行内循环
interloopcount = 5;%一个T下多次取邻解的次数
ifCheckRoute = 1;%是否检查路线标志:0-不检查;1-检查
RunCount = 0; %实际运算次数(实际产生了多少个不重复新路线)
t_Repeat = zeros(1,1); %路线重复时t的值
chooseNeighbour:选择产生邻解的方式,共有调换两个位置、逆序、插入三种方法。
Interloop:是否进行内循环标志(一个T下多次取邻解)
Interloopcount:一个T下多次取邻解的次数。
ifCheckRoute:是否检查路线标志。
(2)生成初始解并计算适应度函数
%% Problem preparation
% Create the graph
graphNo = 1;
[ graph ] = createGraph(6);
nVar = graph.n;
A.position = randperm(nVar);
A.cost = fitnessFunction ( [A.position, A.position(1)] , graph);
(3)生成邻解
在生成邻解的方式当中,最简单的是随机交换两个位置。通过randsample()函数在城市序号当中任意挑选出两个位置,并将对应的序号交换。但是该方法对原路径的变动不大。因此我们使用了逆序和插入的方法对代码进行了优化。
%方法1 随机交换两个城市的顺序
function [B] = createNeighbour(A)
index=randsample(length(A),2);
i=index(1);
j=index(2);
B = A;
B(i) = A(j);
B(j) = A(i);
end
%方法2 逆序
function [B] = createNeighbour1(A)
index=randperm(length(A),2);
i=index(1);
j=index(2);
B = A;
if i<j
for n = i:j
B(n) = A(i+j-n);
end
else
for n = j:i
B(n) = A(i+j-n);
end
end
end
%方法3 插入
function [B] = createNeighbour2(A)
index=randsample(length(A),2);
i=index(1);
j=index(2);
if i < j
B = [A(1:i-1),A(i+1:j),A(i),A(j+1:end)];
else
B = [A(1:j-1),A(j+1:i),A(j),A(i+1:end)];
end
% B(i) = A(j);
%
% B(j) = A(i);
end
(4)计算适应度函数
适应度是衡量一个解优劣的标准。在TSP问题中适应度则是路线的长度。该问题给出的是中国34个一线城市的经纬度坐标,我们不能简单的用两点之间的距离来进行求解。通过查找资料后,选择使用haversine公式进行计算。haversine公式基于地球表面上的大圆距离的定义,即通过球心的两点之间的最短距离。它利用了三角函数和对数函数来计算两点之间的距离,并考虑了地球表面上的曲率和地形等因素。

图3 haversine公式
将以上公式转换为代码,如下所示:
lat1 = y1;
lon1 = x1;
lat2 = y2;
lon2 = x2;
lat1Rad = deg2rad(lat1);
lon1Rad = deg2rad(lon1);
lat2Rad = deg2rad(lat2);
lon2Rad = deg2rad(lon2);
dLat = lat2Rad - lat1Rad;
dLon = lon2Rad - lon1Rad;
a = sin(dLat / 2) .^ 2 + cos(lat1Rad) .* cos(lat2Rad) .* sin(dLon / 2) .^ 2;
c = 2 * atan2(sqrt(a), sqrt(1 - a));
graph.edges(i,j) = 6371 * c; % 返回单位为千米的距离
在程序的初始部分,我们已经建立了一个L*L的矩阵,并将计算的任意两个城市之间的距离放入其中,方便后续适应度计算。
计算适应度依据城市的排序,取出相应距离再求和。因为SA算法用于最大值求解,所以在此我们将距离之和取负。
function [ fitness ] = fitnessFunction ( tour , graph)
fitness = 0;
for i = 1 : length(tour) -1
currentNode = tour(i);
nextNode = tour(i+1);
fitness = fitness + graph.edges( currentNode , nextNode );
end
fitness = -fitness; % SA is for maximization so multiple my -1 to change
% the minimization problem to a maximization problem
end
(5)判断是否接受新路线
如果新的路线比当前的路线长度更短,我们便直接将当前路径进行更新。如果新的路线比当前的路线长度长,我们便以Metropolis准则进行判断。在此,记录了接受劣路线的次数,方便后续进行分析。
if Delta < 0 % uphill move (good move)
A.cost = B.cost;
A.position = B.position;
Better_Route_Count = Better_Route_Count + 1;
else % downhill move (bad move)
Worse_Route_Count = Worse_Route_Count + 1;
P=exp(-Delta/T);
if rand<=P
A.cost = B.cost;
A.position = B.position;
Recept_Worse_Route_Count = Recept_Worse_Route_Count + 1;
else
Refulse_Worse_Route_Count = Refulse_Worse_Route_Count + 1;
end
end
(6)检查路线,避免迂回搜索
当迭代次数较大时,很容易产生重复解,为了提高效率,我们保存了历史路线并设置检查路线机制。一旦检测到路线重复时,程序便跳出本次循环进入下一次循环。特别的,我还记录了重复路线次数,用于比较程序的性能。
if ifCheckRoute == 1
[Check,lastroutes] = CheckRoute ( lastroutes , B.position);
if Check == 1
t_Repeat = cat(2,t_Repeat,t);
continue;
end
end
3.结果分析
(1)数据记录
根据不同组合进行了多次求解,数据记录如下。

图4 数据表格1

图5 数据表格2
(2)求解图像



(3)数据可视化
使用SA算法求出最优解之后,便可以做可视化处理。在中华人民共和国中央人民政府网站找到最新的中华人民共和国版图,该地图维护国家统一,捍卫国家领土主权。将中国地图做灰度处理之后,找到34个一线城市,根据SA算法求出的结果,绘制路线。

图6 数据可视化
————————————————
本文转载自CSDN博主:涵娃子
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/yzhh1124/article/details/141497263 | 


























