本帖最后由 graphite 于 2025-2-28 14:20 编辑
分支定界算法 (Branch and Bound) 作为求解一般的混合整数线性规划中最常见,最有效的方法,受到学界业界广泛的关注。目前主流的优化求解器均采用分支定界算法的框架来求解混合整数线性规划问题。
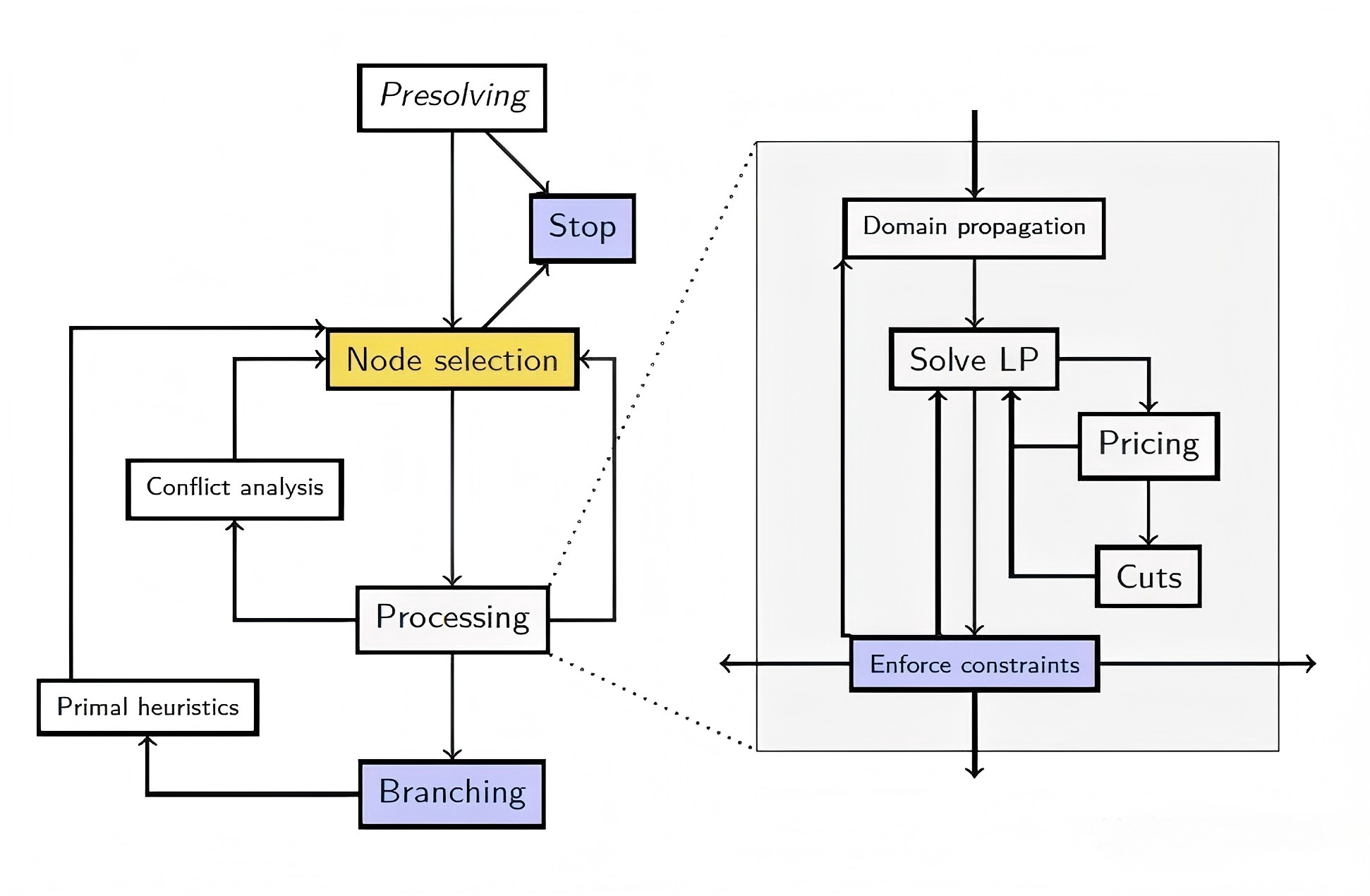
分支定界算法由几个关键模块:
表1 分支定界算法关键模块
1. 预求解 (Presolving) |
在算法启动前对原问题进行简化,消除冗余约束、固定变量取值、缩小变量范围,降低问题维度
|
移除固定变量(Fixed variable elimination) 、系数紧缩(Coefficient tightening)、约束冗余性检测(Redundancy checking)
|
2. 分支 (Branching) |
选择非整数变量进行解空间划分,生成子节点以缩小搜索范围
|
强分支(Strong branching) 、伪成本分支(Pseudocost branching)、可靠性分支(Reliability branching)
|
3. 节点选择 (Node selection) |
从活结点表中选择下一个待处理的节点,平衡搜索深度与广度
|
最佳界限优先(Best Bound First)、深度优先(Depth-First)、混合策略(Hybrid strategy)
|
4. LP求解 |
求解节点对应的线性规划松弛问题,提供下界估计与分支依据
|
对偶单纯形法(Dual simplex)、内点法(Interior-Point)、热启动(Warm start)技术
|
5. 割平面 (Cuts) |
在节点处理过程中添加有效不等式,收紧松弛问题的可行域
|
Gomory割平面(Gomory cuts)、 覆盖割平面(Cover cuts)、混合整数取整割(MIR cuts)
|
6. 原始启发式 (Primal heuristics) |
在搜索过程中主动寻找可行解,快速更新全局上界以加速剪枝
|
可行性泵(Feasibility pump)、 邻域搜索(Local search)、松弛解圆整(Rounding heuristics)
|
以上模块均在上图中有所体现,正是他们构成了优化求解器中基于分支定界算法的求解框架。
1 如何评价分支的好坏
考虑如下的混合整数线性规划问题:

我们在使用分支定界算法求解上述问题的过程中,得到其线性规划松弛问题的最优解为 x,这个x中如果存在非整数值的话,就需要对那些非整数值的变量进行分支。根据如上定义,我们给出预备分支变量的集合:

那么分支要做的事情就是在集合F中选择一个合适的变量来进行分支操作。显然选择哪个变量进行分支对整个分支定界算法有着非常大的影响。一般在优化求解器中我们会定义出一个打分函数来确定出到底应该选择哪个变量进行分支,那么这个打分函数可以用来评价每个预备分支变量的好坏,打分高的变量就表示采用该变量分支的话就对整个分支定界算法效果好,反之亦然。打分函数的定义如下所示:

其中cQ表示当前问题的目标函数,cQj-, cQj+分别表示如果用变量 j做分支的话形成的两个子问题的目标函数。那么上式中Δj-,Δj+就表示采用变量 j分支之后左右两个子问题目标函数相对于当前问题的增加程度。
我们知道Δj-,Δj+大于等于0,这是因为子问题是在更小的可行域上求极小值,所以子问题的目标函数值只会比当前问题的目标函数更小。我们在分支定界的搜索过程中总是希望得到的松弛问题的目标函数值越大越好,因为这就表明下界是越大的,这对于加速我们整个分支定界算法显然有着很大的帮助。由此可得Δj-,Δj+两个值越大就表明分支的效果越好。这就是为何我们定义出上式形式的打分函数来评价分支。
进一步,我们给出改进版本的打分函数:

改进版本和原始版本的差距增加了一个参数є,一般我们设定є=10-6,主要是为了防止出现0打分的情况。基于以上打分函数,我们就可以对每一个预备变量进行打分,选出打分最高的进行分支即可。
2 分支策略
分支的策略有很多,其基本思想就是采用打分函数来对分支的好坏进行评价,我们这里介绍以下四种分支策略。
2.1 Strong Branching
让我们回顾一下改进版打分函数:

其关键问题在于获得Δj-,Δj+。一个简单粗暴的想法就是我们通过直接求解每一个分支变量做分支后的的2个线性松弛子问题,即可获得 。数值实验表明 Strong Branching 可以有效提升下降的改进,但是显然 Strong Branching 的计算代价太大了,每做一次分支需要求解2|F|次线性规划,这显然是很难接受的。
2.2 Pseduocost Branching
Strong Branching 确实有利于提升下降,但是计算代价太大,这主要是由于我们需要求解很多的线性规划问题来估计分支变量后的效果。我们就会思考是否可以在整个 Branch and Bound 搜索过程中来对目标函数的改进进行估计,这样就无需真的求解线性规划去估计对于下降的提升,那么这种方法就是 Pseduocost Branching 方法。

μj-和μj+ 的含义为分支选择xj变量后单位xj引起的下界提升。当然在整个 Branch and Bound 搜索过程中,我们可能会不止一次对同一变量进行分支,我们就记录下这些分支的历史进行,用历史信息的均值去估计下降的提升,由此可得如下表达式:

上式中M表示在当前 Branch and Bound 搜索过程中,我们对变量j 曾经分支过M次,那么上式右端项分子就是把历史上这 次分支引起的下界提升值求和。整个表达式就表示我们用历史上对该变量进行分支后的下界提升的均值来估计在当前节点对该变量进行分支后下界的提升。之后借用打分函数即可评估每个分支的好坏:

Pseduocost Branching 方法巧妙的利用了历史信息来对下界提升进行了估计,和 Strong Branching 相比它无需求解线性规划,其计算效率会很高。Pseduocost Branching 的缺点在于比较依赖于历史信息,在有充分多的历史样本的情况下,我们用历史的均值来估计才会比较准确。但是在 Branch and Bound 搜索的初期显然我们并没有多少历史信息来做估计,这就有可能会导致 Pseduocost Branching 算法效果变差。
2.3 Hybrid Branching
前面介绍了 Strong branching 和 Pseduocost Branching, 这两种方法各有各自的优势,也各自有各自的缺点。Hybrid Branching 的思想也很简单 就是将上述两种分支方法结合,以达到却长补短的效果。我们知道 Pseduocost Branching 在搜索初期可能由于没有多少历史信息来做估计而导致算法效果变差,那么我们就考虑在 Branch and Bound 搜索初期先采用 Strong Branching 的方法,然后当搜索树的深度达到一定深度之后,再切换到 Pseduocost Branching,这就是 Hybrid Branching 的一种实现版本。
这样做的好处就是 在搜索初期 我们可以用准确性高的 Strong Branching 来收集足够的历史信息,当有了足够的历史信息后我们再启动 Pseduocost Branching,这样就可以保证 Pseduocost Branching 的准确性,同时又可以有效地降低计算量。当然 Hybrid Branching 的版本不止这一种,还会有其它的结合方式,但基本思想都逃脱不出这个框架。
2.4 Most Infeasible Branching
最后我们介绍一种非常简单的分支策略。如果说一个非整数变量的取值非常接近于0.5,那我们感觉这类非整数变量是距离整数点比较远的变量,对于整数约束来说这些变量就是 Most Infeasible 的,我们自然而然会想到首先把这些变量进行分支。基于此思想,我们给出打分函数的表达式:
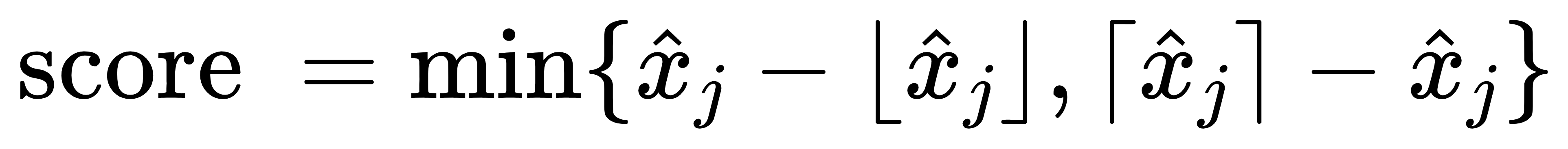
实际的数值实验结果表明 Most Infeasible Branching 这类分支策略并没有明显优于随机选择的分支策略,因此该分支策略并不是一种非常有效的分支策略。
参考文献
[1] Achterberg T. Constraint integer programming[J]. 2007.
[2]Bestuzheva K, Besançon M, Chen W K, et al. The SCIP optimization suite 8.0[J]. arXiv preprint arXiv:2112.08872, 2021.
本文转载自公众号“科研式学习” 2023年08月28日
| 


























