增广拉格朗日乘子(Augmented Lagrangian multiplier)方法是一种用于求解带有等式和不等式约束的优化问题的技术。它结合了拉格朗日乘数法与罚函数的思想,是解决约束优化问题的一种有效工具。
在标准的拉格朗日乘数法中,我们构造拉格朗日函数:

这里f(x)是目标函数,gi(x)是等式约束条件,λi是对应的拉格朗日乘数。然后通过求解这个函数相对于x和λ的极值来找到原问题的解。然而,在实际应用中,直接使用拉格朗日乘数法可能会遇到一些困难,比如需要初始猜测的拉格朗日乘数,以及可能存在的鞍点问题。为了解决这些问题,引入了增广拉格朗日乘子方法。增广拉格朗日函数的形式如下:
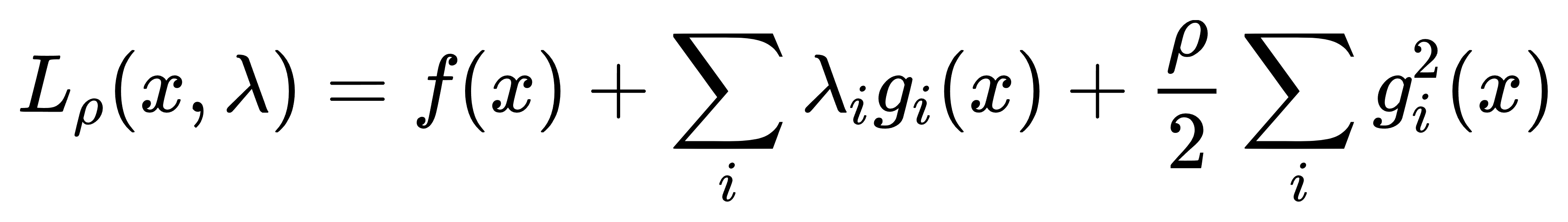
这里增加了最后一项惩罚项,其中ρ> 0是一个罚参数。这一项可以看作是对违反约束的惩罚,当约束被违反时,该惩罚项会增大,从而使得整体的目标函数值增大。随着迭代过程的进行,可以通过调整ρ和更新λ来逐步逼近最优解。增广拉格朗日乘子方法的优点在于它可以更好地处理非线性约束,并且具有更好的数值稳定性。此外,它还允许在每次迭代中使用更宽松的停止准则,因为即使约束没有严格满足,额外的惩罚项也会促使后续迭代中的解更加接近可行区域。
增广拉格朗日乘子(ALM, Augmented Lagrangian Method)方法的实现方式通常遵循一个迭代过程,该过程包括更新优化变量、拉格朗日乘数和罚参数。以下是几种常见的实现方式:
1. 标准增广拉格朗日算法
这是最基础的实现方式,包含以下步骤:
- 初始化:设置初始拉格朗日乘数λ0和罚参数ρ> 0。
- 迭代:
- 对于每一个迭代步k,求解下列问题以更新优化变量xk+1:
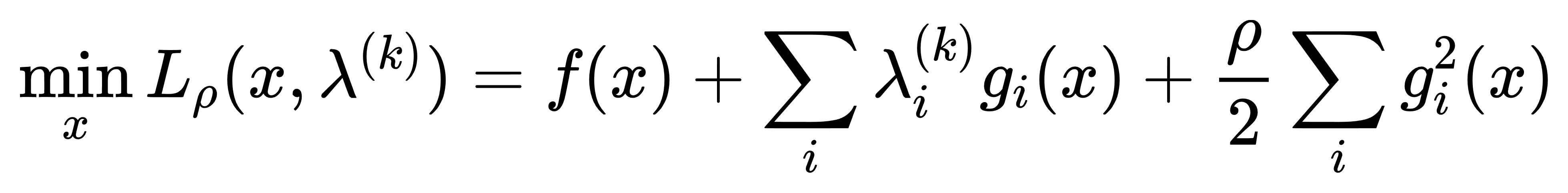
- 更新拉格朗日乘数:
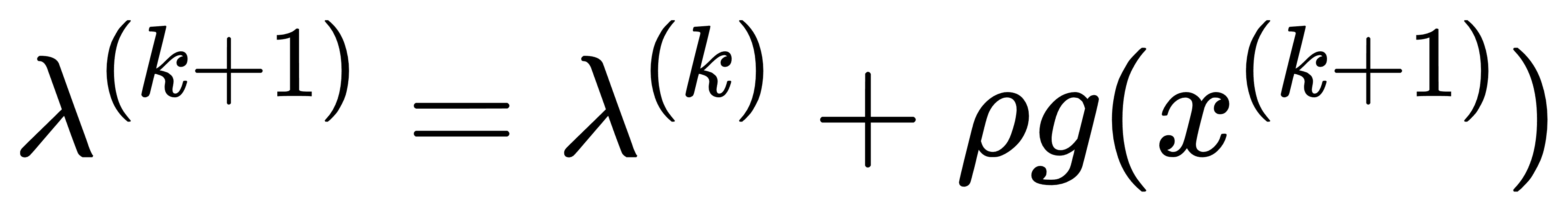
- 如果必要,调整罚参数ρ。
- 停止准则:当满足某个收敛条件时停止迭代,例如约束违反量足够小或目标函数的变化量小于给定阈值。
2. ALM结合内点法
这种方法融合了增广拉格朗日法(ALM)与内点法的优势,专门用于求解带不等式约束的优化问题。其基本思路是:
首先对所有不等式约束 gi(x)≤0 引入松弛变量 si≥0,将其转化为等式约束 gi(x)+si=0。
然后在原始目标函数中附加增广拉格朗日项和对数障碍项,即
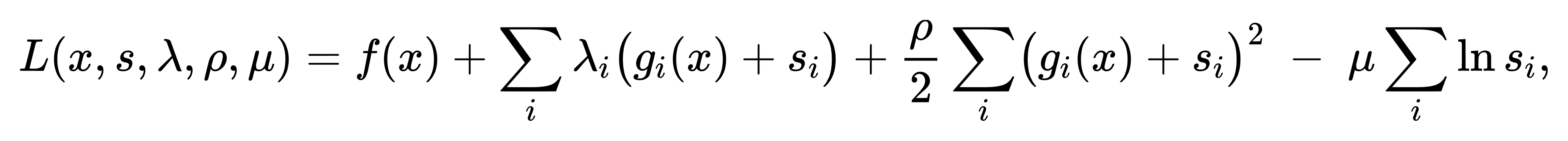
其中 ρ>0为罚参数,μ>0为障碍参数。
在每一次迭代中,首先固定 λ,ρ,μ 求解一个等式约束的子问题(可借助牛顿法或拟牛顿法),以获得x和s;然后更新拉格朗日乘子 λi←λi+ρ (gi(x)+si),并适当减小μ保证可行性。一方面利用 ALM 的全局收敛性来处理等式约束与惩罚,另一方面借助对数障碍保持si>0使解始终留在不等式可行域内部,从而兼具稳定性与高效性。
3. 并行化和分布式实现
对于维度极高或样本量巨大的优化问题,可在 ALM 框架下引入并行与分布式计算:
分区:将数据与决策变量按块划分,针对每个子块独立构造局部增广拉格朗日函数。
任务分配:不同计算节点(或线程)并行求解各自的子问题,然后通过通信协议(如 MPI、Parameter Server)交换拉格朗日乘子或公共变量的更新信息。
同步机制:可采用同步更新(Barrier 同步)保证全局一致性,也可使用异步更新来进一步提高硬件利用率,容忍少量延迟或“陈旧”的拉格朗日乘子信息。能显著降低单节点计算与内存压力,并在多核或多机环境中实现接近线性的加速比。
4. 随机增广拉格朗日方法
在机器学习领域,特别是处理大数据集时,随机增广拉格朗日方法是一种有效的变体。它每次只用一部分数据(即“迷你批次”)来更新模型参数,从而减少了每一步所需的计算量。这对于在线学习和实时应用尤其有用。
每次仅选取一小批样本(mini-batch)来构造近似增广拉格朗日函数:
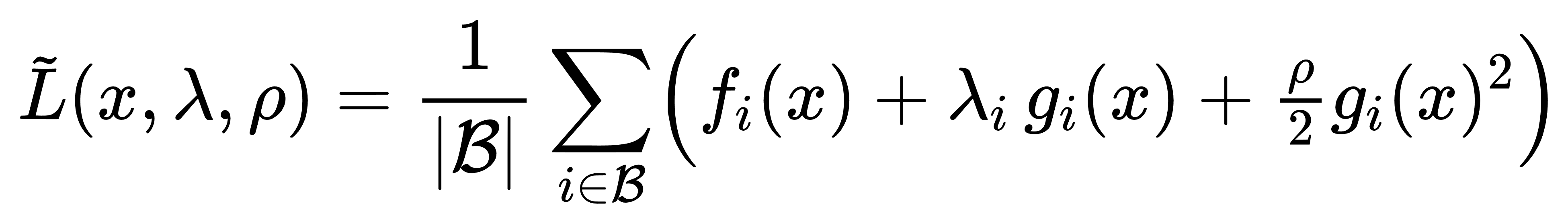
从而以随机梯度或随机牛顿步更新 x 和 λ。 随机方法可用于在线学习——当新数据到来时,继续对已有乘子和罚参数进行增量式更新,而无需重新遍历全量数据。 收敛性可通过控制步长衰减和加大罚参数 ρ 来保证,实验证明在大数据场景下仍能可靠收敛。
5. 自适应增广拉格朗日方法
这种变体允许动态调整罚参数ρ,以提高收敛速度或改善数值稳定性。自适应策略可以根据当前迭代状态自动选择合适的ρ值。
在每次迭代后,根据约束残差 ∥g(x)∥的大小自动增大或减小 ρ。例如,当残差未能有效下降时,可将 ρ 按比例放大,以加强对约束违例的惩罚;反之则适度放松。
也可结合乘子变化量 ∥λk+1−λk∥ 作为调整依据,以平衡乘子更新的震荡性。
自适应策略通常能显著加快达到高精度解的收敛速度,并避免因 ρ\rhoρ 过大导致的数值病态。
实现注意事项
在实现增广拉格朗日法(ALM)及其各类变体时,需要关注以下几点以确保算法既高效又稳健。
首先,合理初始化拉格朗日乘子 λ和罚参数 ρ 至关重要:过小的 ρ 会导致约束满足缓慢,过大的 ρ 则可能引起数值病态或收敛震荡;因此通常建议从中等规模开始,并在预热阶段监测残差变化。其次,罚参数的更新规则应当结合约束违例和乘子增量来动态调整:当残差下降乏力时适当增大 ρ 以加大惩罚,反之可稍作放松;也可引入启发式或自适应策略,以平衡收敛速度与算法稳定性。再次,设计多重停止条件,不仅监测原始目标与约束残差的双重收敛,还应纳入最大迭代次数、时间预算或计算资源限制,以便在工程实践中防止过度计算或超时。
此外,不同问题场景下的并行化、松弛变量引入或随机化小批次技术,会对实现细节产生不同要求——如同步通信的频率、对数障碍的退火速率、mini-batch 的大小等,都需根据问题规模和硬件环境进行调优,需结合问题特性、资源约束和精度目标,方能在理论保证与工程效率之间取得最佳平衡。 | 






















