本次讲座我们邀请到广西大学的高放教授,分享基于相干伊辛机在QUBO问题求解上的加速优势所发展的多阶段量子分解算法,该算法在模型构建、算法设计等层面进行创新,相比经典求解器可实现超 95%加速求解,且框架可迁移至类似结构的大规模混合整数问题。实验结果表明,相较于传统Gurobi和量子退火混合方法,该算法在求解时间上提升显著,且在目标函数值与可行性约束上保持甚至优于经典算法,验证了其在复杂电网调度中的量子计算优势与工程实用性。讲座回放及PPT原文链接请见本文最后部分。

1. 背景介绍
在智能电网中,机组组合(Unit Commitment,UC)承担着电力市场出清的核心职能:火电、水电以及可再生能源机组选取何时开机、出力多少,直接决定日内发电计划的可执行性与系统的安全裕度。随着电网规模由区域级扩展至跨省骨干网,并网主体由以火电为主转向“风‑光‑储”深度耦合,传统的 UC 问题被重新推上研究前台。新能源出力的不确定性使实时功率平衡的可行域急剧收缩,若调度策略缺乏前瞻性,弃风弃光和备用容量不足将同时出现,经济‑安全双目标遂难兼顾。更为严峻的是,火电装机占比已从 2022 年底的36%进一步下滑,而统调总容量持续攀升,迫使系统运维者通过更精细的发电侧优化来弥补惯性与调节能力的缺口。

从系统效益角度看,精确的机组组合不仅能够在保持 N‑1 安全准则的前提下降低边际发电成本,还可与风光预测‑消纳模型耦合,提高可再生能源上网比重并显著压缩碳排放。电力行业营业收入在 2017‑2023 年间近乎翻倍,需求激增的背后隐藏着更高昂的备用、燃料和碳成本——这些支出能否被有效抑制,取决于 UC 模型对多能协同的捕捉能力以及求解器对大规模混合整数问题的处理效率。
然而,UC 天生是高维、非线性的混合整数优化。每台机组的启停状态 Ui,t 为二进制变量,与连续功率 Pi,t 通过最小出力、爬坡限制及最小启停时间强耦合;系统中时序耦合约束的数量随“机组数 × 时间段”线性增长,使得问题维度在新能源渗透率提升后迅速膨胀。经验上,即便采用商业求解器,在百台机组、二十四时段的日计划规模下仍难以在实用时限内获得全局最优或强可行解,传统启发式或松弛‑修复方法则容易陷入局部最优或产生不可行调度。
2. 模型构建
2.1 传统机组组合
在数学层面,经典 UC 可以抽象为以下混合整数二次规划。设 NG 为机组集合,T 为调度时段集合,决策变量包括机组启停状态 Ui,t∈{0,1} 与出力 Pi,t∈R≥0。成本函数包括了二次发电成本和线性发电成本以及启停成本:
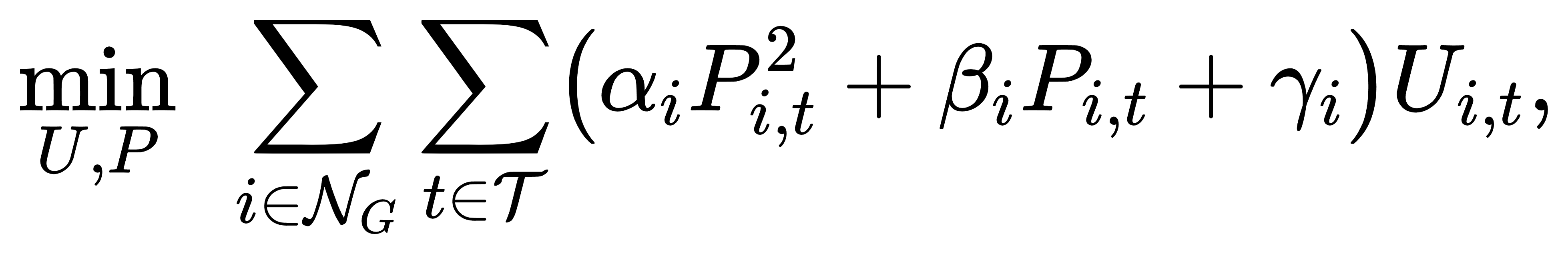
配合以下约束:
(1) 系统功率平衡:
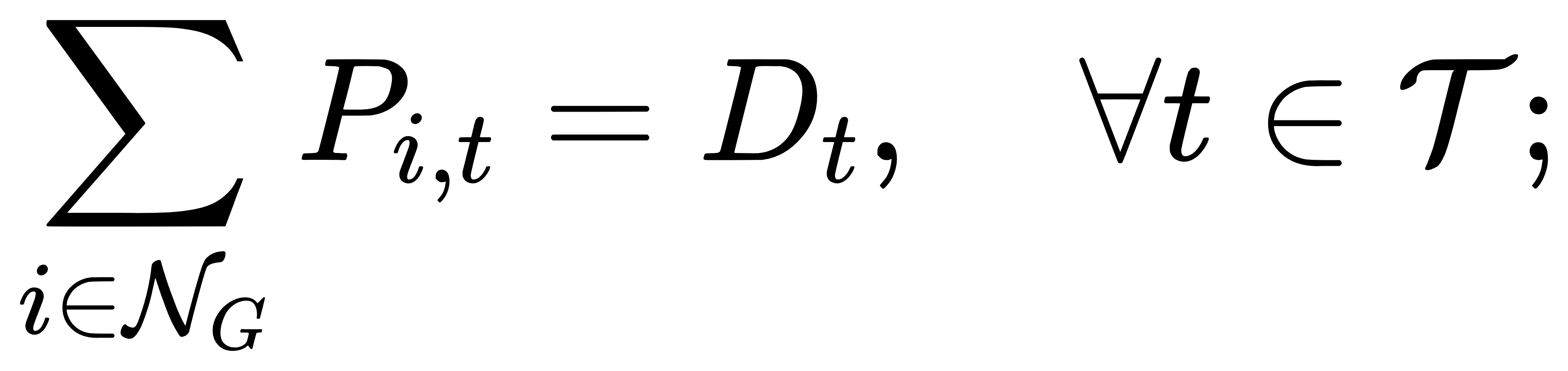
(2) 机组容量上下限:
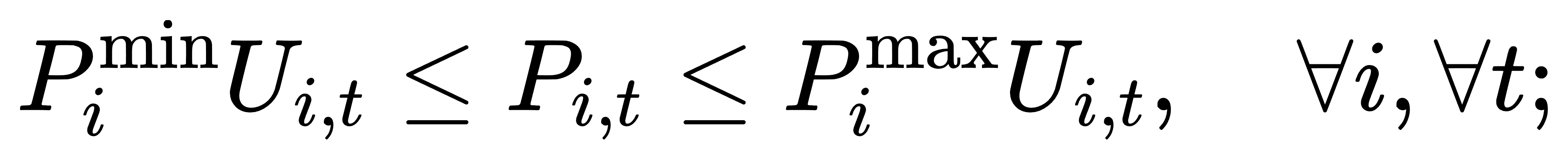
(3) 最小开停机时间:
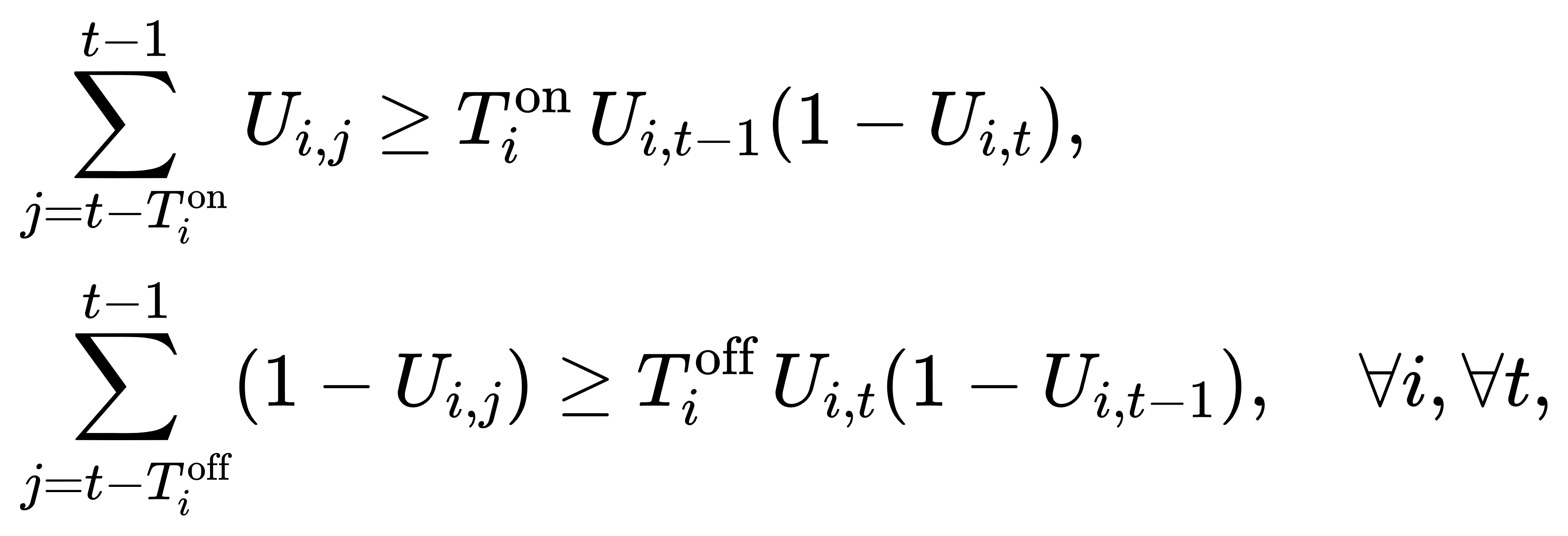
其中 Tion/off分别为机组 i 的最小连续开机与停机时长。
在实际实现中,模型还需叠加爬坡率、冷启成本、启停逻辑等附加约束,但即便是上述“简化”版本,已足以让整数搜索空间呈指数级增长。然而对于传统 UC算法, 当新能源功率预测误差通过储能‑火电联调被部分抵消后,搜索空间仍受二进制维度主导,导致求解时间大于调度滚动窗口。因此,引入传输线切换、储能协同与量子分解算法成为后续升级方向。
在发电侧优化的基础上,进一步提升系统经济性与安全性的关键在于拓扑结构的灵活调度,即最优传输线切换(Transmission Switching, TS)的引入。传统调度策略假定输电网络结构固定,而智能电网则提供了对网络拓扑进行动态调整的技术基础。由于电能无法大规模存储,任何节点的发电‑负荷不平衡需即时通过潮流转移予以缓解;而一旦部分线路负荷接近极限,就可能触发所谓的潮流阻塞(congestion)现象,诱发次优的发电调度,甚至推高全网发电成本。TS 的目的在于借助线路通断状态的灵活配置,实现潮流在时空维度上的再分布,以规避阻塞、释放冗余容量、增强系统弹性。
2.2 最优传输线切换
2.2.1 传统切换策略
传统 TS 策略通常在已定机组组合前提下进行,以辅助降低系统成本或强化 N‑1 安全性。我们先给出该情形下的典型模型。设 NL 为传输线集合,每条线路 l∈NL 对应二元通断变量 Zl∈{0,1} 与潮流变量 Pl∈R,此外 θn 表示节点 n 的电压相角,采用直流潮流近似下,其数学形式如下:
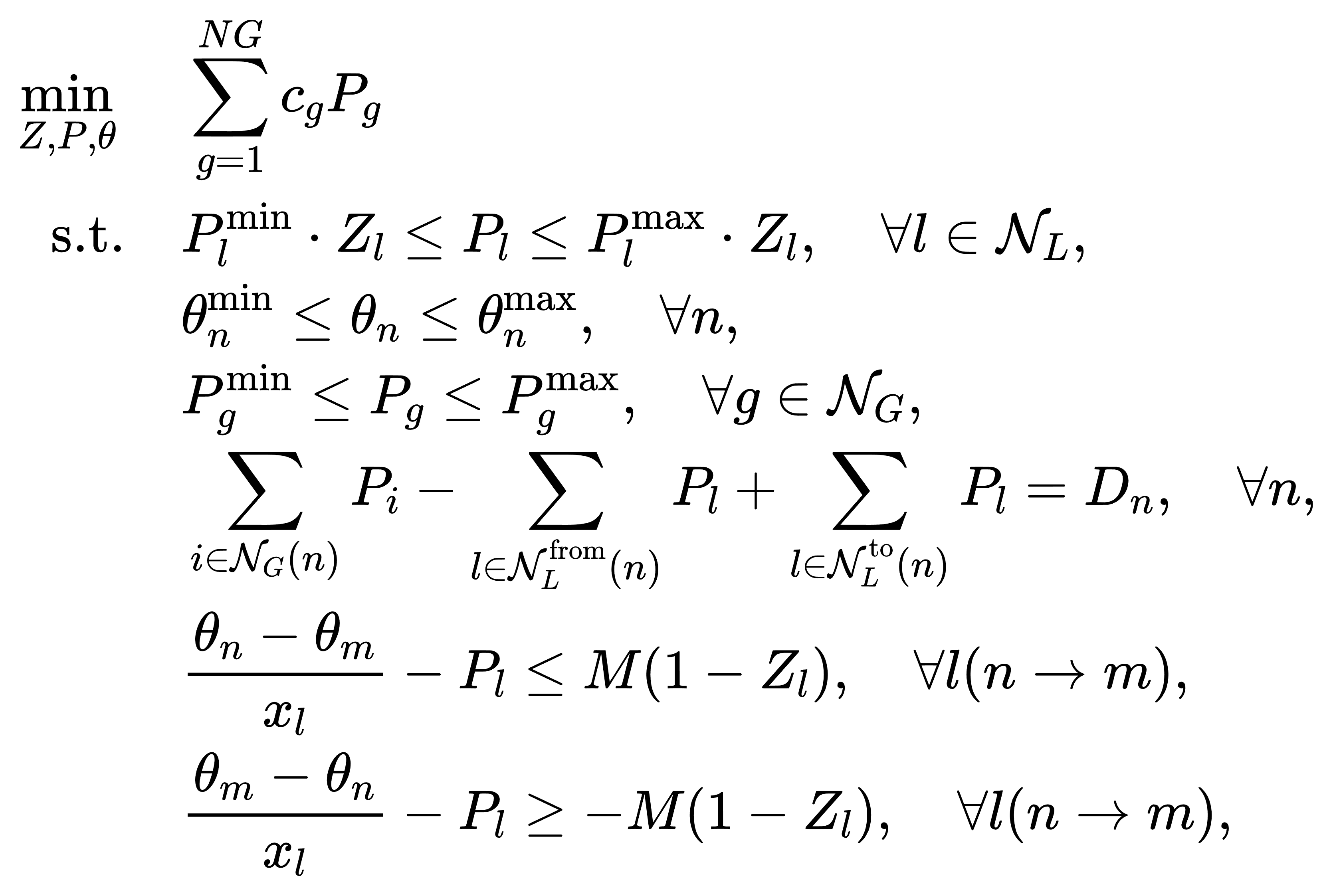
其中 xl 为线路电抗,M 为大常数,用于约束非激活线路使其对应潮流无效,起到“强制断开”的作用。节点功率平衡约束仍然成立,但在线路状态 Zl 为 0 时,潮流 Pl 被强行置零。
2.2.2 联合优化的UC-TS切换策略
传统模型的优势在于能够通过有限几条线路的状态调整产生显著的系统收益,但其不足亦显而易见:与机组组合脱耦建模难以捕捉两者间的非凸交互,尤其是在联合优化目标为系统总成本、碳排、备用约束等综合函数时。这种背景促使研究者进一步提出将 UC 与 TS 联合建模的策略,在单一模型框架中统一发电侧与网络侧的调度变量,从而发挥两者的协同优化潜力。

考虑联合优化下的 UC‑TS 模型,其目标函数可以表达为:
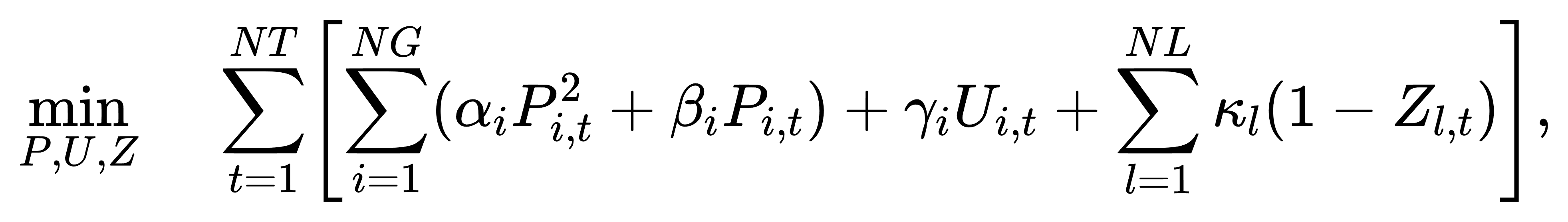
其中 κl 是传输线切换的惩罚成本,用于反映每次拓扑调整的经济代价与可能引入的运行风险。对应的约束体系包含如下内容:
(1) 节点功率平衡: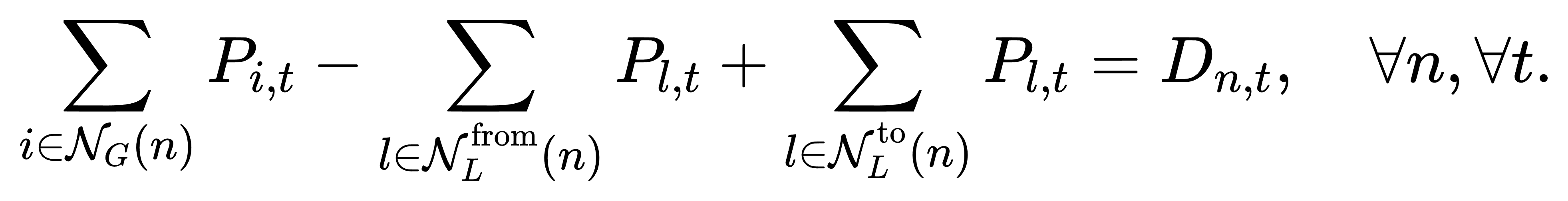
(2) 机组容量约束(考虑其他逻辑变量):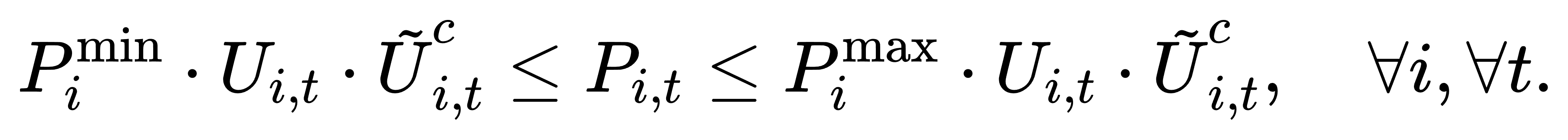
(3) 传输线容量限制: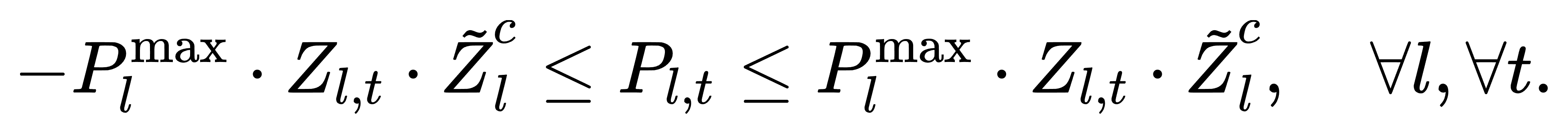
(4) 节点相角与潮流关系(直流潮流模型):
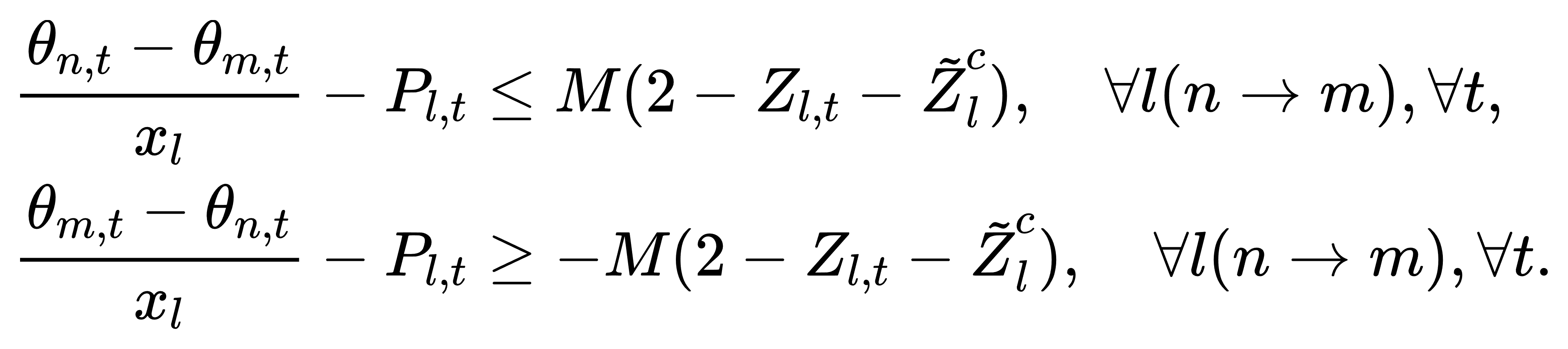
(5) 机组启停时间约束:
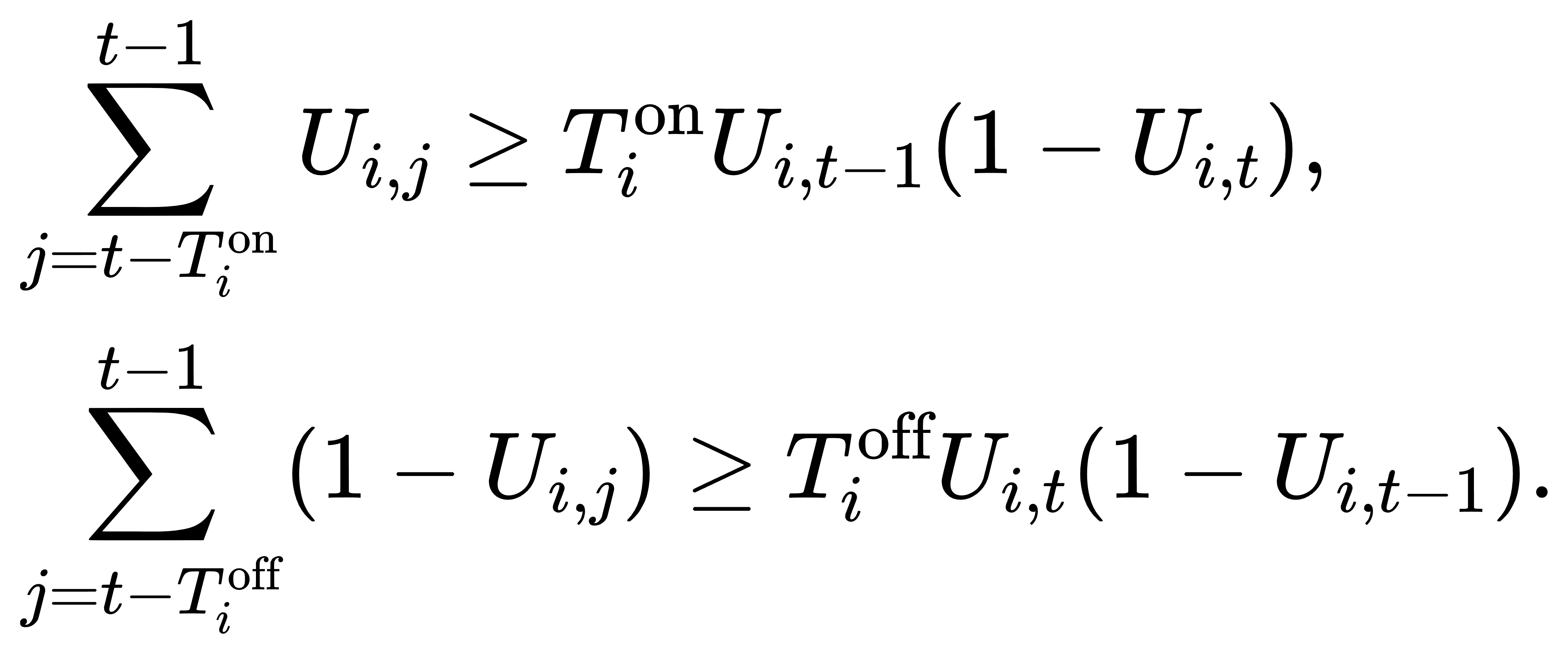
(6) 拓扑完整性与切换次数约束:
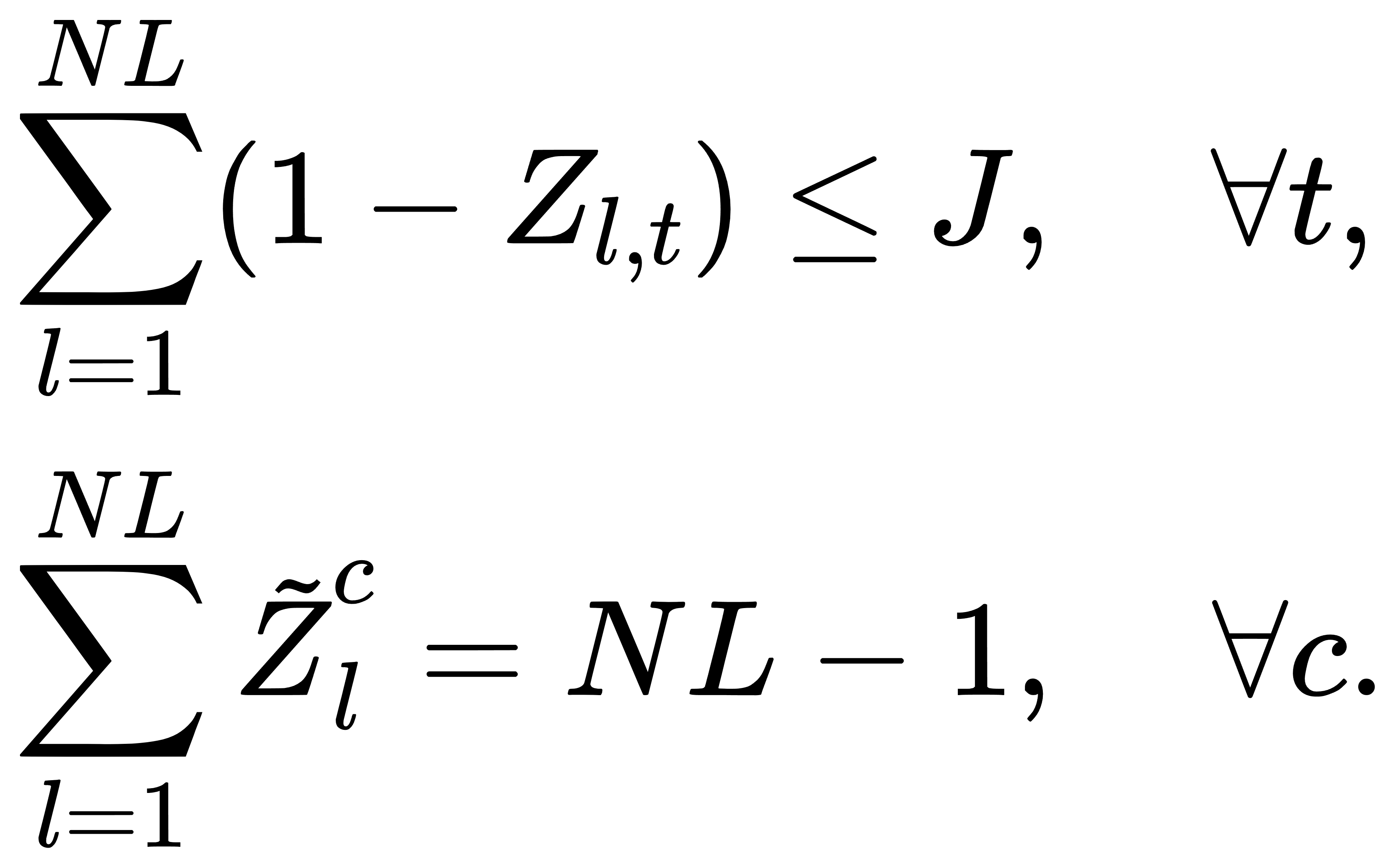
此模型较 UC 或 TS 单独建模显著提升了描述能力,同时也带来新的求解挑战——变量维度的指数增长,约束空间的稠密性,以及目标函数的非凸性与离散‑连续变量之间的复杂交互。例如本项目后面讲到的以IEEE-RTS-24总线为例的具体模型,其中包含1,440个二进制变量,2016个连续变量和 6,818 个约束。使用Gurobi 方法使得时间求解时间慢(58s)且随规模指数增加;同时,将此模型直接转为 QUBO 模型后,其规模当前量子设备也难以处理。
正是这些因素,推动本文进一步引入基于量子分解的求解框架,以破解 UC‑TS 联合模型的维度诅咒,并在下一部分中展开其哈密顿量构造、分布式子问题划分与求解策略的系统讨论。
3. 算法设计
3.1 模型求解思路概览
原始模型存在变量多、约束多的问题,导致过于复杂,且现有算法难以直接求解,效率较低。本项目计划将原问题分解为不同的模块,与整数变量有关的问题由相干光量子计算机处理,而与连续变量有关的问题则由其他方法处理,旨在发展考虑传输线切换的安全约束机组组合量子分解算法。具体求解思路如下:
算法层面 - 分解算法:基于松弛问题的构造和灵敏度分析开发高效的多阶段分解算法,QUBO主问题采用相干伊辛机加速求解。
模型层面 - 多模块模型:根据优化功能将原问题划分为多个模块,通过传递割平面哈密顿量实现信息交互,最终实现“分而治之”地求解。
算法层面 - 平均共识:每个节点根据共识独立且并行地求解共识约束的局部问题,模型规模降低,大幅提升联合优化问题的求解效率。
以此利用模块间不同决策的相互影响,以实现电网拓扑和机组调度的联合优化及智能纠错。最终,通过使用分解共识算法求解多模块模型,并使用数值方法验证相干光量子计算机相较于经典求解器Gurobi的优越性。

3.2 基于Benders割平面的灵敏度割平面分解算法
在面对变量维度极高、约束条件密集的混合整数非线性规划问题时,直接求解无论在经典计算还是量子计算体系中都显得极为困难,特别是当前量子硬件(如光量子伊辛机)比特资源有限,无法支持上千个二进制变量的联合优化。在此背景下,本文采用基于Benders割平面的灵敏度割平面分解方法,构建主从结构,将原问题拆解为多个结构性子问题与一个主问题,并在主问题层转化为QUBO形式交由量子设备处理,实现优化任务的分治求解。虽然该方法以传统Benders分解为基础,但针对强对偶性不成立的结构(如拓扑切换引起的约束变形),引入灵敏度替代与数值近似的处理策略,从而在理论框架上兼顾了精确性与可实现性。
我们从经典Benders算法的Lagrangian函数出发。给定原问题变量划分为二进制主变量 y 与连续从变量 x,其Lagrangian如下:
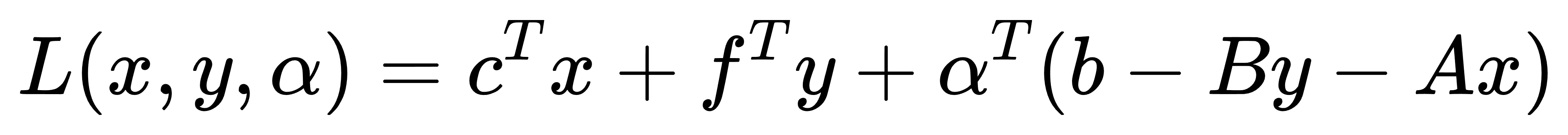
其值域为:
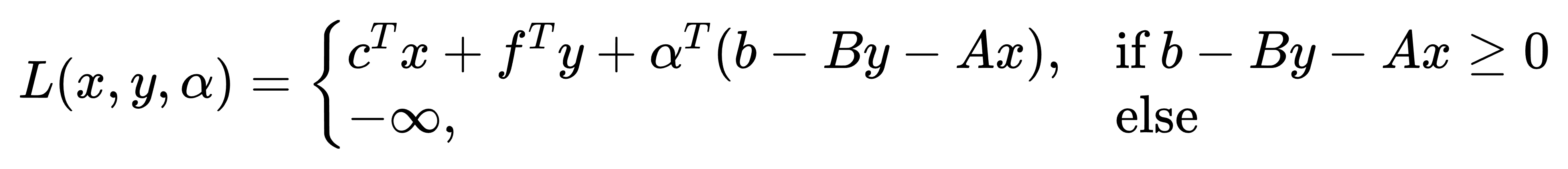
根据对偶理论,Benders主问题中的割平面构造可表示为:
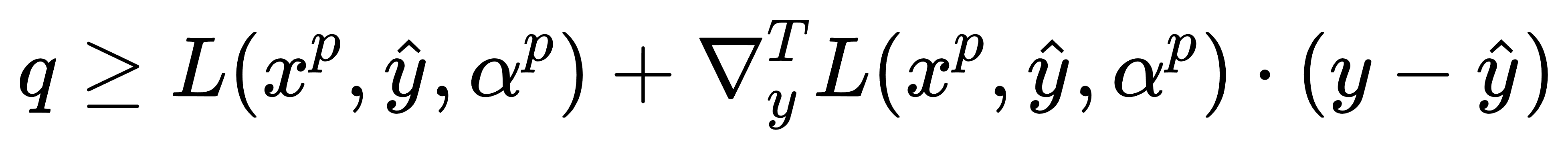
进一步引入函数
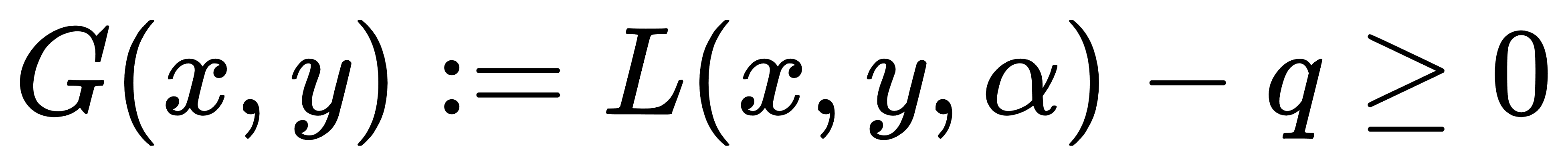
其线性近似为:
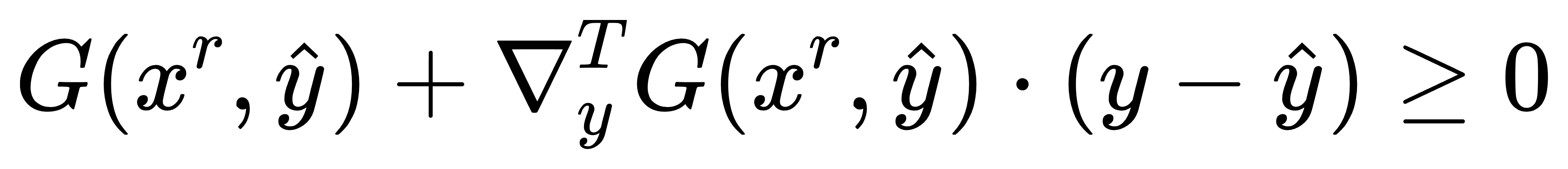
3.2.1 子问题(Sub-Problem, SP)
在实际优化中,割平面的构造需要结合灵敏度信息。我们定义如下形式的子问题(SP):
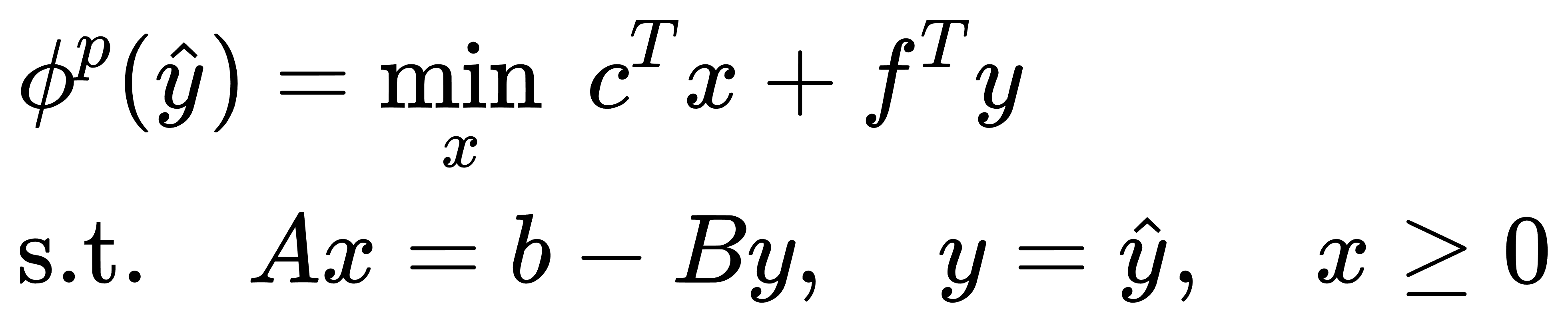
构造主问题割平面时,其形式如下:
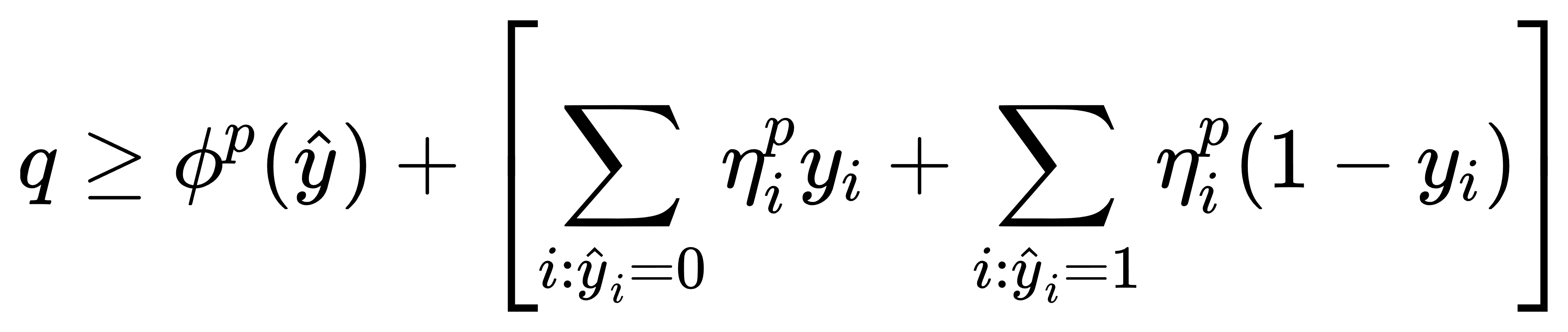
其中,ηip 为灵敏度指标,定义为:
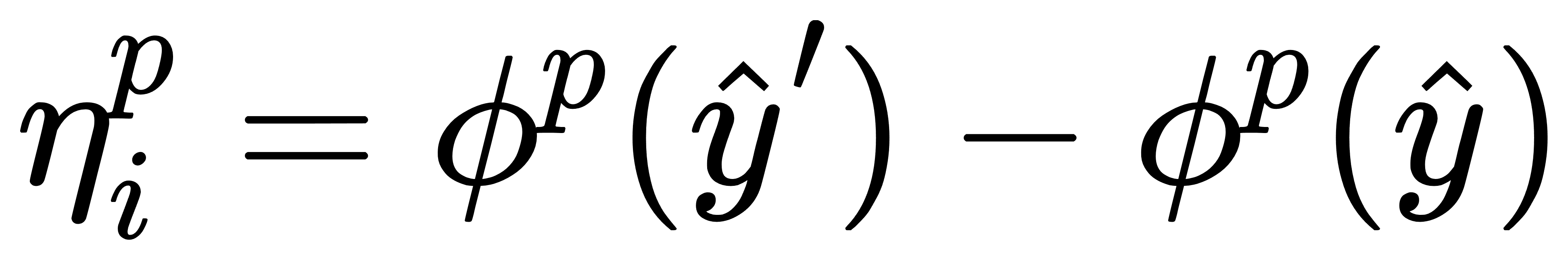
3.2.2 可行子问题(Feasible Subproblem, FSP)
为了判断当前点是否违反了可行性约束,定义如下FSP:
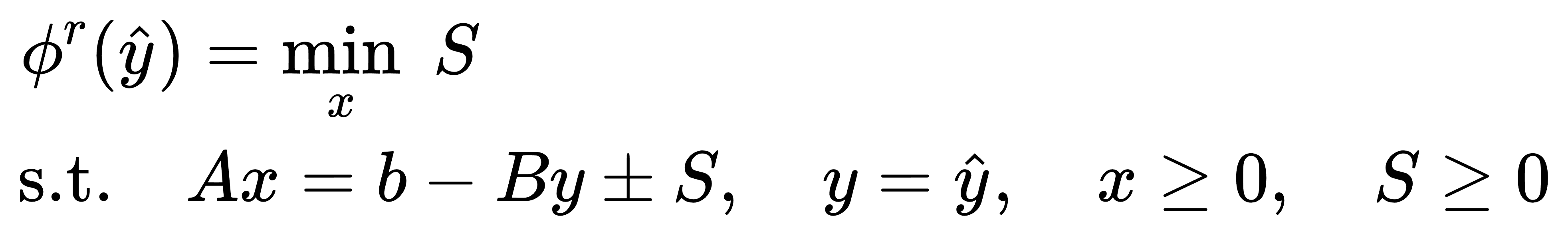
可行性割平面对应表达式为:
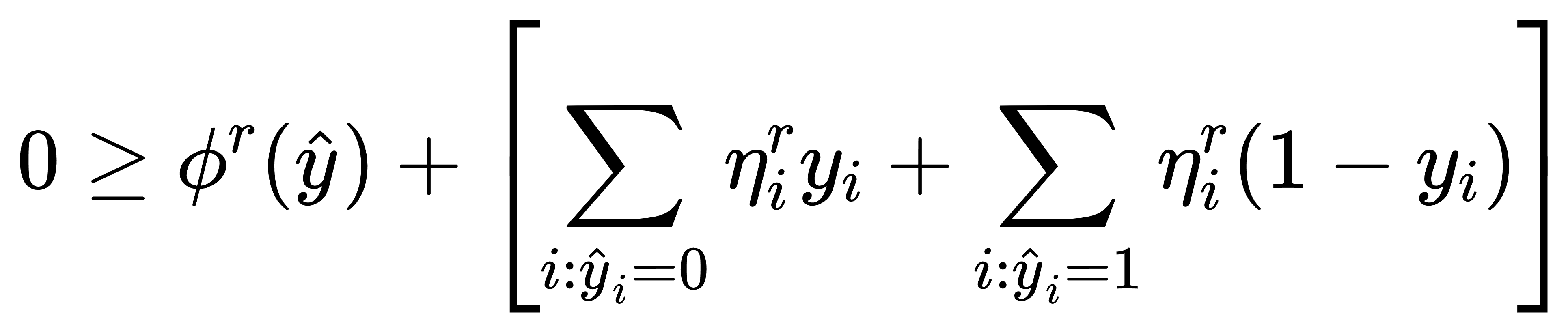
其中同样定义:
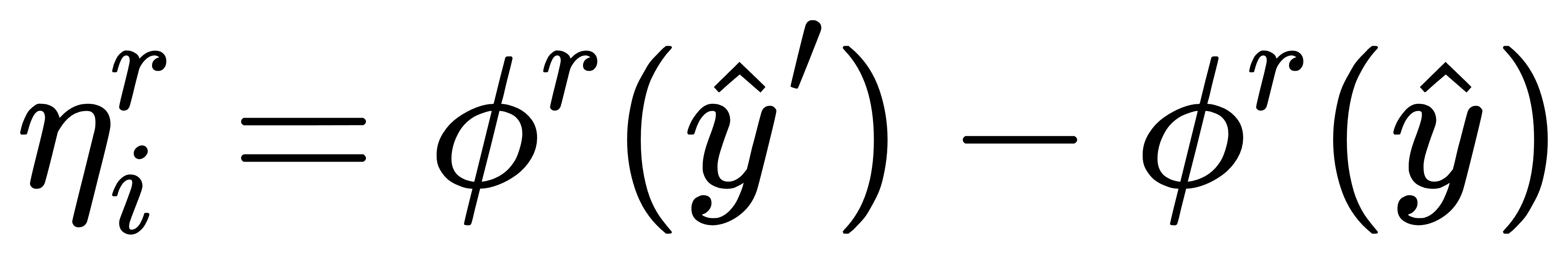
3.2.3 QUBO形式的割平面哈密顿量构造(MP)
在构造主问题的 QUBO 表达时,我们将上述灵敏度形式转写为哈密顿量以适应量子设备。其目标是在保持割平面效用的前提下,对主问题进行二次无约束优化表达。对上式进行QUBO转化后得到如下哈密顿量:
(1) 子问题的 QUBO 哈密顿量 Hp:
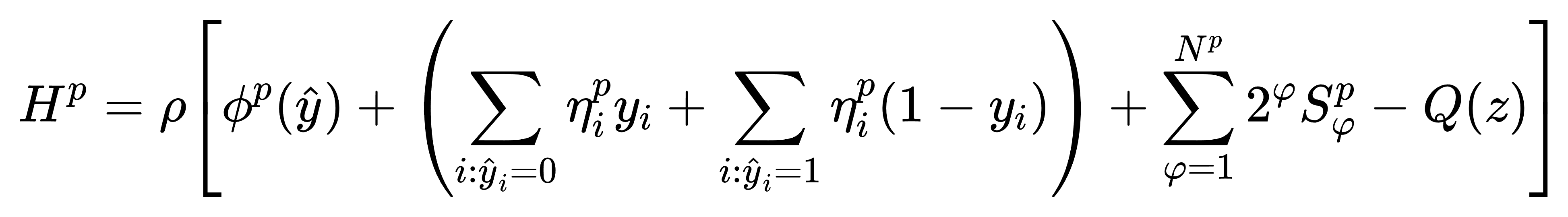
(2) 可行性子问题的 QUBO 哈密顿量 Hr:
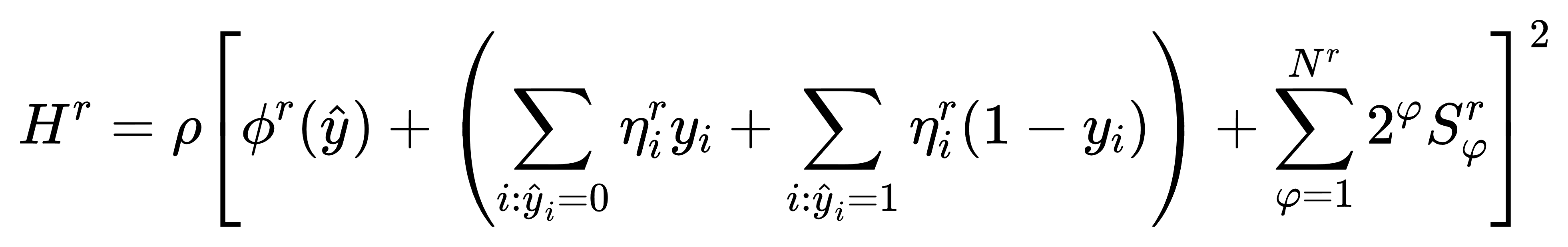
(3) 主问题的整体哈密顿量:
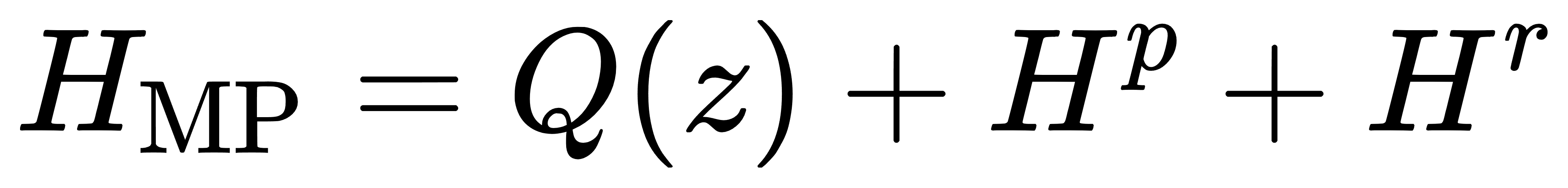
在该主问题中,Q(z) 表示与其他系统变量有关的QUBO项;Hp 和 Hr 分别代表通过灵敏度割平面构造的成本方向与可行性方向的惩罚项。通过不断迭代构造和叠加割平面,主问题可逐步逼近原始联合模型的可行解集。


3.3 模型层级划分与任务调度机制
在前述Benders灵敏度割平面构造的基础上,本文进一步设计了基于模块分解的多阶段分解算法,在变量划分上实现了结构性拆解,更在算法流程中引入了层级主‑从机制与割平面之间的上下交互,构建了一个逻辑严密、资源匹配、计算可并行的求解体系,以此应对系统复杂性、变量耦合性和量子资源稀缺性带来的挑战。原始UC-TS联合模型具有如下结构特征:
离散变量维度高(机组启停 Ui,t、线路通断 Zl,t )
连续变量复杂耦合(出力 Pi,t、潮流 Pl,t、相角 θn,t )
时空耦合强(约束横跨节点、线路、时段)
非线性结构难以标准线性松弛
因此,本文将模型划分为三大模块:
(1) 上层模块(UC模块):负责机组组合相关的离散与连续变量优化
(2) 下层模块(TS模块):处理传输线切换与电网潮流重构
(3) 事故校验模块(Contingency Checking):在预定方案下验证N‑1鲁棒性与稳定性,并提出安全性割平面修正
模块之间的信息交互通过割平面哈密顿量完成。每一模块内部通过构造主问题与子问题划分,使用QUBO形式将主问题传送至光量子伊辛机上进行并行加速,而连续部分由经典计算协同完成。

3.3.1 子问题与主问题的结构性划分
每个模块内部均采用类似结构的主-从分解机制:
子问题(Subproblem) 用于计算给定主变量下的最优连续变量与可行性情况。
主问题(Master Problem) 由多个割平面组合而成,以QUBO形式刻画并交由量子设备加速。
以上层模块为例,其主问题构造如下:
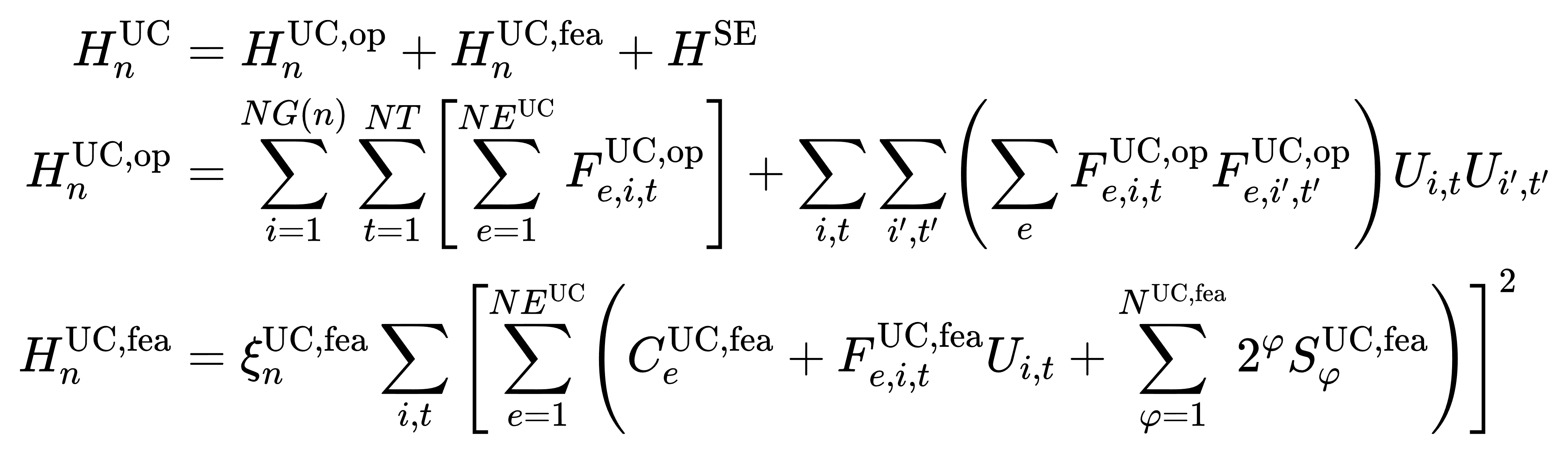
其中 Fe,i,t·、Ce·为灵敏度因子; ξn·为加权系数; $Sφ·为二进制松弛变量; HSE表示事故安全性哈密顿量,由事故校验模块返回。

上下层之间通过可行性割平面与灵敏度割平面互传激活信息:
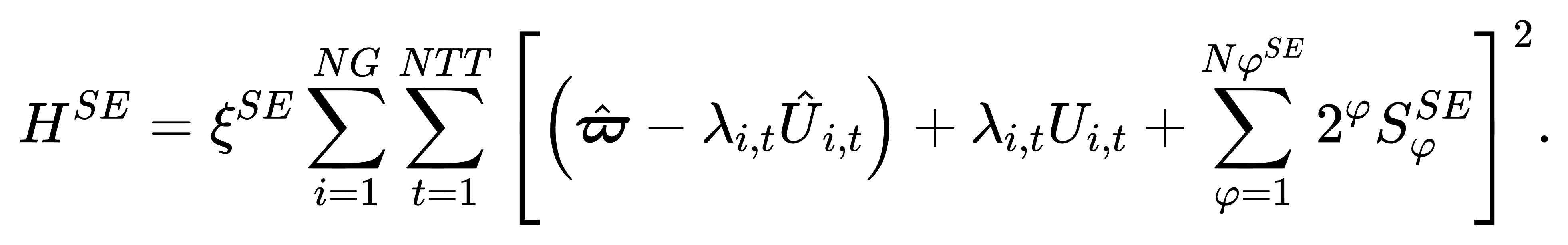
下层模块(TS)则针对线路状态变量 Zl,t 构造如下主问题:
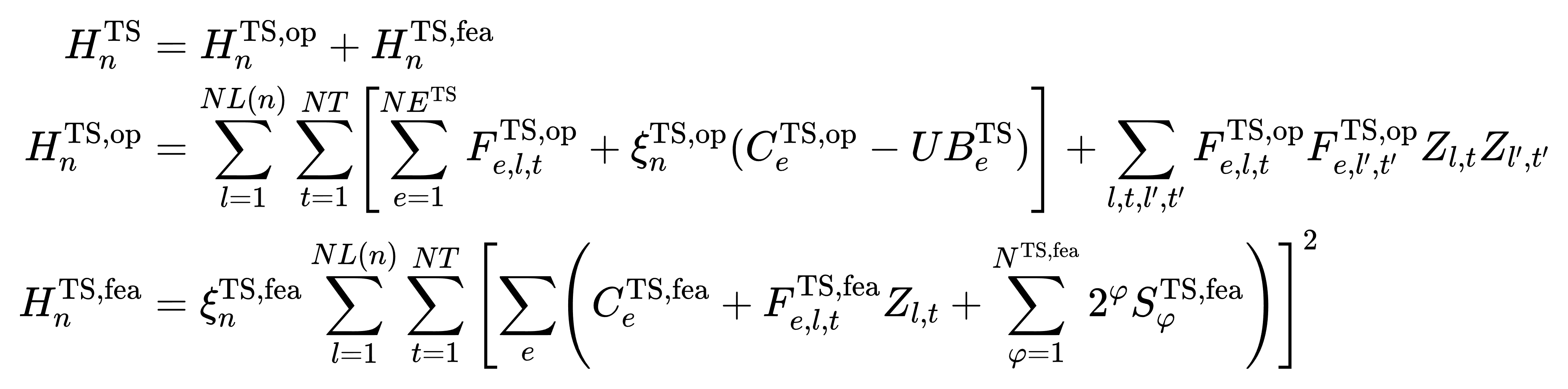

3.3.2 多阶段割平面机制与事故安全修正
三大模块通过“主问题哈密顿量 + 割平面信息”的形式交互,最后一个模块是事故检查模块:
若事故模块发现当前{Ui,t, Zl,t}组合不满足N‑1安全性约束,则向上层返回事故相关的机组割平面 HSE 和传输割平面 HnTS,fea,以更新其哈密顿量;
若子问题无解,则激活可行性松弛子问题并构造约束切割。

最后归纳一下分解算法部分的协同模式如下:
(1) 每一模块以本地子问题派生割平面并构造QUBO主问题;
(2) 多个模块共享公共变量(如潮流相角、联络线功率);
(3) 模块间通过灵敏度信息、共识约束和哈密顿项实现通信;
(4) 量子计算机并行求解主问题,经典计算器处理松弛与梯度计算;
(5) 所有模块满足一定误差界内的割平面收敛条件后终止迭代。
该分解方法不仅显著降低了单体模块的比特需求,还保留了联合优化的全局一致性,有效在当前量子计算能力有限背景下实现了大规模混合整数非线性模型的量子协同求解原型设计。
3.4 平均共识机制
在前述模块化分解框架中,我们已经将复杂的 UC–TS 联合优化问题拆解为多个具有主从结构的子模块。尽管这种模块化显著降低了单一模块的计算维度,但在实际操作中,仍然存在多个模块之间共享变量或逻辑联动的问题,尤其表现在传输线潮流功率、相邻节点相角与功率平衡等物理变量上。为解决模块间耦合变量的一致性问题,本文进一步引入平均共识(Average Consensus)机制,构建了一个多主体、多阶段、多变量同步更新的完全分布式求解框架。
该机制的核心思想是: 每个子模块在不依赖中心协调器的前提下,通过邻接信息的迭代交换,使得相邻模块间对共享变量的局部判断最终收敛于一致,从而在整体上实现系统级的协调优化。
设整个电网被划分为若干节点域(如变电站、区域总线),每个节点 n 内包含本地变量(如机组出力 Pi,t、本地潮流 Pn,mn 等),同时与邻接节点 m∈ Nad(n) 之间存在共享的边界潮流变量 Pn,m+。目标是使得各节点在自主求解本地子问题的基础上,通过对共享变量的一致性约束逐步收敛,即:
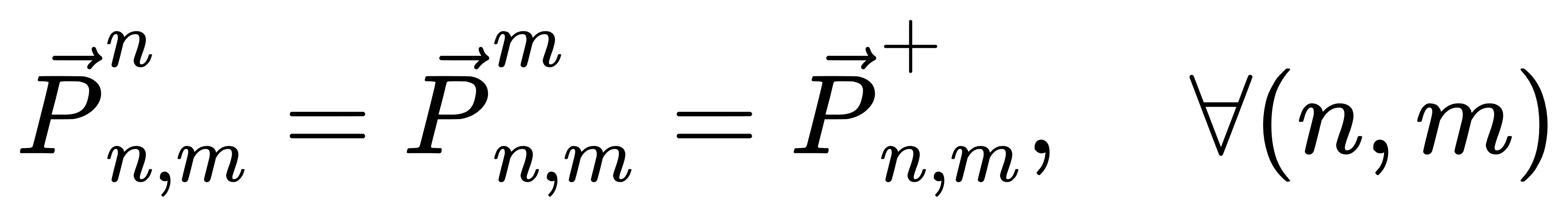
每个节点 n 的局部优化问题如下:
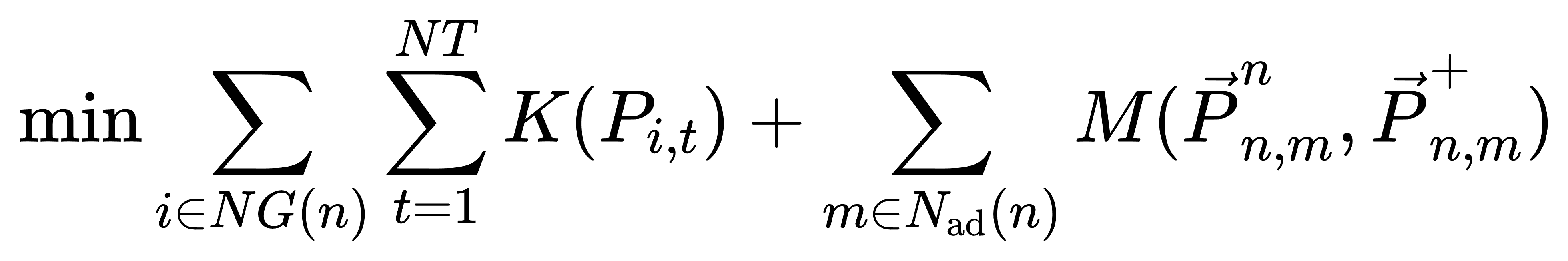
其中 K(Pi,t) = αi Pi,t2 + βi Pi,t 表示机组发电成本; M(·) 是共识代价函数,表示潮流变量差异惩罚项,定义如下:
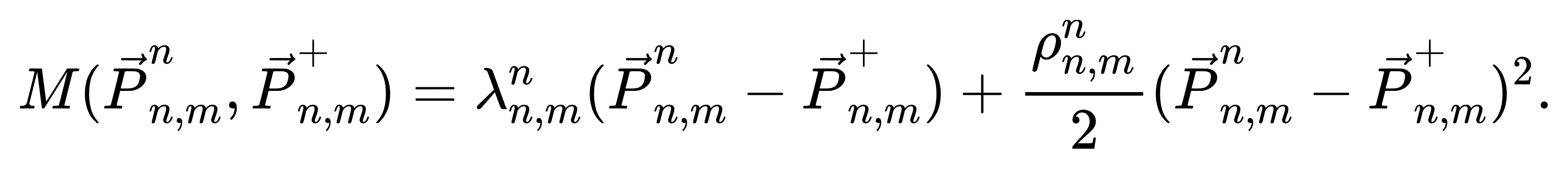
局部约束包括:
(1) 功率平衡:
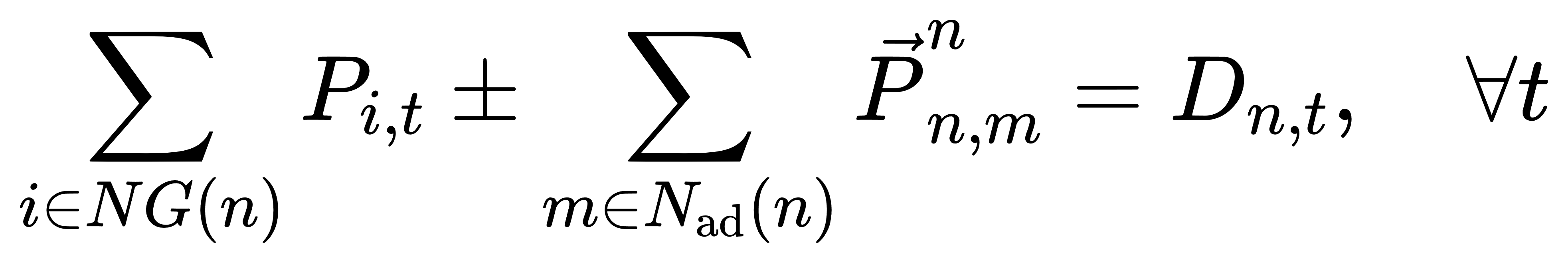
(2) 机组出力限制:
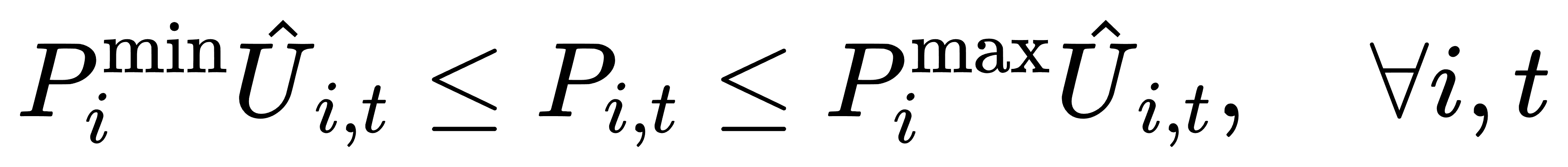
共识耦合变量无显式强制一致,但通过惩罚项诱导收敛。为实现局部变量的全局一致,本文采用如下迭代更新策略:
(3) 变量一致性更新:
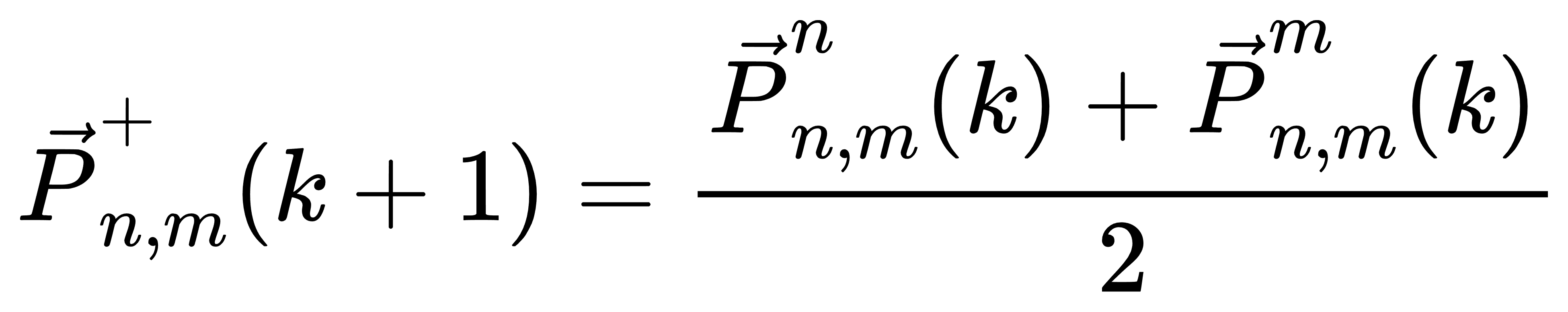
(4) 拉格朗日乘子更新(对偶变量更新):
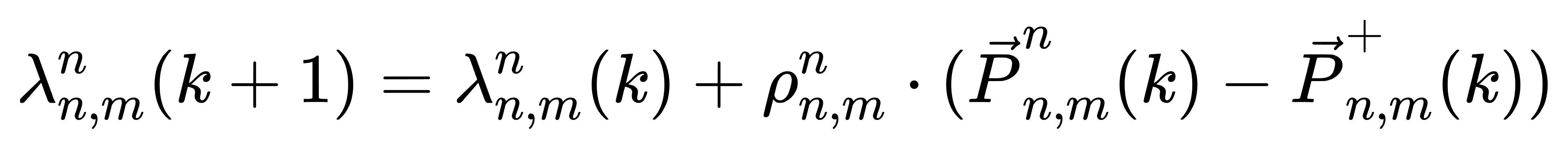
(5) 局部一致性偏差指标:
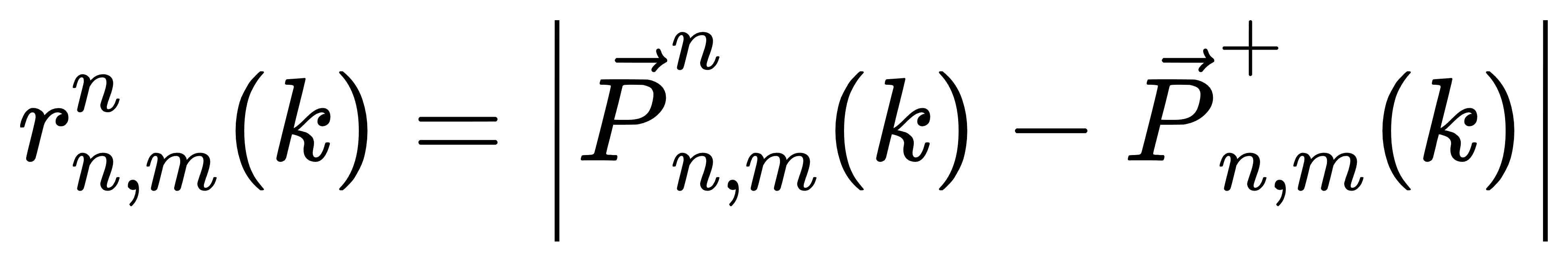
该机制本质上将原问题按区域划分解耦为不同的区域内部的子问题,子问题之间通过共识约束联系,反复迭代使得不同区域的共识变量达成一致,实现分布式并行求解。在每轮迭代中,各节点独立求解本地QUBO问题,仅需与邻接节点交换少量边界变量,极大减少了通信负担并提高了可并行性。为了使该机制落地到量子–经典混合体系中,本文设计如下计算流程:
(1) 每个电网节点配备一个经济调度协调者,连接量子计算设备(求解本地QUBO主问题)与经典比特处理器(负责连续变量优化与对偶变量更新);
(2) 所有节点构成无中心的分布式求解网络,在多个时间段内并行运行;
(3) 每轮迭代中各节点在接收到邻接节点的功率变量后更新本地拉格朗日乘子并重构哈密顿量;
(4) 共识变量作为软约束嵌入本地优化目标,无需硬性同步;
平均共识机制将系统一致性的收敛问题转化为结构性可解的分布式协调问,避免了对全局网络模型的集中表示需求,也规避了量子硬件处理全局变量带来的资源瓶颈。
4. 实验结果
在实验验证部分,本文选取IEEE RTS 24节点系统作为测试平台,对所提出的共识分布式量子多阶段分解算法进行了全面评估,并与传统经典求解器Gurobi 9.0以及量子退火机D-Wave参与的混合算法进行了对比测试。

实验设计覆盖多个调度场景,通过对目标函数值、求解时间、收敛迭代次数以及CPU占用效率等指标的系统性分析,从多个维度考察该算法在实际大规模电力系统优化任务中的表现,进一步检验其在计算效率、可扩展性和求解质量方面的量子优势。
首先,在目标函数优化能力方面,本文设计了三个逐渐增加复杂性的典型场景(编号为5、6、7),分别评估经典Gurobi、D-Wave量子退火机协同算法(Gurobi+D-Wave)以及本文提出的Gurobi+光量子计算机协同算法的性能。在目标函数结果上,各算法在场景5中得分一致(738159.68),而在场景6和7中,本文算法与D-Wave算法结果相同(740095.81和759120.52),均优于Gurobi(740118.16和761688.25),表明在优化目标上,量子分解算法并未因结构分解而降低解的质量,反而在某些复杂度更高的场景下表现出更优的全局搜索能力。
在迭代性能方面,三个算法在上层主问题迭代次数上几乎保持一致,场景5至7分别为5、6、6次;而下层模块的迭代次数随场景复杂度增加呈现上升趋势,从24到102再到50,说明下层模块承担了更复杂的网络拓扑重构与事故校验任务。值得注意的是,即便在下层任务密度增加的情况下,算法整体仍能稳定收敛,展现出良好的算法鲁棒性和工程可控性。

当然,最显著的性能提升体现在求解时间上。在场景7中,Gurobi求解时间为58.2秒,D-Wave方案为11.3秒,而本文所采用的光量子协同算法仅需不到2.22秒,时间缩短比例高达96.2%。同样,在场景6中该算法的求解时间小于3.52秒,相比于Gurobi的48.5秒节省了超过92%。这种数量级的求解加速在传输线切换与机组组合联合优化等高维复杂问题中极为罕见,直接体现了光量子计算机在QUBO结构问题求解中的物理计算优势。此外,在CPU占用方面,经典Gurobi在场景5中消耗10.3秒CPU时间,D-Wave方案消耗7.3秒,而本文方法仅需0.0268秒,表明其在混合协同计算架构下实现了对计算负载的高度转移与解耦,极大地提升了能效比。

算法不仅在数值表现上取得显著优势,其在电网动态响应与拓扑调节的可视化结果也提供了直观验证。通过提取5条代表性传输线在24小时内的通断状态轨迹,以及多个关键节点的出力随时间的波动曲线,可以观察到系统能够在保有稳定供电能力的前提下,根据负荷需求与网络状态变化灵活调配潮流与发电计划。这种响应能力在调度突发事故、电力负荷剧变或新能源出力波动等场景下具有实际应用价值。此外,动态模拟图中不同节点火电机组的开机状态随时间推移而演化,黄色的激活区域清晰地展现了算法对系统运行边界的有效控制与节奏感知。
值得一提的是,随着问题复杂度的增加,本文方法的优势并未减弱,反而展现出规模越大、加速越强的非线性增长趋势。在最复杂的测试场景下,求解时间从传统方法的58秒骤降至不足2.3秒,且目标函数优化质量不降反升。相比D-Wave量子退火机方案,光量子方案进一步将计算时间压缩至原有的20%以下,印证了光量子技术在大规模二进制组合优化中所具备的物理并行与低延迟特性。最终,该算法在求解效率、解质量与可扩展性三方面均表现优异,为在真实调度系统中部署大规模、实时、耦合复杂的能源调度任务奠定了技术基础。
5. 总结
本文的工作主要集中在模型、算法和实验三个方面:
(1) 模型方面: 根据优化功能将原问题划分为多个模块,通过传递割平面哈密顿量实现信息交互,最终实现“分而治之”地求解。、
(2) 算法方面: 基于松弛问题的构造和灵敏度分析开发高效的多阶段分解算法,QUBO主问题采用玻色量子公司开发的光量子相干伊辛机加速求解。每个节点根据共识独立且并行的求解共识约束的局部问题,模型规模降低,大幅提升了联合优化问题的求解效率
(3) 实验方面: 利用量子计算在求解QUBO问题上的优势,提出了集中式与共识分布式的多阶段量子分解算法。基于 6-节点系统在多个不同场景下与Gurobi9的对比实验表明了集中式量子分解算法在求解机组组合与传输线切换联合优化问题的有效性,而在IEEE RTS 24-节点系统上的对比实验表明量子分解算法的计算结果和求解时间相对经典商用求解器Gurobi9更具优势,验证了共识分布式量子分解算法在求解大规模机组组合与传输线切换联合优化问题上的优越性。
Reference
[1] K. W. Hedman, M. C. Ferris, R. P. O'Neill, Co-optimization of generation unit commitment and transmission switching with N-1 reliability, IEEE Transactions on Power Systems, 2010, 25(2), 1052-1063.
[2] M. Sheikh, J. Aghaei, A. Letafat, M. Rajabdorri, T. Niknam, M. Shafie-Khah, J. P. Catalão, Security-constrained unit commitment problem with transmission switching reliability and dynamic thermal line rating, IEEE Systems Journal, 2019, 13(4), 3933-3943.
[3] J. Lin, Y. Hou, G. Zhu, S. Luo, P. Li, L. Qin, L. Wang, Co-optimization of unit commitment and transmission switching with short-circuit current constraints, International Journal of Electrical Power & Energy Systems, 2019, 110, 309-317.
[4] R. Saavedra, A. Street, J. M. Arroyo, Day-ahead contingency-constrained unit commitment with co-optimized post-contingency transmission switching, IEEE Transactions on Power Systems, 2020, 35(6), 4408-442.
相关内容链接
1. PPT链接:https://pan.baidu.com/s/1k4Q2icBJnuCFKhdfNNl9zQ?pwd=qez8,提取码: qez8
2. 讲座回放链接:https://www.bilibili.com/video/BV1fCfwYtEcA/?vd_source=4a5d2780500d852e3e0484c6a4e1e059 | 























