文章概要:本文提出了一种训练量化神经网络(QNN,Quantized Neural Network)的Ising算法,该算法结合拓扑网络的二值表示和损失函数的降阶方法,实现量化神经网络到二次约束二值优化问题(QCBO)再到二次无约束二值优化问题(QUBO)的转变,使其能够在量子计算机(如相干伊辛机CIM)进行求解。通过在用Fixstars Amplify AE进行三个实验 (1)QCBO公式的正确性(2)QCBO和QUBO解的同一性(3)QUBO的可解性的验证举例 ,在简化的MNIST中分类准确率达到98.3%,说明了该算法在训练QNN网络的可行性、科学性和可靠性。
一、研究背景
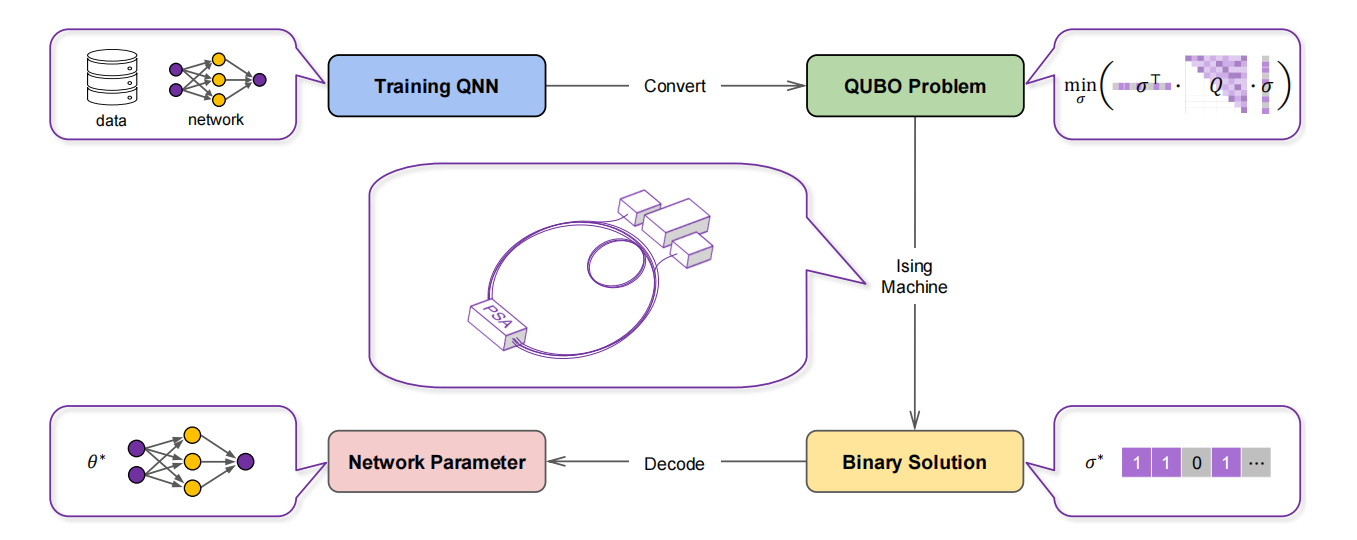
近年来,Ising机器作为一种专用的量子设备,因其在毫秒级时间内求解大规模二元优化问题的能力而备受关注,Ising机器能够高效处理二次无约束二元优化(QUBO)问题,为神经网络的训练提供了新的可能性。
那么就会提出问题:能否将传统神经网络的训练问题转移到Ising机器上进行处理求解呢?
其一,传统的前馈神经网络训练主要依赖梯度下降算法,Ising机器处理的是离散二进制的二元二值优化问题,二者在计算范式上存在差异,这便使得传统方法无法直接套用在Ising机器上;其二,多层前馈神经网络是由输入层、隐藏层、输出层构成,层与层之间存在一些线性运算和非线性运算(激活函数),构成了神经网络的复杂函数关系;
为解决上述问题,本文提出了将量化神经网络(QNN)通过将复杂的网络函数关系转化为等式约束,将网络参数量化为离散值,转化为带有约束的二元优化问题(QCBO),再通过惩罚函数和Rosenberg降阶法,转化为二元无约束优化问题(QUBO),使其能在Ising机上求解。
回顾前人工作:Ising机的快速计算能力可以应用于训练深度神经网路,目前,已经被用于机器学习,如:支持向量机、聚类模型等;B¨ohm利用超快统计抽样成功训练了表达能力受限的玻尔兹曼机;Niazi等人在稀疏伊辛机上训练整个神经网络,受限于其运算速率;Lay-devant等人利用平衡传播的方法训练动态能量网络,受限于精度值。
二、论文关键部分建模解析
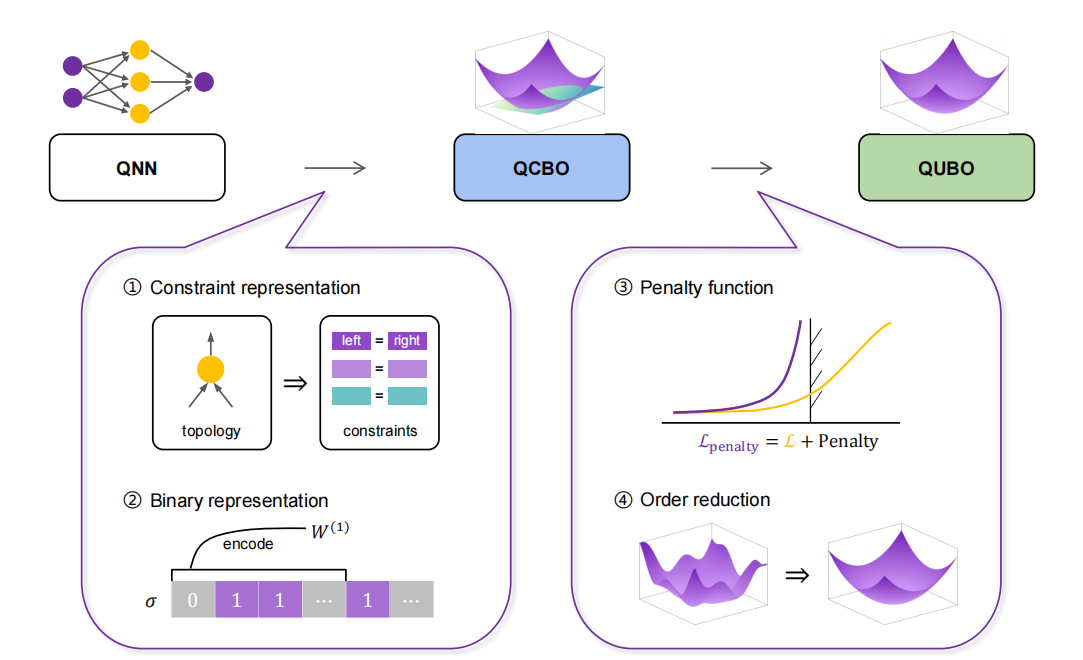
整体思路:本文将QNN的训练问题采用了等式约束和二值化表示方法转换为二次约束二值优化问题(QCBO),进一步通过惩罚函数和Rosenberg降阶方法转化为二次无约束二值优化问题(QUBO),最后在量子计算机上求解。

论文中用到得一些数据量:

2.1 问题总结概述
QNN的训练问题采用均方误差损失函数(MSE)作为优化函数,利用伊辛机训练其量化参数

其中,N为数据集的大小
目标函数的设定:

2.2 QNN到QCBO的转化
QNN作为一种前馈神经网络,由大量神经元构成,每个神经元都会经过线性变换和激活的操作。为了在优化过程中捕获网络拓扑,将上述两个操作通过变换成等式约束准确捕获网络拓扑的前后连接,并将网络参数量化离散为二进制数,转化为QCBO模型
在本文中QNN的网络建构选择了具有等宽隐藏层的全连接网络,采用符号函数(sign)作为激活函数。
2.2.1 线性变换和激活的等式约束:通过将QNN网络复杂的函数连接关系,分类讨论每一层的函数关系,转化为等式约束;实现由等式关系表示神经网络复杂的拓扑关系。
针对线性变化的等式约束,我们有:

对于sign激活函数的等式约束,考虑到可能为0值得情况,我们定义下式:

上述的不等式中,我们再引入一个辅助变量 ,将其转化为等式,方便后面惩罚函数的构建。 ,将其转化为等式,方便后面惩罚函数的构建。

现在,我们参照QNN的设计框架,具体化每一层的等式约束
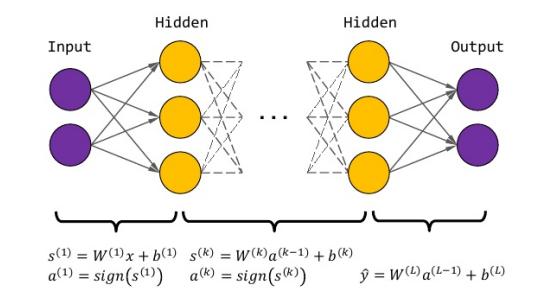
对于第一层

接下来的2,3,......,L-1层

对于第L层:

2.2.2 二值化表示:所有的输入、权重、偏置、预激活值和激活值以及中间变量通过二进制编码协议表示为二元变量。通过2的幂次方和的形式,转换为二进制,转换方式如下:

同样的,依据QNN的网络构建,我们可以细化每一层中网络参数的二值化;且基于’每一个网络参数的位数应该与十进制变量的值范围一致‘这一原则,我们可以得出每一个参数值的范围。(详见论文的附录D)
经上述等式约束和二进制转化操作过后,我们将QNN复杂的网络拓扑训练问题转化为QCBO问题,目标问题转化为下式:

2.3 由QCBO到QUBO的转变
QCBO问题无法直接部署在Ising机上进行求解,因此需要转化为无约束问题(QUBO)。在此过程中我们利用了惩罚函数和Rosenberg降阶的方法,转化过程思路如下:

2.3.1 惩罚函数
上述在转化过程中,定义了等式约束来表示网络拓扑,我们将约束条件引入到目标函数中,当ρ足够大时,违反约束的代价大于提高预测精度的代价,这有利于满足等式约束,从而求解有约束优化问题。
我们将上一步转化过程中得到的等式约束,加上惩罚因子,作为惩罚项,加入到目标函数中

2.3.2 Rosenberg 降阶法
通过Rosenberg多项式的方法降低损失函数的阶数,从而得到一个二次无约束损失函数(QUBO问题)。在实验的每一次步骤中,我们定义一个辅助变量代替损失函数中出现频率最高的两个二元变量的乘法,并将Rosenberg多项式添加到具有较大系数的损失函数中去(这里也有上述惩罚函数的思想)。

Rosenberg多项式的一般形式为:

其中u为被代替的两个二元变量,v为辅助变量。
利用Rosenberg降阶法,不断通过一阶因子替代,最终实现降阶,得到二次损失函数,成功将训练QCBO问题转化为QUBO问题。

至此我们就将QNN的训练问题转化为可供Ising机求解的QUBO 问题
3、实验结果
为了证明Ising学习算法的正确性,本文中做了三个实验进行验证:(1)检查QCBO公式的正确性(2)验证QUBO和QCBO解的同一性(3)验证QUBO在经典Ising机上的可解性。
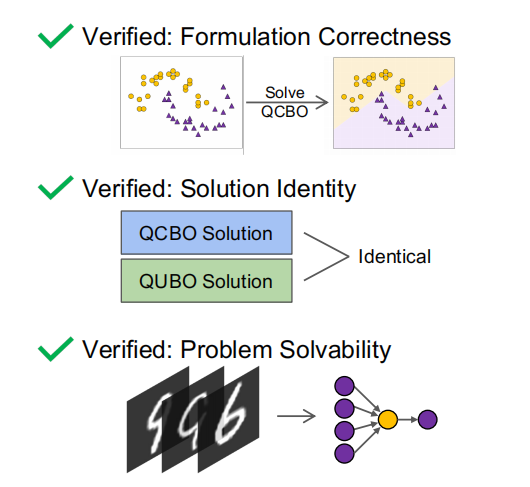
(1)检查QUBO公式的正确性,通过加检查训练的网络是否能正确拟定给定的数据集来验证:使用了一个双月形状的的数据集,包含了50个带有两种标签的样本;构建一个具有一个隐藏层,包含3个隐藏神经元的网络,利用Gurobi optimizer求解,结果显示,损失达到0.31,准确率高达98%,成功验证QCBO公式的正确性。
(2)验证QUBO和QCBO解的同一性:通过对QCBO和QUBO分别进行实验,其中利用Gurobi optimizer求解QCBO问题;采用tree decomposition的方法分解QUBO的求解过程;
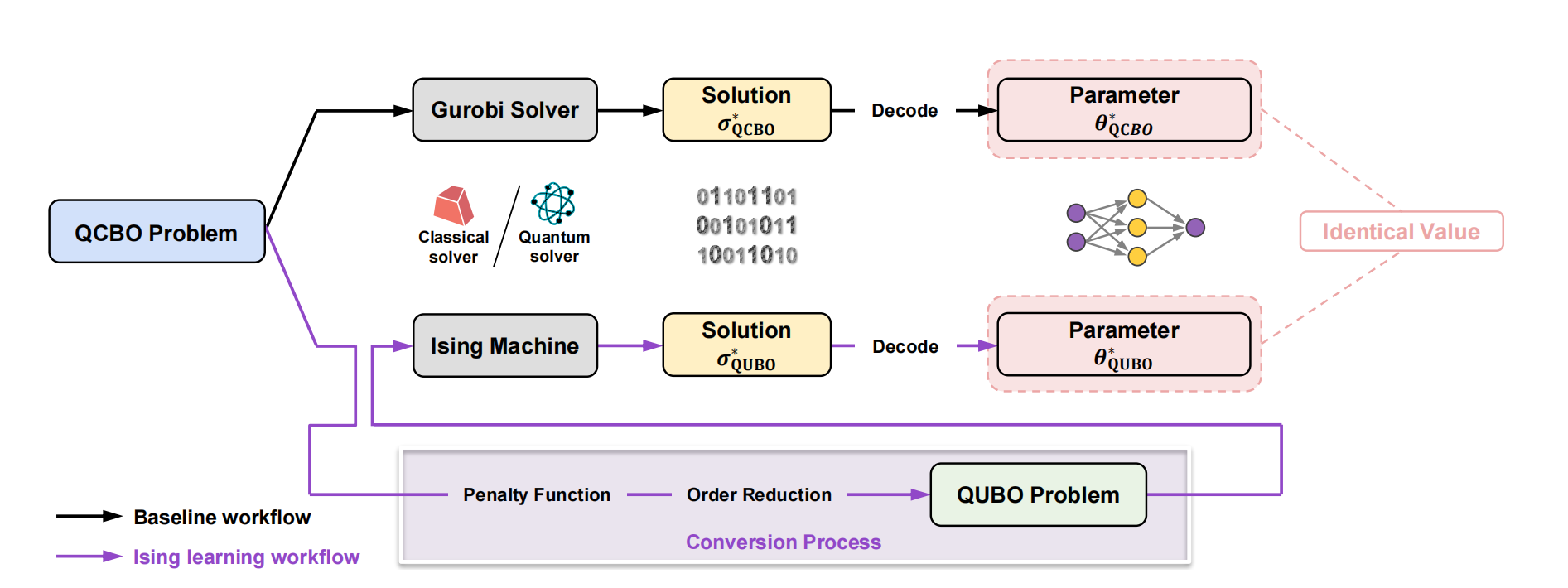
对比前后实验的二进制变量的数量、模型的求解结果、损失和准度等,证实了QCBO转化为QUBO后并不改变解。

(3)验证QUBO的可解性:我们使用MNIST手写数据集中的6和9两个数字作为数据集,选取了4张图像(2张6,2张9)作为训练子集
图像的预处理:1、将训练图像进行裁剪,裁剪出黑色的边缘;2、将图像分割为4个块(2*2);3、对每一个patch中的白色像素个数进行计数;4、根据白色像素的数量归一化为{-1,0,1}.
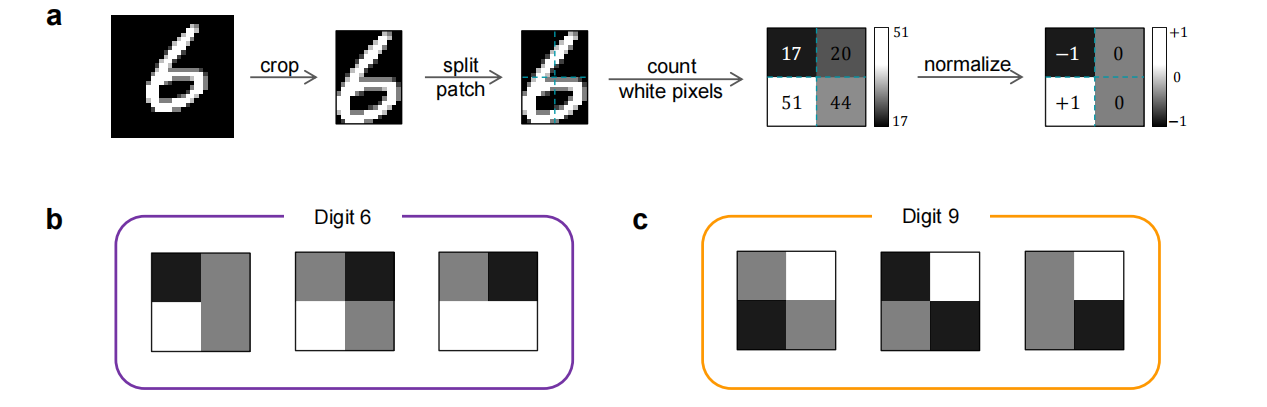
定义QNN的网络:构建具有一个隐藏层的和一个隐藏单元的QNN,输入层有4个单元,对应接受图像中的一个像素值,最后一层的输出值在[-1,+1]范围内,-1代表数字9,反之代表数字6。
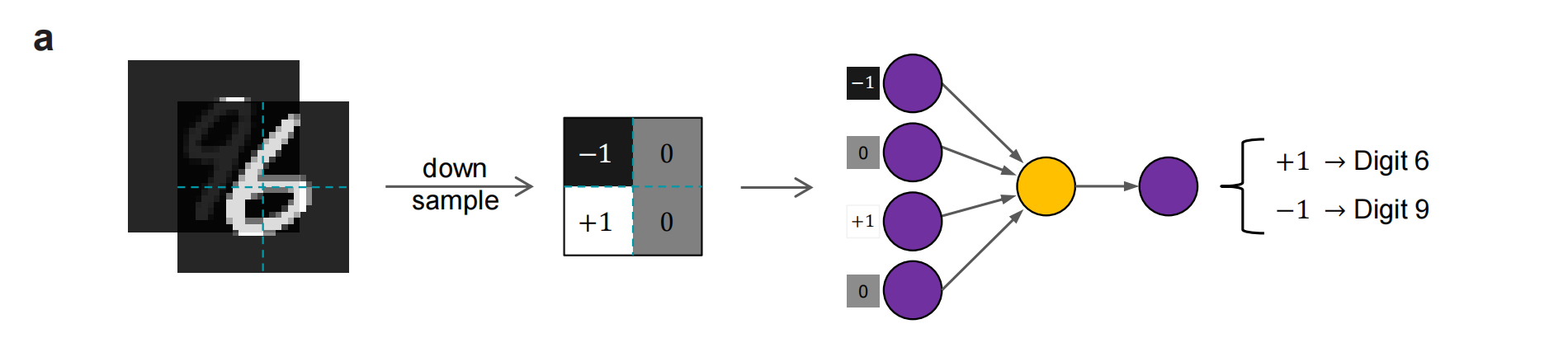
我们在Fixstars Amplify AE (GPU模型的Ising机)上进行实验,设置退火时间为700ms,输出损失直方图如下:
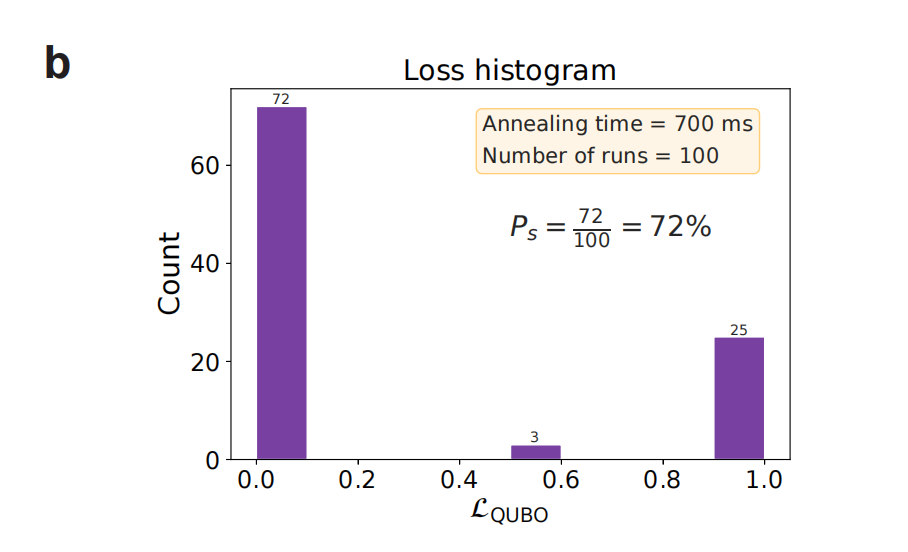
文中定义了另一个指标TTS(Time-to-solution):

图像中看出,在实验中TTS为2.53s,当退火时间设置为2.53s时,有99%的成功率可以找到最优的网络参数。成功验证了QUBO的Ising机上的可解性!
4、总结
本文利用Ising机器求解速度的特性对量化神经网络QNN提出了一种创新性训练算法,通过将QNN的训练问题转化为二次有约束二值优化问题,后通过降阶和惩罚转化为二次无约束优化问题(QUBO),通过实验证明了该算法的科学性和正确性,为神经网络训练提供了新的计算范式。
论文链接:https://arxiv.org/abs/2311.03408
| 









