本帖最后由 graphite 于 2025-8-13 18:03 编辑
本文围绕生物医学 AI 中的变分自编码器(VAE)展开,分为上下两部分。本部分为上半部分,将详细介绍 1-2 章内容(全文目录如下文所示),涵盖 VAE 相关的方法基础,包括问题场景界定、变分边界推导、关键算法(如 SGVB、AEVB)、重参数化技巧,以及 VAE 的具体示例、相关工作对比、实验验证等核心技术内容,为理解 VAE 的原理与应用奠定基础。
《 Auto-encoding variational bayes 》一文聚焦生物医学 AI 中的变分自编码器(VAE),先阐述其方法基础,涉及有向图模型下界估计、问题场景(难解性与大数据集挑战)、变分边界、SGVB 估计器、AEVB 算法及重参数化技巧,还以具体示例说明 VAE 结构,对比相关工作,介绍实验及结论与未来方向,展现 VAE 在处理连续潜变量等方面的技术细节与应用潜力。
全文目录
1. 论文说明
2. 论文速读
3. 变分自编码器(VAE)的理解
1. 论文说明
Kingma D P, Welling M. Auto-encoding variational bayes[J]. arXiv preprint arXiv:1312.6114, 2013. 【累计引用30000余次】

1.1 作者介绍
Google大脑研究科学家: Diederik P. Kingma
微软研究院科学智能中心 (MSR AI4Science)杰出科学家,阿姆斯特丹大学机器学习教授Max Welling
1.2 个人总结
参考资料:
变分自编码器:https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73
变分推断:https://towardsdatascience.com/bayesian-inference-problem-mcmc-and-variational-inference-25a8aa9bce29
关于变分自编码器的相关总结:
本文提出了自编码变分贝叶斯(Auto-Encoding Variational Bayesian, AEVB)算法。在自编码变分贝叶斯(AEVB)算法中,研究者们通过使用随机梯度变分贝叶斯(SGVB)估计器来优化识别模型,使推理和学习特别有效。
变分自编码器可以被定义为一种自编码器,它的训练是正则化的(regularised),以避免过拟合,并确保潜在空间具有良好的属性,使生成过程成为可能。
自动编码器的潜在空间的规律性是一个难点,它取决于数据在初始空间中的分布、潜在空间的维度和编码器的体系结构。 相对而言,变分自编码器(VAE)通过正则化获得了连续性和完整性(continuity and completeness),倾向于在潜在空间中编码的信息上创建一个“梯度”,而非点分布(punctual distribution)。
与生成对抗网络(GAN)中的对抗性训练概念的简单性相比,变分自编码器(VAE)理论基础(概率模型和变分推断)的复杂性更高。
变分自编码器(VAE)在微生物组中的应用:
宏基因组分箱: Nissen J N, Johansen J, Allesøe R L, et al. Improved metagenome binning and assembly using deep variational autoencoders[J]. Nature biotechnology, 2021, 39(5): 555-560.
多组学与药物关联: Allesøe R L, Lundgaard A T, Hernández Medina R, et al. Discovery of drug–omics associations in type 2 diabetes with generative deep-learning models[J]. Nature biotechnology, 2023, 41(3): 399-408.
宏基因组分箱: Lindez P, Johansen J, Sigurdsson A I, et al. Adversarial and variational autoencoders improve metagenomic binning[J]. 2023.
基于微生物组的疾病预测: Oh M, Zhang L. DeepMicro: deep representation learning for disease prediction based on microbiome data[J]. Scientific reports, 2020, 10(1): 6026.
2. 论文速读
2.1 摘要
我们如何在有向概率模型(directed probabilistic models)中,在具有难以处理的后验分布的连续潜在变量和大型数据集的存在下,执行有效的推理和学习? 我们介绍了一种随机变分推断和学习算法(a stochastic variational inference and learning algorithm),它可以扩展到大型数据集,并且在一些温和的可微性条件(some mild differentiability conditions)下,甚至可以在棘手的情况下工作。我们的贡献是双重的。首先,我们展示了变分下界的重新参数化产生了一个下界估计量(a reparameterization of the variational lower bound yields a lower bound estimator),可以使用标准随机梯度方法(standard stochastic gradient methods)直接优化。其次,我们表明,对于每个数据点具有连续潜在变量的独立同分布(Independent Identically Distribution,IID)数据集,通过使用所提出的下界估计量将近似推理模型(approximate inference model, 也称为识别模型)拟合到难以处理的后验,可以使后验推理特别有效。理论优势体现在实验结果上。

补充图1: 有向概率图模型的相关解释,参考邱锡鹏老师《神经网络与深度学习》第11.1节。
2.2 引言
我们如何使用有向概率模型进行有效的近似推理和学习,其连续潜在变量和/或参数具有难以处理的后验分布? 变分贝叶斯(Variational Bayesian, VB)方法涉及到难以处理的后验的近似优化。不幸的是,一般的平均场方法 (mean-field approach)对于近似后验(approximate posterior)需要期望的解析解,这在一般情况下也是难以处理的。我们证明了变分下界的再参数化如何得到下界的一个简单的可微无偏估计(a simple differentiable unbiased estimator);这种随机梯度变分贝叶斯(Stochastic Gradient Variational Bayes, SGVB)估计器可以用于几乎任何具有连续潜在变量和/或参数的模型的有效近似后验推理(efficient approximate posterior inference),并且使用标准随机梯度上升技术(standard stochastic gradient ascent techniques)可以直接优化。
对于独立同分布(i.i.d)数据集和每个数据点连续潜在变量的情况,我们提出了自编码变分贝叶斯(Auto-Encoding Variational Bayesian, AEVB)算法。在自编码变分贝叶斯(AEVB)算法中,我们通过使用随机梯度变分贝叶斯(SGVB)估计器来优化识别模型,使推理和学习特别有效,该模型允许我们使用简单的祖先采样(simple ancestral sampling)执行非常有效的近似后验推理(approximate posterior inference),这反过来又允许我们有效地学习模型参数,而不需要昂贵的迭代推理方案(如马尔可夫链蒙特卡洛, 即MCMC)每个数据点。学习到的近似后验推理模型也可以用于许多任务,如识别(recognition)、去噪(denoising)、表示(representation)和可视化(visualization)目的。当神经网络用于识别模型(recognition model)时,我们就得到了变分自编码器(variational auto-encoder)。
2.3 方法
本节中的策略可用于推导具有连续潜变量的各种有向图模型的下界估计量(a lower bound estimator,随机目标函数)。我们将在这里限制自己于常见情况,即我们有一个具有每个数据点潜在变量的独立同分布(i.i.d.)数据集,并且我们喜欢对(全局)参数执行最大似然(maximum likelihood, ML)或最大后验(maximum a posteriori, MAP)推理,以及对隐变量进行变分推断(variational inference)。比如说,很容易将这种情况扩展到我们也对全局参数执行变分推断(variational inference on the global parameters)的情况;该算法放在附录中,但这种情况下的实验将留给未来的工作。请注意,我们的方法可以应用于在线、非平稳设置,例如流数据(streaming data),但这里为了简化,我们假设一个固定的数据集。
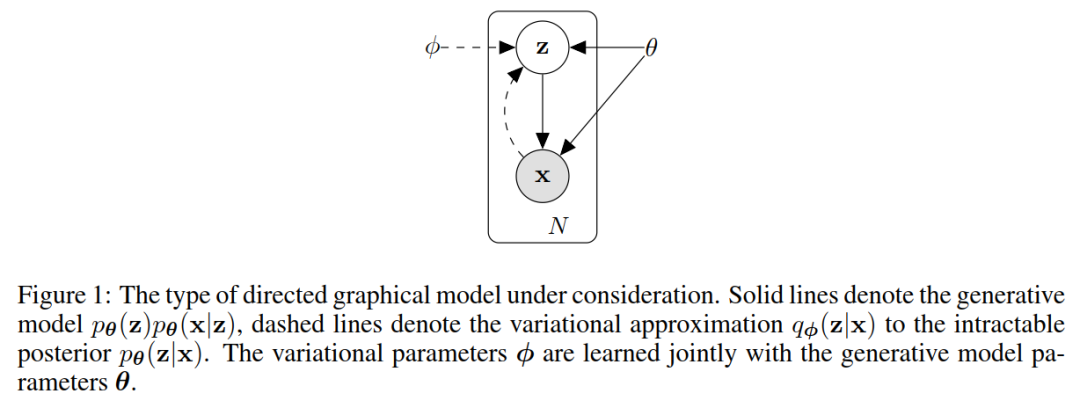 图1:所考虑的有向图模型类型。 图1:所考虑的有向图模型类型。
2.3.1 问题场景
让我们考虑由一些连续或离散变量的 𝑁 个独立同分布(i.i.d)样本组成的数据集 𝑋={𝑥(𝑖)}𝑖=1𝑁 。我们假设数据是由一些随机过程生成的,涉及一个未观察到的连续随机变量 𝑧 。该过程包括两个步骤:(1) 𝑧(𝑖) 的值是由一些先验分布 𝑝𝜃(𝑧) 生成的;(2)由某个条件分布 𝑝𝜃(𝑥|𝑧) 生成一个值 𝑥(𝑖) 。我们假设先验的 𝑝𝜃(𝑧) 和似然的 𝑝𝜃(𝑥|𝑧) 来自分布 𝑝𝜃(𝑧) 和 𝑝𝜃(𝑥|𝑧) 的参数族,并且它们的概率密度函数(probability density functions, PDFs)对于 𝜃 和 𝑧 几乎在任何地方都是可微的。不幸的是,这个过程的很多都隐藏在我们的视野之外:真正的参数 𝜃 以及潜在变量的值对我们来说是未知的。
非常重要的是,我们没有对边际概率或后验概率(marginal or posterior probabilities)做出常见的简化假设。相反,我们在这里感兴趣的是一种通用算法,它甚至可以在以下情况下有效地工作:
1. 难解性(Intractability):边际似然的积分 𝑝𝜃(𝑥)=∫𝑝𝜃(𝑧)𝑝𝜃(𝑥|𝑧)𝑑𝑧 难以处理(因此我们无法评估或区分边际似然),真实后验密度 𝑝𝜃(𝑧|𝑥)=𝑝𝜃(𝑥|𝑧)𝑝𝜃(𝑧)𝑝𝜃(𝑧) 难以处理(因此最大似然估计算法不能使用),并且任何合理的平均场变分贝叶斯(VB)算法所需的积分也是难以处理的情况。这些难解性是相当普遍的,并且出现在中等复杂的似然函数 𝑝𝜃(𝑥|𝑧) 的情况下,例如具有非线性隐藏层的神经网络。
2. 庞大的数据集(A large dataset):我们拥有如此多的数据,批量优化成本太高;我们希望使用小批量甚至单个数据点进行参数更新。基于采样的解决方案,例如蒙特卡罗极大似然估计(Monte Carlo EM),通常太慢,因为它涉及每个数据点典型的昂贵采样环路
我们对上述场景中的三个相关问题感兴趣,并提出了解决方案:
1. 对参数 𝜃 的有效近似最大似然(ML)或最大后验估计(MAP)估计。参数本身可能是有意义的,例如,如果我们正在分析一些自然过程。它们还允许我们模拟隐藏的随机过程,并生成与真实数据相似的人工数据。
2. 给定观测值的潜在变量对参数选择 𝜃 的有效近似后验推理。这对于编码或数据表示任务很有用。
3. 变量的有效近似边际推理(Efficient approximate marginal inference)。这允许我们执行各种需要先验的推理任务。计算机视觉的常见应用包括图像去噪、上色和超分辨率(image denoising, inpainting and super - resolution)。
为了解决上述问题,我们引入一个识别模型 𝑞𝜙(𝑧|𝑥) :一个逼近难解真后验 𝑝𝜃(𝑧|𝑥) 的模型。请注意,与平均场变分推断(mean - field variational inference)中的近似后验相反,它不一定是阶乘,其参数 Φ 也不是从某种封闭形式的期望中计算出来的。相反,我们将引入一种与生成模型参数 𝜃 一起学习识别模型参数 Φ 的方法。
从编码理论的角度来看,未观察到的变量具有作为潜在表示或编码(a latent representation or code)的解释。因此,在本文中,我们也将识别模型 𝑞𝜙(𝑧|𝑥) 称为概率编码器(a probabilistic encoder),因为给定一个数据点 𝑥 ,它会在代码 𝑧 的可能值上产生一个分布(例如高斯分布),数据点 𝑥 可以从中生成。同样,我们将 𝑝𝜃(𝑥|𝑧) 称为概率解码器(a probabilistic decoder),因为给定代码,它会产生可能对应值的分布。
2.3.2 变分边界(variational bound)
边际似然(marginal likelihood)由单个数据点的边际似然之和组成 𝑙𝑜𝑔𝑝𝜃(𝑥(1),𝑥(𝑁))=∑𝑖=1𝑁𝑙𝑜𝑔𝑝𝜃(𝑥(𝑖)) ,可以分别改写为:
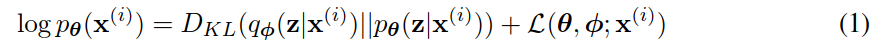
第一个最大化交叉熵(maximising cross entropy,RHS)项是近似与真实后验的KL散度。由于这个KL散度是非负的,第二个RHS项 𝐿(𝜃;𝜙;𝑥(𝑖)) 称为数据点的边际似然的(变分)下界,可以写成:
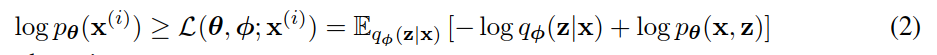
也可以写成:
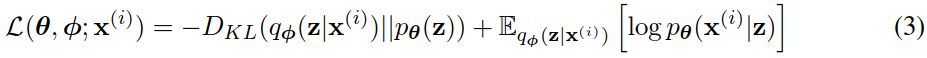
我们要对变分参数 𝜑 和生成参数 𝜃 ,求导和优化下界 𝐿(𝜃,𝜙,𝑋(𝑖)) 。然而,对 Φ 的下界梯度有点问题。对于这类问题通常的(naive)蒙特卡罗梯度估计(Monte Carlo gradient estimator)是:
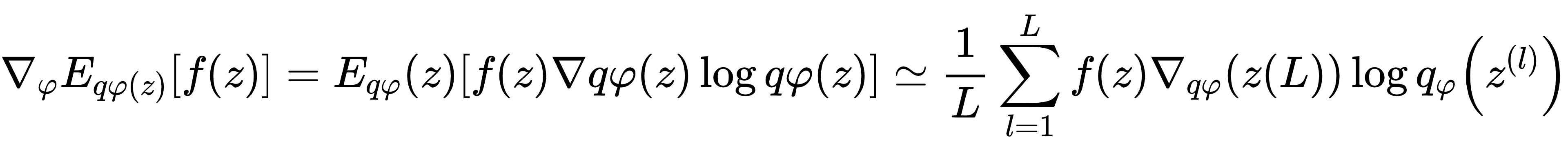
其中 𝑧(𝑙)∼𝑞𝜙(𝑧|𝑥(𝑖)) 。这个梯度估计器(gradient estimator)显示出非常高的方差(参见示例[BJP12]),对于我们的目的来说是不切实际的。

补充图2:含隐变量的参数估计。如果图模型中包含隐变量,即有部分变量是不可观测的,就需要用EM算法进行参数估计。源自邱锡鹏老师《神经网络与深度学习》。
KL散度(Kullback - Leibler Divergence),也叫KL距离或相对熵(Relative Entropy),是用概率分布 𝑞 来近似 𝑝 时所造成的信息损失量。KL散度是按照概率分布 𝑞 的最优编码对真实分布为 𝑝 的信息进行编码,其平均编码长度(即交叉熵) 𝐻(𝑝,𝑞) 和 𝑝 的最优平均编码长度(即熵) 𝐻(𝑝) 之间的差异。
2.3.3 随机梯度变分贝叶斯(SGVB)估计器和自编码变分贝叶斯(AEVB)算法
在这一节中,我们介绍了一个实用的下界估计和它的导数。我们以 𝑞𝜙(𝑧|𝑥) 的形式假设近似后验,但请注意,该技术可以应用于 𝑞𝜙(𝑧) 的情况,即我们也不以 𝑥 为条件。在附录中给出了用于推断参数后验的全变分贝叶斯方法。
在2.4节(即本文中的2.3.4节重参数化技巧)中概述的某些温和条件下,对于选择的近似后验 𝑞𝜙(𝑧|𝑥) ,我们可以使用(辅助)噪声变量的可微变换 𝑔𝜙(𝜖,𝑋) 来重参数化随机变量 𝑧~∼𝑞𝜙(𝑧|𝑥) :
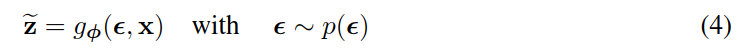
参见2.4节,选择这样一个合适的分布 𝑝(𝜖) 和函数 𝑔𝜙(𝜖,𝑥) 。我们现在可以对某个函数 𝑓(𝑧) 关于 𝜙 的期望进行蒙特卡罗估计(Monte Carlo estimates):
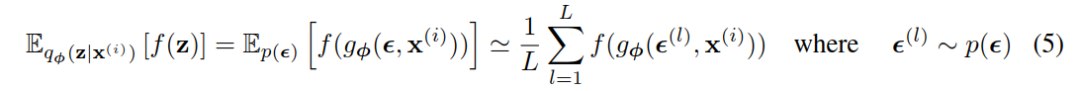
我们将这种技术应用于变分下界(variational lower bound, eq.(2)),得到我们的通用随机梯度变分贝叶斯(Stochastic Gradient Variational Bayes, SGVB)估计器 𝐿~𝐴(𝜃,𝜙;𝑥(𝑖))∼𝐿(𝜃,𝜙;𝑥(𝑖)) :
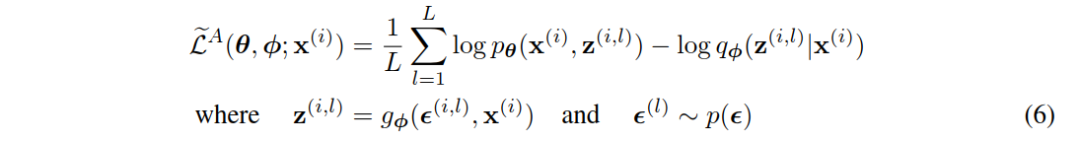
通常,eq.(3)的KL - 散度 𝐷𝐾𝐿(𝑞𝜙(𝑧|𝑥(𝑖))∥𝑝𝜃(𝑧)) 可以解析积分(见附录B),这样,只有期望的重构误差 𝐸𝑞𝜙(𝑧)log𝑝𝜃(𝑥(𝑖)|𝑧) 需要通过抽样估计。然后可以将KL - 散度解释为正则化项,鼓励近似后验接近先验 𝑝𝜃(𝑧) 。这就产生了随机梯度变分贝叶斯估计器 𝐿~𝐵(𝜃,𝜙;𝑥(𝑖)) ,对应于eq.(3),其方差通常小于一般估计量:
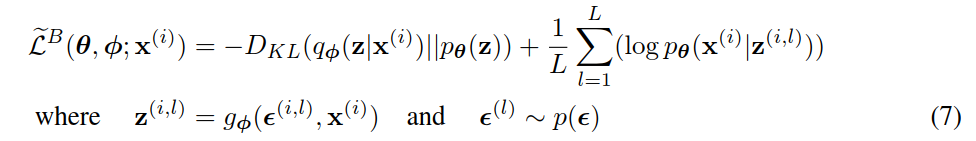
给定来自具有 𝑁 个数据点的数据集的多个数据点,我们可以基于minibatch构造完整数据集的边际似然下界(marginal likelihood lower bound)的估计量:
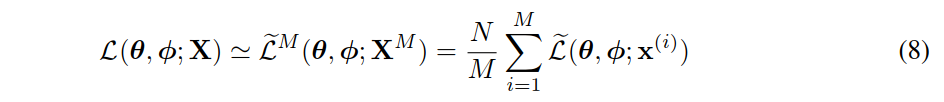
其中minibatch 𝑋𝑀={𝑥(𝑖)}𝑖=1𝑀 是从具有 𝑁 个数据点的完整数据集 𝑋 中随机抽取的 𝑀 个数据点的样本。在我们的实验中,我们发现只要小批量大小 𝑀 足够大(例如 𝑀=100 ),每个数据点的样本数量 𝐿 可以设置为1。得到的梯度 ∇𝜃,𝜙𝐿~(𝜃;𝑋𝑀) ,可以与SGD或Adagrad等随机优化方法结合使用[DHS10]。计算随机梯度的基本方法见算法1。

当查看eq.(7)给出的目标函数时,与自编码器(auto - encoders)的联系变得清晰起来。第一项是(近似后验与先验的KL散度)作为正则器,而第二项是预期的负重构误差(an expected negative reconstruction error)。选择函数 𝑔𝜙(⋅) ,它将数据点 𝑥(𝑖) 和随机噪声向量 𝜖(𝑙) 映射到该数据点的近似后验样本: 𝑧(𝑖;𝑙)=𝑔𝜙(𝜖(𝑙);𝑋(𝑖)) 其中 𝑧(𝑖,𝑙)∼𝑞𝜙(𝑧|𝑥(𝑖)) 。随后,将样本 𝑧(𝑖,𝑙) 输入到函数 log𝑝𝜃(𝑥(𝑖)|𝑧(𝑖,𝑙)) 中,该函数等于生成模型下给定 𝑧(𝑖,𝑙) 的数据点 𝑥(𝑖) 的概率密度(或质量)。这个术语是自编码器术语中的负重构错误(reconstruction error)。
2.3.4 重参数化技巧
为了解决这个问题,我们调用了另一种方法来从 𝑞𝜙(𝑧|𝑥) 生成样本。基本的参数化技巧非常简单。设 𝑧 为连续随机变量, 𝑧∼𝑞𝜙(𝑧|𝑥) 为某个条件分布。然后通常可以将随机变量表示为确定性变量 𝑧=𝑔𝜙(𝜖,𝑥) ,其中 𝜖 为具有独立边际 𝑝(𝜖) 的辅助变量, 𝑔𝜙(⋅) 为 Φ 参数化的某个向量值函数。
这种重新参数化对于我们的情况是有用的,因为它可以用来重写关于 𝑞𝜙(𝑧|𝑥) 的期望,使得期望的蒙特卡罗估计是关于 𝜙 可微的。证明如下。给定确定性映射 𝑧=𝑔𝜙(𝜖,𝑥) 我们知道 𝑞𝜙(𝑧|𝑥)𝑑𝑧=𝑝(𝜖)𝑑𝜖 。因此, ∫𝑞𝜙(𝑧|𝑥)𝑓(𝑧)𝑑𝑧=∫𝑝(𝜖)𝑓(𝑧)𝑑𝜖=∫𝑝(𝜖)𝑓(𝑔𝜙(𝜖,𝑥))𝑑𝜖 。它遵循一个可以构造可微估计量: ∫𝑞𝜙(𝑧|𝑥)𝑓(𝑧)𝑑𝑧∼1/𝐿∑𝐿=1/𝐿𝑓(𝑔𝜙(𝑥,𝜖(𝑙))) ,其中 𝜖(𝑙)∼𝑝(𝜖) 。在第2.3.3节中,我们应用这个技巧来获得变分下界的可微估计量(a differentiable estimator of the variational lower bound)。
以单变量高斯分布为例:令 𝑧∼𝑝(𝑧|𝑥)=𝑁(𝜇;𝜎2) 。在这种情况下,有效的重新参数化是 𝑧=𝜇+𝜎𝜖 ,其中 𝜖 是辅助噪声变量 𝜖∼𝑁(0,1) 。因此, 𝐸𝑁(𝑧;𝜇,𝜎2)[𝑓(𝑧)]=𝐸𝑁(𝜖;0,1)[(𝑓(𝜇+𝜎𝜖)]∼1/𝐿∑𝐿=1𝐿𝑓(𝜇+𝜎𝜖(𝐿)) ,其中 𝜖(𝐿)∼𝑁(0,1) 。
对于哪个 𝑞𝜙(𝑧|𝑥) 可以选择这样一个可微变换 𝑔𝜙(⋅) 和辅助变量 𝜖∼𝑝(𝜖) ?三种基本方法是:
1. 可处理的逆累积分布函数(CDF, Cumulative Distribution Function):在这种情况下,设 𝜖∼𝑈(0,1) ,令 𝑔𝜙(𝜖,𝑥) 是 𝑞𝜙(𝑧|𝑥) 的逆 𝐶𝐷𝐹 。例如:指数分布、柯西分布、逻辑分布、瑞利分布、帕累托分布、威布尔分布、倒数分布、Gompertz分布、Gumbel分布和Erlang分布。
2. 类似于高斯分布的例子:对于任何“位置 - 尺度(location - scale)”分布族,我们可以选择标准分布(location = 0, scale = 1)作为辅助变量,并令 𝑔(⋅)=𝑙𝑜𝑐𝑎𝑡𝑖𝑜𝑛+𝑠𝑐𝑎𝑙𝑒⋅𝜖 。例子:拉普拉斯分布、椭圆分布、Student's t分布、Logistic分布、均匀分布、三角分布和高斯分布。
3. 组合(Composition):通常可以将随机变量表示为辅助变量的不同变换。例如:对数正态分布(正态分布变量的幂)、Gamma(指数分布变量的和)、Dirichlet(Gamma变量的加权和)、Beta、Chi - Squared和F分布。
当这三种方法都失败时,对反向累计分布函数(CDF)的良好近似存在,需要与密度分布函数(PDF)相当的时间复杂度计算(参见某些方法的示例[Dev86])。
2.4 示例:变分自编码器(Variational Auto - Encoder)
在本节中,我们将给出一个示例,其中我们将神经网络用于概率编码器qϕ(z|x)(生成模型后验概率的近似pθ(x,z)),其中ϕ、θ参数使用自编码变分贝叶斯(AEVB)算法来进行联合优化。
设隐变量的先验为中心各向同性多元高斯函数pθ(z)=N(z;0,I) 。注意,在这种情况下,先验缺少参数。我们让pθ(x,z)是一个多元高斯(在实值数据的情况下)或伯努利(在二进制数据的情况下),其分布参数是用多层感知机(multilayer perceptron, MLP,一个具有单个隐藏层的全连接神经网络,见附录C)从z计算的。注意,在这种情况下,真正的后向pθ(|x)是难以处理的。虽然在qϕ(z|x)的形式中有很多自由,但我们假设真正的(但难以处理的)后验采用近似高斯形式,其协方差近似为对角。在这种情况下,我们可以让变分近似后验是一个具有对角协方差结构的多元高斯函数:
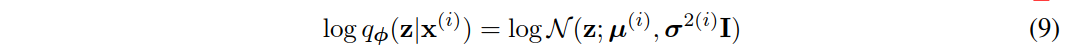
其中近似后验的均值和标准差\mu^{(i)}和σ(i)是编码多层感知机(MLP)的输出,即数据点x(i)的非线性函数和变分参数ϕ(见附录C)。
如2.4节所述,我们使用z(i,l)∼gϕ(z|x(i),ϵ(l))=μ(i)+σ(i)⊙ϵ(l),其中ϵ(l)∼N(0,I),来从后验z(i,l)∼gϕ(z|x(i))中采样。在这个模型中,pθ(z)(先验)和qϕ(z|x)都是高斯的;在这种情况下,我们可以使用eq.(7)的估计量,其中KL散度可以在不估计的情况下计算和微分(见附录B)。该模型和数据点的结果估计量为:
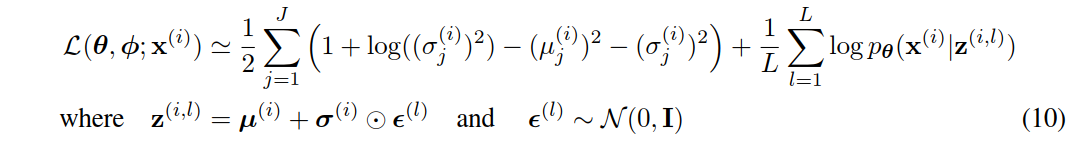
如上文和附录C所述,解码项logθ(x(i)|z(i,l))是伯努利或高斯多层感知机(MLP),具体取决于我们建模的数据类型。
2.5 相关工作
据我们所知,wake - sleep算法[HDFN95]是文献中唯一一种适用于同一类连续潜变量模型的在线学习方法。与我们的方法一样,唤醒 - 睡眠算法采用了一种近似于真实后验的识别模型。唤醒 - 睡眠算法的一个缺点是它需要同时优化两个目标函数,这两个目标函数加在一起不对应于边际似然的优化(一个界)。唤醒 - 睡眠的一个优点是它也适用于具有离散潜在变量的模型。每个数据点的Wake - Sleep计算复杂度与自编码变分贝叶斯(AEVB)相同。
随机变分推断(Stochastic variational inference)[HBWP13]最近受到越来越多的关注。最近,[BJP12]引入了一种控制变量方案来降低2.1节中讨论的naive梯度估计器的高方差,并应用于后验的指数族近似。在[RGB13]中,引入了一些一般方法,即控制变量方案,用于减小原始梯度估计量的方差。在[SK13]中,与本文中类似的再参数化被用于随机变分推断算法的有效版本中,用于学习指数族近似分布的自然参数。
自编码变分贝叶斯(AEVB)算法揭示了有向概率模型(用变分目标训练)和自动编码器之间的联系。线性自编码器与一类生成线性高斯模型之间的联系早已为人所知。[Row98]表明主成分分析(PCA)对应于线性高斯模型的一个特殊情况的最大似然(ML)解,先验p(z)=N(0;I)和条件分布p(x|z)=N(x;Wz,ϵI),特别是无穷小的情况。
最近关于自编码器的相关研究[VLL + 10]表明,非正则化自编码器(unregularized autoencoders)的训练准则对应于输入X与潜在表示z之间互信息下界的最大化(参见infomax原理[Lin89]),互信息的最大化(w.r.t.参数)等价于条件熵的最大化,条件熵的下界是自编码模型[VLL + 10]下数据的期望对数似然,即负重构误差(the negative reconstrution error)。然而,众所周知,这个重构标准本身并不足以学习有用的表示[BCV13]。已经提出了正则化技术来使自编码器学习有用的表示,例如去噪、压缩和稀疏自编码器变体(denoising, contractive and sparse autoencoder variants)[BCV13]。随机梯度变分贝叶斯(SGVB)目标包含一个由变分界决定的正则化项(例如eq.(10)),缺乏学习有用表示所需的通常令人讨厌的正则化超参数。相关的还有编码器 - 解码器架构,如预测稀疏分解(predictive sparse decomposition, PSD)[KRL08],我们从中获得了一些灵感。同样相关的还有最近引入的生成随机网络(Generative Stochastic Networks)[BTL13],其中噪声自编码器学习从数据分布中采样的马尔可夫链的转移算子。在[SL10]中,一个识别模型被用于深度玻尔兹曼机(Deep Boltzmann Machines)的有效学习。这些方法针对非规范化模型(即无向模型,如玻尔兹曼机)或仅限于稀疏编码模型,与我们提出的学习一般有向概率模型的算法形成对比。
最近提出的深度自回归网络(Deep autoregressive networks, DARN)方法[GMW13]也使用自编码结构学习有向概率模型(a directed probabilistic model),但他们的方法适用于二元隐变量(binary latent variables)。甚至最近,[RMW14]也使用我们在本文中描述的重参数化技巧将自编码器、有向概率模型和随机变分推断(auto - encoders, directed proabilistic models and stochastic variational inferenc)联系起来。他们的工作是独立于我们的,并提供了对自编码变分贝叶斯(AEVB)的额外视角。
2.6 实验
我们训练了来自MNIST和Frey Face数据集的图像生成模型,并在变分下界(variational lower bound)和估计的边际似然方面比较了学习算法。
我们使用了第3节中的生成模型(encoder,编码器)和变分近似(decoder,解码器),其中所描述的编码器和解码器具有相同数量的隐藏单元。由于Frey Face数据是连续的,我们使用了具有高斯输出的解码器,与编码器相同,只是利用解码器中的s型激活函数将平均值限制为区间(0,1)。注意,对于隐藏单元(hidden units),我们指的是编码器和解码器的神经网络的隐藏层。
采用随机梯度上升法更新参数(stochastic gradient ascent),其中梯度由微分下界估计量∇θ,ϕL(θ,ϕ;X)(见算法1),加上一个小的权重衰减项对应于先验p(θ)=N(0,I)。该目标的优化相当于近似最大后验估计(MAP)估计,其中似然梯度由下界的梯度近似。
我们比较了自编码变分贝叶斯(AEVB)与唤醒 - 睡眠算法的性能(wake - sleep algorithm)[HDFN95]。我们对唤醒 - 睡眠算法(wake - sleep algorithm)和变分自编码器采用了相同的编码器(也称为识别模型)。所有参数,包括变分参数和生成参数,通过从N(0,0.01)随机采样进行初始化,并采用最大后验估计(MAP)准则进行联合随机优化。采用Adagrad [DHS10]调整步长;根据前几次迭代在训练集上的表现,选择Adagrad的全局步长参数。使用大小为M=100的Minibatches,每个数据点L=1个样本。
2.6.1 似然下界
我们训练了生成模型(解码器)和相应的编码器(又名识别模型),在MNIST的情况下有500个隐藏单元,在Frey Face数据集的情况下有200个隐藏单元(为了防止过拟合,因为它是一个相当小的数据集)。隐藏单元数的选择是基于先前的自编码器文献,不同算法的相对性能对这些选择不太敏感。图2显示了比较下界时的结果。有趣的是,多余的潜在变量不会导致过拟合,这可以用变分界的正则化性质来解释。
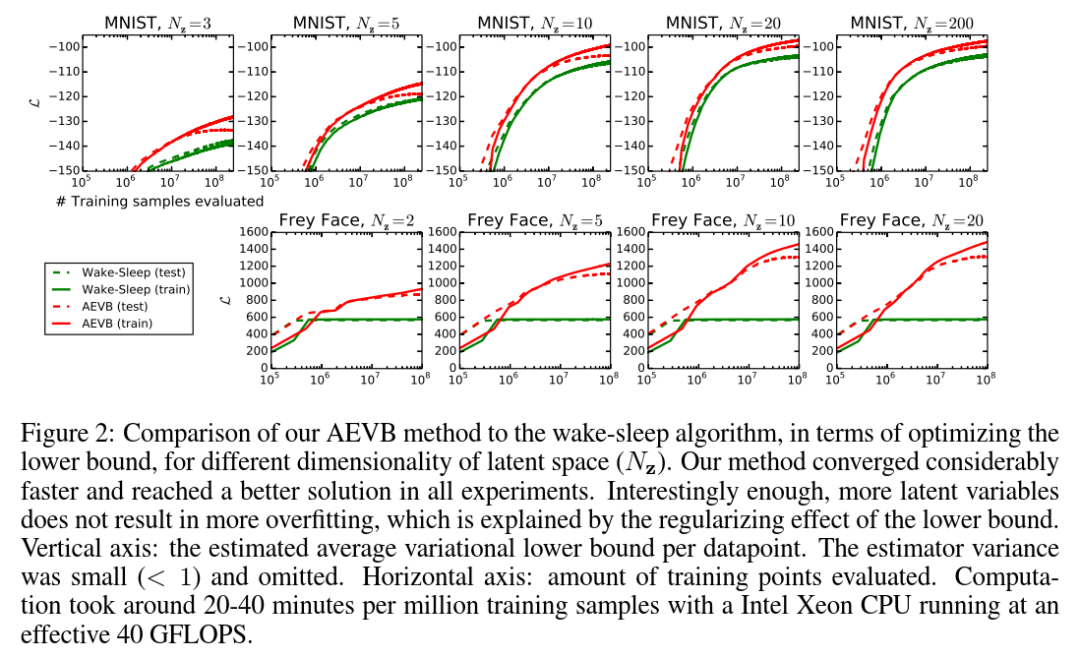
2.6.2 边际似然
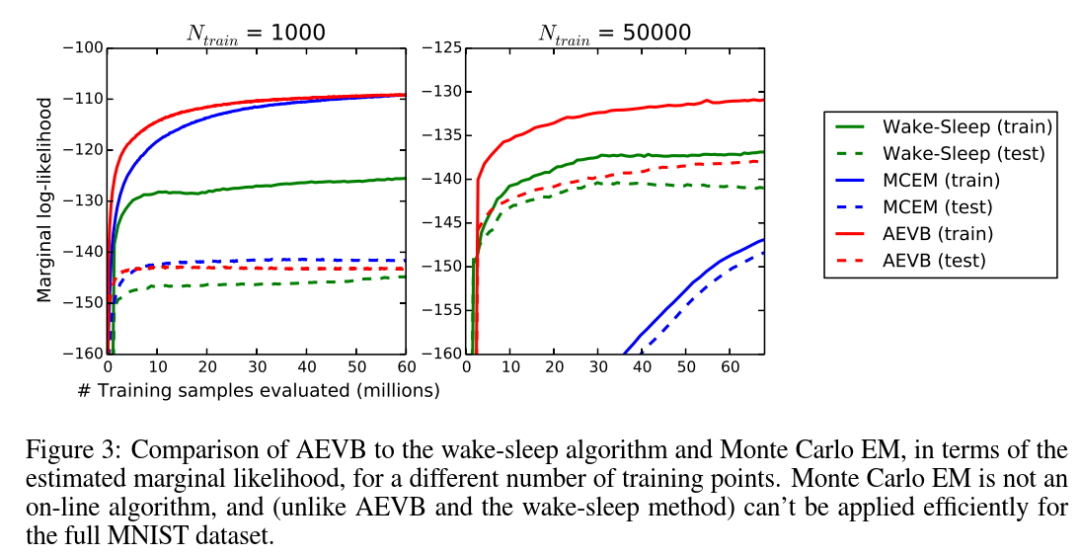
对于非常低维的潜在空间,可以使用马尔可夫链蒙特卡罗方法(MCMC)估计器估计学习生成模型的边际似然。关于边际似然估计的更多信息可在附录中找到。对于编码器和解码器,我们再次使用神经网络,这一次有100个隐藏单元和3个潜在变量;对于高维潜在空间,估计变得不可靠。同样,我们使用了MNIST数据集。采用混合蒙特卡罗(Hybrid Monte Carlo, HMC)[DKPR87]采样器将自编码变分贝叶斯(AEVB)和Wake - Sleep方法与蒙特卡罗最大似然估计(Monte Carlo Expectation Maximization, MCEM)进行比较;详情见附录。我们比较了三种算法的收敛速度,小和大的训练集大小。结果如图3所示。
2.6.3 高维数据的可视化
如果我们选择一个低维潜在空间(例如2D),我们可以使用学习到的编码器(识别模型)将高维数据投影到低维流形。参见附录A,MNIST和Frey Face数据集的二维隐流形的可视化(visualisations of the 2D latent manifolds)。
2.7 结论
我们引入了一种新的变分下界估计量,随机梯度变分贝叶斯(Stochastic Gradient Variational Bayes, SGVB),用于连续潜变量的有效近似推理。所提出的估计量可以用标准的随机梯度方法直接微分和优化。对于i.i.d数据集和每个数据点连续潜在变量的情况,我们引入了一种高效的推理和学习算法,自编码变分贝叶斯(AutoEncoding Variational Bayes, AEVB),它使用随机梯度变分贝叶斯((Stochastic Gradient Variational Bayes, SGVB)估计器学习近似推理模型。理论优势体现在实验结果上。
2.8 未来工作
由于随机梯度变分贝叶斯(SGVB)估计器和自编码变分贝叶斯(AEVB)算法几乎可以应用于任何具有连续潜变量的推理和学习问题,因此未来的发展方向有很多:
(i) 与自编码变分贝叶斯(AEVB)联合训练的编码器和解码器使用深度神经网络(例如卷积网络)学习分层生成体系结构;
(ii) 时间序列模型(即动态贝叶斯网络);
(iii) 随机梯度变分贝叶斯(SGVB)对全局参数的应用;
(iv) 带有潜在变量的监督模型,用于学习复杂的噪声分布。
本篇呈现了 VAE 的方法、示例、相关工作、实验及结论等内容。下一篇将深入解读变分自编码器(VAE)的理解,包括降维、自编码器基础、VAE 定义、正则化直觉及数学细节等内容,进一步完善对 VAE 的认知:生物医学 AI 中的变分自编码器(VAE):原理、算法与应用解析(下)。
文章改编转载自微信公众号:计算微生物组学
原文链接:https://mp.weixin.qq.com/s/jdtTYjSqV01eEeKJOHs65w?scene=1 | 








