|
在统计学的世界里,高斯分布(Gaussian Distribution)无疑是出镜率最高的“明星”。它那优美对称的钟形曲线,似乎是描绘世间万物随机性的通用语言,从测量误差、人群身高到考试成绩,无处不见其身影。
然而,当我们将目光从宏观的统计现象转向微观的物质与生命世界,尤其是当人工智能的探照灯——深度学习——射向这片领域时,另一位主角悄然登场,并占据了舞台的中心。它就是路德维希·玻尔兹曼(Ludwig Boltzmann)的传世之作:玻尔兹曼分布(Boltzmann Distribution)。
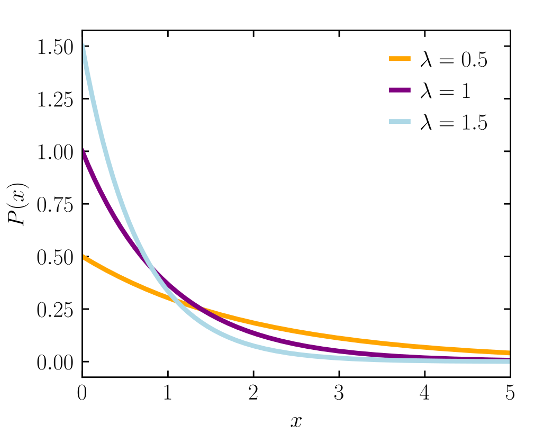
玻尔兹曼分布(图源:网络)
这并非一次简单的角色替换,而是一场深刻的“世界观”转变。高斯分布描绘的是一个围绕“平均”构建的、由大量独立随机事件累积而成的世界;而玻尔兹曼分布则揭示了一个由“能量”和“温度”主宰的、在微观粒子间不断博弈与平衡的物理世界。
当深度学习试图模拟、预测甚至设计新的材料与药物分子时,它迫切需要的,不再是统计学上的通用模板,而是一把能够指向物理真实性的“罗盘”。玻尔兹曼分布,恰好就是这把罗盘。本文将深入探讨这两大分布的本质区别,并阐明为何在探索物质与生命奥秘的征途上,深度学习与玻尔兹曼分布的结合,能够迸发出远超传统方法的强大威力。
01 双峰对峙——统计世界的两大支柱
要理解为何玻尔兹曼分布在特定领域更胜一筹,我们必须先回到源头,探寻这两大分布的诞生、它们的数学灵魂以及它们各自所统治的疆域。
第一节:曲线背后的人——数学王子与悲剧英雄
每一个伟大的科学概念背后,往往都站着一位个性鲜明的人物。高斯分布与玻尔兹曼分布的背后,正是两位在科学史上留下深刻烙印的巨匠。
卡尔·弗里德里希·高斯(Carl Friedrich Gauss, 1777-1855),被后世尊称为“数学王子”。他的才华近乎神话,据说在少年时期,老师为了打发时间让全班同学计算从1-100的加总,高斯几乎立刻就给出了正确答案5050,因为他敏锐地发现了等差数列求和的捷径。这种化繁为简的洞察力贯穿其一生。19世纪初,高斯在担任哥廷根天文台台长期间,为了处理天体观测数据中不可避免的误差,系统性地发展了最小二乘法,并在此过程中,奠定了高斯分布的理论基础。
他发现,当多次测量同一个量时,误差的分布并非完全随机,而是倾向于围绕一个中心值(真值)密集分布,且偏离越远的误差出现的概率越小。他用一个简洁优美的指数函数—— ——完美地捕捉了这一规律,这条钟形曲线也因此被冠以高斯之名。高斯分布的诞生,源于对“误差”的驯服,其内在逻辑是:在一个由众多微小、独立、随机因素共同作用的系统中,最终的结果会趋向于一个最可及的“平均态”。
而路德维希·玻尔兹曼(Ludwig Boltzmann, 1844-1906)的故事则充满了悲壮色彩。这位奥地利物理学家是统计物理学的奠基人之一,他毕生致力于用原子和分子的微观运动来解释宏观的热力学定律。在19世纪后期,原子论远未被科学界普遍接受,玻尔兹曼的理论遭到了以恩斯特·马赫(Ernst Mach)为首的实证主义哲学家的猛烈抨击,他们认为原子只是一个方便计算的假想,并非物理实在。在这场旷日持久的学术论战中,玻尔兹曼提出了他一生中最重要的贡献之一——玻尔兹曼分布。
他试图回答一个根本性问题:在一个由大量粒子组成的、处于热平衡状态的系统中(比如一杯静置的热水),粒子的能量是如何分布的?直觉上,粒子会通过碰撞不断交换能量,但最终会达到一种动态的平衡。玻尔兹曼通过精妙的统计推导指出,在这种平衡状态下,系统处于某个特定能量状态 的概率,与 成正比。这里的 是温度, 是一个基本物理常数(后被称为玻尔兹曼常数)。这个公式石破天惊,它首次将微观的粒子能量与宏观的物理量“温度”直接联系起来,揭示了温度的微观本质——即粒子平均动能的宏观体现。
玻尔兹曼长期陷于学术争论與健康困扰之中,最终于1906年9月5日去世。要注意的是,关于原子存在的理论与实验证据是在其去世前后逐步确立的:爱因斯坦在1905年提出了对布朗运动的重要理论解释,为原子论提供了关键的理论支撑,而随后让·佩兰等人在1908年前后通过实验给出了决定性的实证。将这些后来的证据回过头看,才逐渐为玻尔兹曼的统计力学思想赢得更广泛的认可。
第二节:数学的骨架——对称的钟形与单调的斜坡
从数学形式上看,高斯分布和玻尔兹曼分布的差异直观地反映了它们不同的世界观。
高斯分布的概率密度函数是:
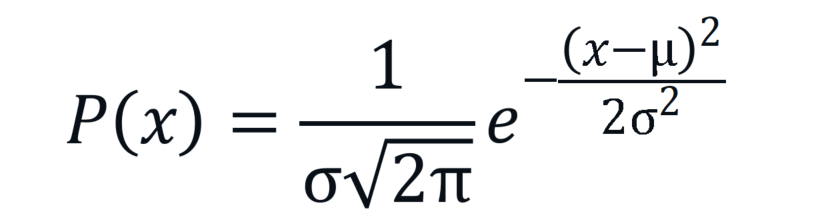
它的核心由两个参数定义:均值 和标准差。均值决定了钟形曲线的对称中心,即概率最大的位置;标准差则决定了曲线的“胖瘦”,越大,曲线越扁平,表示数据分布越分散。其关键在于二次方项,它确保了无论是大于还是小于,只要偏离的距离相同,其概率的衰减也是相同的。这是一种完美的对称性。
相比之下,玻尔兹曼分布的概率表达式通常写作:
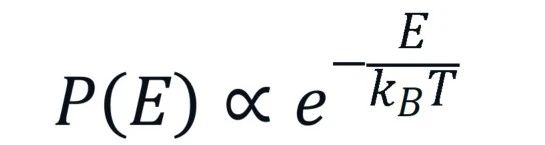
这里的“”表示“成正比于”,因为要成为严格的概率,还需要除以一个归一化因子(即配分函数),但其核心行为由指数部分主宰。它只有一个能量变量。我们立刻能发现,这个函数没有对称中心。能量越高,指数项的负值越大,概率就越小。它是一条从高到低单调递减的曲线。温度在这里扮演了调节衰减速度的角色:温度越高,分母越大,指数衰减得越慢,意味着系统有更多的机会占据高能状态;反之,温度越低,衰减越剧烈,系统几乎被“冻结”在最低能量状态。
如果用一个比喻来描绘,高斯分布就像一个宁静的圆形湖泊。湖中心(均值)的水最深(概率最高),无论你朝哪个方向、以多远的距离离开中心,水深(概率)的减小都是一样的。而玻尔兹曼分布则更像一座山的山坡。山脚(低能量)是宽阔的平地,粒子们(系统状态)最喜欢聚集在这里。随着海拔(能量)的升高,山坡变得越来越陡峭,能够爬到高处的粒子也越来越稀少。而温度 就像是登山者的体力,体力越好(温度越高),他们能达到的平均海拔就越高。
第三节:各自的舞台——普适的统计学与精准的物理学
由于其内在逻辑的不同,高斯分布和玻尔兹曼分布在现实世界中扮演着截然不同的角色。
高斯分布的普适性源于一个强大的数学定律——中心极限定理(Central Limit Theorem)。该定理指出,无论原始数据的分布形态如何,只要从其中抽取足够多的、独立的随机样本,这些样本的均值的分布就会自动趋近于高斯分布。
这一定理的威力在于,它解释了为什么高斯分布在自然界和人类社会中如此常见。
例如,一个人的身高是由成百上千个微小的遗传和环境因素共同决定的,这些因素的累积效应,最终使得人群的身高分布呈现出经典的钟形曲线。因此,高斯分布成为了实验科学、社会调查、质量控制等领域中进行统计推断和建模的基石。
而玻尔兹曼分布的舞台则更为专属,它牢牢地扎根于物理和化学世界。它的适用前提是:一个由大量粒子组成的系统,达到了热力学平衡。在此前提下,它成为了连接微观世界与宏观性质的桥梁。气体分子的速度分布(麦克斯韦-玻尔兹曼分布是其直接推论)、化学反应的平衡常数、晶体中的缺陷浓度、半导体中电子在导带的占据概率……这些看似风马牛不及的现象,其背后都遵循着同样的玻尔兹曼统计规律。
例如,空气中的氧气和氮气分子之所以没有全部沉降到地面,正是因为在室温下,它们拥有足够的动能(由温度T决定),能够克服重力势能(能量E),从而以玻尔兹曼分布所描述的概率分布在不同高度。
有趣的是,在某些特定条件下,这两个分布会发生奇妙的交汇。例如,在描述气体分子在单一方向(如x轴)上的速度分量时,其概率分布恰好是高斯分布。这是因为速度可正可负,围绕着平均速度0对称分布。
然而,当我们考虑分子的动能(与速度的平方成正比,恒为正)时,经过数学变换,其分布就变成了玻尔兹曼分布的形式。这仿佛是两位学者,一位统计学家和一位物理学家,用各自的专业语言,从不同角度描绘了同一群粒子的运动状态。
02 当深度学习拥抱物理真实
在理解了高斯与玻尔兹曼分布的本质差异后,我们便能更好地回答最初的问题:当深度学习这一强大的学习工具被应用于理解和创造物质与生命时,为什么它会天然地倾向于玻尔兹曼分布?答案在于,深度学习在此类任务中的终极目标,已经从单纯的“模式识别”转向了“物理模拟与生成”。
第四节:能量视角——为深度学习安装物理引擎
传统的监督学习任务,如图像分类,其目标是学习一个从输入(图片)到输出(标签)的映射函数。但在材料科学或药物设计中,任务往往是生成式的:给定一些化学元素,预测它们能形成何种稳定的晶体结构?给定一条氨基酸序列,它会折叠成什么样的三维蛋白质构象?
为了解决这类问题,研究人员引入了一种强大的建模框架——能量基模型(Energy-Based Models, EBMs)。其核心思想非常直观且深刻:为系统的每一种可能构型 (例如,一种特定的原子排布或蛋白质折叠形态),都通过一个深度神经网络 ,来给它分配一个标量值,我们称之为“能量”。这里的“能量”不一定严格等同于物理学中的哈密顿量,但其含义类似:能量越低,代表该构型越稳定、越“受欢迎”;能量越高,则越不稳定、越罕见。
一旦有了这个能量函数,我们就可以借助玻尔兹曼分布,将能量转化为概率:
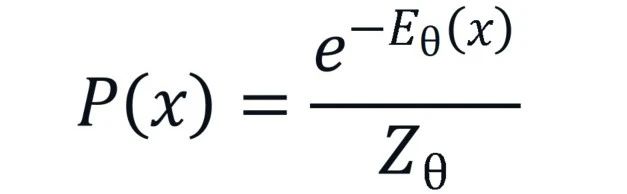
其中, 是归一化常数,被称为配分函数(Partition Function),它确保了所有可能构型的概率总和为1。通过训练神经网络(调整参数 ),使得模型学到的概率分布 与真实世界中观察到的数据分布尽可能一致,我们就相当于为深度学习安装了一个“物理引擎”。这个引擎能够理解,不同构型之间并非毫无关联,而是被一张无形的“能量地形图”所支配。
第五节:历史的回响——玻尔兹曼机与相干伊辛机
将玻尔兹曼分布与神经网络结合的想法,其实早在深度学习浪潮兴起之前就已出现。1985年,深度学习的先驱杰弗里·辛顿(Geoffrey Hinton)、特里·谢诺夫斯基(Terry Sejnowski)、大卫·阿克利(David Ackley)共同提出了一种名为玻尔兹曼机(Boltzmann Machines)的随机神经网络模型。
玻尔兹曼机由一组二元状态(0或1)的神经元构成,神经元之间通过对称的权重连接。整个网络的“能量”被定义为所有被激活的连接权重的总和。模型的精髓在于,它假设网络中单个神经元的激活状态,遵循一个局部的玻尔兹曼分布,其“能量”取决于与之相连的其他神经元的状态。
玻尔兹曼机的原始训练依赖于马尔可夫链蒙特卡洛(如 Gibbs 采样)来估计模型的期望值,这一过程计算代价高且收敛缓慢(这是早期玻尔兹曼机应用受限的原因之一)。后来对训练算法的多项改进极大地缓解了这一问题:其中最著名的是 Hinton 在 2000–2002 年间提出的对比散度(Contrastive Divergence),它把复杂的平衡态估计替换为短步的近似采样,使得受限玻尔兹曼机(RBM)及其变体在实践中可行且高效,从而推动了这类能量模型在机器学习中的复兴。
通过引入CD算法,玻尔兹曼机能够学习到训练数据中复杂的内在关联和概率分布。它不仅是深度信念网络等后续模型的理论基石,更重要的是,它首次将统计物理中处理多体系统的方法,正式引入了机器学习领域。
与此几乎同时,另一项源于物理学的优化思路——相干伊辛机(Coherent Ising Machine, CIM)——也在物理与计算交汇的边界被提出。CIM 并不是一个纯粹的算法,而是一种特殊的量子物理计算平台,它利用光学参量振荡器(Optical Parametric Oscillator, OPO)来实现对伊辛模型的模拟。伊辛模型原本是用来描述磁性材料中自旋相互作用的数学模型,但很快被发现,它能刻画许多复杂的组合优化问题,比如旅行商问题、图划分、蛋白质结构预测等。
在相干伊辛机中,每个光学参量振荡器的相位代表一个“自旋”的取向(例如 0 或 π 对应自旋向上或向下),而光学器件之间的耦合则对应伊辛模型的相互作用系数。系统从一个高噪声态开始,随着光学放大过程的进行,振荡器逐渐“锁相”,自旋配置会自发趋向最低能量的组合状态。
由于这一过程是由真实的物理演化驱动的,系统能够在并行的物理路径上同时探索大量可能解,最终收敛到近似全局最优解。这种“硬件版”的玻尔兹曼式搜索,比传统计算机在某些优化任务上更高效,尤其适合材料设计、物流调度和机器学习模型参数搜索等领域。
玻尔兹曼机和相干伊辛机,虽然一个是数学模型、一个是物理设备,但它们像两条殊途同归的溪流,都证明了玻尔兹曼分布及其衍生思想在处理复杂系统、学习数据分布和寻找全局最优解方面的强大潜力。它们的相遇不仅是计算科学与物理学的一次握手,也为后来深度学习在科学领域的跨界应用埋下了重要伏笔。
第六节:现代的复兴——为物质与生命建模
进入21世纪,随着计算能力的飞跃和深度学习技术的成熟,基于玻尔兹曼分布的生成模型迎来了复兴,并在材料与生命科学领域展现出惊人的威力。
为什么必须是玻尔兹曼分布?
物理一致性:这是最根本的原因。无论是晶体生长、蛋白质折叠还是分子间相互作用,这些过程的底层驱动力都是系统向着自由能最低的状态演化。在热平衡下,各种可能状态的统计分布,天然就符合玻尔兹曼分布。因此,当深度学习模型采用玻尔兹曼分布时,它不再是一个黑箱的模式拟合器,而是变成了一个能够理解并遵循基本物理化学定律的、具有可解释性的模拟器。它是在用物理学家和化学家的“母语”与问题直接对话。
采样效率与焦点:科学研究所关心的,往往是那些极少数的、具有特定功能的构型——例如,最稳定的材料相、具有生物活性的蛋白质折叠态、或是能与靶点紧密结合的药物分子。这些构型无一例外,都对应于能量地形图上的深邃“山谷”(低能区)。
高斯分布在此处则显得力不从心。如果用高斯分布来描述构象空间,它会假设存在一个“平均”构象,并且大部分构象都围绕它对称分布。这与现实严重不符——高能的、无意义的构象在数量上是压倒性的,而有意义的低能构象则像散落在广阔沙漠中的几片绿洲,极其稀疏。
此时,玻尔兹曼分布的优势尽显。它的指数衰减特性 意味着,概率将高度集中在低能量区域。基于玻尔兹曼分布的采样算法(如马尔可夫链蒙特卡洛,MCMC),其行为就像一个聪明的“寻宝猎人”,它不会在贫瘠的沙漠中浪费时间,而是会本能地、高效地在那些可能藏有宝藏的“绿洲”附近进行精细搜索。这极大地提升了计算效率,使得在天文数字般的可能性中找到正确答案成为可能。
应用实例:从设计新材料到破解蛋白质密码
材料科学:在预测新型合金的相图时,研究者可以构建一个能量模型,计算出成千上万种不同元素配比和原子排列的能量。然后,利用基于玻尔兹曼分布的蒙特卡洛模拟,就可以在不同温度下对这些构型进行采样,从而预测出材料在冷却过程中会经历何种相变,最终形成何种稳定的晶体结构。这大大加速了新材料的发现进程。
生命科学:蛋白质折叠问题是生物学领域的“圣杯”之一。尽管DeepMind的AlphaFold2在结构预测上取得了巨大成功,其核心并非直接的能量模型,但其训练出的“势函数”在功能上与能量函数异曲同工,都在引导搜索朝向更“合理”的构象。与此同时,另一类被称为玻尔兹曼生成器(Boltzmann Generators)的前沿模型,则更加彻底地贯彻了物理思想。这类模型由德国科学家弗兰克·诺埃(Frank Noé)等人于2019年提出,它利用一种名为“归一化流”的深度学习技术,能够直接学习并采样一个复杂体系(如蛋白质)的完整玻尔兹曼分布。这不仅能预测最稳定的结构,还能揭示蛋白质在不同构象之间动态跳变的路径和概率,为理解其生物学功能和设计药物提供了前所未有的工具。
从统计模仿到物理洞察的飞跃
回顾这场关于分布选择的讨论,我们可以得出一个清晰的结论。高斯分布,作为统计学的基石,是描述大量独立随机因素累积效应的完美工具,它代表了一种“平均化”和“对称化”的世界观。然而,当深度学习的触角伸向由能量法则支配的物质与生命世界时,这种世界观便显得“水土不服”。
玻尔兹曼分布的胜出,并非数学上的胜利,而是物理真实性的胜利。它为深度学习模型提供了一个符合第一性原理的框架,使其能够从单纯的数据驱动的模式识别,进化为基于物理洞察的生成与模拟。这种转变意义非凡:AI不再仅仅是“看到”了蛋白质的样子,而是开始“理解”为什么蛋白质会是这个样子;它不再仅仅是“记住”了哪些材料稳定,而是开始“推断”出可能存在哪些我们尚未发现的稳定材料。
需要强调的是:并不是在任何建模场景下玻尔兹曼分布都“优于”高斯;关键在于问题的物理假设——若问题由大量独立、微小的随机扰动叠加(且满足中心极限定理的条件),高斯是自然且强大的选择;但若问题的本质由能量势与热平衡主导(如材料相、分子构象的热力学分布),玻尔兹曼分布才是更合适的“物理语言”。(关于中心极限定理和高斯的适用条件,可参见经典概率论教材。)
从某种意义上说,高斯分布是数学家写给世界的通用“便笺”,简洁而普适;而玻尔兹曼分布则是物理学家破译自然奥秘的“密码本”,精准而深刻。深度学习与玻尔兹曼分布的联姻,标志着人工智能正在从一个聪明的“统计学家”,成长为一位富有洞见的“物理学家”,开启了其在基础科学发现领域中激动人心的全新篇章。
参考文献(APA 7th Edition):
Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines. Cognitive Science, 9(1), 147–169. https://doi.org/10.1016/S0364-0213(85)80012-4
Boltzmann, L. (1872). Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, 66, 275–370.
Feller, W. (1968). An introduction to probability theory and its applications (Vol. 1, 3rd ed.). Wiley.
Frenkel, D., & Smit, B. (2002). Understanding molecular simulation: From algorithms to applications (2nd ed.). Academic Press.
Gauss, C. F. (1809). Theoria motus corporum coelestium in sectionibus conicis solem ambientium. Hamburg: Friedrich Perthes and I.H. Besser.
Jaynes, E. T. (1957). Information theory and statistical mechanics. Physical Review, 106(4), 620–630. https://doi.org/10.1103/PhysRev.106.620
Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., ... & Hassabis, D. (2021). Highly accurate protein structure prediction with AlphaFold. Nature, 596(7873), 583–589. https://doi.org/10.1038/s41586-021-03819-2
Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680. https://doi.org/10.1126/science.220.4598.671
Maxwell, J. C. (1860). Illustrations of the dynamical theory of gases. Philosophical Magazine, 19(124), 19–32.
Noé, F., Olsson, S., Köhler, J., & Wu, H. (2019). Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning. Science, 365(6457), eaaw1147. https://doi.org/10.1126/science.aaw1147
文章改编转载自微信公众号:量子前哨
原文链接:https://mp.weixin.qq.com/s/JhWfOdMi4bdqxtCH9sRvdw | 








