本帖最后由 哈奇一 于 2025-9-20 19:14 编辑
计算数据库的兴起使分析、预测与发现的融合成为加速合金研究的核心主题。将机器学习与合金研究相结合,已被证明对推动多种材料的进步具有重要作用,包括非晶合金、高熵合金、形状记忆合金、磁性材料、高温合金、催化剂和结构材料。美国犹他州普罗沃杨百翰大学发表在 Nature Reviews Materials 上的《 Machine learning for alloys 》综述了机器学习驱动的合金研究现状,探讨了该领域的技术路径与应用场景,并总结了理论预测与实验验证成果。

主要内容
数据生成量近年呈现爆发式增长,而机器学习提供了提取信息的关键工具:用于材料推理的软件如今已普遍普及且常可免费获取。由此,科学家们在建立基础认知、解释实验结果以及开展原子尺度建模方面的能力得到全面提升。利用机器学习模型自动提出新实验或模拟方案以实现研究自动化正日益普及。由此形成的机器驱动反馈循环——数据生成、模型再训练与预测优化——标志着材料研究范式的重大转变。
机器学习在计算合金建模中的应用涵盖从模型哈密顿量构建(model-Hamiltonian building)到数据驱动材料科学的广泛领域。前者通常聚焦于单一材料体系,需高保真表征数据;后者则通过智能检索已知结果,对大量候选材料提出广泛性问题。所有应用均依赖材料表征(机器学习领域的核心概念之一)。表征作为材料的数学描述,既可直接呈现晶体结构,亦可采用忽略诸多细节(如元素列表、成分、原子环境或连接性)的广义间接描述。理想表征应满足四大核心要求:
不变性。不满足系统所有对称性的表征(非不变)需要更多训练数据,因为模型必须通过输出学习哪些输入数据被错误地输入。
唯一性。唯一表征可确保没有任何两种材料具有相同特征。非唯一表征无法逆向生成结构,且表征中的退化性会导致机器学习函数出现错误。
稳定性。在变形稳定的表示法中,仅存在微小变形的两种材料会呈现高度相似特征。不稳定的表示法会徒增问题难度,本质上要求对不连续量进行插值。唯一性与稳定性难以兼得:许多知名表示法均不具备这两种特性。
可解释性。可解释的表示方法能向用户揭示算法预测背后的原因。可解释性有助于揭示问题的根本洞见并合理化设计原则。
作者概述了与金属合金相关的机器学习概念、方法及成果,综述分为三个部分。首先简要概述模型哈密顿量构建与数据驱动材料科学的核心概念,继而综述计算数据库、结构表征范例及描述符搜索方法,最后探讨了机器学习在冶金合金加工、力学性能(弹性、强度、延展性、硬度、韧性、堆垛缺陷、应力热点、疲劳与开裂、磨损与蠕变)及热学性能研究中的应用。
01 背景知识框架
1.1 On-lattice 模型和Off-lattice 模型
基于晶格的模型以离散方式处理构型无序合金建模问题(即原子位于固定位置,但未必属于布拉维晶格)。合金的原子结构通常可映射到单一晶格(例如面心立方晶格),其晶格点由两种或多种原子占据。这种原子排列可能形成重复模式,从而产生特定晶体结构,也可能是随机固溶体。无论哪种情况,都假设原子至少近似位于底层晶格的晶格点上。每个原子都能直接对应一个晶格点的前提通常足够现实,足以实现精确的定量预测。许多晶格模型仅考虑截断半径定义的局部环境内相互作用。它们基于离散位置的原子占据向量(如部分占据方法),生成可解释的描述符,这些描述符可与机器学习结合用于发现新材料。晶格模型具有速度快、精度高的优势,但存在无法提供作用力且仅限于单一底层晶格的局限性。构建晶格模型的方法包括聚类展开法及其前身聚类变分法。晶格模型直接计算构型熵,速度极快。它们可用于大规模蒙特卡洛模拟,以执行热力学平均值并搜索最佳结构。由于建模难度增加,振动贡献通常不包括在网格模型中。
非晶格模型将晶格模型的适用性扩展至依赖原子坐标细节的物理量,例如声子、结构相变、输运特性及比热容。与簇展开类似,许多非晶格模型将结构信息编码为局部相互作用集,但允许原子具有连续的位置分布。为晶格模型开发的概念可延伸至非晶格领域,进而将结构信息映射至多种材料特性。最常见的非晶格模型——原子间势能模型——在Born-Oppenheimer近似框架下,将势能(通常视为电子基态能)作为原子位置的函数进行预测。该函数通常被称为势能面。这些模型通过粗粒化整合电子自由度:原子间的相互作用由模拟量子力学的经典力学关系表示。与晶格模型不同,原子位置在此被显式处理。存在两类势能函数:基于物理原理的简单势能通常具有固定函数形式和可调参数(如伦纳德-琼斯势能或嵌入原子势能);以及可系统性优化的通用原子间势能(如原子位置平滑重叠势能(SOAP)或高斯近似势能、原子簇展开法及神经网络势能。符号回归方法与图网络兼具物理基础势能与系统改进势能的特性。
非晶格模型能够利用训练数据中的额外信息,例如能量的一阶和二阶导数,在某些情况下可替代簇展开法。训练过程无需结构完全松弛(如聚类展开法),显著加快了计算速度(但需注意:当使用基于未松弛结构训练的离网格模型拟合网格构型序时,必须对每个构型进行完全松弛处理,而网格模型可直接预测松弛结构的能量)。晶格模型与非晶格模型越简单,其优势越显著:通常运行速度更快、所需训练数据更少,且相较复杂模型更易于解释。鉴于现有众多非晶格模型,在精度与效率的权衡中似乎尚无绝对优胜者。
1.2 手动机器学习方法
在结构测定领域,简单的原型聚类分析很早就已应用。通过采用各元素类型的简单原子特征(如原子半径、电负性、价电子及原子环境)作为坐标,将候选材料映射至多维特征空间。具有相同晶体结构的材料往往在特征空间中聚集成簇。当材料晶体结构尚未明确时,其在结构图中与其他结构的邻近程度便成为预测依据。
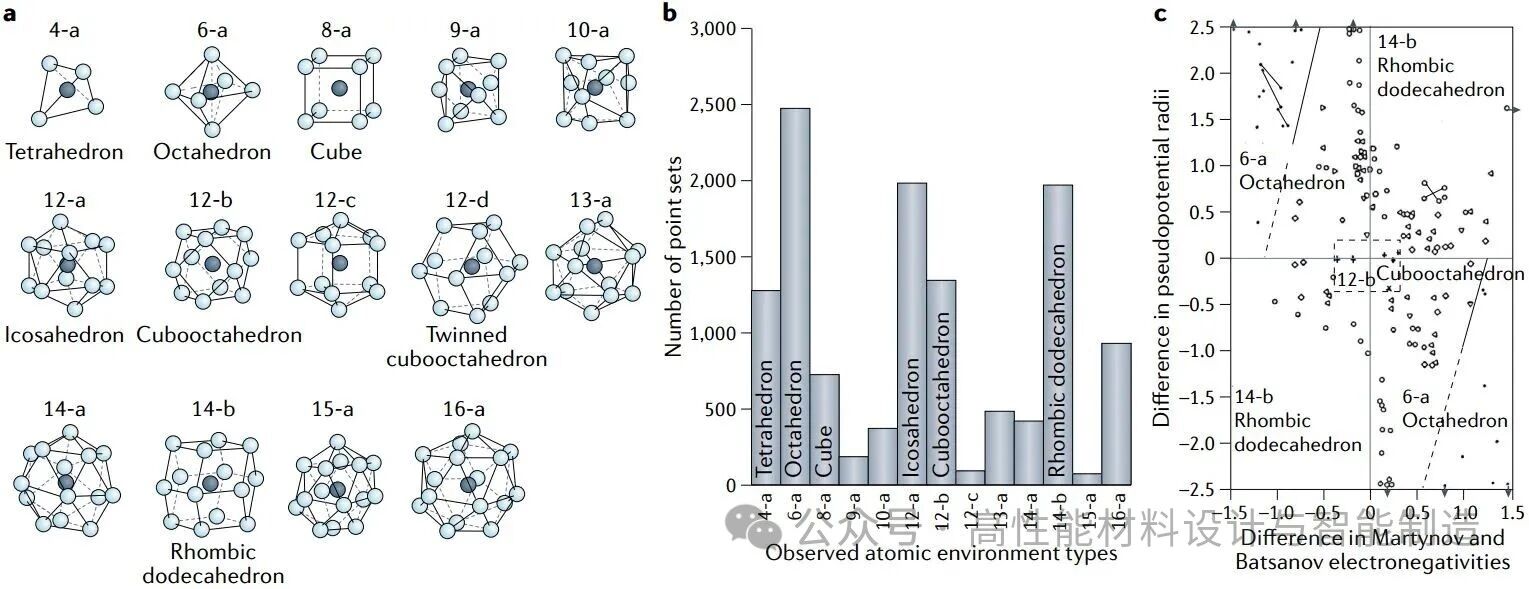
图a呈现了结构作为原子环境的现象学描述:显示了14种最常见的原子环境类型及其名称。图b展示了这14种原子环境在5,086种立方金属间化合物中的频率分布图:八面体、菱形十二面体、二十面体、立方八面体及四面体是最常见的环境结构。图c描绘了3D伪势半径与Martynov-Batsanov电负性(价电子平均电离能的平方根;该区间对应平均价电子数<2.74)的对应关系。和巴察诺夫电负性(价电子平均电离势的平方根;截面由平均价电子数<2.74给出)的3D伪势半径曲线,涵盖2,486种单环境型化合物(包括二元、三元及四元镁化物和铍化物金属间化合物)。每个符号代表一种晶体结构。
1.3 模型哈密顿量到数据驱动材料科学
原子尺度热力学建模可提供重要材料参数,前提是能量模型需具备高度精确性(许多合金构型间的能量差仅为每原子几毫电子伏特至几十毫电子伏特)且计算速度足够快以充分采样目标体系。DFT等量子力学方法虽精确且具有普适性,但常因运算速度过慢而难以计算有限温度下的热力学平均值。为此提出了替代模型方案。金属合金对计算建模构成特殊挑战,因其易形成无序固溶体,且需准确考虑构型熵效应。该问题已通过晶格模型方法(如簇展开)和离格模型方法(如高斯近似势能、原子簇展开)成功解决。两种方法均可生成可解释的模型表征。集群展开法为机器学习在材料领域的应用提供了早期验证平台,因此早期机器学习模型哈密顿量研究多集中于合金体系。
尽管替代性从头算模型能有效探究材料特异性问题,但筛选大量候选材料仍需采用不同方法。数据挖掘常与高通量计算相结合,在此情境下展现出显著效能。典型流程是采用高保真量子方法,针对海量候选材料计算目标物理量,再通过筛选结果遴选最具潜力的材料。最佳解决方案需具备实验可实现性。因此,识别所有可能的分解结构以确定全局稳定性至关重要。
1.4. 材料计算数据库
机器学习在材料科学中的应用发展,本质上与数据库的蓬勃发展密不可分——包括实验数据库(如无机晶体结构数据库)和计算数据库——以及可直接获取的描述符。后者是与可观测量相关的特征或特征组合,可用于预测复杂性质。借助高效描述符,可通过机器学习方法甚至仅凭数据挖掘技术,在数据库中搜寻新材料与特性——具体取决于最优候选方案是否已包含在计算集内。在合金理论中,形成焓(或吉布斯自由能)是衡量稳定性的典型描述符。结合簇展开技术,该方法已推动众多成功研究的开展。
选择最优聚类配置具有多种算法:交叉验证、遗传算法,甚至借鉴信号处理领域的方法,如压缩感知。除结构信息(若有)外,合金通常通过特征向量表示,其中包含成分数据,常结合元素属性如元素周期表位置、电负性、价电子浓度、熔点与液相线温度、热容量、原子半径与体积、热导率与扩散系数、熔化热等。对于拉伸强度、硬度等体积力学性能模型,热处理时长与温度、淬火类型及冷加工工艺等加工条件也常作为特征纳入考量。材料本身的计算属性(如凝聚能、密度、Miedema模型混合焓、理想混合熵)结合原子结构信息,亦可用于预测难以通过计算获得的物理量,例如弹性模量。
21世纪初数据库的迅猛发展提供了强劲动力。秉承高通量组合实验技术的精神,从头算方法被应用于生成海量数据集(目前AFLOW、OQMD、Materials Project及NOMAD数据库已收录数百万次计算结果,提取出数亿项物性数据)。这些数据库被用于预测新型材料及/或优化物性,常配合特定描述符。例如2002年提出一种密度泛函理论演化方法,可从每单元最多含四个原子的四元面心立方与体心立方结构中筛选最稳定构型。2003年则运用主成分分析法(PCA)挖掘合金与结构原型的第一性原理库中缺失信息。该研究还利用PCA展开的特征值构建自洽热力学循环,收敛至合金凸包。同年,提出多维帕累托优化法筛选兼具低压缩性、高稳定性与低成本的合金溶液。2006年,贝叶斯参数估计法被用于从鲍林文件项目数据中预测实验二元合金的晶体结构。2011年,最大似然法被提出用于挖掘无机晶体结构数据库,通过离子置换发现新化合物。
02 结构预测实例
高效的表征对机器学习至关重要。例如,2014年研究将原子间距的平均部分径向分布函数与核脊回归相结合,成功预测了费米能级电子态密度(图1a)。基于连接性的表示方法前景广阔:N-元组(独特配位环境与边序列的直方图)在预测形成能和电子能带隙方面表现出色。基于图结构构建的神经网络(NNs)采用单元胞原子作为节点、原子连接作为边,形成局部原子环境表示(图1b)。该方法在形成能、电子能带隙、费米能级及弹性特性预测中展现出合理精度。大多数表征是局域性的,存在于实空间中,可能无法有效描述周期性系统中的性质(例如来自倒易空间色散的非局域特征)。属性标记的材料片段是包含周期性的描述符示例:将晶体结构划分为原子中心的Voronoi-Dirichlet多面体(捕捉局部环境)后,通过连接总列表构建图的邻接矩阵,从而反映周期性全局拓扑结构(图1c)。机器学习还包含用于材料设计的生成模型,例如“变分自编码器”技术(图1d)。这类数学框架由编码器与解码器两组深度网络构成:前者将数据点映射至低维连续向量空间(潜在空间),后者则将潜在向量反向映射回数据点。
除物理驱动的描述符外,机器学习的结果是一个不可穿透的黑箱,通过优化内部参数连接输入与输出。鉴于描述符可由特征组合构成,近期提出了多种方向将特征整合为(可能可解释的)泛函。从庞大的数学运算及其组合出发,可通过遗传编程或确定性优化搜索所有可构造公式的空间。前者实现随机优化,正是Michael Schmidt与Hod Lipson于2009年提出的Eureqa框架方法的核心理念(图1e)。后者则由LASSO(最小绝对收缩与选择算子)及其演化版本SISSO(确定性独立筛选与稀疏化算子)所探索(图1f)。尽管非确定性,Eureqa具备覆盖更广特征空间的优势。 LASSO和SISSO似乎更高效且偏差更小,能提供真正的优化描述符,但较高的计算成本限制了可探索特征空间的规模。
近期,研究者正尝试利用神经网络加速公式发现过程。AI Feynman项目即为一例,该项目将神经网络的预测能力与基于物理启发的启发式约束(如维数分析、多项式拟合、可分离性及平移不变性等)驱动的暴力搜索相结合,对预设特征集进行符号回归分析。该算法在重新发现已知公式方面前景广阔:未来扩展可能涵盖更复杂的函数运算(积分、导数)以及在输入数据中搜索相关特征的能力。
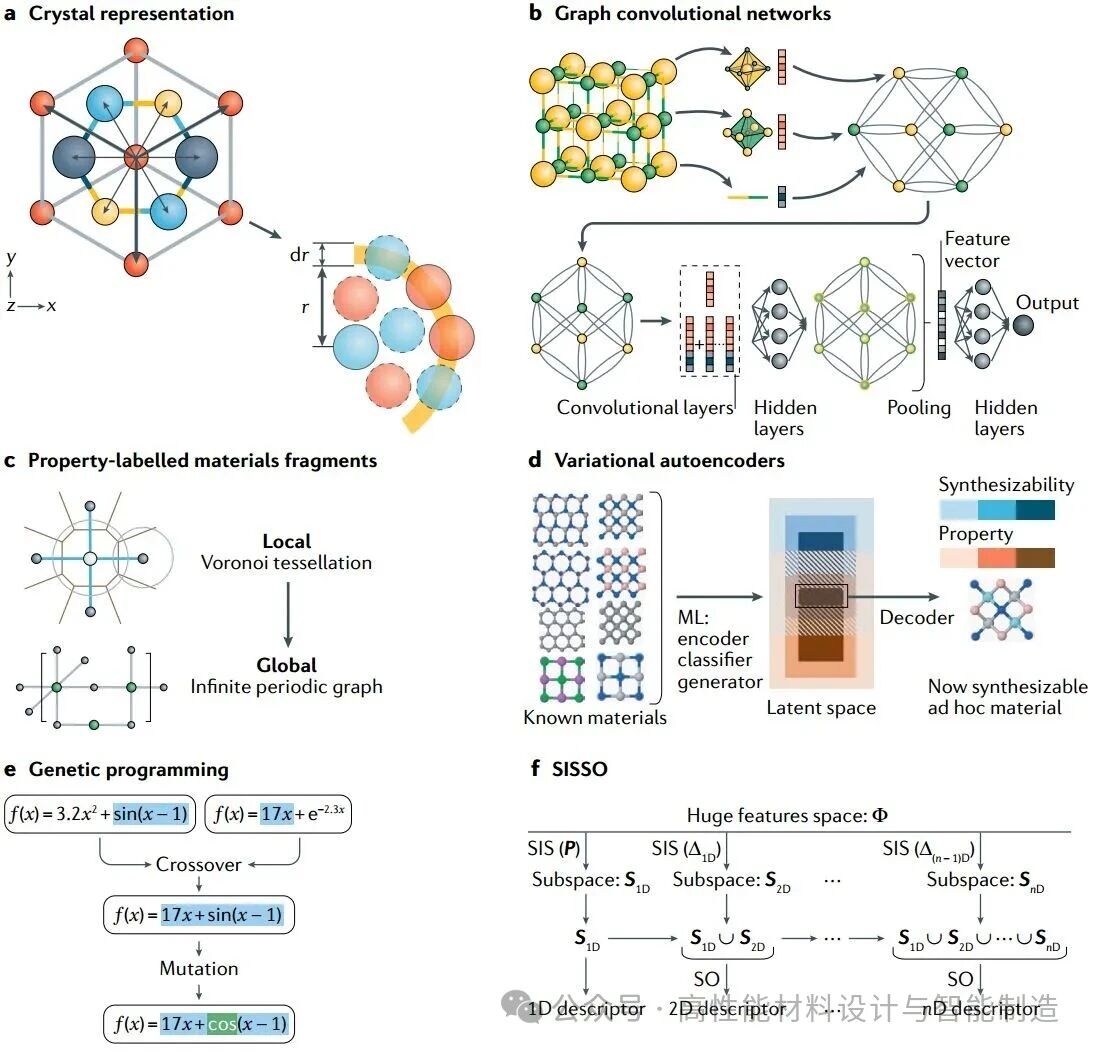
图1 | 特征选择与描述符发现的结构与方法示意图。a | 替代晶体表示法。晶胞示意图标注布拉维矢量(粗箭头)与基面(细箭头),展示“部分径向分布函数”的一层结构——该函数描述两种原子间距分布(即以另一种原子为中心、半径r、宽度dr的壳层中某类原子所占比例)。b | 晶体图卷积神经网络:晶体被转换为图结构,节点代表单位晶胞中的原子,边代表原子连接。节点与边分别由对应晶体中原子和键的向量特征描述。随后利用该图训练神经网络层生成晶体的特征向量,再通过输出层提供目标性质预测。经过首组隐藏层后,池化函数将各原子的特征整合为整个晶体的特征。c | 性质标记的材料片段包含周期性,通过连接局部Voronoi剖分与全局周期图实现。 d | 可变自编码器背后的核心思想在于:编码器将数据点映射至低维连续向量空间——即潜在空间——在此空间中进行优化(例如属性优化与可合成性优化),而解码器则将优化的潜在向量重新映射回数据点⁶⁷。e | 遗传编程中用于生成新公式的交叉与变异步骤示例,其中通过模拟自然选择的进化算法对公式进行优化。f| SISSO(确定性独立性筛选与稀疏化算子)的核心原理:通过迭代确定性优化,将确定性独立性筛选(SIS)生成的残差误差与相关性最高的统一子空间结合稀疏化算子(SO),进而提取最优描述符。循环初始阶段的目标属性P等于零维残差误差Δ0D。Δ为n维残差误差。ML指机器学习。
03 高熵合金的机器学习方法
高熵合金通常具有至少四种主要元素,可以形成单相固溶体。这种原子结构赋予了它们独特的性质,在各种技术中都有应用。例如,高熵合金在低温下表现出更好的抗断裂性,有序沉淀物的形成可以被设计为优化机械性能,如强度-延展性比。
高熵合金中的相形成已通过神经网络、高斯过程统计分析、k最近邻算法、支持向量机、主成分分析、随机森林及逻辑回归等方法进行研究。这些研究表明,价电子浓度、电负性、原子半径及混合焓均为决定相形成的关键特征。相比之下,由理想构型熵获得的混合熵被发现相对不重要,这可能是由于有限温度下的有序效应降低了材料的实际熵值。基于晶体系统和单位胞尺寸及形状的结构参数也被发现并不重要,甚至对低溶解度/低浓度体系产生反作用。
研究发现价电子浓度决定了原子堆叠特征(面心立方或体心立方)。总体而言,该方法的主要局限在于输入数据的准确性:尤其是原子半径往往定义不明确。随机森林模型被用于预测单相高熵碳化物的形成。模型基于从头算获得的高熵材料谱学描述符进行训练。预测出若干新型含铬组分;通过电弧熔炼实验合成及X射线衍射表征证实其形成单相。
遗传算法用于确定哪些特征组合与机器学习模型最能有效预测相形成。共研究70个描述符,发现模型优化在约4个描述符处趋于饱和。采用径向基核的SVM在分类固溶体形成/不形成方面表现最佳,而神经网络方法在分类固溶体类型方面效果最优。相较于LASSO、随机森林、序贯前向选择及梯度树提升等特征空间压缩方法,遗传算法表现更优。共预测出12,647种高熵合金成分:其中845种基于面心立方晶格,9,302种基于体心立方晶格,另有2,500种具有双晶相结构(体心立方/面心立方)。选取了十种分类不确定性高的化合物进行合成:其中八种形成非固溶体,一种形成体心立方相,另一种形成体心立方/面心立方双相。利用新数据(主动学习)对分类器进行重新训练,从而提高了分类准确度。
机器学习模型已被用于预测不同原子构型的能量,作为集群展开法的扩展或替代方案。基于低秩“张量列车”表示构建晶格模型的新方法,对多组分合金展现出显著优势。原子间势能基于面心立方晶格上32原子立方单元的从头算结果进行训练与验证。在AgPt、AgPtAuPd及AgPtAuPdCuNiAl合金体系中,实现了每原子3meV的验证精度。误差取决于元素在周期表中所属不同族数的数量,因为用具有相同价电子数的元素替代会产生更局部的扰动,更易通过短程原子间势能拟合。该模型经训练集(含1600种构型)验证后,可预测含多达23种元素的合金形成能,其预测误差显著低于采用压缩感知技术训练的含最近邻双元与三元项的簇展开模型。
基于机器学习的原子间势能已被用于研究高熵合金的热力学特性及力学性能。采用基于200个随机生成构型从头算结果的主动学习训练的机器学习低秩势能,对MoNbTaW合金进行了蒙特卡罗模拟。结果发现振动对形成能的贡献可忽略(每原子<0.1毫电子伏),并在约600K观测到向B2结构(Mo,W;Nb,Ta)的相变,随后在约600K分别转变为B2(Mo;Ta)和B32(Nb;W)结构。该模型对基态、半有序态和无序态的能量预测与从头算结果吻合良好,原子能偏离值分别为0.1、1.7和0.4毫电子伏。采用机器学习的原子间矩张量势能(通过矩张量描述符表征原子环境)研究了三元合金CoFeNi的晶格畸变。加热与淬火产生静态与动态畸变混合效应,导致弹性模量降低。未发现Co和Ni存在短程有序相关性,但Fe–Fe与Ni–Fe原子对呈现有序特征。
采用机器学习的“谱邻域分析势”研究了NbMoTaW中的强化机制。该势函数基于密度泛函理论计算的特殊准随机结构、基态结构和分子动力学结构组合进行训练。平衡后,铌向晶界富集,钨则在体相富集(图2e)。平衡合金强度高于随机合金,与最强元素钨相当——这归因于晶界铌富集降低了von Mises应变。
通过将机器学习模型与数据挖掘技术结合实验,研究了高熵合金的力学性能,特别是优化其硬度。采用机器学习预测与实验结果的迭代反馈流程,成功开发出Al–Co–Cr–Cu–Fe–Ni系高硬度高熵合金。径向核支持向量回归、反向传播神经网络及k最近邻算法展现出最低均方根误差。经机器学习与实验迭代验证,最终获得成分为Al45Co24Cr22Fe5Ni6的合金,其维氏硬度达865HV(8.48GPa)。引入材料描述符及剪切模量、晶格畸变能等力学特性后,交叉验证误差降至54.4HV(0.53GPa)。 最高硬度成分为Al47Co20Cr15Cu5Fe5Ni5,硬度达883HV(8.66GPa),该成分形成具有NiAl B2有序相的体心立方固溶体。
通过结合弱学习器的梯度提升树方法、从头算计算及实验测量,研究了Al0.3CoCrFeNi合金的弹性特性。夏普利加性解释表明:体积模量取决于最电子亲和力元素的电子亲和力,而剪切模量则取决于电子亲和力最弱的元素。该高熵合金即使在同种原子间也呈现出广泛的原子间距分布。尤其值得注意的是,铬-铬键距会随其他邻近原子的不同而变化,这归因于磁性相互作用,表明磁性可驱动此类体系的晶格畸变。
通过训练神经网络,在AlCoCrFeMnNi高熵合金体系中确定了硬度最高的成分组合。训练数据集包含91组通过真空电弧熔炼制备的二元至六元成分的硬度测量值。通过模拟退火法确定了最佳成分为Al₂₄Co₁₈Cr₃₅Fe₁₀Mn₇.₅Ni₅.₅的合金,其预测硬度为670±98HV (6.57±0.96GPa),实测硬度达650±12HV(6.37±0.12GPa),超越该体系文献最高值539HV(5.29GPa)。高硬度源于高铝含量形成的体心立方/B2型析出物。通过遗传算法、相图计算法(CALPHAD)、帕累托优化及数据挖掘技术组合,设计出固溶强化型体心立方合金.
基于16种元素生成成分组合,元素浓度以1%为步长从5%至35%递增。共筛选出3,155种帕累托最优合金,经选定成分实验合成与表征,维氏硬度达670±98HV(6.57±0.96GPa),而文献中该体系最高值仅为539HV(5.29GPa)。5 at%至35 at%(步长1 at%)。共发现3,155种帕累托最优合金,其中选定组分的实验合成与表征显示维氏硬度达6.45 GPa(658 HV),成为迄今报道的同等低密度金属合金中最硬的材料之一。
规范相关分析与遗传算法相结合,用于设计高熵硬质合金。输入数据包含82种体系的维氏硬度值。通过典型相关分析进行多重回归,预测体心立方或面心立方固溶体或金属间化合物的存在,并预测维氏硬度。发现硬度随理想混合熵增加而增加,随价电子浓度和混合焓降低而降低。典型相关分析用于构建遗传算法的适应度函数,在 16 种金属元素的成分空间中进行搜索。成功合成了七种预测合金:硬度范围为277HV(2.72GPa)至1,084HV(10.63GPa);其中五种合金硬度超过700HV(6.87GPa)。
04 制造工艺中的机器学习方法
监督学习算法可用于构建现象学处理-性能关系,在许多情况下其预测精度优于常用的物理近似模型。机器学习在合金领域的早期应用实例之一,是预测流动应力与温度、应变及应变率的函数关系。通过多层神经网络预测中碳钢流动应力的研究表明,其预测精度高于半经验本构模型。同期,基于Bland-Ford-Ellis模型的神经网络方法被开发用于预测钢材冷轧力。此后多个研究团队成功将神经网络方法应用于构建其他合金的加工参数与物理特性关系(例如A356铝合金的热变形行为;图4a)。神经网络方法的成功在于其灵活的曲线插值能力,能够捕捉训练数据中经验性呈现但简化物理模型难以精确描述的现象。
机器学习技术还成功应用于预测合金中相变演化与分布随加工参数的变化规律。开发出一种神经网络模型,可精确预测钛合金中α相和β相的体积分数与热处理温度及成分的关系。神经网络被用于建立钛合金的时间-温度-转变图模型,尤其针对α(六方密堆积)到β(体心立方)的相变,以预测加工-组织-性能关系。输入为化学成分,输出为时-温-变形图及马氏体始生温度。研究发现Sn、Cr和V元素可延长马氏体始生时间并降低始生温度,而Al元素则提高始生温度并缩短始生时间,Mo元素的影响则不具系统性规律。建立模型预测机械性能,包括抗拉强度、伸长率、断面缩小率、疲劳强度及断裂韧性,输入参数为成分与热处理类型。温度升高会降低抗拉强度并提高伸长率,而硬度随铝含量增加而提升。
机器学习在合金加工领域最具前景的应用之一,在于实现合金的自动化合成、加工与表征。通过将机器学习算法与机器人相结合,可构建完全自主的系统,高效开发出具有目标性能的合金。机器学习能指导后续加工条件的选取,从而大幅减少在找到最优条件前所需进行的试验次数(图4c)。同样地,通过机器学习可最小化显微镜采集样本的数量,从而加速合金微观结构的表征过程。借助计算机视觉领域的重大突破,表征工作亦可实现自动化。例如,通过训练深度卷积神经网络,可实现高碳不锈钢微观结构的自动化分割。当这些工具在自动化环境中协同运作时,有望大幅提升新型合金的设计与发现效率,并优化加工工艺条件。
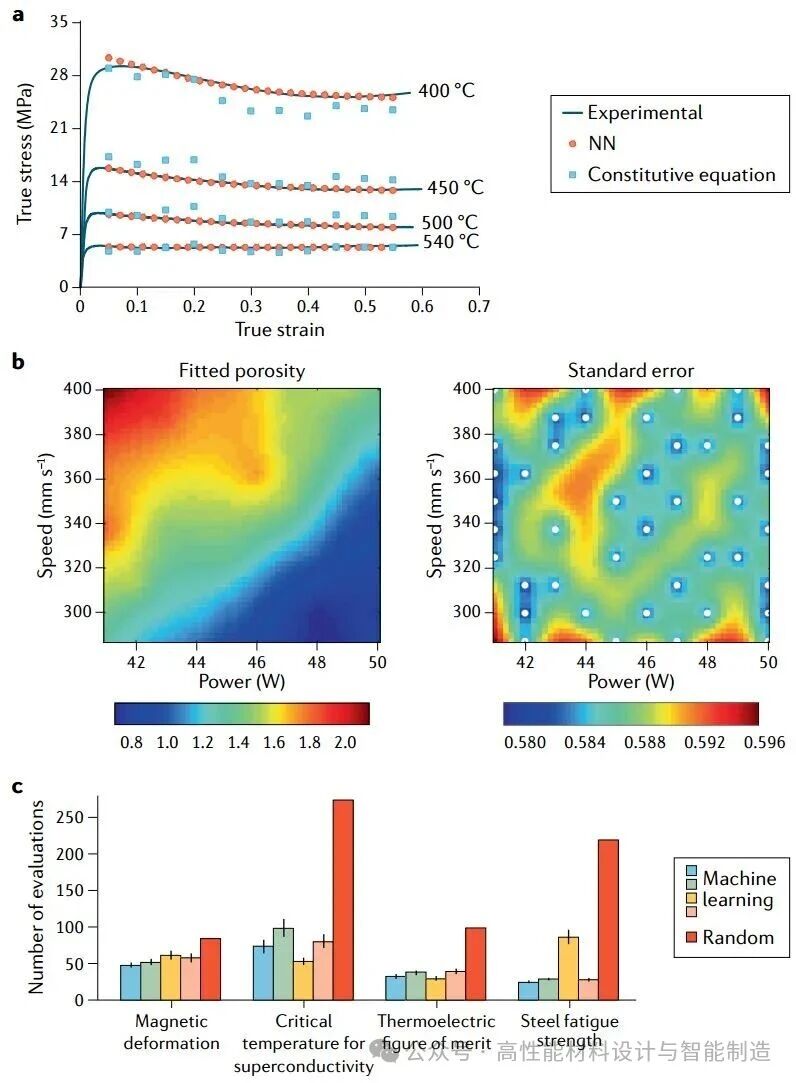
图4|合金加工的机器学习。a|在不同温度下,以每秒0.001的应变率,从神经网络(NN)模型和A356铝合金的本构方程实验获得的流动应力之间的比较。b|增材制造产生的钢材孔隙率,由仅使用初始观测值集训练的高斯过程模型预测(左)。相应的初始预测标准误差,用白点标记训练数据(右)。标准误差相对较高的地区被确定为额外采样特别有益的地区。c |与随机猜测相比,使用机器学习指导的四种方法找到不同材料特性的最佳候选者所需的试验次数(红色)。
05 机器学习预测力学性能
机器学习模型经过训练可预测金属合金的力学性能,涵盖范围从基于第一性原理计算数据训练的弹性特性通用模型,到宏观特性模型(如硬度、韧性和强度),以及特定合金体系中的磨损、疲劳、蠕变、氢脆和裂纹形成与扩展等现象。
基于密度泛函理论数据的弹性特性。基于梯度提升决策树的模型通过大型在线计算数据库进行训练,涵盖体积模量与剪切模量数据。特征参数包含组分元素的平均成分特性及实际化合物的从头算属性(如凝聚能)。最具预测价值的特征为凝聚能与单原子体积。机械性能模型可通过在线应用程序接口实现程序化访问。通过结合高斯过程建模、有限元分析、贝叶斯推断及马尔可夫链蒙特卡罗方法,从压痕测量数据推导出材料内在力学特性。该方法应用于Al 6061合金时,获得了良好的屈服应力值,但估算硬化值需更大应变量。
神经网络,k最近邻法,分类与回归树,卡方自动交互作用检测及支持向量机被训练用于预测机械性能,如抗拉强度,屈服强度伸长率, 断面缩小率,硬度,断裂韧性及冲击韧性等机械性能。研究对象涵盖钢材、铸铁、焊缝钛基合金、铜基合金、铝基合金及钼基合金的断裂韧性。输入特征包括合金成分以及加工和测试参数,如冷变形程度、时效温度和时间、热处理温度和时间、测试温,以及焊接参数,如热输入和层间温度。训练数据源自文献资料(如CASTI金属丛书、ASM手册)或通过实验合成与表征生成这些模型被用于探索成分和加工工艺对合金力学性能的影响,并结合优化算法设计出具有增强性能的新材料。一种用于预测马氏体时效钢性能的模型能够预测钴-钼相互作用对马氏体起始温度和硬度的影响,并确定C250合金的最佳成分。
该模型还预测铜元素通过促进析出相成核加速时效硬化。用于球墨铸铁与等温球墨铸铁性能分类的模型表明:添加碳化物可提升材料耐磨性,而等温球墨铸铁的延展性随奥氏体含量增加而提升;铜、锰、铬会降低强度,镍则能增强强度。基于工业数据训练的十组神经网络集合,可预测合金钢在成分与回火温度作用下的强度与延展性。通过多目标优化法寻找帕累托最优解,采用强度帕累托进化算法同时优化抗拉强度、断面缩小率、伸长率及其标准差。
采用神经网络和遗传算法设计了一种低硅含量的变形诱导塑性钢。在Fe-C-Mn-Si-Al-Mo-Cu合金体系中,除磷元素外所有元素的浓度均进行了调整,并研究了不同的处理温度。研究发现δ铁素体枝晶形成,取代异构铁素体而非保留奥氏体。通过残余奥氏体应变诱导转变为马氏体,观察到23%的均匀伸长率(无颈缩现象)。
通过将神经网络模型与优化算法结合,成功最大化焊缝的夏比冲击韧性。在改变Ni、Mn和C浓度时,线性优化器未能找到最优解,而其他方法预测的成分可获得87±20 J的韧性(实验测得值为101 J)。采用局部/混合优化器(其对成分空间的探索深度优于其他方法)调节全部13种成分浓度后,获得的成分方案具有:升高的层间温度(300°C)、-60°C下夏比韧性86±20J、室温屈服强度840±105MPa。
神经网络被用于优化钼基合金在锻模应用中的屈服应力和硬度,并通过CALPHAD/SSOL数据训练以预测相稳定性。通过最大化似然函数对优化器进行训练,使其优先改善最不优化的性能指标,并在随机游走中探索成分空间。新型合金预测屈服应力达722MPa,硬度为2.274GPa(232HV),单次循环成本为42美元,低于当前最经济合金TZC的52美元单次循环成本。
采用随机森林、线性最小二乘法、k最近邻法和神经网络回归法预测钢材的疲劳强度、断裂强度、抗拉强度和硬度,并将符号回归与遗传编程相结合,生成描述这些特性与成分和回火温度关系的方程式。随机森林最适合预测断裂强度,神经网络则适用于预测其他特性。
采用多种方法(包括RFs、SVMs和NNs)预测奥氏体钢中的堆垛错位能。该能量决定塑性变形机制:低于20mJm⁻²时呈现马氏体转变形式的转变诱导塑性;20mJm⁻²至45mJm⁻²区间表现为孪生诱导塑性;而大于45mJm⁻²时以滑移过程为主导。在堆垛缺陷能分类方面,射频识别技术略优于其他方法:其假阳性率为10%,而支持向量机或人工神经网络为13%。分类错误主要发生在低/中能区与中高能区之间,而模型在区分低/高堆垛缺陷能方面表现出极高可靠性。
更多内容详见原文。
关键术语:
Model-Hamiltonian building:通过机器学习技术构建或优化描述合金原子间相互作用的哈密顿量模型,以实现高效、准确的材料性质预测与成分设计。这一过程融合了物理建模与数据驱动方法,核心目标是平衡计算效率与预测精度,突破传统第一性原理计算(如 DFT)的高成本瓶颈。(在 Fe-Ni-Co-Al-Ta 复杂合金中 ,通过哈密顿量模型优化 L1₂和 B₂析出相的体积分数,最终设计出屈服强度 2 GPa、均匀延伸率>10% 的合金,其性能远超传统马氏体时效钢)。
布拉维晶格(Bravais Lattice):晶体学中,由无限个等同格点通过平移对称性(即格点坐标可表示为 r = n₁a₁ + n₂a₂ + n₃a₃,a₁,a₂,a₃ 为基矢,n₁,n₂,n₃ 为整数)构成的三维周期性点阵,共 14 种基本类型,是描述晶体宏观周期性的 “最小单元”。
马尔科夫链(Markov Chain):一种离散时间 / 连续时间的随机过程,核心特征是 “无后效性”(即未来状态的概率分布仅依赖于当前状态,与过去的状态无关,数学表达:P(Xₙ₊₁|Xₙ,Xₙ₋₁,…,X₁) = P(Xₙ₊₁|Xₙ))
D 伪势半径(3D Pseudopotential Radius):计算材料学中,用于简化原子实(原子核 + 内层电子)势场的参数,描述 “伪势”(替代真实原子实势场的近似势)在三维空间中的作用范围,是第一性原理计算(如密度泛函理论 DFT)的核心输入之一。
Martynov-Batsanov 电负性:电负性的一种定量标度(1980 年),用于描述原子在化学键中吸引电子的能力,计算公式为 χ = (IE + EA)/2(IE 为第一电离能,EA 为电子亲和能,单位通常为 eV),弥补了 Pauling 电负性(基于键能,无绝对数值)的局限性。
原子间距的平均部分径向分布函数(Average Partial Radial Distribution Function, 平均部分 rPDF):描述合金中 “特定原子对(如 A-A、A-B)” 在不同原子间距下的概率分布,是 “部分径向分布函数(partial rPDF)” 的统计平均值。其中:总 rPDF:描述所有原子周围的原子分布;部分 rPDF:仅针对某一类原子对(如合金中 Cu-Cu、Cu-Zn 对);平均部分 rPDF:对所有部分 rPDF 进行加权平均(权重为原子比例),反映合金的整体短程有序性。
核脊回归(Kernel Ridge Regression, KRR):结合 “核方法” 与 “脊回归” 的非线性回归算法,用于建立输入(如合金成分)与输出(如合金强度)的非线性映射,是机器学习中处理小样本、非线性问题的经典模型。
原子间矩张量势能(Atomic Cluster Expansion Potential, ACE 势):基于 “原子团簇(cluster)矩张量展开” 的多体原子间势能模型,用于描述合金中原子间的相互作用能,核心是通过 “矩张量” 量化团簇的几何特征,进而精确表征多体效应(区别于仅考虑两体作用的 Lennard-Jones 势)。
原文题目:Hart, G.L.W., Mueller, T., Toher, C. et al. Machine learning for alloys. Nat Rev Mater 6, 730–755 (2021).
原文链接: https://doi.org/10.1038/s41578-021-00340-w.
文章改编转载自微信公众号:
原文链接:https://mp.weixin.qq.com/s/DU2XKmBMx86TcEMeyFBUNw?scene=1 | 








