|
今天的案例是:STM-KNN融合模型在金融时间序列预测中的应用。
当你在预测股票价格的变化。你可以用两种思路去分析:
一种是LSTM:它就像一个善于记忆的“未来小预测家”,能记住之前价格的走势规律(比如三天前大涨,今天可能还涨),适合处理时间序列的数据。
另一种是KNN:它就像一个“查相似案例的老专家”,看到今天的情况后,会去历史中找“过去哪个时间点跟现在最像”,然后用那些时候的走势来做预测。
LSTM-KNN融合模型就是把这两个方法结合起来:
一个能记住长期趋势(LSTM),一个能查找相似历史情况(KNN)
两者一起上阵,让预测更靠谱。
核心原理
1. LSTM
LSTM 是一种改进的循环神经网络(RNN),解决了普通RNN难以记住长期信息的问题。它能有效捕捉金融时间序列中的长期依赖性。
LSTM 的核心结构包括 3 个门控机制:
输入门(Input Gate):决定当前输入有多少信息传进来。
遗忘门(Forget Gate):决定过去记忆有多少信息要丢弃。
输出门(Output Gate):决定最终输出什么内容。
LSTM 关键公式:
设:
· xt:当前输入(如某一天的价格)
· ht-1:上一时刻的隐藏状态
· Ct-1:上一时刻的记忆单元
· W,b:权重和偏置
则 LSTM 计算过程如下:
1.遗忘门:
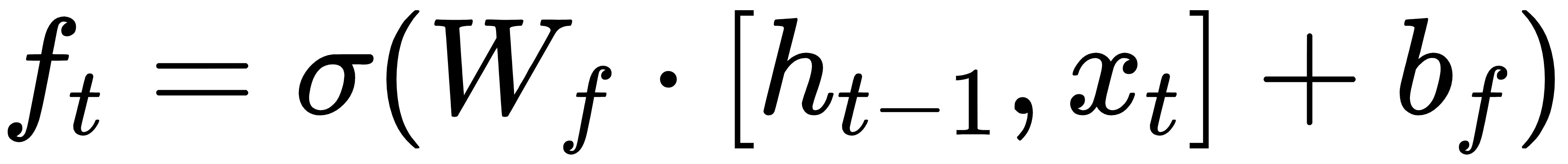
2.输入门:
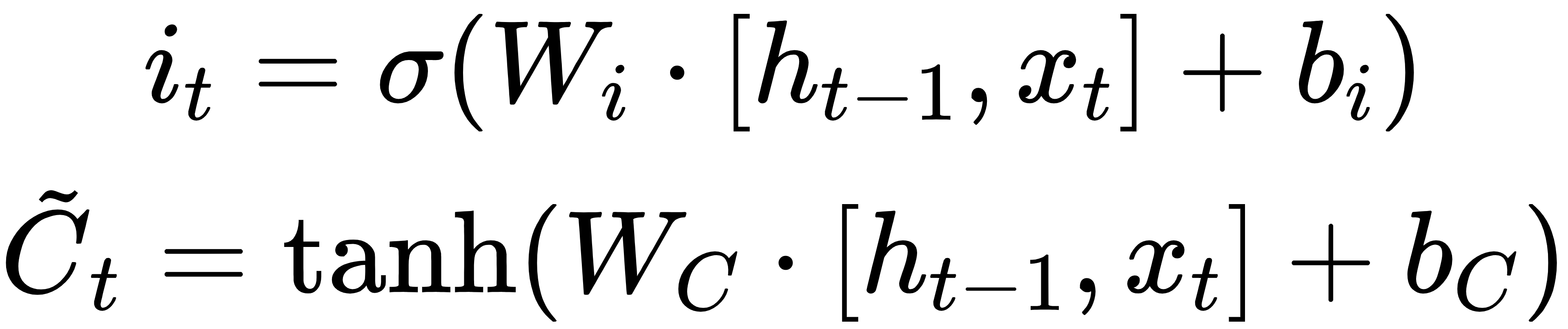
3.更新记忆单元:
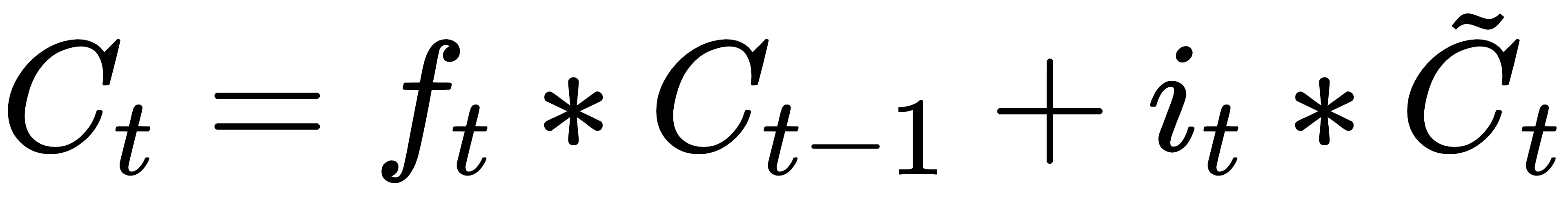
4.输出门:
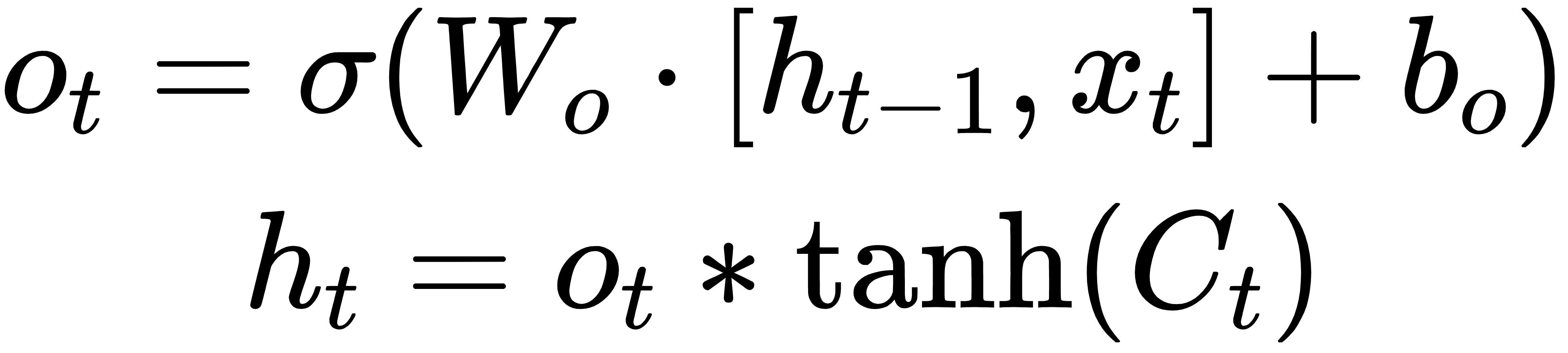
LSTM 会输出一个预测值(比如明天的价格走势),我们可以把它作为第一阶段的预测。
2. KNN(K-最近邻)
KNN 是一种基于“相似性”的非参数监督学习算法,核心思想是:
找到当前数据与历史数据中最相似的 K 个样本,看看它们的走势是涨还是跌,进行投票或加权平均。
KNN 实现步骤:
1.构造特征向量(如过去5天的涨跌)
2.定义距离度量方式(如欧式距离):
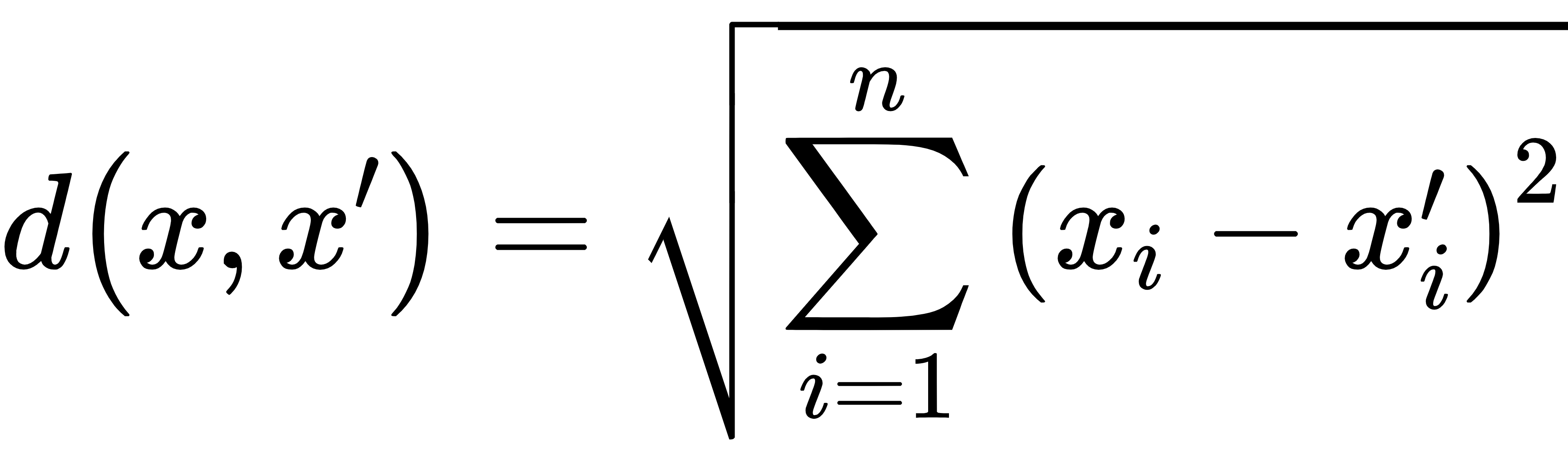
3.找到距离最近的 K 个样本
4.根据这 K 个样本的目标值(如涨跌情况)做平均或投票,得到预测值
3. LSTM-KNN 融合模型
这个融合模型可以有多种融合方式,常见的两种:
方法一:后融合(Late Fusion)
· LSTM预测值 和 KNN预测值 分别计算
· 然后做加权平均:
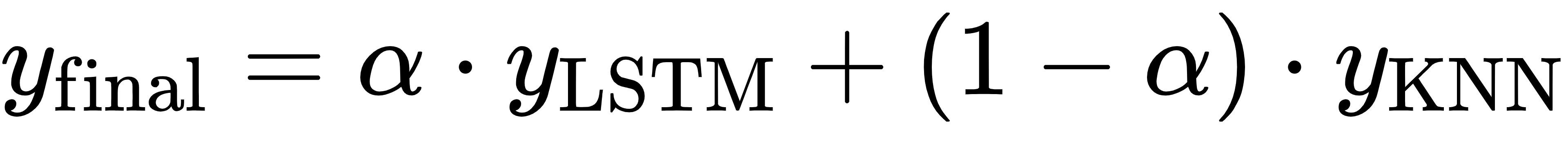
其中α∈[0,1]是融合权重
方法二:级联融合(Stacking)
· 先让 LSTM 和 KNN 各自输出结果
· 再用另一个模型(如线性回归或小型神经网络)学习如何组合这两个结果
完整案例
将LSTM(长短期记忆神经网络)和KNN(K近邻算法)相结合,用于预测金融时间序列(如股票价格)。融合的目的是同时捕捉趋势性(LSTM)和模式相似性(KNN),提升模型在波动金融数据上的预测准确性。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from sklearn.preprocessing import MinMaxScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error
from torch.utils.data import DataLoader, TensorDataset
# 1. 设定随机种子
np.random.seed(42)
torch.manual_seed(42)
# 2. 构造虚拟金融时间序列数据
days = 500
price = 100 + np.cumsum(np.random.normal(0, 1, size=days))
sma_short = pd.Series(price).rolling(5).mean()
sma_long = pd.Series(price).rolling(20).mean()
volatility = pd.Series(price).rolling(5).std()
data = pd.DataFrame({
"price": price,
"sma_short": sma_short,
"sma_long": sma_long,
"volatility": volatility
}).dropna().reset_index(drop=True)
# 3. 特征缩放与滑动窗口生成序列数据
features = ['price', 'sma_short', 'sma_long', 'volatility']
scaler = MinMaxScaler()
data_scaled = scaler.fit_transform(data[features])
def create_sequences(data, target_index=0, seq_len=20):
X, y = [], []
for i in range(len(data) - seq_len):
X.append(data[i:i+seq_len])
y.append(data[i+seq_len][target_index])
return np.array(X), np.array(y)
X_seq, y_seq = create_sequences(data_scaled, seq_len=20)
split = int(len(X_seq) * 0.8)
X_train, y_train = X_seq[:split], y_seq[:split]
X_test, y_test = X_seq[split:], y_seq[split:]
# 4. 定义 LSTM 模型结构
class LSTMModel(nn.Module):
def __init__(self, input_size, hidden_size=64, num_layers=2):
super(LSTMModel, self).__init__()
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, 1)
def forward(self, x):
out, _ = self.lstm(x)
return self.fc(out[:, -1, :])
# 5. 模型训练
model = LSTMModel(input_size=4)
loss_fn = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
X_train_t = torch.tensor(X_train, dtype=torch.float32)
y_train_t = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
X_test_t = torch.tensor(X_test, dtype=torch.float32)
train_dl = DataLoader(TensorDataset(X_train_t, y_train_t), batch_size=32, shuffle=True)
train_losses = []
for epoch in range(50):
model.train()
batch_losses = []
for xb, yb in train_dl:
optimizer.zero_grad()
pred = model(xb)
loss = loss_fn(pred, yb)
loss.backward()
optimizer.step()
batch_losses.append(loss.item())
train_losses.append(np.mean(batch_losses))
# 6. 构建 KNN 模型并预测
X_train_knn = X_train.reshape(X_train.shape[0], -1)
X_test_knn = X_test.reshape(X_test.shape[0], -1)
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(X_train_knn, y_train)
y_knn_pred = knn.predict(X_test_knn)
# 7. LSTM + KNN 融合预测
model.eval()
with torch.no_grad():
y_lstm_pred = model(X_test_t).numpy().flatten()
alpha = 0.6 # 融合比例
y_fused = alpha * y_lstm_pred + (1 - alpha) * y_knn_pred
# 8. 可视化分析
# 图1:价格与均线
plt.figure(figsize=(12, 5))
plt.plot(data['price'], label='Price', color='blue')
plt.plot(data['sma_short'], label='SMA 5', color='orange')
plt.plot(data['sma_long'], label='SMA 20', color='green')
plt.title('Price with Moving Averages')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
# 图2:训练损失曲线
plt.figure(figsize=(10, 4))
plt.plot(train_losses, color='crimson')
plt.title('Training Loss Curve (MSE)')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.grid(True)
plt.tight_layout()
plt.show()
# 图3:预测对比图
plt.figure(figsize=(14, 6))
plt.plot(y_test, label='True', color='black')
plt.plot(y_lstm_pred, label='LSTM', color='blue', linestyle='--')
plt.plot(y_knn_pred, label='KNN', color='green', linestyle=':')
plt.plot(y_fused, label='Fused', color='red')
plt.title('Prediction: True vs LSTM vs KNN vs Fused')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
# 图4:残差图
residuals = y_test - y_fused
plt.figure(figsize=(12, 4))
plt.bar(range(len(residuals)), residuals, color='orange')
plt.title('Prediction Residuals (True - Fused)')
plt.tight_layout()
plt.show()
# 9. 模型性能评估
mse = mean_squared_error(y_test, y_fused)
mae = mean_absolute_error(y_test, y_fused)
print(f"Fused Prediction MSE: {mse:.6f}")
print(f"Fused Prediction MAE: {mae:.6f}")
第一步:数据构建与预处理
· 使用 numpy 构造 500 天的“虚拟股票价格”,模拟市场波动;
· 衍生出几个基础技术指标(短期、长期均线和波动率);
· 使用 MinMaxScaler 将数据归一化到 [0, 1] 区间。
第二步:构造时间序列数据(滑动窗口)
· 用过去20 天的数据序列预测第 21 天的价格;
· 避免时间信息“穿越未来”导致数据泄露;
· 得到训练集和测试集。
第三步:定义并训练 LSTM 模型
· PyTorch 实现一个两层 LSTM 网络,捕捉时间序列的趋势;
· 损失函数为 MSE,优化器使用 Adam;
· 每轮迭代记录损失,便于绘图观察模型是否收敛。
第四步:构建 KNN 模型(基于历史相似性)
· 把序列扁平化为向量,使用KNeighborsRegressor寻找最相似的历史片段;
· 模拟“图形识别型交易系统”的逻辑。
第五步:LSTM-KNN 融合预测
· 融合策略为加权平均:
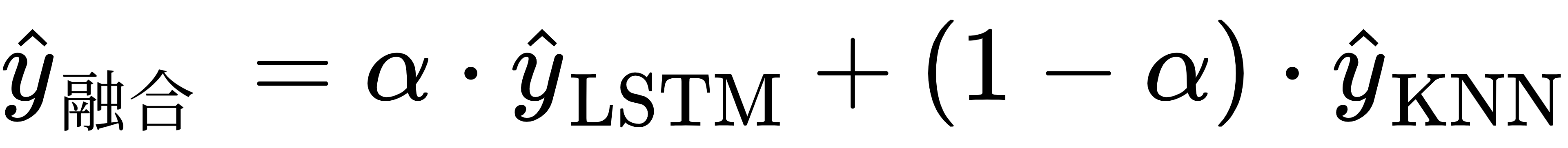
· 权重 alpha=0.6,表示更侧重 LSTM 趋势判断。
数据分析图
图1:价格与均线趋势图
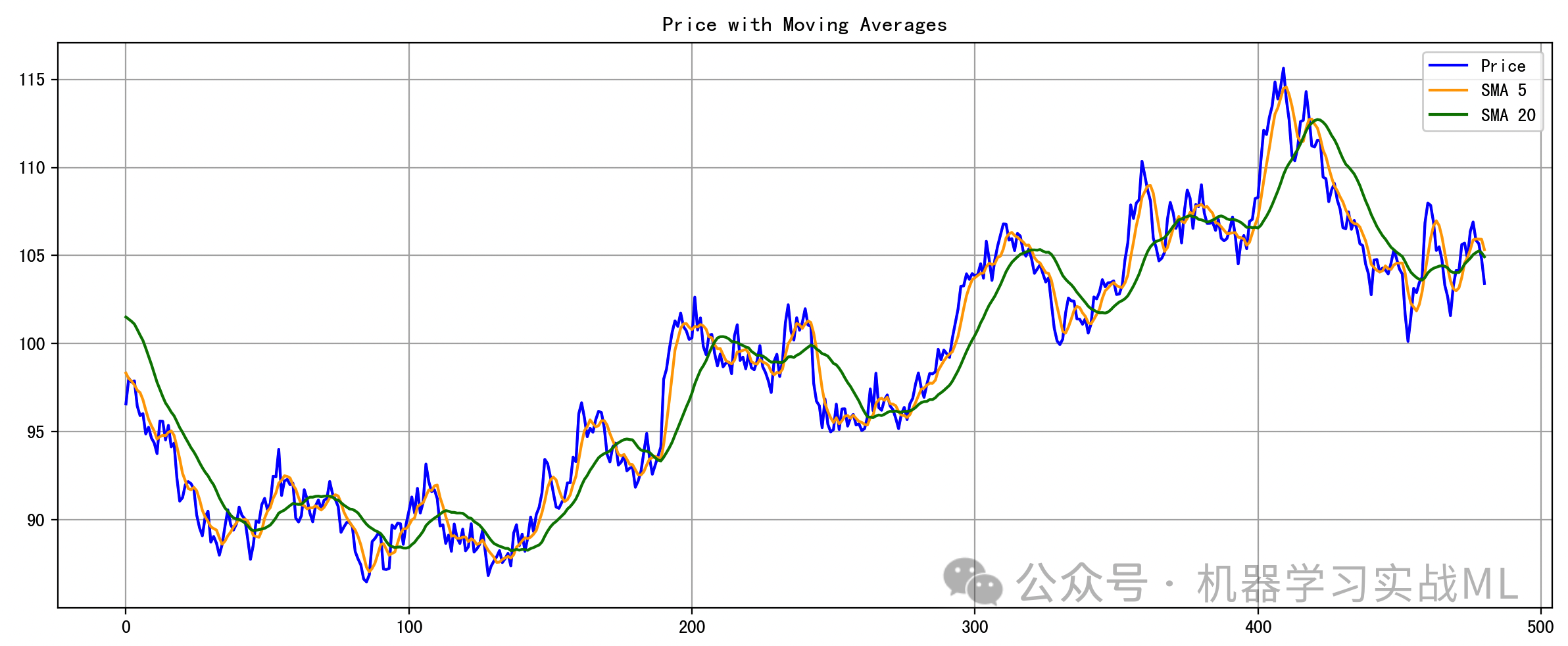
展示模拟市场价格随时间的波动情况,显示技术指标对趋势的平滑作用,LSTM 主要就是要学这种趋势结构。
图2:训练误差下降曲线
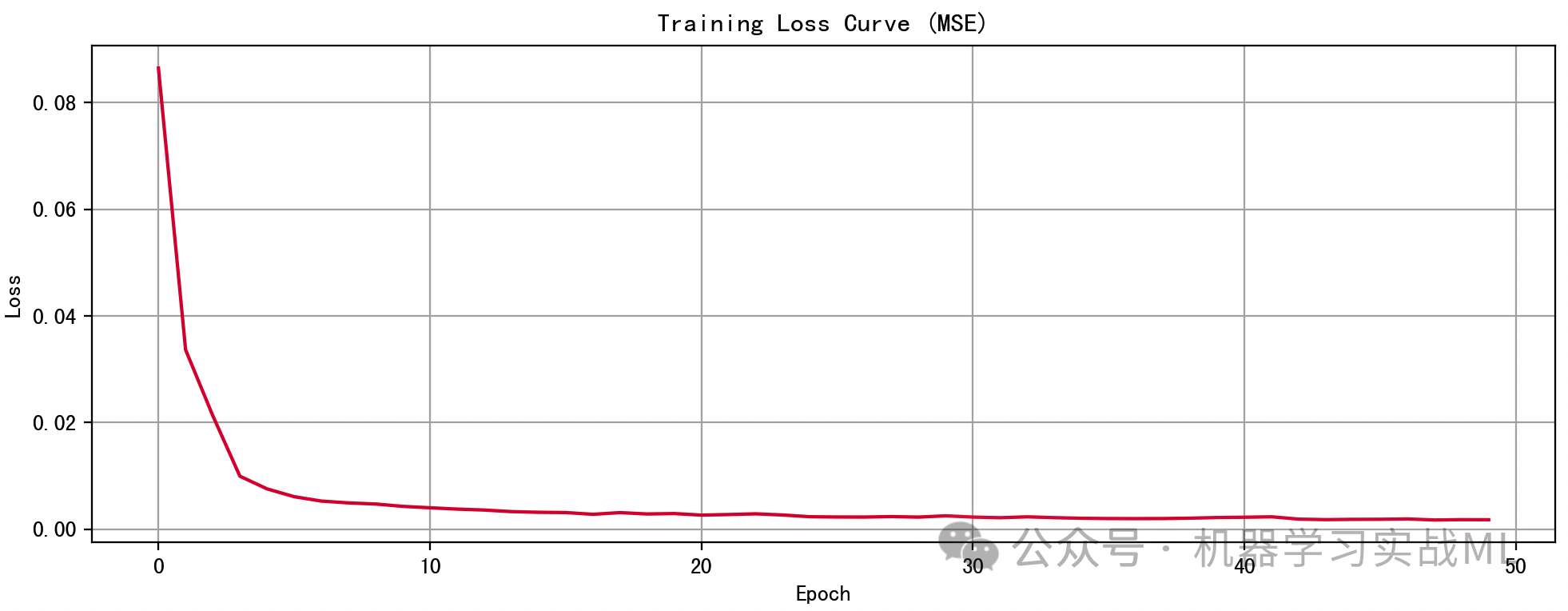
显示 LSTM 训练过程中损失逐渐减小,判断是否过拟合或欠拟合,趋势平稳下降表示模型收敛良好。
图3:真实值 vs LSTM vs KNN vs 融合预测
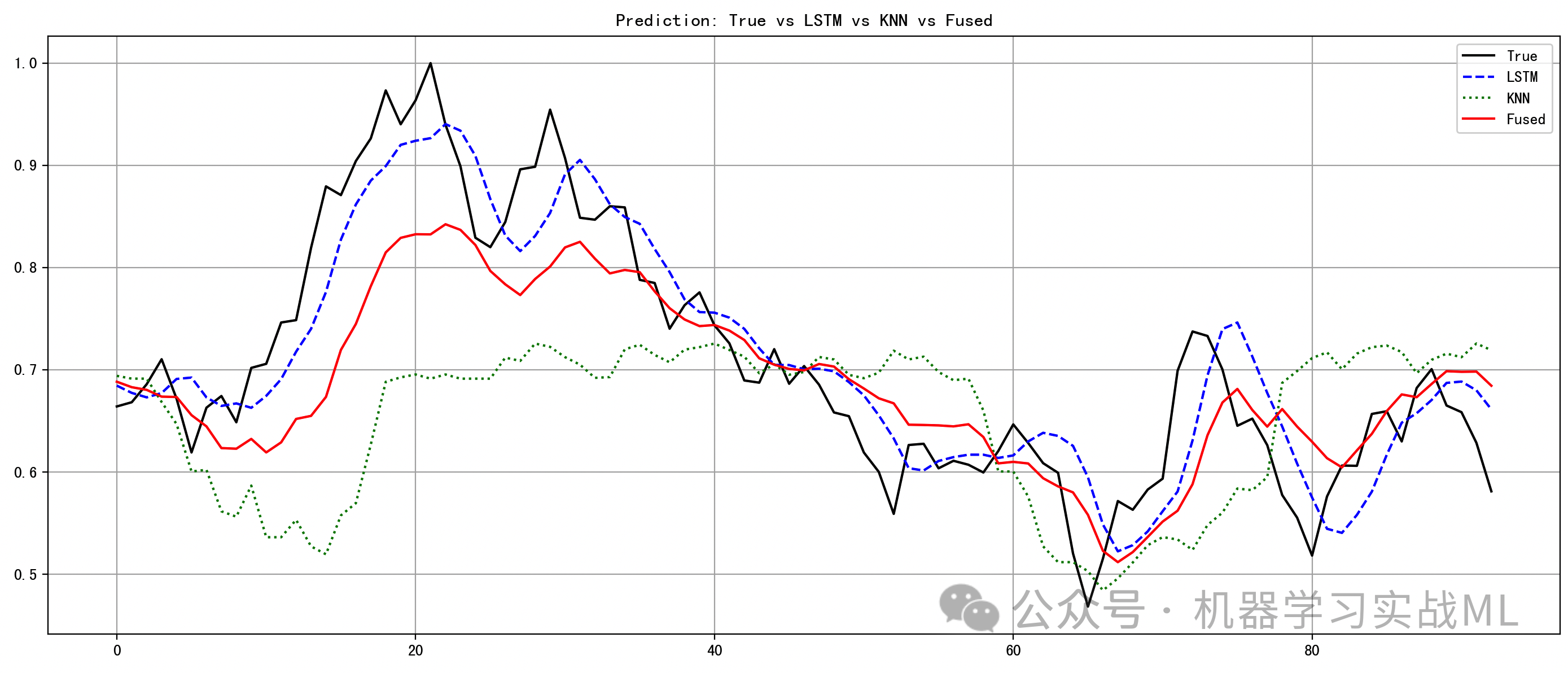
直观对比四条曲线的重合程度,融合预测(红色线)更贴近真实走势(黑线),融合能补偿 LSTM 在拐点滞后的问题,KNN则在局部震荡中表现更稳定。
图4:残差条形图(真实 - 融合预测)
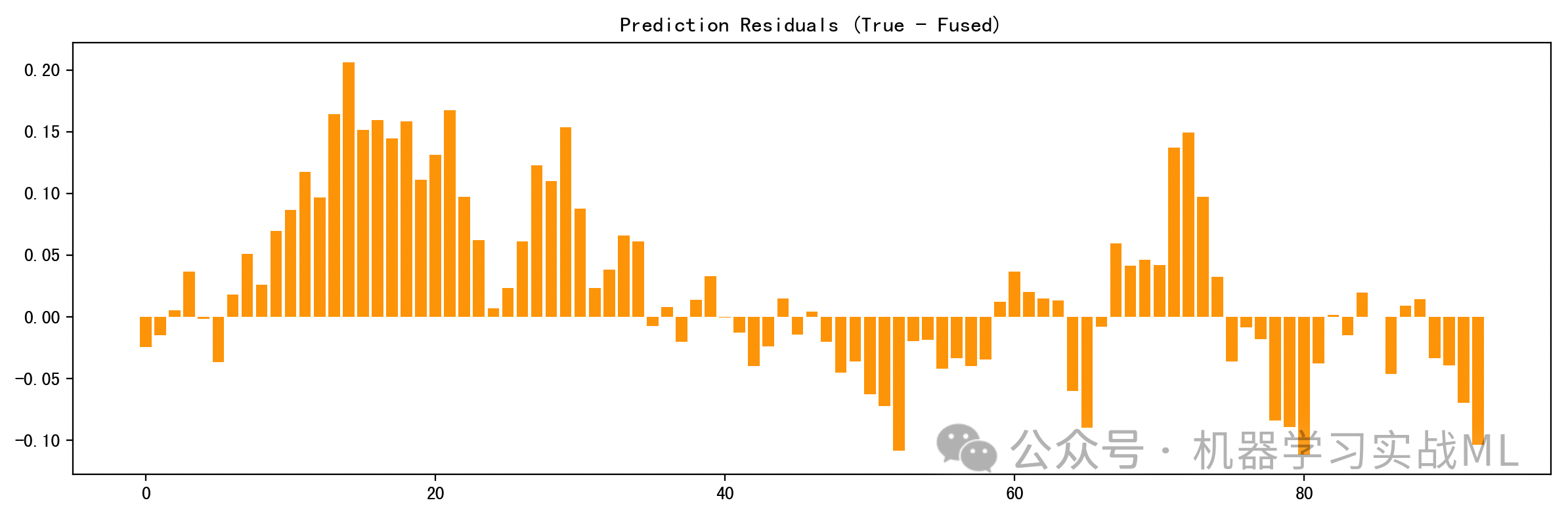
可视化每一个时间点预测误差,较小和平均分布的残差说明模型表现稳定,某些高波动时期误差增大,也反映模型挑战点。
文章改编转载自微信公众号:机器学习实战ML
原文链接:https://mp.weixin.qq.com/s/ifTlZqJKmDkuQC_2sStlpQ?scene=1 | 






















