本帖最后由 宇宙微尘 于 2026-1-6 20:50 编辑
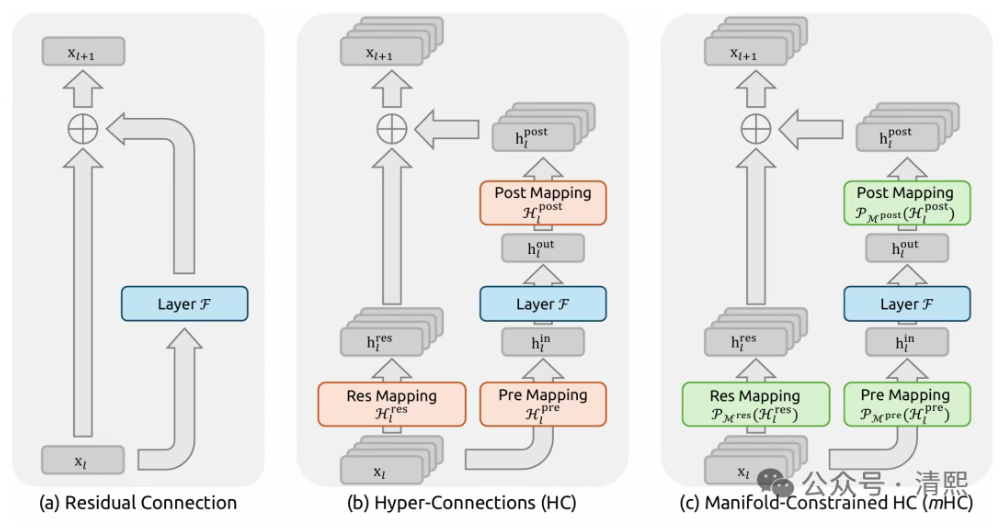
华人学者闪耀2026元旦,前有DeepSeek mHC:一次将 Transformer 残差流拉回重整化轨道的重大升级,
后有清华的“算盘:可扩展光子线性向量机”【文献1】与中科院大学的“可编程光子Ising机”【文献2】双双登上Nature。
Ising 机 - Nature 灌水机 中,笔者总结,过去几年,人工智能的进步几乎被简化为一条路径:堆 GPU、堆数据、堆参数。
Transformer 正是这一范式的巅峰,将大规模线性代数、统计建模和工程可扩展性结合在一起,构成了当今 AI 的通用骨架。
但在这种高度成功的范式中,一个更深层的问题开始隐现:
当问题从“表征与生成”转向“选择与决策”,Transformer 的计算逻辑正在变得低效。这不是工程问题,而是计算本身的结构问题。
Transformer 能力边界
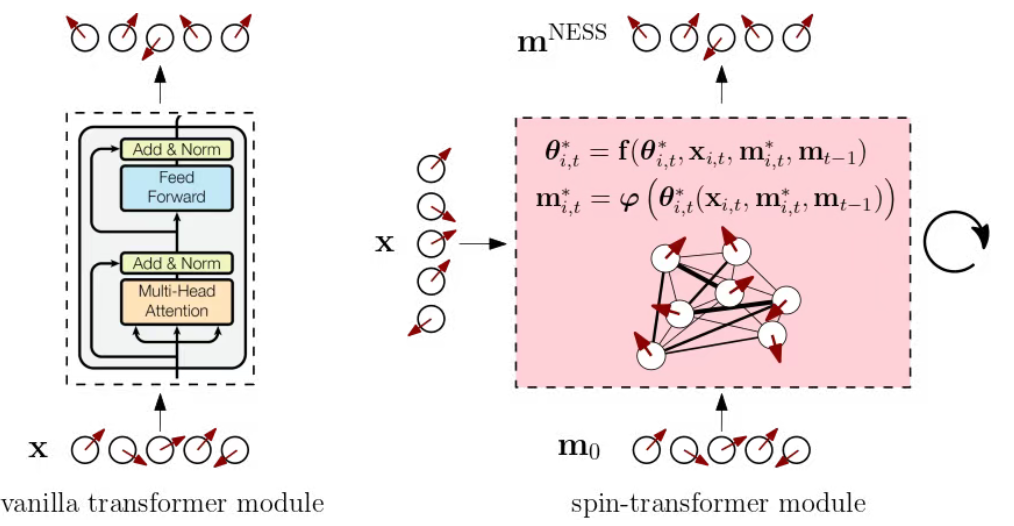
从本质上看,Transformer 是一个高度成熟的表征学习系统,
擅长在连续、高维、可微的空间中,通过线性变换和注意力机制,建模“可能、合理、概率较高”的米田嵌入。
然而当问题具有强约束、离散决策、多解选择和全局一致性要求时,难点不在于表征是否丰富,而在如何从庞大的可选空间中搜索最佳选择。
Transformer 不是不能处理这类问题,而是只能通过很昂贵的方式来近似,堆参数、拉上下文、反复采样。
而这常被误解为“规模仍然不够”,其实更准确的理解是,表征学习并不是决策搜索的自然方式。
搜索是个物理问题
这正是 Ising 模型反复出现在计算领域的原因,不是因为“古老”或“优雅”,而是抓住了搜索问题的最小物理结构。
Ising 系统并不执行算法步骤,而是将离散变量和约束编码为一个能量函数,让系统通过自身动力学演化,收敛到稳定态。
所以,解不是被“算出来”的,而是在竞争、耦合和涨落中被自然选出来的。
在数字计算中,决策搜索复杂度体现为时间和步骤数;而在 Ising 系统中,搜索复杂度体现为能量景观和相变结构。
也就是说,复杂性并没有被消除,而是被转移给了物理系统本身。
计算范式的转向
清华和中科院大学元旦这两项 Nature研究,从不同侧面证明了这种计算范式的现实性。
可编程光子 Ising 机【文献2】已经能够在室温下稳定运行,并被直接用于真实交通优化问题,在解的质量和效率上超越传统方法。这意味着组合优化正在脱离通用数字计算,走向专用物理系统。
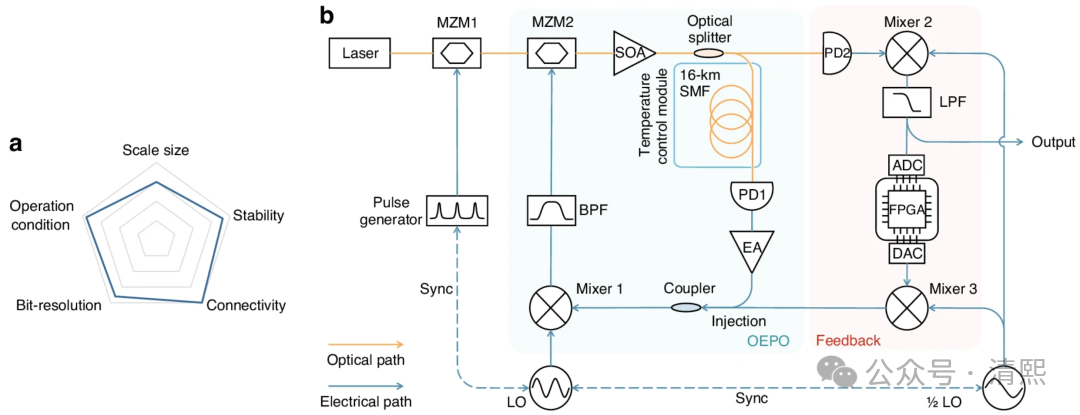
OEIM性能雷达图和实验设置
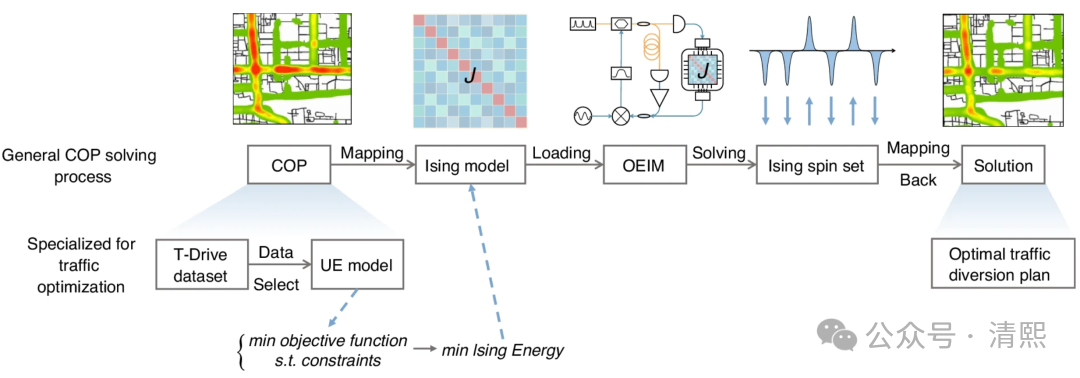
一般COP和流量优化问题的求解过程
算盘光子线性向量机【文献1】展示了一种极其简洁、可扩展的光子线性代数架构,将 AI 中最昂贵的线性算子直接交由物理过程完成,绕开了冯·诺依曼瓶颈。
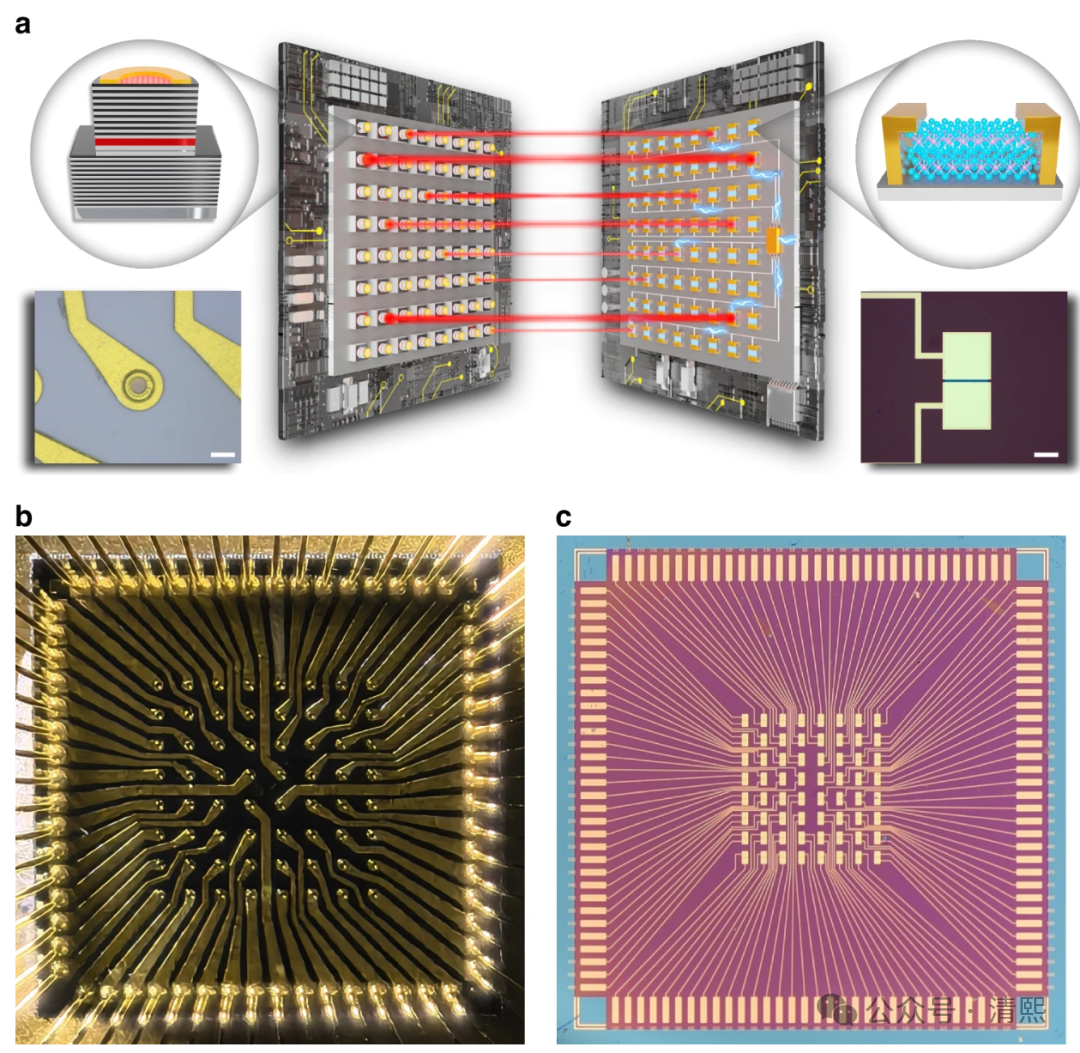
SUANPAN架构
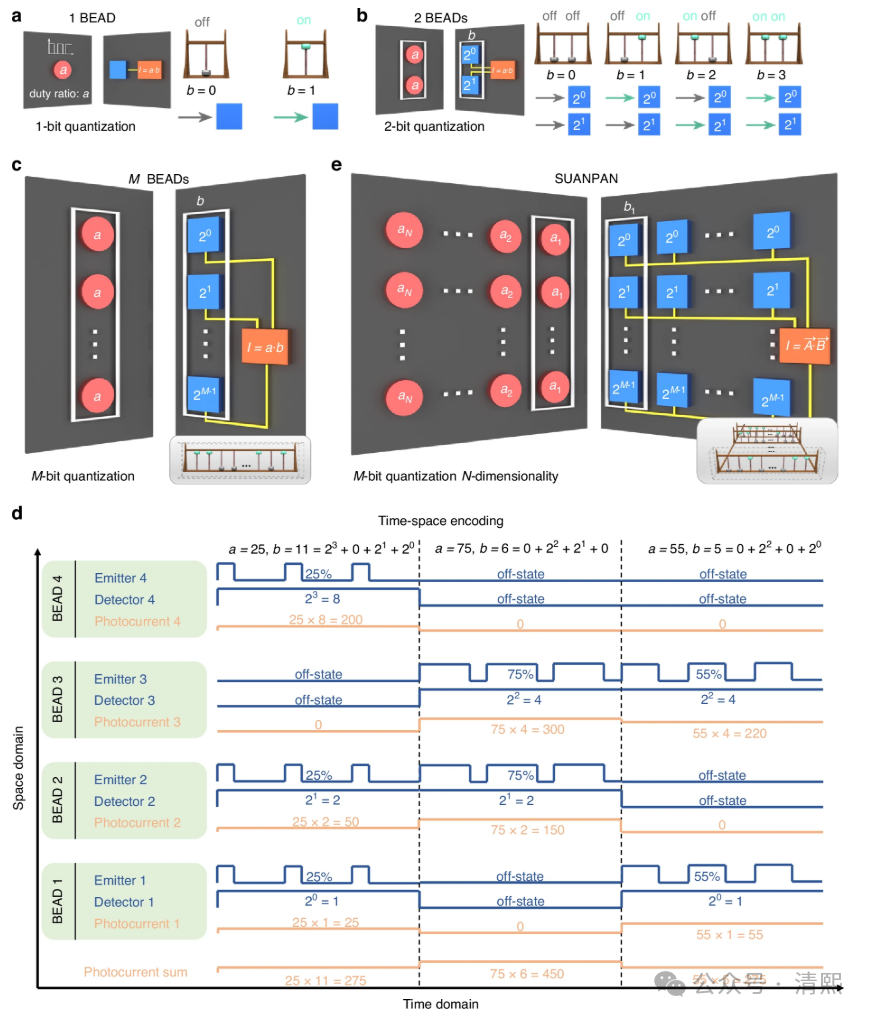
SUANPAN工作原理
这两条路线共同指向一个事实,当计算的主要代价来自决策搜索与线性代数时,继续在 GPU 上堆规模已不再是唯一的选择。
两种计算层级的分工
Transformer 在连续空间中构建一个可能性结构,回答“什么是合理的”“哪些模式在统计上成立”,擅长展开、生成和近似,却并不擅长执行最终的选择。
Ising 机擅长的是 Transformer 最不经济的那一步,在离散解空间中,通过全局耦合与竞争,完成一致性的确立。不是概率选择,而是物理裁决。
Transformer 更像是为世界生成一个丰富的候选景观,而 Ising 机则是在这一景观中,推动系统跨越相变边界,坍缩到一个稳定解。
前者依赖统计平均,后者依赖相互作用;前者擅长表征,后者擅长决定。两者并非相互替代,而是自然的分工。
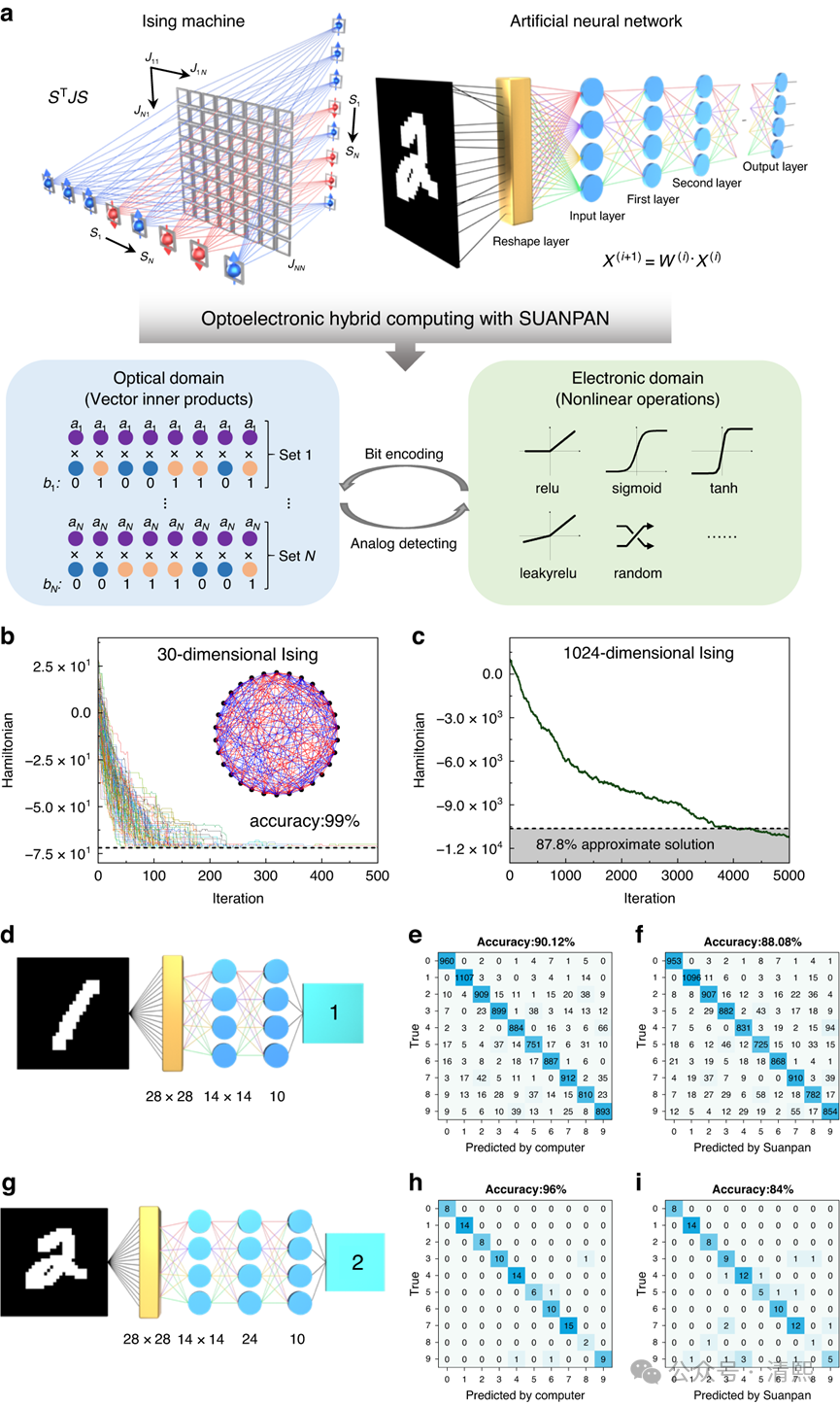
计算正在回归物理
笔者说 Transformer “尽头”,不是否定,而是承认其边界。当问题进入真实决策领域,仅靠表征学习将不可避免地遇到计算复杂度壁垒。
在这个边界上,引入自旋系统并不是激进选择,而是让目标函数、物理哈密顿量和系统动力学之间,实现高度一致。
围绕 Ising 机、光子计算和能量模型的一系列进展,并不是对现有范式的小幅加速,而是意味着一个更根本的转向:
计算正在从算法与表征,重新回归到物理与动力学。
Transformer 将我们带到了边界,而在边界之外,可能不是更多参数,而是 Ising 机。
【文献1】SUANPAN: scalable photonic linear vector machine,https://www.nature.com/articles/s41377-025-02059-7
【文献2】Programmable optoelectronic Ising machine for optimization of real-world problems,https://www.nature.com/articles/s41377-025-02100-9
文章转载自微信公众号:清熙
原文链接:https://mp.weixin.qq.com/s/ZQM4LKK5YrWEKhPNQlgs5g | 






















