聚类是无监督学习中一项基础而关键的任务,其核心目标在于发现数据中的潜在结构,并将相似对象划分至同一簇内。在图数据结构中,节点之间的关系由边显式给定,缺乏可直接度量的特征空间,使得传统聚类方法难以直接应用于图数据。谱聚类作为一类以图拉普拉斯算子的谱分解为基础的方法,能够有效地挖掘图中隐含的社团结构。本文从图论和线性代数的基本原理出发,分析谱聚类的构造逻辑,解释其物理意义与数学依据,并通过最小割问题与特征向量嵌入等视角,揭示谱聚类在图结构数据上的聚类机制。

一、聚类任务与图结构的差异性
聚类作为机器学习与数据挖掘中的核心方法之一,其主要任务是在缺乏监督信息的条件下,基于数据内部的相似性,将样本划分为若干个结构紧凑、彼此区分明显的簇。对于传统意义上的结构化数据而言,样本通常可以被表示为固定维度的特征向量,从而被嵌入至欧几里得空间之中。在此背景下,距离度量(如欧几里得距离、曼哈顿距离)成为最为自然的相似性判据,而以此为基础发展出的K均值、层次聚类、密度聚类(如DBSCAN)等算法,构成了无监督学习中一系列经典方法。
然而,当数据以图的形式呈现时,这种“特征向量—距离度量”范式便不再适用。图的基本构成单位是节点与边,节点本身可能并不具有明确的特征表示,其相互之间的关系由边的存在与否及其权重所定义。在许多实际问题中,图的结构恰恰体现了实体之间最为核心的依赖与相似关系。例如,在社交网络中,边的存在代表人与人之间的交互关系;在蛋白质相互作用网络中,边刻画蛋白之间的功能联系;在交通网络中,边则表征城市之间的可达性。在这类情形下,若仍试图将节点强行映射为某种欧氏空间特征,往往会导致信息的丢失与结构的扭曲。
因此,对于图数据而言,聚类的目标应当是识别图中的社团结构(community structure),即一组节点之间内部连接紧密,而与其他节点之间连接稀疏的子图集合。这种划分不再基于传统的距离度量,而是依赖于图的拓扑结构本身。因此,图聚类的关键问题转化为:如何根据边的分布模式与连通性特征,定义并度量“节点相似性”,并据此将图划分为若干内部密集、外部联系稀疏的子图。
在图聚类问题的建模过程中,“最小割”(minimum cut)作为一种原始的形式化目标,为聚类提供了直观的数学表征:通过删除尽可能少的边,将图划分为两个或多个子图。然而,该方法存在“割小而簇小”的偏好,容易导致划分结果中的某些簇过小,从而难以反映图中真实的社团结构。为解决此问题,一系列归一化的割函数被提出,其中最具代表性者为“归一化割”(normalized cut)与“Ratio Cut”。Normalized Cut函数方法考虑了割边的数量,也兼顾了各子图内部的规模或连通度,为谱聚类方法的提出奠定了基础。
二、图拉普拉斯算子的构造与代数性质
图拉普拉斯算子(Graph Laplacian)是谱聚类算法的核心工具,它将图的拓扑结构映射为矩阵空间中的线性变换对象,使我们得以借助线性代数中的特征值理论对图结构进行分析。Laplacian 本质上是一种差分算子,它以节点的度信息和相邻性为基础,度量图中局部连接结构的变化性,并最终作为聚类的判据。以下我们依次介绍其构造方法、矩阵形式及基本代数性质。
2.1 图的基本表示:邻接矩阵与度矩阵
设 G = (V, E) 是一个无向图,其中 V = {v₁, v₂, ..., vₙ} 是节点集合,E 是边集合。我们首先构造邻接矩阵 A ∈ ℝⁿˣⁿ,它的第 i 行第 j 列元素 Aᵢⱼ 表示节点 vᵢ 与节点 vⱼ 之间的连接关系。对于无权图,若 (vᵢ, vⱼ) ∈ E,则 Aᵢⱼ = 1,否则 Aᵢⱼ = 0。对于加权图,Aᵢⱼ 等于边的权重。由于 G 是无向图,邻接矩阵 A 是对称矩阵:Aᵢⱼ = Aⱼᵢ。与邻接矩阵相对,度矩阵 D 是一个对角矩阵,用于刻画每个节点的连接强度。具体而言,D 的对角元素 Dᵢᵢ 等于节点 vᵢ 的度数,即该节点连接的边的数量:

其余非对角元素皆为零,因而 D 是一组非负整数的对角矩阵。
2.2 无归一化拉普拉斯算子:L = D - A
最基本的图拉普拉斯算子被定义为度矩阵与邻接矩阵之差,即:

这是所谓的“无归一化拉普拉斯矩阵”(unnormalized Laplacian)。从结构上看,L 的每一行编码了某个节点与其邻居之间的连接关系与差异程度。更具体地,第 i 行第 j 列的元素定义如下:
-
若 i ≠ j 且 (vᵢ, vⱼ) ∈ E,则 Lᵢⱼ = -1;
-
若 i = j,则 Lᵢᵢ = 节点 vᵢ 的度数;
-
若 i ≠ j 且 (vᵢ, vⱼ) ∉ E,则 Lᵢⱼ = 0。
2.3 示例:一个简单的无向图
考虑以下图结构,共有 4 个节点:
-
节点 v₁ 连接 v₂ 和 v₃;
-
节点 v₂ 连接 v₁ 和 v₄;
-
节点 v₃ 连接 v₁;
-
节点 v₄ 连接 v₂。
该图的邻接矩阵 A 为:

相应的度矩阵 D 为:

据此可以计算出拉普拉斯矩阵L:

该矩阵具备以下几个代数性质(将在下一小节展开):
-
L 是实对称矩阵;
-
L 是半正定矩阵(所有特征值非负);
-
零特征值的个数等于图的连通分支数量。
2.4 Laplacian 的直观解释
从行列结构上观察,L 的每一行可视作对某一节点进行的局部差分操作,即当前节点的度减去其与邻居的连接强度之和。若将节点赋予某种标量“状态”或“电势”向量 x ∈ ℝⁿ,那么 Lx 所给出的就是该状态在图结构中的“差异传播”结果:

其中 N(i) 表示与节点 i 相邻的所有节点。这个形式表明:Lx 在第 i 个分量上是节点 i 与其邻居之间状态差异的总和。这一公式正是图拉普拉斯算子与物理中扩散过程、电流平衡之间建立联系的桥梁。
三、图拉普拉斯的物理解释与电路类比
图拉普拉斯算子虽然源自图论的代数构造,但其在许多研究中被赋予了明确的物理意义。最为常见且直观的一种解释,便是将图视为一个理想电路网络,其中节点是电势载体,边为具有导通能力的电阻通道。在这一设定下,图的拉普拉斯算子可被视为一类电流守恒定律的离散化表达形式,其作用等价于描述一个节点与其邻居之间的电势差所诱发的净电流流入量。下面我们逐步建立这一类比模型。
3.1 电势、电导与图的结构映射
设图 G = (V, E) 是一个无向、无源、线性网络,每条边都可以被看作一根电导为 1 的导线(或权重为 wᵢⱼ 的导线)。我们在每个节点 vᵢ 上施加一个电势 xᵢ ∈ ℝ,则 vᵢ 节点的电流流动受到与其相邻节点之间电势差的驱动。
根据欧姆定律与基尔霍夫电流定律,一个节点 vᵢ 的净电流输入量应为其所有邻接边上电势差所对应的电流之和。设 x 为电势向量 x = [x₁, x₂, ..., xₙ]^T,则节点 vᵢ 的电流流入量为:

与2.4的公式相对比,我们可以明显发现,这正是拉普拉斯作用于向量 x 所得到的结果。因此,整个网络的电流分布由向量 Lx 表示,它刻画了每个节点相对于邻域的“电势失衡”状态。
3.2 对称性与物理保守性
正如上面所说,Laplacian 矩阵具有以下几个具有数学意义,也与电路系统中的物理守恒特性密切相关的重要性质:
-
L 是实对称矩阵:这意味着其特征值为实数,且存在一组正交的特征向量。这一性质使得可以通过谱分解方法构造潜在的低维嵌入表示。
-
L 是半正定矩阵:对任意向量 x,有 xᵀ L x ≥ 0,并且等于零当且仅当 x 为常数向量。这反映了物理意义上能量最小的状态即为系统处于“电势均衡”——即电流静止——的状态。
-
L 的零特征值对应电势恒定分布:当 x = [1, 1, ..., 1]^T(所有节点电势相等)时,Lx = 0,表示系统中无电流流动。这个结论完全符合静态电场理论中的基本事实。
进一步地,L 的特征值 λ 和特征向量 φ 共同满足:
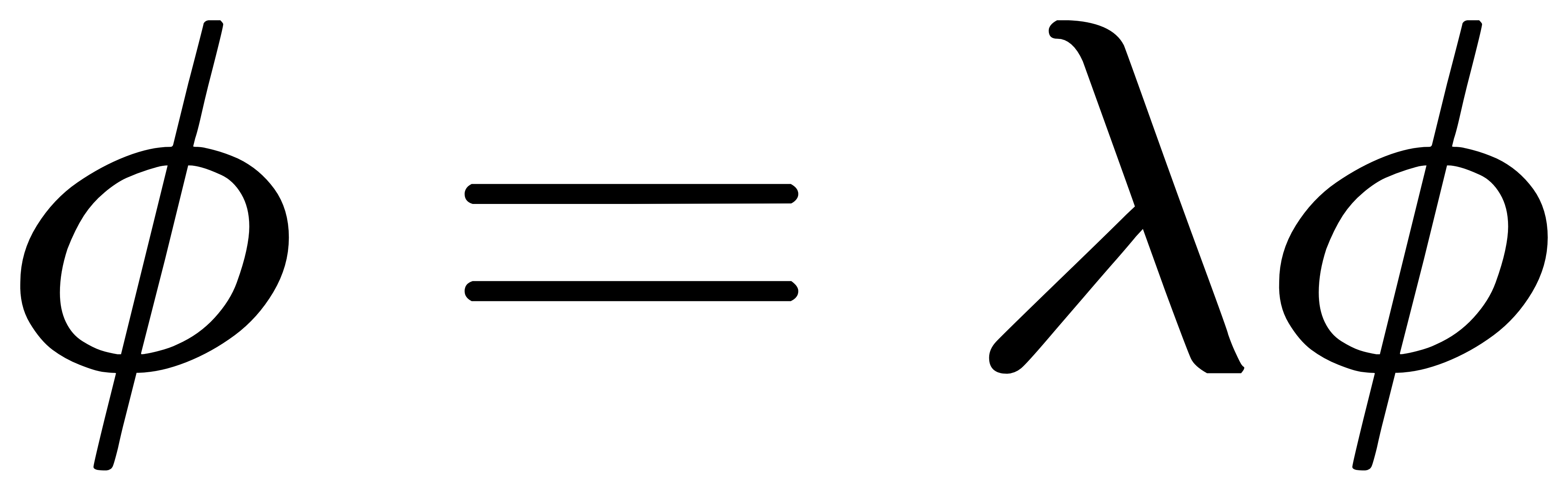
其中 λ 表示对应的能量态,φ 则为某一电势分布模式。拉普拉斯谱(即所有特征值的集合)可以理解为系统所有可能“能量状态”的集合,而每个特征向量则是一种潜在的电势分布模式。
3.3 电势相近性与“弱流动”的聚类启示
那么,如何从上述电路类比中推导出聚类的动因?我们回到物理过程的直觉判断:若图中某一组节点之间连接密集、互为邻居,其内部的“电势差”应尽可能小,以减少电流在该区域内的流动。这意味着这部分子图的节点电势趋于一致,其净电流趋于最小。这种内部流动低、外部联系弱的结构,正是我们试图通过聚类所捕捉的“社团”。
换言之,在整个图中,若存在若干个节点集合(簇),其内部具有近似一致的电势分布,而不同簇之间电势差异明显,则这些集合可被视为结构上稳定的划分单位。这种“低能量态”的划分,正是谱聚类所追求的目标。
这也解释了为何拉普拉斯的第二小特征值及其对应的特征向量(即所谓的Fiedler 向量)在图划分中具有核心地位。我们将在后续章节中进一步详细讨论特征值与聚类边界之间的联系。
3.4 能量函数与最小化视角
为了进一步刻画“电势趋同”的代数表达,我们引入以下图能量函数:

该函数可理解为图中所有边的“电势差平方”的加权和,它度量了整个图在给定电势分布下的总能量。最小化 E(x) 即意味着找到一组尽可能均衡的电势配置,使得相邻节点之间的差异最小。
但正如前文所述,最小化 E(x) 的极小值为 0,其解为常数向量(即所有节点电势相等),这在聚类中是无意义的。因此我们需要引入附加约束,例如要求向量 x 与常数向量正交(∑xᵢ = 0,或 ∥x∥ = 1),以避免退化解。这便引出了基于特征向量的最优化问题与谱分解方法。
四、图拉普拉斯的特征值分解与谱聚类的原理
图拉普拉斯算子将图结构编码为矩阵空间中的线性变换,进而可通过特征值分解(spectral decomposition)的方法提取其内部的谱特征。谱聚类正是利用拉普拉斯矩阵的谱信息来重构节点之间的低维表示,并据此完成聚类划分。在本节中,我们将详细解释谱聚类的数理逻辑,阐明其背后的优化问题与谱代数基础。
4.1 图切割与优化目标函数
图聚类最直接的数学形式,是最小化跨簇连接边的权重总和。这种目标被形式化为最小割问题(minimum cut),其定义如下:
设图 G = (V, E),将节点集合 V 划分为两个互不重叠的子集 A 和 B,最小割的目标是使以下函数最小:

其中 Aij是邻接矩阵的元素,表示边 (i, j) 的权重。
但最小割方法有一个固有缺陷:它倾向于将图划分为极小的不均衡子图,从而形成非结构性的割。为克服这一问题,后续研究引入了归一化割(normalized cut, Ncut)和RatioCut等更合理的目标函数,例如 Ncut 定义为:

其中 Vol(A) = ∑A di是 A 中节点的度总和。然而,这类组合优化问题通常是 NP-hard 的,难以直接求解。因此谱聚类采取松弛优化策略,通过构造拉普拉斯特征向量空间的连续逼近解,来代替原本的离散划分问题。
4.2 特征向量嵌入与第二小特征值
谱聚类的核心思想是:图中社团结构可以通过图拉普拉斯矩阵的前几个特征向量所张成的低维子空间来刻画。特别地,第二小特征值(也称为代数连通度,algebraic connectivity)所对应的特征向量,称为Fiedler 向量,在二分类聚类中具有决定性作用。
设 L 为无归一化拉普拉斯矩阵,考虑其特征值分解:

其中 U 为正交矩阵,其列向量为特征向量,Λ 为对角特征值矩阵,满足:
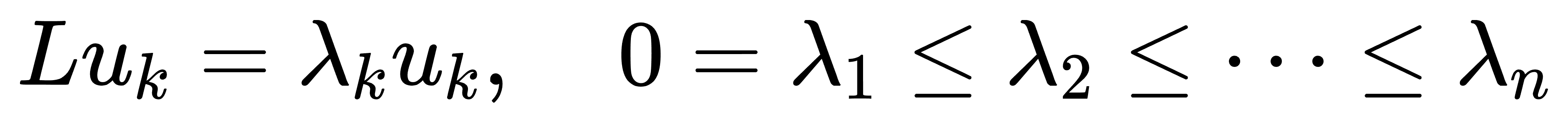
-
特征值 λ₁ = 0,对应的特征向量为常数向量 u₁ = [1, 1, ..., 1]^T;
-
第二小特征值 λ₂ 通常大于 0,其对应的特征向量 u₂ 在结构上具有划分指向性;
-
特征向量 u₂ 的符号可用于将图划分为两个部分:正分量对应一类,负分量对应另一类。
换言之,u₂ 实际上提供了一个将高维图结构映射到一维实数轴的方式,而该一维轴上的投影位置反映了节点间的结构相似性。通过对 u₂ 进行符号分割或聚类处理(例如用 K-means),即可实现结构感知的图聚类。
4.3 低维谱嵌入与多簇划分
对于更一般的 k 类划分问题(k > 2),谱聚类不再只使用第二小特征向量,而是取拉普拉斯矩阵的前 k 个特征向量 u₁, ..., u_k,构造节点的低维表示矩阵 X ∈ ℝⁿˣᵏ,其中 Xᵢ 为节点 i 在特征空间中的嵌入向量。
此时,每个节点被映射为 ℝᵏ 空间中的一个点,彼此间的位置关系反映了原图中的拓扑相似性。最终,可以在该嵌入空间中使用 K-means 等传统聚类方法进行划分,从而完成整个谱聚类流程:
-
构造图的邻接矩阵 A 与拉普拉斯矩阵 L;
-
计算 L 的前 k 个特征向量,构成嵌入矩阵 X;
-
对 X 的每一行作为特征向量,进行 K-means 聚类;
-
将聚类结果映射回原图,得到节点的聚类标签。
这种方法本质上将图聚类问题转化为对节点在“最小能量扰动空间”中的位置进行几何划分的问题,极大地降低了结构复杂性。
4.4 示例说明:Fiedler 向量与划分边界
我们再次回到前述 4 节点图的例子,其拉普拉斯矩阵 L 为:

计算其特征值与特征向量,可以得到(略去数值计算过程)第二小特征值 λ₂ ≈ 0.585,其对应的特征向量 u₂ ≈ [0.5, 0.5, -0.5, -0.5]。我们可以观察到 u₂ 的符号直接将图分为两个部分:节点 1 和 2 在正轴,节点 3 和 4 在负轴。这正是图中天然的两类结构。若我们采用 K-means 方法将 u₂ 分为两个簇,便可得到几乎完美的图聚类结果。
结语:谱方法对图结构理解的启示
通过图拉普拉斯算子的引入与特征谱的解析,谱聚类方法展现出一种深具结构感知能力的聚类机制。它不仅规避了传统最小割策略中的不均衡性问题,更从“最小扰动”、“电势趋同”与“能量优化”的角度重新定义了节点之间的相似性。在图这一非欧几里得结构中,谱聚类之所以有效,归根结底是因为它利用了图的代数结构对拓扑连接性进行编码,并通过特征向量构造出一种与结构密切相关的几何嵌入。
从数学角度看,图拉普拉斯的特征值谱蕴含着丰富的结构信息:零特征值的数量揭示图的连通性,第二小特征值衡量图的整体可分性,而其对应的特征向量则为聚类提供了明确的方向与空间。谱方法不仅可以作为聚类手段,还可用于图分割、节点排序、半监督学习等多个方向,已成为图论、机器学习与网络科学中的基础工具之一。
在实践中,谱聚类尤其适用于中小规模图结构的结构识别问题,或作为复杂模型(如图神经网络)预训练与结构感知初始化的一部分。尽管其在计算效率上存在特征值分解带来的限制,但近年来关于近似谱方法、稀疏图加速等技术的发展,正逐步扩展其在大规模图数据中的可行性。而从更为抽象的层面看,谱聚类提供了一种重要的转变:我们不再试图在显式特征空间中刻画数据间的距离,而是通过谱结构理解“关系”本身的几何本质。因此,从结构出发的思维方式,将继续在图学习、网络科学、量子信息、复杂系统等众多领域中,发挥深远的影响。
| 


