本帖最后由 graphite 于 2025-7-29 06:50 编辑
本文提出 DVAE# 框架,通过两种连续松弛方法将玻尔兹曼机转化为连续分布,允许用重要性加权界训练离散变分自编码器,并泛化重叠变换,引入幂函数等新变换。实验显示,在 MNIST 和 OMNIGLOT 数据集上,DVAE#(幂函数变换)性能优于 DVAE 和 DVAE++,如 MNIST 的 2∼结构中,其负对数似然为 82.85±0.03,低于 DVAE 的 84.19±0.21 和 DVAE++ 的 83.58±0.15。K 值越大,优势越明显,验证了方法有效性。
你可能听说过生成式 AI 的神奇 —— 让机器学会 "创造",比如生成逼真的图片、音乐甚至分子结构。其中,变分自编码器(VAE)是一种强大的生成模型,它通过 "编码 - 解码" 的过程,用潜变量来捕捉数据的本质规律。
过去,VAE 的成功大多依赖连续潜变量,因为它们可以用 "重参数化技巧" 高效训练。但在很多场景中,离散潜变量更实用:它们计算效率更高,解释性更强,在聚类、半监督学习等任务中不可或缺。
早在深度学习兴起前,玻尔兹曼机就是处理离散潜变量的利器。这种模型能表示任意二进制变量的分布,在无监督学习、推荐系统等领域大显身手。近年来,研究者尝试将玻尔兹曼机作为先验,融入 VAE 框架,提出了离散变分自编码器(DVAE)及其改进版DVAE++。
但问题来了:这些早期模型只能用较松的 "变分下界" 训练,而更紧的 "重要性加权下界"(IW bound)—— 已被证明能显著提升连续潜变量 VAE 的性能 —— 却无法应用于离散潜变量模型。这就像给赛车装了限速器,明明有更强的动力却用不上。
正是这个瓶颈,催生了今天要聊的研究 ——DVAE#。它的核心目标是:让离散潜变量模型也能用上 IW bound,释放玻尔兹曼机先验的真正潜力。
这篇在 2018 年发表于 NeurIPS 的论文,主要有以下两个里程碑式的贡献:
玻尔兹曼机的连续松弛方法:提出两种将离散玻尔兹曼机转化为连续分布的方法,使得 IW bound 可以用于训练离散 VAE。这就像把 "离散的台阶" 变成 "连续的斜坡",让原本只能在台阶上缓慢移动的训练过程,能在斜坡上顺畅加速。
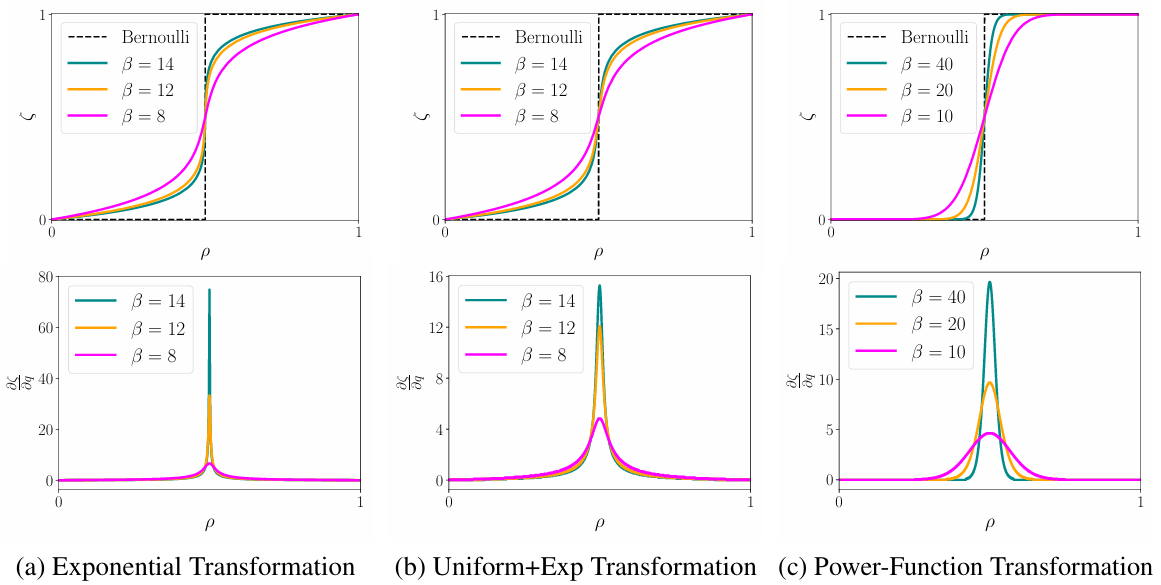
图1 不同重叠变换的逆 CDF 及梯度可视化
通用化的重叠变换:扩展了 DVAE++ 中用于连接离散变量和连续变量的 "重叠变换",使其适用于任何具有可计算概率密度函数(PDF)和累积分布函数(CDF)的分布。基于此,提出了幂函数、均匀 + 指数等新的平滑变换,其中幂函数变换在高逆温度下表现最佳 —— 既能精准逼近离散变量,又能保持较低的梯度方差)。
要理解 DVAE# 的创新,我们需要从 "离散潜变量的训练难题" 说起。
离散潜变量的训练困境
VAE 训练的核心是最大化 "边际对数似然的变分下界",其中涉及对潜变量的期望计算。对于连续潜变量,我们可以用 "重参数化技巧" 将期望转化为可微分的采样过程;但对于离散潜变量,由于其累积分布函数(CDF)不可微,这个技巧失效了。
早期的 DVAE 通过给每个离散变量 z 配对一个连续辅助变量 ζ,绕过了这个问题,但代价是无法使用更紧的 IW bound。IW bound 的优势在于:它通过多个样本的加权平均逼近真实分布,样本数 K 越大,下界越紧,模型性能越好。DVAE# 的目标就是让离散模型也能享受这个优势。
玻尔兹曼机的连续松弛
DVAE# 提出两种将离散玻尔兹曼机先验 p (z) 转化为连续分布 p (ζ) 的方法,这样就能用连续潜变量的训练技巧了。
方法一:重叠松弛(Overlapping Relaxations)
核心思想:通过 "边际化" 将离散分布扩展为连续分布。具体来说,定义连续潜变量 ζ 的分布为:
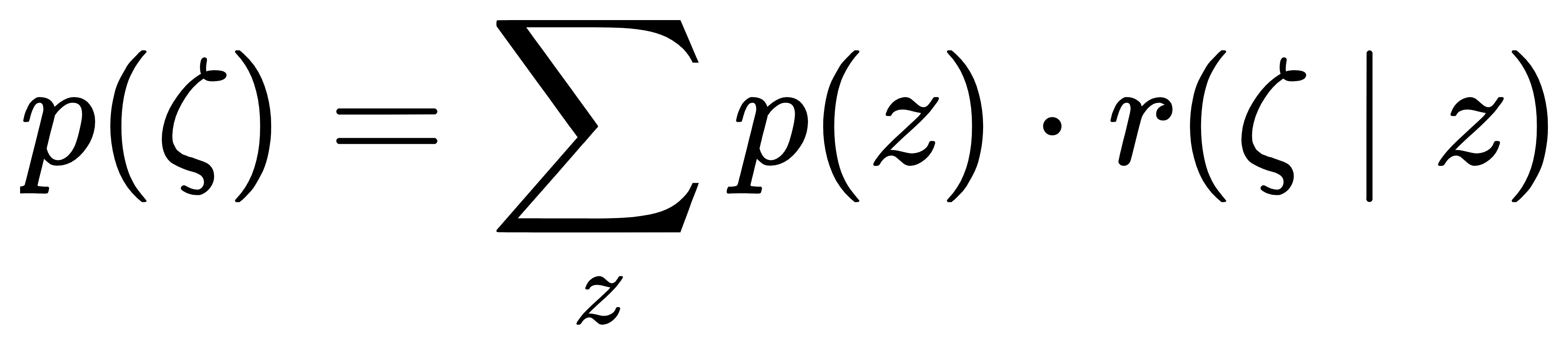
其中,z 是二进制潜变量,p (z) 是玻尔兹曼机先验(p(z)=e−Eθ(z) /Zθ ,Eθ(z)是能量函数),r(ζ∣z) 是 "重叠平滑变换"—— 它为每个 z 分配一个连续分布,且这些分布在 ζ 的空间中相互重叠。
这里的关键是逆温度参数 β:β 越大,r(ζ∣z) 越 "尖锐",越接近离散的 δ 函数(即 ζ≈z);β 较小时,分布更平缓,连续特性更明显。这就实现了 "从连续到离散" 的平滑过渡。
计算 log p(ζ) 时,由于直接对所有 z 求和(2D项,D 是潜变量维度)不可行,论文用平均场近似简化:假设潜变量各维度独立,用迭代方法最小化 KL 散度,快速逼近真实分布。梯度计算则通过下式近似:
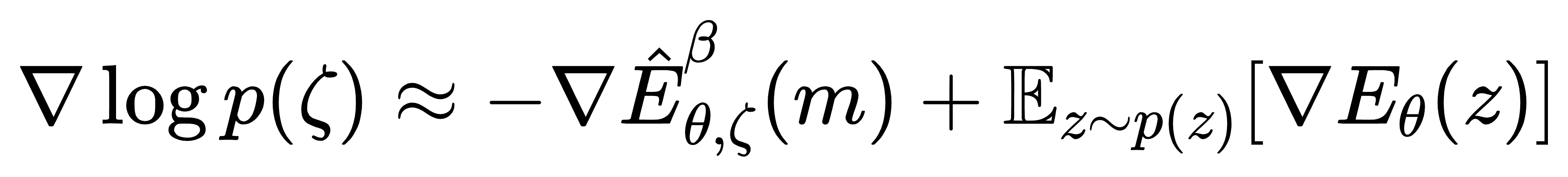
其中 m 是平均场解,E^θ,ζβ 是增强的能量函数。
方法二:高斯积分技巧(Gaussian Integral Trick)
另一种思路是利用物理中的 "Hubbard-Stratonovich 变换",将玻尔兹曼机中复杂的 pairwise 相互作用( zTWz )通过高斯积分移除,直接得到连续分布。
最终得到的连续先验 p (ζ) 是高斯混合模型:每个混合成分对应一个二进制 z,中心在超立方体的顶点(z 的取值),协方差由 (W+βI) −1 决定。公式如下:
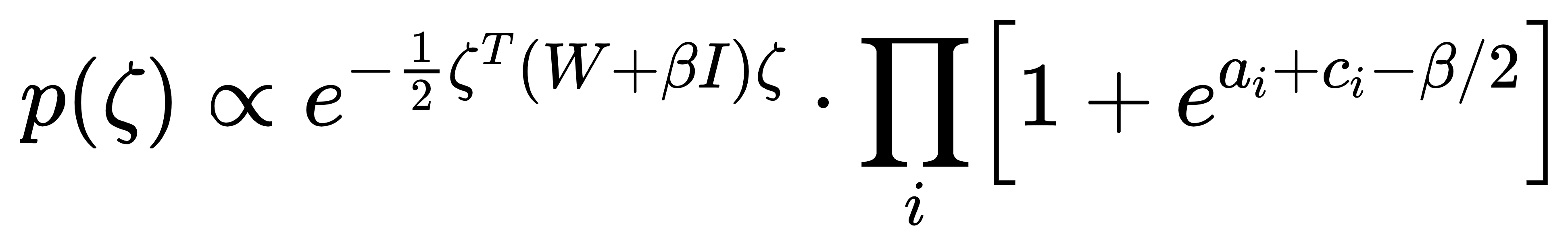
当 β→∞时,每个高斯成分退化为 δ 函数,p (ζ) 逼近原始离散分布。
通用化的重叠变换
早期的 DVAE++ 只能用指数分布等少数重叠变换,而 DVAE# 将其推广到任意具有可计算 PDF 和 CDF 的分布。
核心是用隐函数定理计算梯度:对于混合分布q(ζ∣x)=(1−q)r(ζ∣z=0)+qr(ζ∣z=1)(q 是 z=1 的概率),其 CDF 满足(1−q)R(ζ∣0)+qR(ζ∣1)=ρ(ρ 是均匀采样的噪声)。对 q 求导得:
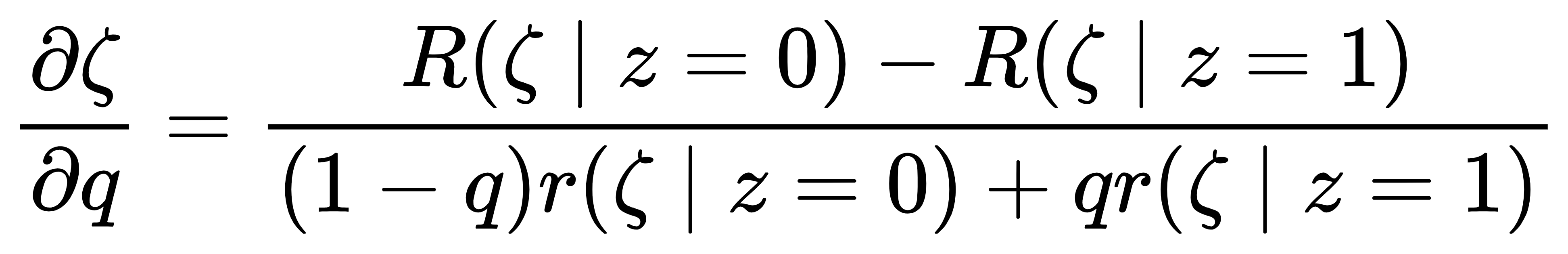
这让非解析逆 CDF 的分布也能计算梯度,由此诞生了两种新变换:
均匀 + 指数变换:在指数分布中混入少量均匀分布,避免 β 过大时梯度爆炸。
幂函数变换:基于 Beta 分布,形式为:
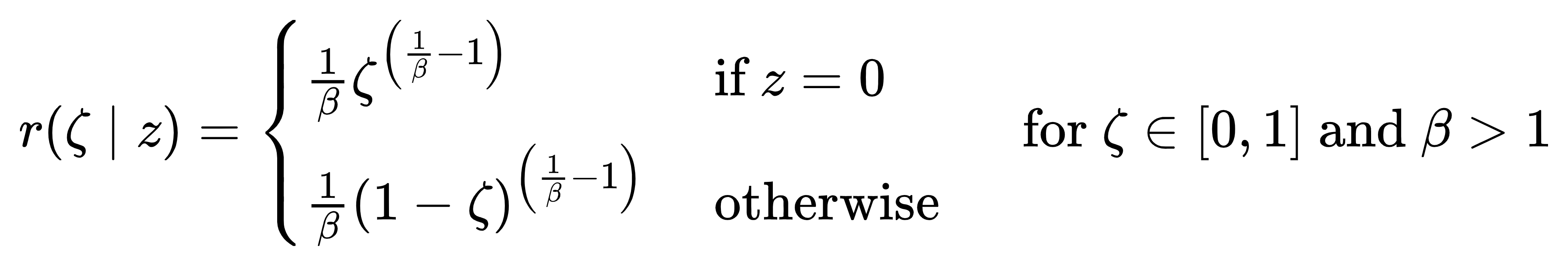
它在 β 很大时仍能保持较低的梯度方差,这是其性能优异的关键。
运用 IW bound 的训练框架
有了连续先验 p (ζ),DVAE# 就能用 IW bound 训练了。K 个样本的 IW bound 定义为:
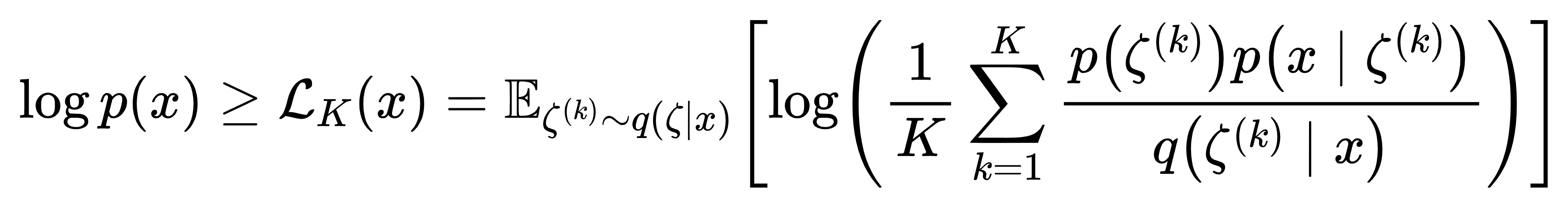
其中 q (ζ|x) 是编码器的近似后验。K 越大,下界越紧,模型对数据分布的捕捉越精准。
04 实验验证
论文在 MNIST 和 OMNIGLOT 两个经典数据集上做了实验,用负对数似然(NLL) 衡量模型性能,NLL 越低,生成能力越强。
DVAE# 全面超越前辈
对比 DVAE、DVAE++ 和 DVAE# 的关键数据,部分结果如下:
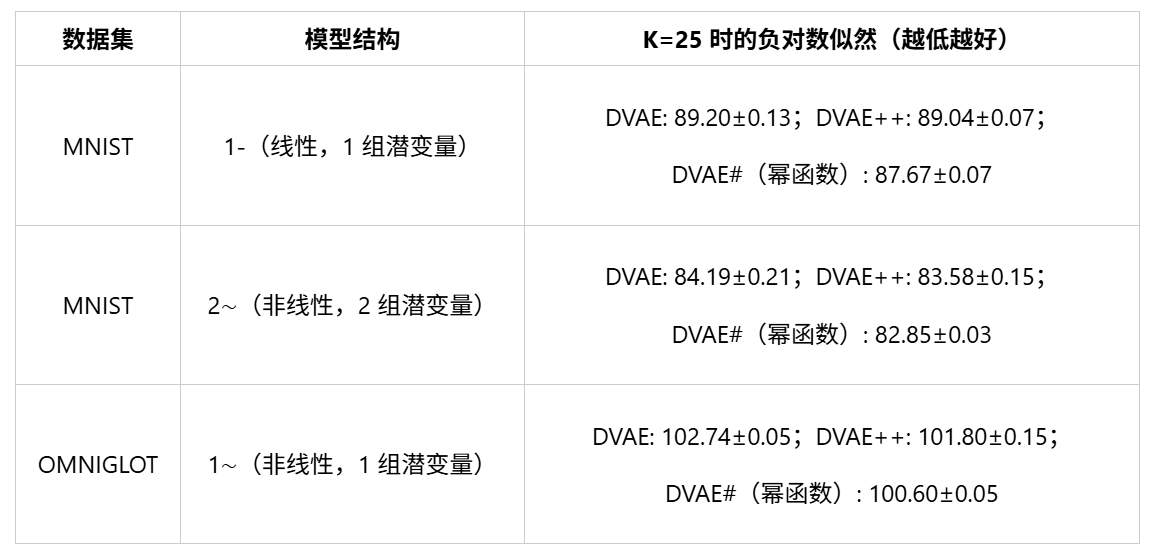
从数据可见,DVAE#,尤其是幂函数变换,在所有设置下都优于 DVAE 和 DVAE++,且 K 越大,优势越明显。例如在 MNIST 的 2∼结构中,DVAE# 的 NLL 比 DVAE 低了 1.34,意味着生成的数字更接近真实数据分布。
为什么幂函数变换更好?
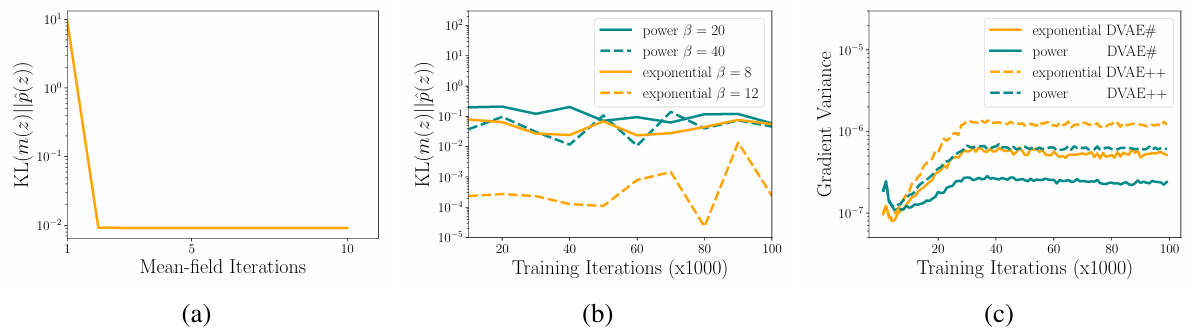
图2 均值场近似收敛及不同平滑变换的 KL 散度和梯度方差
如图 2 所示,实验发现,幂函数变换的梯度方差显著低于指数变换。例如,当 β=30 时,幂函数变换的梯度方差约为指数变换的 1/5。更低的方差意味着训练更稳定,能更快收敛到更优解。
05 结论
DVAE# 通过两种连续松弛方法,首次让离散潜变量模型用上了 IW bound,同时推广了重叠变换,提出了性能更优的幂函数平滑策略。实验证明,它在生成任务上全面超越 DVAE 和 DVAE++,为等需要离散潜变量的场景提供了更强的工具。
这项研究的意义不仅在于性能提升,更在于它打破了 "离散潜变量无法高效使用紧下界" 的限制,为离散生成模型的发展开辟了新道路。未来,我们或许能看到更多结合离散潜变量优势和连续训练技巧的创新模型。
论文链接:DVAE#: Discrete Variational Autoencoders with Relaxed Boltzmann Priors
GitHub:https://github.com/QuadrantAI/dvae | 

