本帖最后由 离子 于 2025-6-25 18:32 编辑
本文提出了一种利用量子玻尔兹曼机(QBM)生成高维数据分布的方法,解决了经典玻尔兹曼机在处理复杂高维分布时的局限性。QBM通过量子比特的非对易相互作用,能够有效地表示更复杂的分布。实验结果显示,QBM在模拟粒子喷流事件和高维数据生成任务中,优于经典玻尔兹曼机,特别是在计算效率和精度方面。研究还展示了QBM与经典方法在训练过程中的对比,验证了TPQ方法的高效性。QBM为未来量子计算应用提供了强有力的工具,尤其在粒子物理和复杂数据建模领域具有巨大潜力。

近年来,量子计算在多个领域取得了显著进展,特别是在生成模型方面,这些模型用于学习表示复杂的概率分布。由Cenk Tüysüz、Maria Demidik、Luuk Coopman等学者共同撰写的论文《Learning to generate high-dimensional distributions with low-dimensional quantum Boltzmann machines》(学习使用低维量子玻尔兹曼机生成高维分布)提出了一种创新方法,利用量子玻尔兹曼机来解决传统玻尔兹曼机难以处理的高维数据生成问题。
生成模型的挑战:高维数据的表示
生成模型的目标是学习给定数据集的联合概率分布,并生成符合该分布的新样本。生成模型在各个领域中都发挥着重要作用,从药物发现到天气预报,通过学习联合概率分布,这些模型能够生成新的数据样本。经典的玻尔兹曼机是一种重要的生成模型,它通过一个二元随机变量的网络来表达目标分布。然而,传统的玻尔兹曼机在处理高维、复杂的概率分布时,往往面临表示能力不足的挑战。
在本研究中,作者提出了量子玻尔兹曼机作为一种解决方案,利用量子力学中的非对易性来增加模型的表达能力,从而能够有效地学习高维数据分布。
完全可见量子玻尔兹曼机
本研究的主要突破在于使用完全可见量子玻尔兹曼机。传统的玻尔兹曼机模型依赖于可见单元和隐藏单元的组合,但完全可见模型有时在表达复杂分布时缺乏足够的能力。然而,这项研究显示,低维的完全可见量子玻尔兹曼机能够表示更高维的分布,这使其在处理传统玻尔兹曼机无法处理的复杂问题时具有更强的能力。

图1 主要结果概览
图 1 展示了量子玻尔兹曼机与经典玻尔兹曼机在生成概率分布时的能力对比。在此图中,完全可见玻尔兹曼机(fully-visible BM)可以生成与其连接性相匹配的分布,适用于通过邻近统计生成的分布。另一方面,完全可见量子玻尔兹曼机(fully-visible QBM)可以生成由更高维模型生成的分布。与此相比,经典的限制玻尔兹曼机也能够学习这两种分布,但需要额外的隐藏单元才能实现。
量子玻尔兹曼机能够表示那些涉及多个二元单元相互作用的分布,而经典的完全可见玻尔兹曼机则难以处理此类问题。量子玻尔兹曼机与经典玻尔兹曼机的一个关键区别在于其能量模型的表示方式。在经典玻尔兹曼机中,系统的能量由哈密顿量表示,通常仅包含对角项。然而,在量子玻尔兹曼机中,能量模型通过量子比特的Pauli矩阵来表示,因此可以更灵活地处理高维关联。
在量子玻尔兹曼机的设计中,哈密顿量的选择对模型的表现有重要影响。表1展示了不同类型的二局部哈密顿量定义,它们对应于不同的物理模型和计算任务。每个标签代表一个哈密顿量类型,其中P1和P2分别表示一体和二体相互作用的保利矩阵。通过选择不同的哈密顿量配置,可以模拟具有不同物理特性的量子系统,如经典的伊辛模型、具有随机相互作用的自旋玻璃模型以及其他通用的模型。
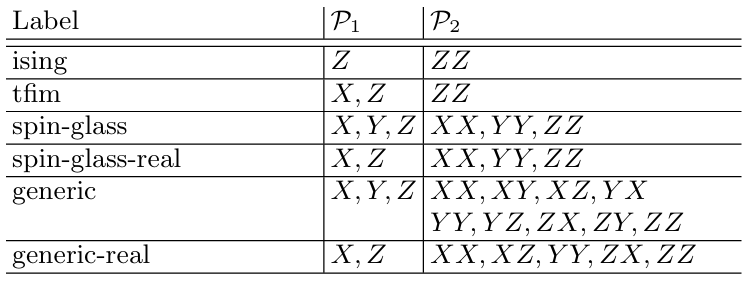
表1 二局部哈密顿量定义表
数学模型与哈密顿量
量子玻尔兹曼机的核心是其能量函数,即哈密顿量。经典玻尔兹曼机的哈密顿量形式通常如下:
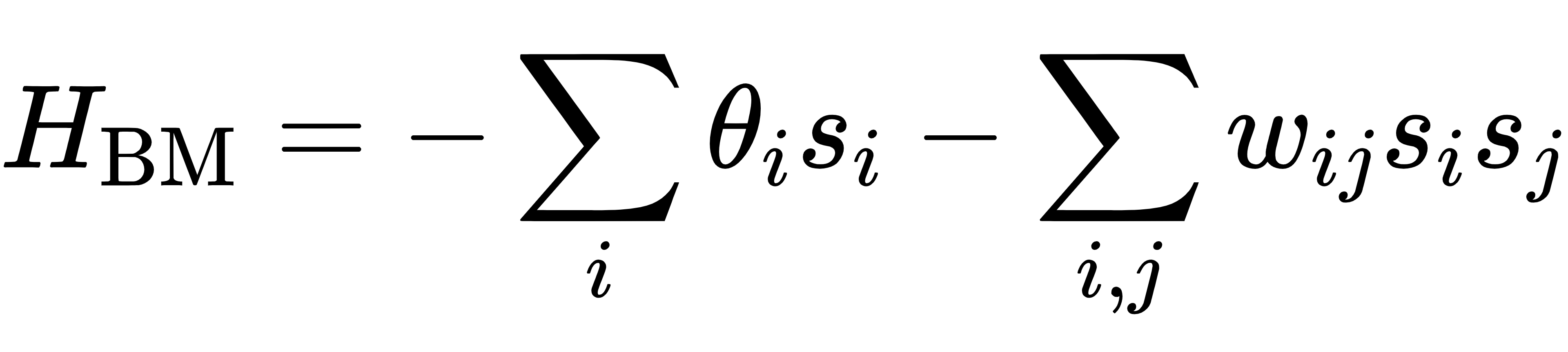
其中,𝑠𝑖 是二元变量( ±1 ),𝜃𝑖 是系统的偏置项,𝑤𝑖𝑗 是权重,节点间连接的权重。第一个求和项表示节点的单独偏置,第二个求和项表示节点之间的相互作用。这一公式说明了经典玻尔兹曼机是如何通过计算节点之间的相互作用能量来生成数据分布的。
尽管经典玻尔兹曼机可以模拟一些复杂的概率分布,但它的表达能力是有限的,特别是在处理具有高阶关联的复杂分布时,它的表现通常会受到限制。
量子玻尔兹曼机通过量子力学的哈密顿量来表示能量。在量子玻尔兹曼机中,哈密顿量不仅包括经典玻尔兹曼机中的节点偏置项和相互作用项,还涉及到量子比特之间的量子操作。具体来说,量子玻尔兹曼机的哈密顿量可以表示为:
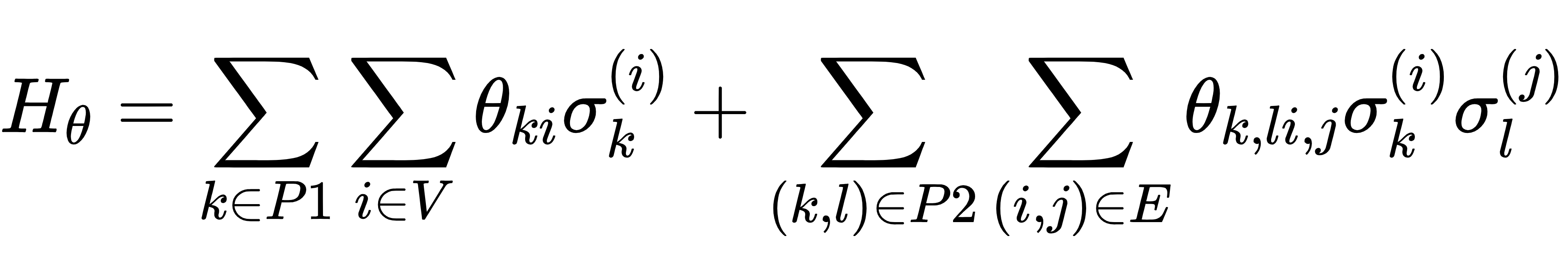
其中,P1 是单体Pauli矩阵集合,用于表示量子比特的局部操作;P2 是二体Pauli矩阵集合,用于表示量子比特之间的相互作用;𝜎𝑘(𝑖) 是保利矩阵操作( 𝜎𝑥 , 𝜎𝑦 , 𝜎𝑧 )作用于第 𝑖 个量子比特;𝜃𝑘𝑖 和 𝜃𝑘,𝑙𝑖,𝑗 是需要学习的参数,分别表示单体和二体相互作用的权重。
该哈密顿量的形式揭示了量子玻尔兹曼机如何利用量子力学的保利矩阵来建模数据的复杂分布。经典玻尔兹曼机的哈密顿量通常仅考虑二体相互作用,而量子玻尔兹曼机引入了量子比特之间的非对易Pauli矩阵,使得模型能够表示更复杂的分布,包括高维关联和量子纠缠。
量子玻尔兹曼机的训练
损失函数
量子玻尔兹曼机的训练目标是使生成的分布尽可能接近目标分布。为此,作者使用了量子相对熵作为损失函数,该损失函数可以衡量目标分布与模型分布之间的差异。量子相对熵定义为:
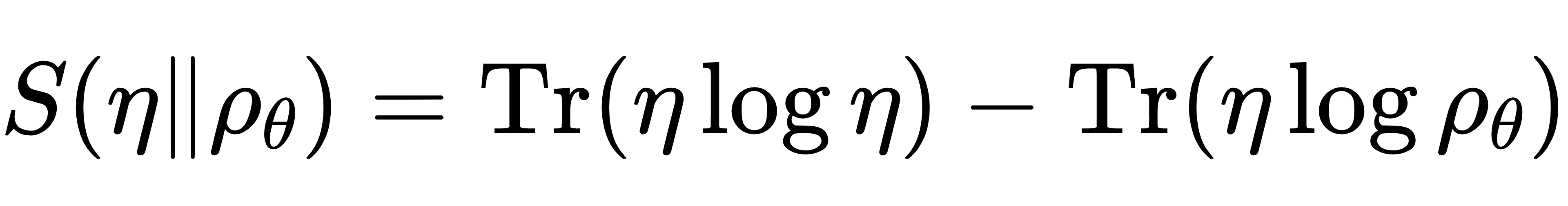
其中,𝜂 是目标分布,𝜌𝜃 是量子玻尔兹曼机生成的分布。训练过程中,我们通过最小化这个量子相对熵来优化模型参数,使得生成的分布逐渐接近目标分布。
梯度计算与优化
在训练过程中,量子相对熵的梯度计算公式为:
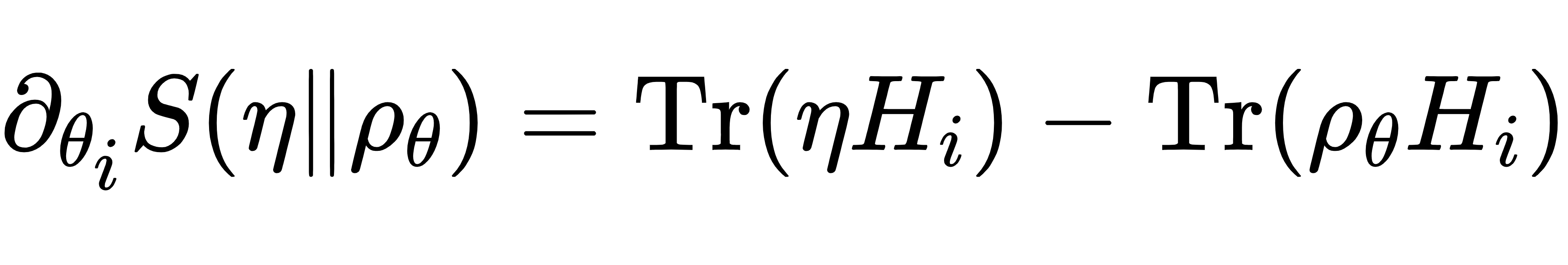
其中,𝜂 和 𝜌𝜃 分别是目标分布和量子玻尔兹曼机模型的分布 𝐻𝑖 是哈密顿量的每一项。通过计算期望值的差异,我们可以逐步优化量子玻尔兹曼机的参数。
使用热纯量子状态(TPQ)进行训练
在训练过程中,QBM通常需要计算哈密顿量的期望值。为避免计算的高昂成本,本文采用了热纯量子状态(TPQ)的方法。TPQ状态是一种通过虚时间演化生成的量子纯态,用于近似计算吉布斯状态的期望值,进而减少量子计算的资源消耗。TPQ状态的生成公式为:
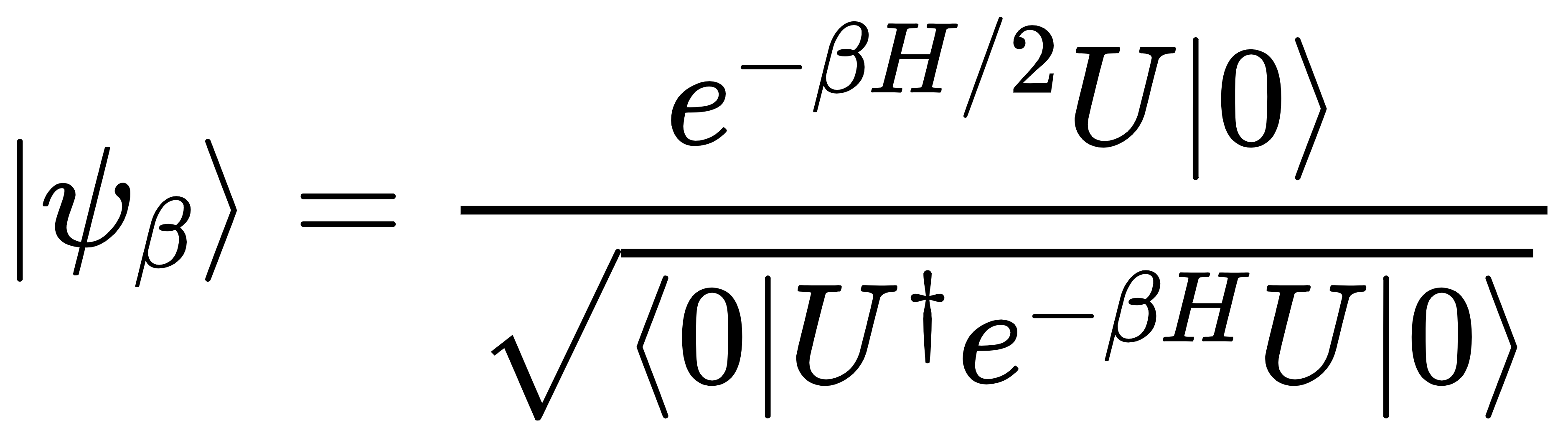
其中,U 是从量子比特克利福德群(Cl(2n))中随机选择的单位矩阵,β 是逆温度。分子部分表示在虚时间演化下作用于初始基态 ∣0⟩ 后得到的量子态;分母部分是确保状态规范化的因素,该部分是通过测量状态 ∣0⟩ 在演化过程中的期望值来实现的。TPQ状态能够近似估算期望值,而无需完全对角化哈密顿量,这大大降低了计算成本。
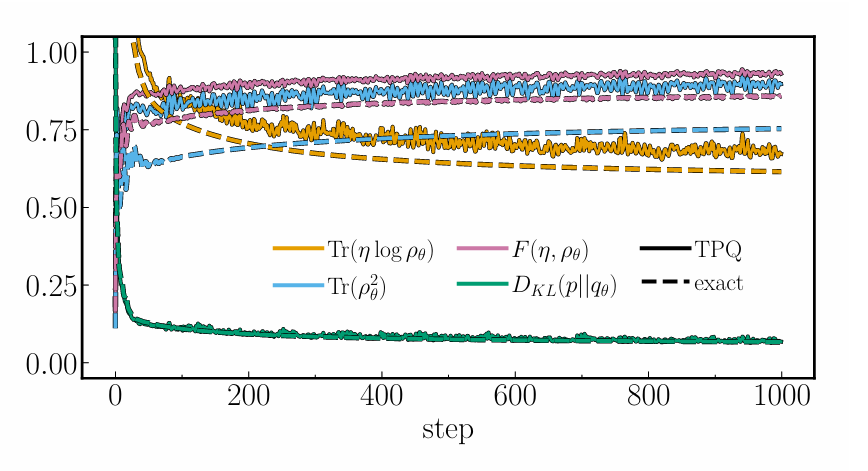
图2 QBM训练曲线比较:精确方法与TPQ方法
如图2,作者比较了使用精确方法与热纯量子状态方法训练量子玻尔兹曼机的效果。虚线使用精确的分布进行训练,而实线使用TPQ状态训练模型。从图中可以看到,使用TPQ方法训练QBM时,训练过程的收敛速度相较于精确方法更为快速。在前200步的训练中,TPQ方法迅速减小了损失函数的值,表明该方法能有效逼近目标分布。而精确方法的训练过程则较为缓慢,且在一定的训练步骤后,损失值趋于平稳。
量子玻尔兹曼机的应用与实证
作者通过一系列实验验证了量子玻尔兹曼机在多个高维分布学习任务中的有效性,尤其是在粒子喷流事件生成的实际问题中。实验中,量子玻尔兹曼机被用来生成粒子喷流事件的概率分布。粒子喷流是高能物理实验中常见的现象,尤其是在粒子碰撞中产生的多个粒子的集合。传统的模拟方法,如蒙特卡罗方法,计算量大且处理起来复杂。相比之下,量子玻尔兹曼机能够有效建模这些复杂的高维数据分布,并生成比传统方法更为高效且准确的模拟结果。
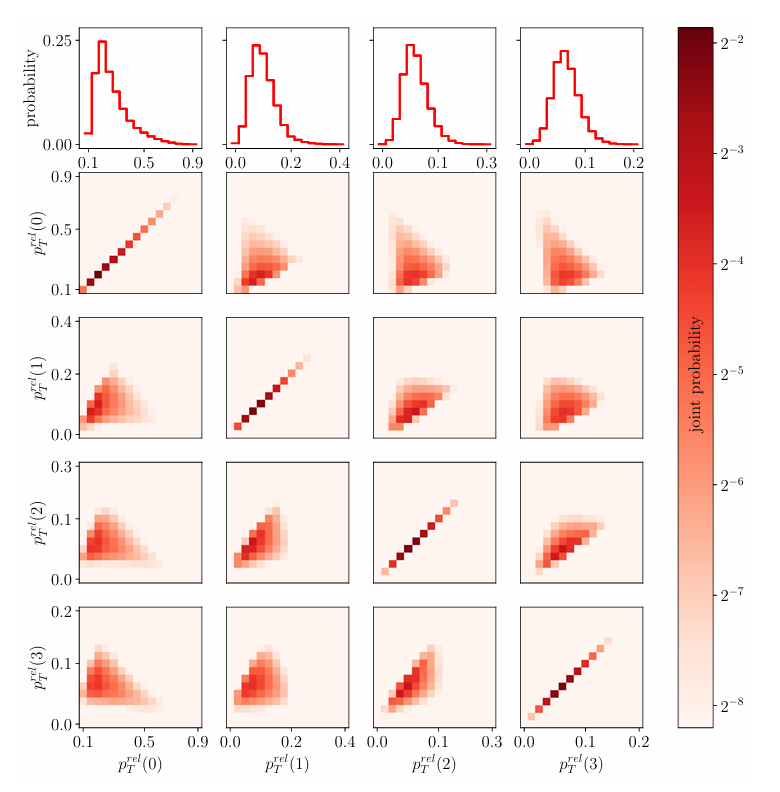
图3 四粒子联合概率分布的一维和二维投影
图3展示了四粒子联合概率分布的不同维度投影。上方一行是每个粒子的边缘分布。除了对角线部分的其他行展示了粒子对之间的联合概率分布。每个图中的颜色条表示联合概率的大小,从深红色表示高概率到浅红色表示低概率。从图中可以看到,粒子对之间的联合分布在不同粒子对之间的关系上表现出明显的依赖性,这对于深入理解多体系统的物理特性具有重要意义。
此外,QBM在模拟高维复杂分布和多体相互作用方面也表现出了优势。在实验中,量子玻尔兹曼机通过量子比特之间的非对易相互作用,学习了涉及多体相互作用和高阶关联的分布,进一步展示了其在高维问题中的强大建模能力。
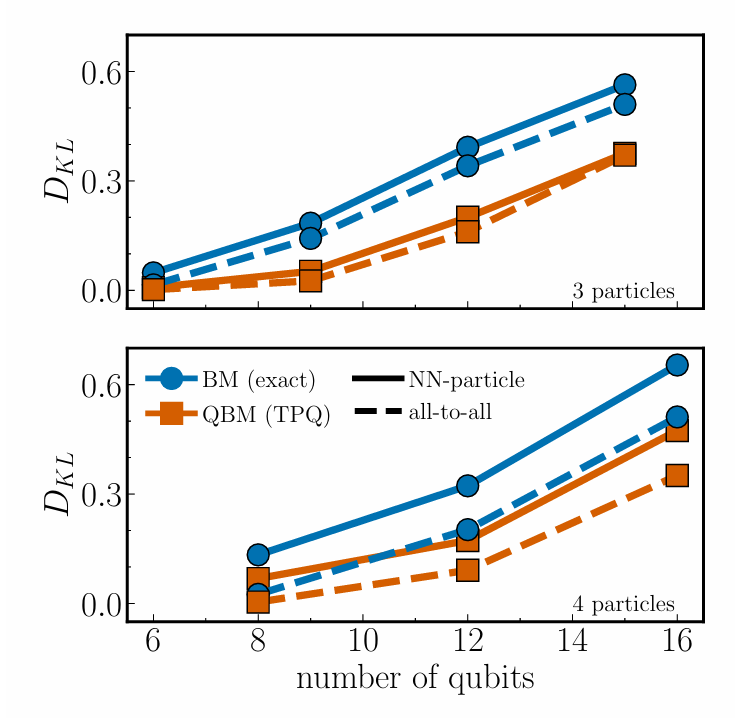
图4 经典BM与量子QBM的连接性对比
实验还将QBM与经典玻尔兹曼机及其他传统方法进行了对比,如图4,图中展示了3粒子和4粒子情况下,QBM和BM在不同连接模式下的性能差异。可以看到,在全连接模式下,QBM相比经典BM展示了较低的KL散度,特别是在粒子数较多时,QBM的表现更为突出。该图进一步说明了QBM在处理复杂数据分布时,尤其是在较高维度的情况下,具有明显的优势。
这些实验展示了量子玻尔兹曼机在模拟粒子喷流事件、学习高维数据分布和解决复杂物理问题中的应用潜力,并验证了其相较于传统模拟方法在效率和准确性方面的优势。
结论与展望
本文提出的量子玻尔兹曼机展示了其在生成高维分布中的强大能力,尤其是在粒子物理等领域。通过引入量子玻尔兹曼机,研究人员能够生成比经典玻尔兹曼机更为复杂的概率分布,尤其是在高维数据和高阶交互的情况下。随着量子计算硬件的发展,量子玻尔兹曼机有望在多个领域,如粒子物理、化学模拟等,发挥重要作用。
尽管目前量子玻尔兹曼机在小规模系统上表现良好,但其在大规模问题中的应用仍需进一步研究。未来的工作可能会集中在优化QBM的训练效率、扩展其在更大系统上的应用、以及与现有的生成模型进行比较。
论文链接:[2410.16363] Learning to generate high-dimensional distributions with low-dimensional quantum Boltzmann machines | 






















