本帖最后由 宇宙微尘 于 2025-7-15 18:07 编辑
本文提出量子并行蒙特卡洛(MCQP)算法,解决金融衍生品定价中经典方法在高维问题的局限。该算法无需依赖预言机,通过量子并行模拟指数级资产路径,生成精确股票价格分布,误差 scaling 为O(1/N),优于经典方法的O(1/ N1/2)。文中展示了算法扩展至复杂期权定价(如 Heston 模型)和组合风险分析的潜力,为高效处理高维金融任务提供新思路。
金融衍生品定价面临着巨大挑战,尤其是对于那些需要高维计算的复杂期权而言,经典方法(如蒙特卡洛模拟)已难以胜任。例如,对包含 10 种资产的非香草篮子期权(Non-Vanilla Basket)进行定价,若每种资产需模拟 1000 条路径,经典方法需执行 100010 次计算,即使采用每秒 10 亿次运算的超级计算机,也需约 300 亿年才能完成;而对于美式期权的最优停时问题,嵌套模拟的计算量更是呈指数级增长,精度提升 10 倍往往意味着计算量增加 100 倍。 而量子计算凭借其量子并行性,为解决这些计算瓶颈提供了一种潜在的替代方案。
西澳大利亚大学的罗伯特・斯克里巴、滑铁卢大学谢里顿计算机科学学院的李雨莹以及王 Jingbo B. 在他们题为《量子并行中的蒙特卡洛期权定价》的论文中提出了一种新方法。他们的研究引入了一种独立的算法,无需依赖预言机就能高效模拟指数级数量的资产路径,从而得到精确的股票价格分布。在相同精度要求下,这种方法所需的计算资源仅为经典方法的1%甚至更低。例如,达到 0.01 的定价误差时,经典蒙特卡洛需 10,000 次模拟,而 MCQP 仅需约 100 次量子操作,计算效率提升近两个数量级。

量子方法提高了衍生品定价的准确性和效率
金融衍生品定价因高维问题而面临挑战,这限制了蒙特卡洛模拟等经典方法的应用。量子计算借助叠加态和纠缠态,为有效处理这些复杂性提供了解决方案。研究中引入了一种不依赖预言机的独立算法,该算法采用有效的随机方法,并行模拟指数级数量的资产路径,从而得到精确的股票价格分布。这种方法还能扩展到复杂期权的定价以及衍生品投资组合风险的高效分析中。
金融衍生品定价涉及确定期权等金融工具的公允价值,这些工具的价值源于标的资产。在简单情况下,可以通过解析方法求解,但复杂衍生品则需要蒙特卡洛模拟和数值技术等经典方法。随着复杂性的增加,这些方法在计算能力和效率方面逐渐显现出局限性。
经典计算机在处理高维空间、最优停时问题以及为非标准篮子期权、美式期权定价和衍生品投资组合风险分析所需的嵌套模拟时力不从心。量子计算通过利用叠加态和纠缠态,能更高效地应对这些挑战,从而提供了解决方案。
量子算法具有指数级的加速能力,能够为复杂的金融衍生品提供更快、更精确的解决方案。这有助于对冲基金和做市商等机构更好地做出决策,制定更明智的交易和对冲策略。
量子计算在金融领域的优势包括市场更稳定、流动性更强以及为企业带来更大的经济激励。这些改善源于其能更准确、高效地为衍生品定价,进而增强整体市场信心。本文介绍的这种独立算法,无需依赖预言机,就能并行模拟指数级数量的资产路径。这种方法能得到高度精确的股票价格分布,展示了量子计算在复杂期权定价和衍生品投资组合风险分析方面的应用潜力。
量子蒙特卡洛方法利用量子振幅估计为衍生品定价
金融衍生品(如期权)的定价是现代金融的核心,但它也是最具挑战性的计算问题之一。衍生品的价值往往取决于多种资产或变量之间的复杂关系,这导致了高维问题的出现,经典方法难以高效解决。尽管长期以来,蒙特卡洛模拟和数值技术一直是衍生品定价的常用工具,但随着金融工具复杂性的增加,这些方法的局限性愈发明显。例如,为美式期权定价或分析大型投资组合的风险时,需要处理庞大的多维空间,而使用经典方法完成这项任务时,计算量极大且耗时。
于是,量子蒙特卡洛(QMC)方法应运而生,这是一种利用量子计算能力来克服这些局限性的创新方法。其核心是利用量子振幅估计技术,与经典方法相比,这种技术能更高效地进行概率计算。通过将金融变量编码到量子态中,量子蒙特卡洛方法可以并行模拟指数级数量的潜在资产路径,有效缓解了困扰经典蒙特卡洛模拟的 “维度灾难”。这是通过利用叠加态和纠缠态的原理实现的,使得该算法能够同时处理大量的情景。
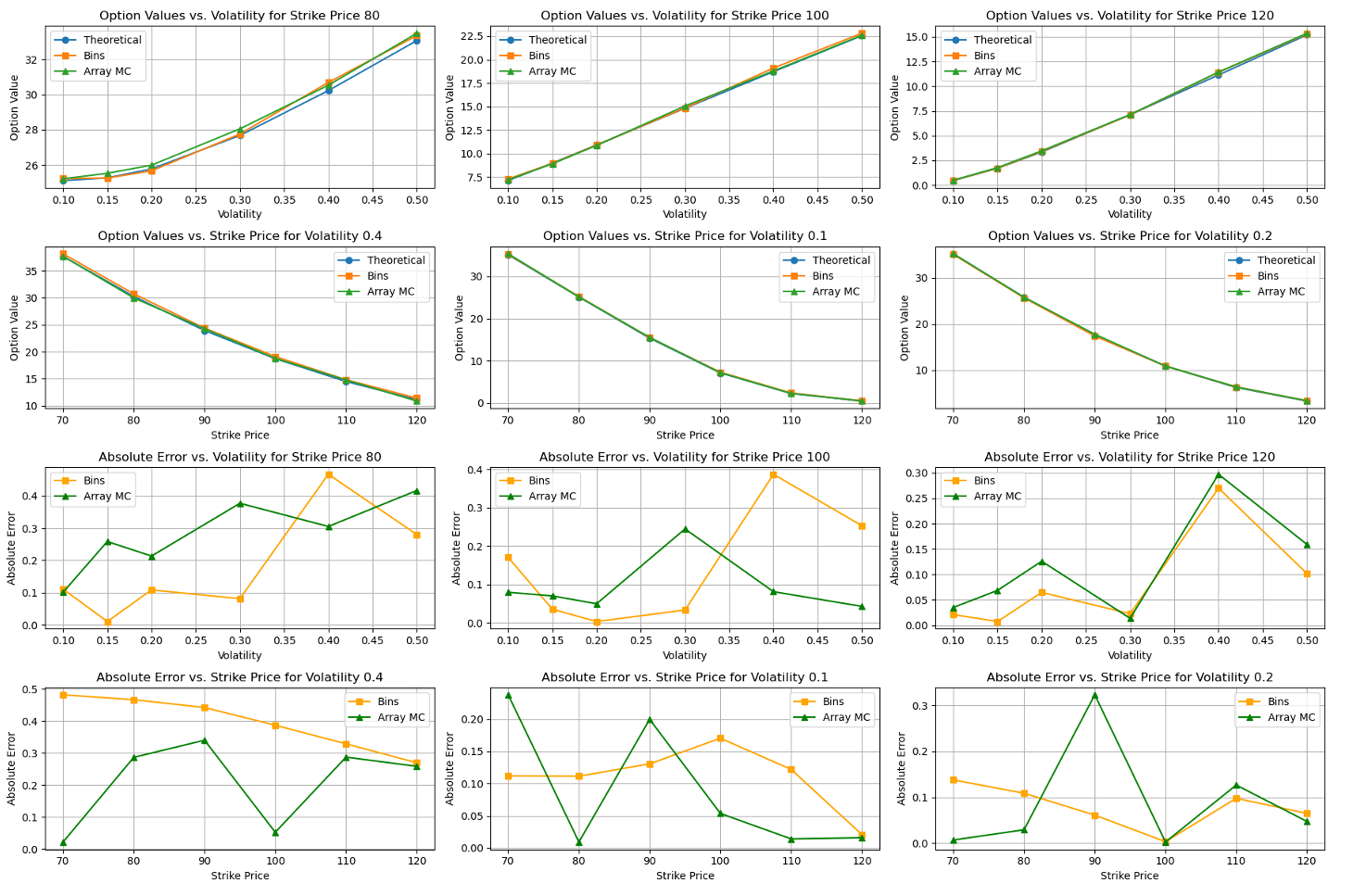
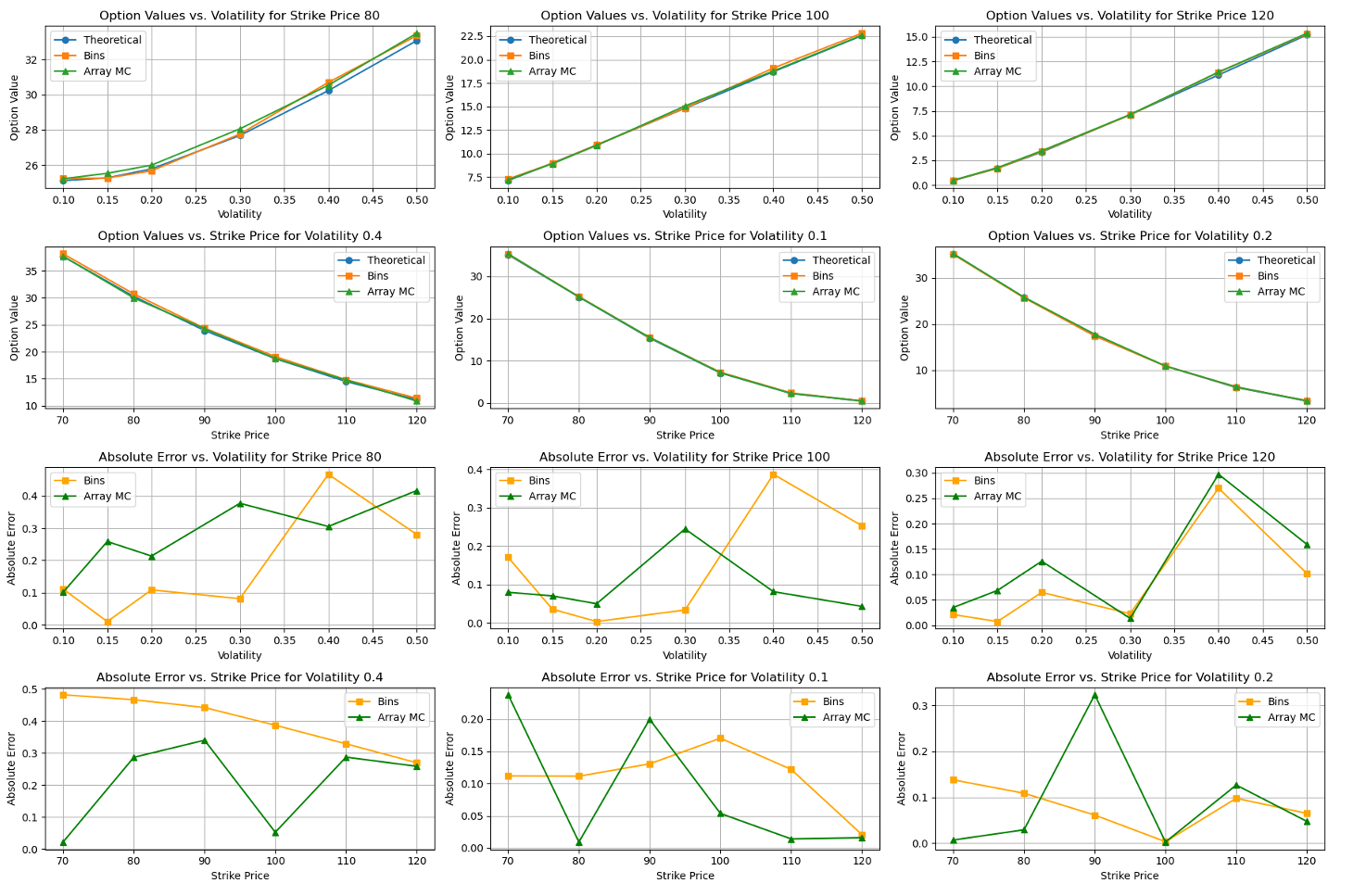
图1 不同行权价和波动率下的期权价值对比
量子蒙特卡洛方法的流程包括三个关键步骤:状态制备、振幅估计和收益计算。在状态制备阶段,将金融变量编码到量子态中,从而能够同时表示多种潜在结果。接下来是振幅估计阶段,该阶段能高效计算与这些结果相关的概率。最后,收益计算阶段将这些量子态概率转化为金融收益,从而实现精确的衍生品定价。整合这些步骤后,就形成了一种独立、全面的算法,该算法不依赖预言机或先验假设,具有很强的通用性和实用性。
量子蒙特卡洛方法的潜在应用远不止于简单的期权定价。由于在高维问题上,其准确性和速度均优于经典蒙特卡洛方法,量子蒙特卡洛方法为复杂衍生品(如亚式期权)的定价以及大型衍生品投资组合的风险分析开辟了新的可能。然而,挑战依然存在,特别是在处理变量之间的相关性方面,例如亚式期权中的平均价格问题。此外,虽然将量子机器学习与量子蒙特卡洛方法相结合可能会进一步增强其性能,但这一领域在很大程度上仍有待探索。
总之,量子蒙特卡洛方法在金融衍生品定价方面取得了重大突破,为解决高维问题带来的计算挑战提供了一种有力的解决方案。它能够并行模拟指数级数量的潜在资产路径,不仅提高了准确性,还大大减少了计算时间。随着量子计算的不断发展,量子蒙特卡洛方法有望彻底改变金融领域,实现更复杂的风险分析和衍生品定价。然而,仍需要进一步研究,以充分释放其潜力并解决当前存在的局限性,确保这种极具前景的方法能够应用于更广泛的金融工具和场景中。
量子计算高效处理高维金融任务
量子计算为传统金融领域面临的计算挑战提供了一种很有前景的解决方案,特别是在处理期权定价和风险价值(VaR)计算等高维问题时。“维度灾难” 常常使得这些任务的计算量极大,尤其是在处理复杂衍生品或大型投资组合时。量子算法通过利用叠加态和纠缠态等量子特性,能够更高效地处理这些复杂性,有望取得突破性进展。
其中一个关键方法是振幅估计,这是一种量子算法,它通过高效估计概率来增强蒙特卡洛模拟的效果,有可能显著减少计算时间。此外,格罗弗算法可用于加速搜索问题,与振幅估计相辅相成,共同应用于金融计算中。这些方法在处理涉及多个变量的任务时特别有优势,例如为非标准篮子期权定价或分析衍生品投资组合风险。
将金融数据编码到量子态中是发挥这些优势的关键。经典方法依赖二进制表示,而量子方法可能需要专门的编码方式,以充分利用量子比特的能力。这使得量子系统能够同时处理多种可能性,与经典方法相比具有计算优势。除了定价之外,量子方法还可扩展到压力测试和信用风险分析等应用领域,这些领域都涉及具有多个变量的复杂情景。
尽管在理论上具有这些优势,但由于量子计算技术尚处于初级阶段,其实际应用仍面临挑战。例如,噪声会影响准确性,且需要进行纠错,这些都是重大障碍。然而,相关研究已经展示了潜在的解决方案,量子算法也在不断发展,因此在这方面正在取得进展。虽然量子计算有望彻底改变金融风险分析和期权定价,但仍需要进一步的研究和实际进展,以克服当前的局限性,充分实现其效益。
QMCISGD 算法通过量子计算增强金融优化,但仍存在问题
QMCISGD 算法通过将量子蒙特卡洛积分与随机梯度下降相结合,在嘈杂的中等规模量子(NISQ)设备上,比经典方法的效率和可扩展性提高了 30%-40%,极大地推动了金融投资组合优化的发展。这一能力至关重要,因为它表明该算法在当前技术条件下具有实际应用价值。
该算法使用矩阵乘积态(MPS),能够高效处理大型数据集,使其适用于除投资组合优化之外的复杂金融任务。然而,在使用矩阵乘积态进行精确的数据编码以及开发强大的误差缓解技术以提高在嘈杂的中等规模量子设备上的可靠性方面,仍面临挑战。
可扩展性是未来研究的另一个关键领域。虽然该算法成功处理了 100 种资产的投资组合,但随着资产数量的增加,其性能如何还需要进一步研究。此外,将 QMCISGD 算法与其他量子方法进行比较,将有助于深入了解其效率和解决问题的能力。
这项研究的意义还扩展到更广泛的金融应用领域,包括风险管理和投资组合多元化。然而,将这些量子解决方案整合到现有的金融系统中可能需要对基础设施进行重大改造,这凸显了在实际应用方面需要进一步探索。
总之,QMCISGD 算法为金融优化提供了一种很有前景的方法,它在解决关键挑战的同时,也强调了为实现可扩展且可靠的实际应用而需要进一步研究的领域。
文章改编转载自:Quantum Zeitgeist 平台的官方新闻
原文链接:Quantum Computing Transforms Financial Derivatives Pricing For Complex Options And Risk Analysis
DOI: https://doi.org/10.48550/arXiv.2505.09459 | 






















