本帖最后由 graphite 于 2025-8-4 06:14 编辑
DVAE++ 的核心是 “重叠变换”—— 用两个重叠的连续分布近似离散潜变量,通过逆温度 β 控制离散 - 连续过渡。这一方法解决了离散变量梯度传递难题,支持玻尔兹曼机等复杂先验,还能计算解析形式的 KL 散度。实验显示,OMNIGLOT 非线性模型中,其负对数似然为 - 113.76±0.18,比 Gumbel-Softmax 低约 2.9 nats;静态 MNIST 非线性模型中,边际 ELBO 达 - 99.10±0.21,优于同类方法。结合全局离散变量(捕捉类别)与局部连续变量(刻画细节)的设计,使其在 CIFAR10 上每维度比特数低至 3.38,生成性能显著领先。
长期以来,离散潜变量因难以传递梯度信息,始终是生成式建模的难点。尽管玻尔兹曼机等模型能刻画复杂的离散分布,但传统方法要么依赖高方差的梯度估计,要么无法兼容灵活的连续松弛。
在此背景下,在2018年发表的文章《 DVAE++: Discrete Variational Autoencoders with Overlapping Transformations 》提出了DVAE++模型,为离散潜变量生成模型的训练难题提供了突破性解决方案。

01 为什么需要 “会拐弯” 的离散模型?
想象一下,你正在教 AI 识别手写数字。如果用 “非黑即白” 的离散标签来描述数字的特征,AI 可能会陷入僵硬 —— 它很难理解 “像 0 又像 6” 的模糊数字。但如果让这些离散标签 “柔和” 一点,允许中间状态存在,AI 或许能学得更灵活。
这就是离散潜变量模型面临的核心挑战:离散变量法直接传递梯度信息,导致训练困难。而现实中,离散潜变量又特别有用:它们能清晰表达 “类别”“属性” 等概念,在聚类、半监督学习中不可或缺。
早期的变分自编码器(VAE)用连续潜变量到 DVAE++ 的出现,才为离散潜变量模型找到了一条 “平滑过渡” 的新路径。
02 重叠变换让离散变量 “变软”
DVAE++的关键突破,是提出了重叠变换(overlapping transformations)—— 一种让离散潜变量 “连续化” 的巧妙方法。
什么是重叠变换?
简单说,重叠变换用两个部分重叠的连续分布来近似离散的伯努利变量(0 或 1)。比如,对于二进制潜变量 z:
当 z=0 时,用分布:
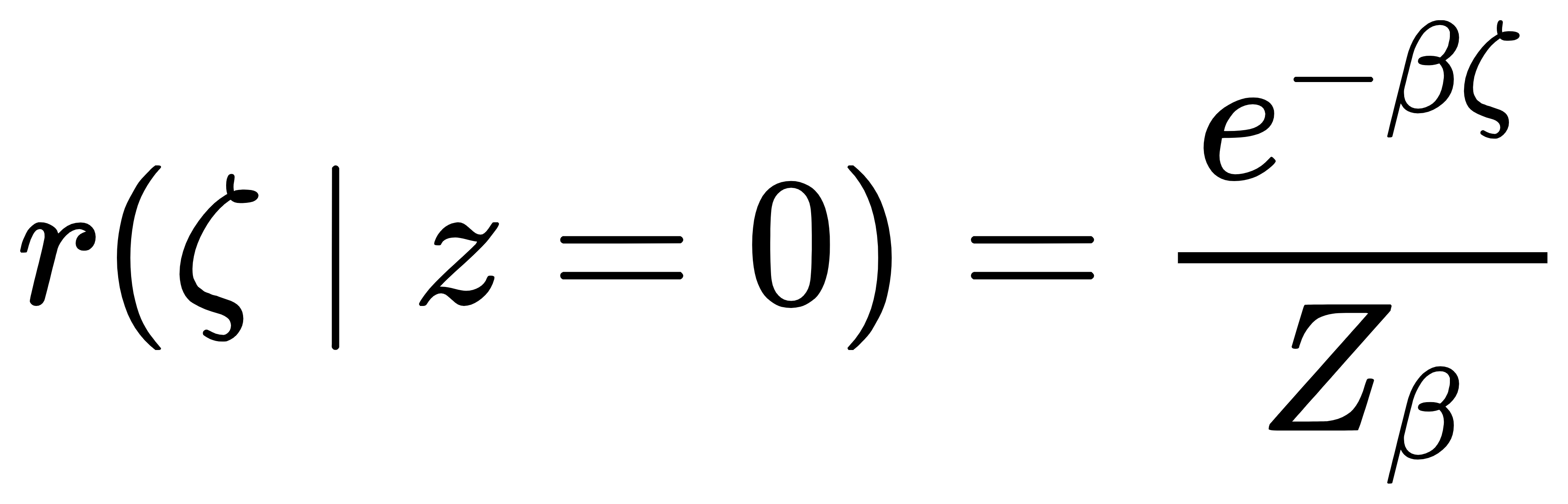
当 z=1 时,用分布:
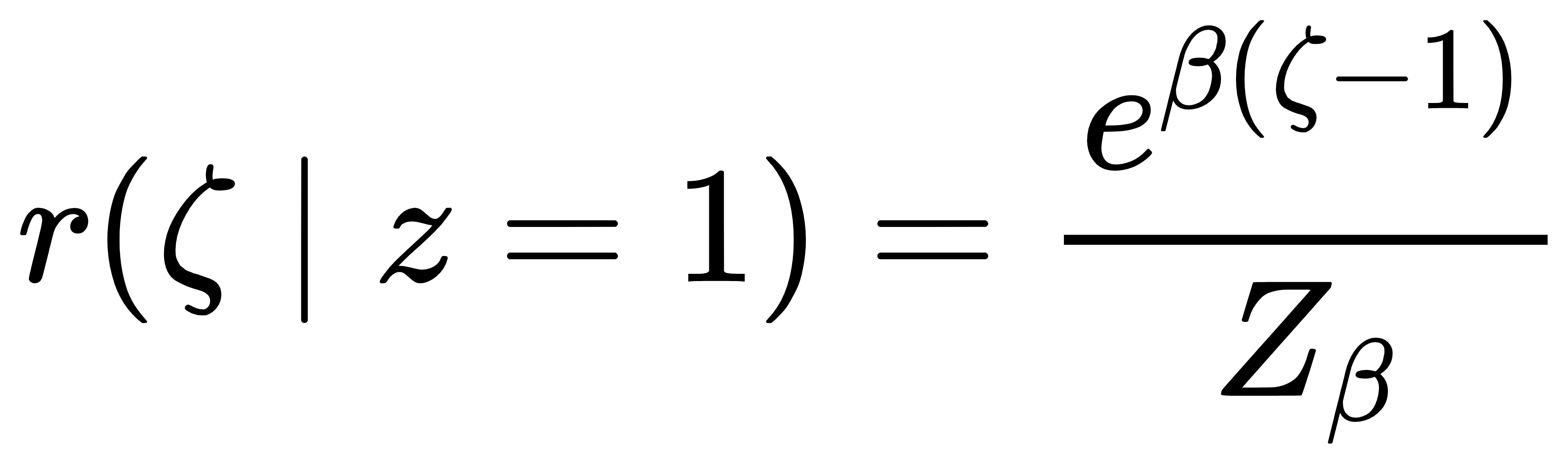
这里的 ζ 是连续辅助变量,β 是 “逆温度” 参数:β 越大,两个分布越 “尖锐”,越接近离散的 0 和 1;β 较小时,分布重叠更多,连续性更强(如图 1 左)。
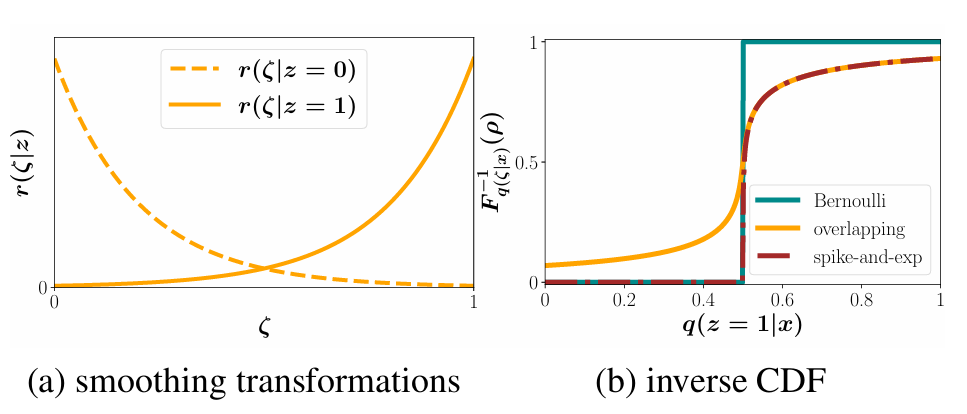
图1 平滑变换与逆 CDF 可视化
这种设计的妙处在于:既保留了离散变量的本质(β→∞时趋近离散),又能通过连续的 ζ 传递梯度,让自动微分工具可以轻松优化模型。
比传统方法好在哪?
传统方法中,z=0 时的分布是严格的 δ 函数,导致梯度计算困难。而重叠变换中,两个分布都有连续的 “尾巴”,重叠区域让梯度能顺畅传递。
对比另一种连续松弛方法 Gumbel-Softmax ,重叠变换更灵活:它不局限于分类分布,能轻松扩展到玻尔兹曼机等复杂的多元离散模型。实验显示,在 OMNIGLOT 数据集的非线性模型上,DVAE++ 的生成性能指标——负对数似然比 Gumbel-Softmax 低约 2.8 nats,优势显著。
如何用重叠变换训练模型?
DVAE++ 的训练核心是新的变分下界(ELBO)。传统 VAE 的 ELBO 为:
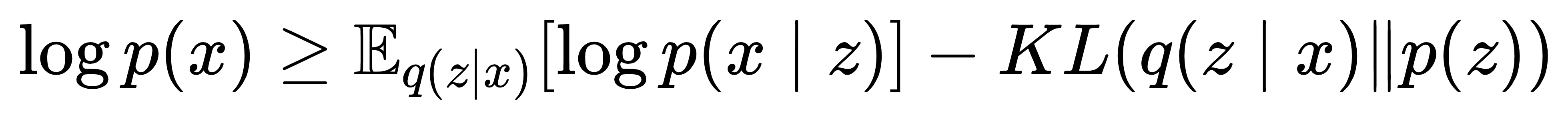
但对于离散 z,KL 项难以计算。DVAE++ 通过重叠变换,将离散 z 边际化(积分掉),得到仅含连续 ζ 的边际 ELBO:
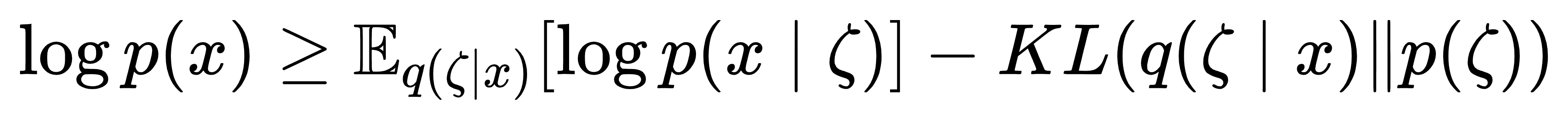
这里的关键是:KL 项可以通过解析表达式近似,无需手动编码梯度。例如,当用玻尔兹曼机作为先验时,DVAE++ 推导出的 KL 项包含熵、交叉熵等可直接计算的项,大幅简化了训练。
03 DVAE++ 的架构:全局离散 + 局部连续的 “混合高手”
DVAE++ 的强大还来自其巧妙的架构设计,它结合了两种潜变量:
全局离散潜变量(z):用玻尔兹曼机建模,捕捉 “数字类别”“场景类型” 等全局特征。
局部连续潜变量(h):用正态分布建模,捕捉 “物体姿态”“纹理细节” 等局部特征。
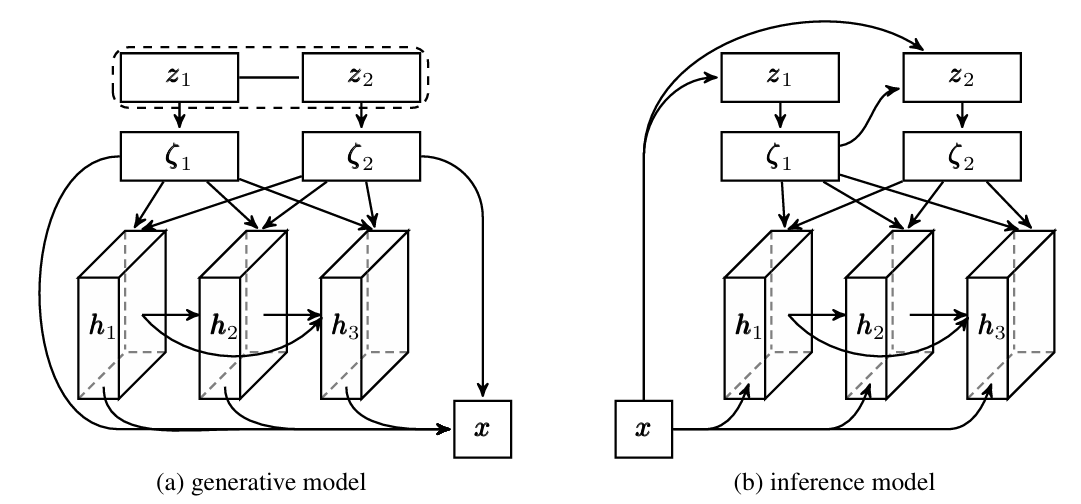
图2 DVAE++ 生成模型与推理模型架构
模型通过卷积神经网络(CNN)和残差块实现:
编码器:从图像中提取特征,依次推断全局离散变量 z 和局部连续变量 h。
解码器:基于 z 和 h,从 4×4 低分辨率逐步放大到 32×32 高分辨率,分层次生成图像。
这种设计让 DVAE++ 既能抓住数据的 “大趋势”,又能刻画 “小细节”。
04 实验验证
在多个数据集上,DVAE++ 的表现远超同期方法:
表1 DVAE++ 与基线模型的多数据集对比

在更复杂的 CIFAR-10 图像生成任务中,DVAE++ 的 “每维度比特数”(bits per dim)达到 3.37,优于没有全局离散变量的基线模型,证明了离散潜变量的价值。
生成样本也显示出其优势:同一全局潜变量生成的数字保持类别一致,而局部变量变化带来姿态差异,既稳定又灵活(如图 3)。

图3 DVAE++ 生成样本可视化
05 总结
DVAE++ 的重叠变换,本质是给离散变量一个 “缓冲带”—— 既不丢失离散的清晰性,又能享受连续变量的训练便利。这种思路不仅提升了生成模型的性能,更为需要离散潜变量的场景打开了新大门。
未来,随着更灵活的重叠变换的探索,离散潜变量模型或许会在更多领域 “大显身手”—— 从分子结构预测到文本风格迁移,我们期待这些 “会拐弯” 的离散模型带来更多惊喜。
如果还想深入探究离散变分自编码器如何突破玻尔兹曼机先验的训练瓶颈,不妨关注这篇发表于 NeurIPS 2018 的《DVAE#: Discrete Variational Autoencoders with Relaxed Boltzmann Priors》,作者也对这篇文章进行了分析:从离散到连续:DVAE# 如何突破离散潜变量模型的训练瓶颈?
论文链接:DVAE++: Discrete Variational Autoencoders with Overlapping Transformations | 








