本帖最后由 哈奇一 于 2025-8-11 14:36 编辑
在量子计算即将展现出其强大能力的今天,一个来自深度学习“史前时代”的古老模型——玻尔兹曼机(Boltzmann Machine)——意外地焕发了第二春。它因其内在的能量最小化机制与专用量子系统的物理过程存在着惊人的相似性,成为了连接两个领域的理想桥梁。

01 玻尔兹曼机的物理缘起与经典困境
要理解为何玻尔兹曼机成为量子化的热门候选,我们必须先回到它的诞生年代,重温其深刻的物理学渊源。1985年,计算机科学家杰弗里·辛顿(Geoffrey Hinton)与特里·谢诺夫斯基(Terry Sejnowski)联手提出了一种全新的、基于概率的神经网络结构,并以伟大的统计物理学家路德维希·玻尔兹曼(Ludwig Boltzmann)的名字为其命名。这并非是随意的致敬,而是因为该模型的核心数学框架,完全照搬了统计力学中描述粒子系统热平衡状态的“玻尔兹曼分布”。
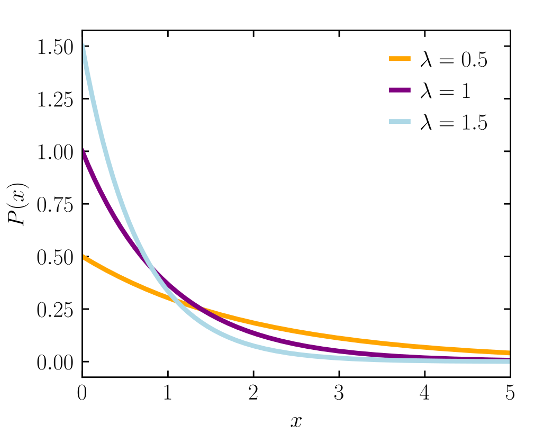
玻尔兹曼分布
辛顿本人,是后来被誉为“深度学习三巨头”之一、并荣获图灵奖和诺贝尔物理学奖的传奇人物。在长达数十年的学术生涯中,他对于“学习”的本质有着一种近乎执拗的追求。玻尔兹曼机的设计,正体现了他早期关于“学习应是系统自发行为”的哲学思考。今天,在深度学习领域的“反向传播”(Backpropagation)算法处于主流地位,它像一位严厉的教练,通过精确计算的误差梯度,强制性地逐层调整网络参数;但是玻尔兹曼机则显得更为“自然”和“民主”。
我们可以将一个玻尔兹曼机想象成一个由许多个随机“开关”(神经元)组成的网络,每个开关只有“开”(1)或“关”(0)两种状态。开关之间由不同强度的“连接线”(权重)相互连接。整个网络有一个“能量”的概念,这个能量由所有开关的状态和它们之间的连接权重共同决定。一个好的连接(正权重)会让两个都处于“开”状态的开关对系统能量有所贡献(降低能量),而一个坏的连接(负权重)则会增加能量。学习的目标,就是调整这些连接线的强度,使得当网络呈现出与训练数据(例如,手写数字的像素图)相似的“开/关”模式时,整个系统的总能量最低。
训练好的玻尔兹曼机就像一个训练有素的即兴表演剧团。你给它一个不完整的开场(比如一张被遮挡了一半的图片),它内部的演员们(神经元)会根据他们之间已经形成的默契(权重),自发地、概率性地互动和调整,最终整个剧团会稳定到一个和谐的、能量最低的整体状态,从而“脑补”出最符合情理的完整场景。
2006年前后,在深度学习的第一次浪潮中,玻尔兹曼机的一种简化版本——受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)扮演了至关重要的角色。它被辛顿用作一种无监督的预训练模块,像搭积木一样一层层地堆叠起来,构建了当时石破天惊的“深度信念网络”(Deep Belief Network, DBN),成功地解决了深度神经网络的训练难题,从而开启了现代深度学习的序幕。辛顿在多次访谈中都曾流露出对这类能量模型的偏爱,他认为这种通过系统自由演化达到稳态的学习机制,“更接近真实大脑的工作方式”。
然而,美丽的思想背后往往隐藏着残酷的计算现实。玻尔兹曼机(包括RBM)的训练过程有一个致命的阿喀琉斯之踵:高效采样问题。为了正确地调整权重,算法需要在每一步都从网络当前所定义的、极其高维的概率分布中抽取样本。在经典计算机上,这通常依赖于一种名为“吉布斯采样”(Gibbs sampling)的迭代过程。
我们可以把吉布斯采样比作在一个庞大而复杂的社交网络中进行民意调查。 调查员想要了解整个网络的普遍情绪,但不能一次性问所有人。于是他采取一种笨拙的方法:他随机找到一个人(一个神经元),询问他周围朋友(相连的神经元)的情绪,然后根据朋友们的状态来更新这个人的情绪。
他必须在网络中成千上万次地重复这个过程,让信息像流言一样慢慢地在人群中传播,直到整个网络的情绪分布达到一种动态平衡。只有在这之后,他的一次“快照”采样才被认为是有效的。这个过程极其缓慢,尤其是在网络规模巨大时,等待其“热化”并达到平衡所需的时间是天文数字。正是这个计算瓶颈,使得玻尔兹曼机在追求效率的竞赛中,逐渐被反向传播算法的光芒所掩盖。
02 伊辛模型:为玻尔兹曼机打开“穿越之门”
正当经典世界对玻尔兹曼机的采样效率束手无策时,量子世界传来了一线曙光。这道光,来自一种被称为“量子退火”(Quantum Annealing)的专用量子计算模型。而致力于将量子退火商业化的公司,如加拿大的D-Wave Systems,则成为了这场复兴运动的主要推动者。
量子退火本身并非一台通用的量子计算机,它是一台为解决特定优化问题而生的“模拟”机器。它的工作原理与物理学中的“退火”过程十分相似。在材料学中,退火是指将金属加热到高温,然后极其缓慢地冷却,让其内部的原子有足够的时间排列整齐,从而达到能量最低、结构最稳定的状态。
量子退火则在此基础上,引入了量子力学的独门绝技——量子隧穿效应(Quantum Tunneling)。
它的过程大致如下:
1、问题映射:首先,将一个优化问题(例如,寻找某个函数的最小值)编码成一个“伊辛模型”(Ising model)的哈密顿量,我们称之为“问题哈密顿量” HP。这个模型的能量格局,就精确地对应着我们优化问题的成本景观。
2、量子叠加:然后,系统被初始化到一个简单的、所有量子比特处于叠加态的基态上,这由一个“驱动哈密顿量” HD 所描述。此时,系统处于一个高能量的“量子”状态,所有可能性并存。
3、缓慢演化:接下来,退火过程开始。系统会非常缓慢地减弱驱动哈密顿量HD 的强度,同时增强问题哈密顿量 HP 的强度。整个系统的哈密顿量 H(t) 从 HD 逐渐演化为 HP。
关键的“量子魔法”就发生在这个演化过程中。在经典的退火(或优化)过程中,一个解就像一个被困在能量地貌某个山谷里的登山者。如果这是一个浅浅的局部最优山谷,他需要获得足够的能量(“温度”)才能翻越山丘,去寻找更深的山谷。而量子退火赋予了这位登山者一项超能力:他可以像一个幽灵一样,直接“隧穿”过眼前的山丘,瞬间出现在另一边的山谷里。这种隧穿的能力,使得系统有更大的机会摆脱局部最小值的束缚,最终在演化结束时“沉降”到整个地貌的全局最低能量点——也就是我们寻求的最优解。
这场量子复兴的“天作之合”在于,玻尔兹曼机的能量函数,其数学形式与量子退火机所使用的伊辛模型哈密顿量,几乎是完全一样的!这意味着,将一个玻尔兹曼机“搬”到一台量子退火机上,几乎不需要任何复杂的翻译或编译。问题的结构与机器的物理本质实现了完美的匹配。
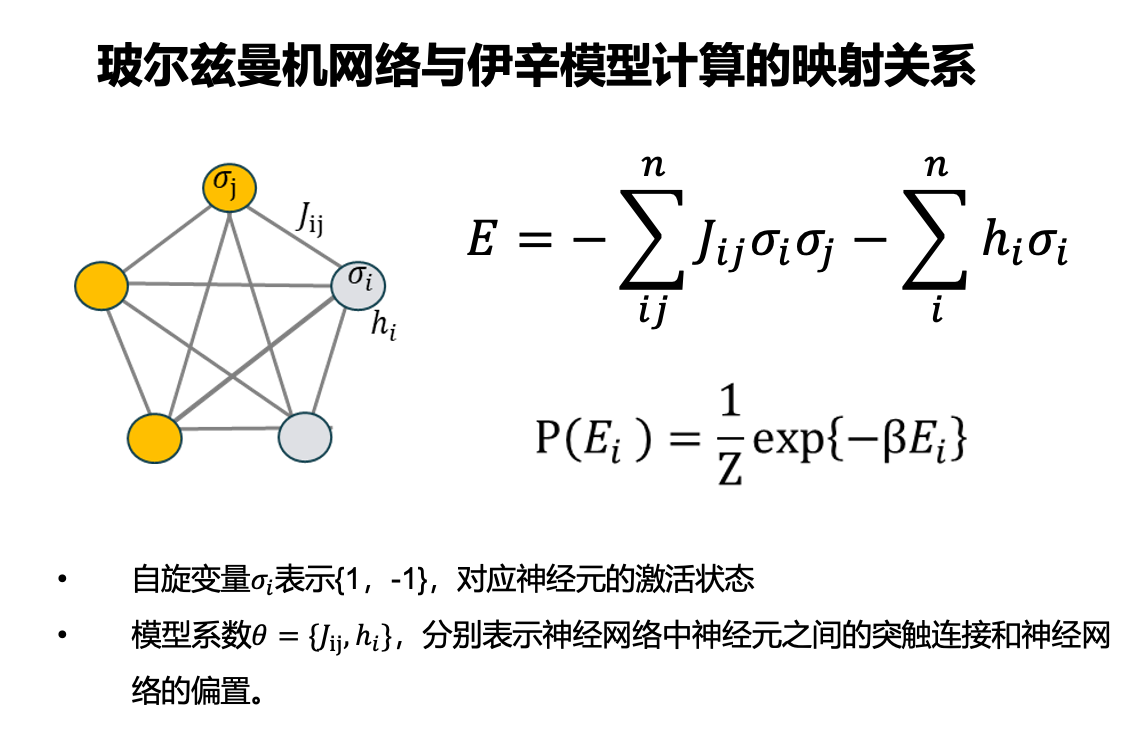
于是,量子玻尔兹曼机(Quantum Boltzmann Machine, QBM)应运而生。由D-Wave的首席科学家穆罕默德·阿明(Mohammad Amin)等研究人员率先提出和实验验证¹¹,其核心思想就是利用量子退火的过程,来代替经典玻尔兹曼机中那个慢得令人绝望的吉布斯采样。当我们将一个玻尔兹曼机的权重映射到量子退火机的耦合器上,然后启动一次退火过程,整个量子系统从叠加态到最终稳定态的自然演化,其本身就是一次从玻尔兹曼分布中进行高效采样的物理实现。

D‑Wave 的 Advantage 量子计算机
之前那个关于民意调查的比喻,在这里得到了升华。经典吉布斯采样像是在一个规矩森严的社交大厅里,人们只能挨个与邻座交谈来传递信息。而量子退火则相当于直接给这个大厅赋予了“平行宇宙”的属性。借助量子隧穿,一个人的想法可以瞬间“穿透”人群的隔阂,直接影响到远处的另一个圈子,信息的交换和平衡过程因此被极大地加速了。
在 D-Wave 等量子退火系统的支持下,研究者们已经成功地在小规模问题上展示了量子玻尔兹曼机的潜力。例如,它们被用于生成和重构简单的手写数字图像。实验表明,通过量子退火得到的样本质量,在某些情况下可以优于受限于短时间运行的经典采样方法,模型也展现出更好的泛化能力。其背后的理论是,QBM 采样的不仅仅是经典概率分布,而是一个包含了量子涨落的、更丰富的“量子玻尔兹曼分布”,这可能使其能捕捉到数据中更细微、更复杂的关联模式。
然而,从实验室的原理验证走向解决真实世界的大规模问题,QBM依然面临着重大的现实枷锁:
硬件拓扑限制:目前的量子退火芯片,其量子比特之间的连接并非“全连接”的。它们通常遵循一种稀疏的、特定的硬件拓扑图,如D-Wave的“奇美拉(Chimera)”或“飞马(Pegasus)”图。这意味着,如果要模拟一个连接复杂的玻尔兹曼机,我们必须先将问题的逻辑图“嵌入”到硬件的物理图上。这个嵌入过程往往需要将多个物理量子比特捆绑起来,共同代表一个逻辑神经元,从而造成了巨大的资源开销,极大地限制了我们能模拟的QBM的规模。
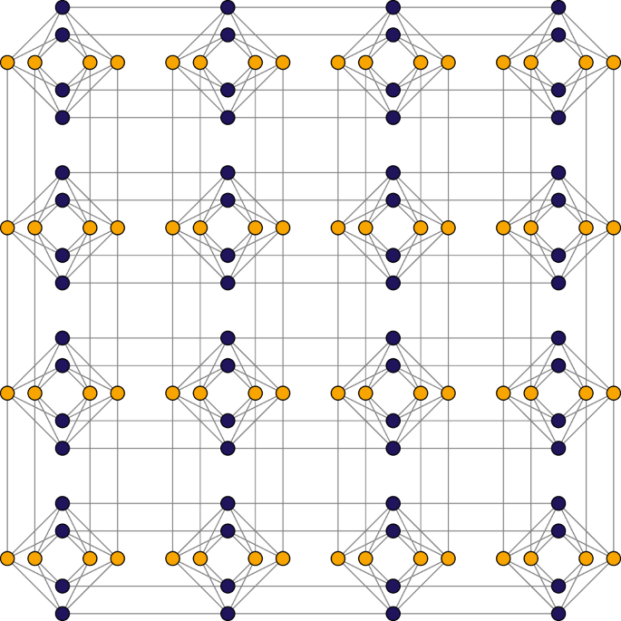
具有有限互连性的 Chimera 图
精度与噪声控制:作为模拟计算设备,量子退火机对制造过程中的微小瑕疵和环境中的热噪声非常敏感。这些模拟控制误差会影响耦合器的精确强度和量子比特的行为,使得最终的采样结果偏离理想的玻尔兹曼分布。如何精确校准和控制一个拥有数千个模拟组件的复杂量子系统,是一个持续的技术挑战。
03 相干伊辛机与玻尔兹曼机的联姻
经典的玻尔兹曼机在专用量子退火硬件上找到了复兴的希望,其核心在于两者共享了相同的物理蓝图——伊辛模型。现在,我们将目光转向另一种更为独特的专用计算设备:相干伊辛机(Coherent Ising Machine, CIM)。它更像一位科幻中掌握“原力”的绝地大师,利用光学现象中蕴含的量子特性,用激光的剑来优雅而高效地斩断那些令传统计算机头疼的组合优化难题。
相干伊辛机:以光之脉冲编织答案
要理解 CIM 的魔力,我们必须首先回到它所要解决的核心问题——求解伊辛模型。正如前述,伊辛模型不仅是统计物理学的基石,更是组合优化问题的“通用语言”。从物流配送路径规划到金融投资组合优化,再到药物分子的结构设计,无数NP-hard难题都可以被翻译成寻找一个伊辛系统最低能量状态的等价问题。因此,谁能制造出一台高效的“伊辛求解器”,谁就掌握了一把能够解锁众多行业挑战的万能钥匙。
相干伊辛机就是这样一种一台专用的、以解决伊辛问题为目标的量子物理机器。其核心部件是一种被称为“简并光学参量振荡器”(Degenerate Optical Parametric Oscillator, DOPO)的特殊激光源。与普通激光器发出的光不同,一个DOPO产生的光脉冲,其相位(可以理解为光波的振动节拍)只有两种稳定的可能性:0度或180度(π)。这两种截然相反的相位状态,天然地、完美地对应了伊辛模型中自旋(spin)的两种状态:“上”与“下”。因此,一个DOPO光脉冲,就成了一个“光学自旋”。
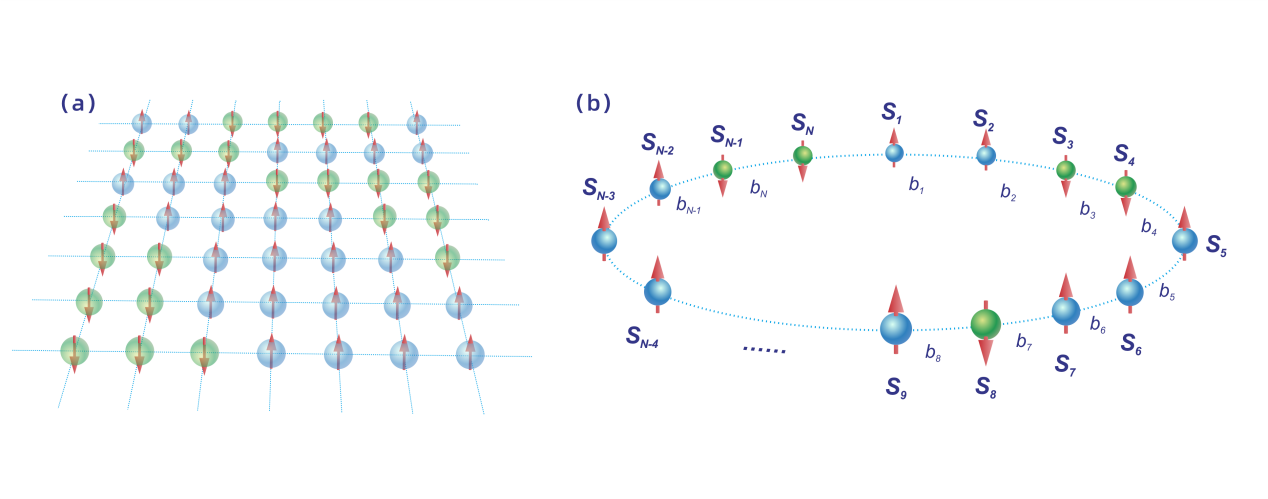
二维伊辛模型(a)和一维伊辛模型中自旋(spin)的两种状态
CIM的整个构造精巧而富有诗意。它由一圈数公里长的光纤环路构成,成千上万个DOPO光脉冲在这个环路中以光速循环往复,形成一个庞大的“光学自旋”网络。但这些自旋如何实现相互作用,以模拟伊辛模型中复杂的耦合关系(Jij)呢?这正是CIM设计中最巧妙的部分。
它采用了一种“测量-反馈”机制。在光脉冲每一次跑完一圈环路时,系统会用一个极快的探测器“偷窥”一小部分光,测量出每一个“光学自旋”的当前相位。这个信息被瞬间送入一个经典的、高速可编程的电子芯片(通常是FPGA)中。FPGA根据预设的伊辛问题耦合矩阵,迅速计算出每个自旋应该受到来自其他所有自旋的何种影响,然后将这个计算好的“影响”信号,调制到另一束光上,再注入回光纤环路,从而在下一圈循环中对相应的DOPO脉冲施加影响。
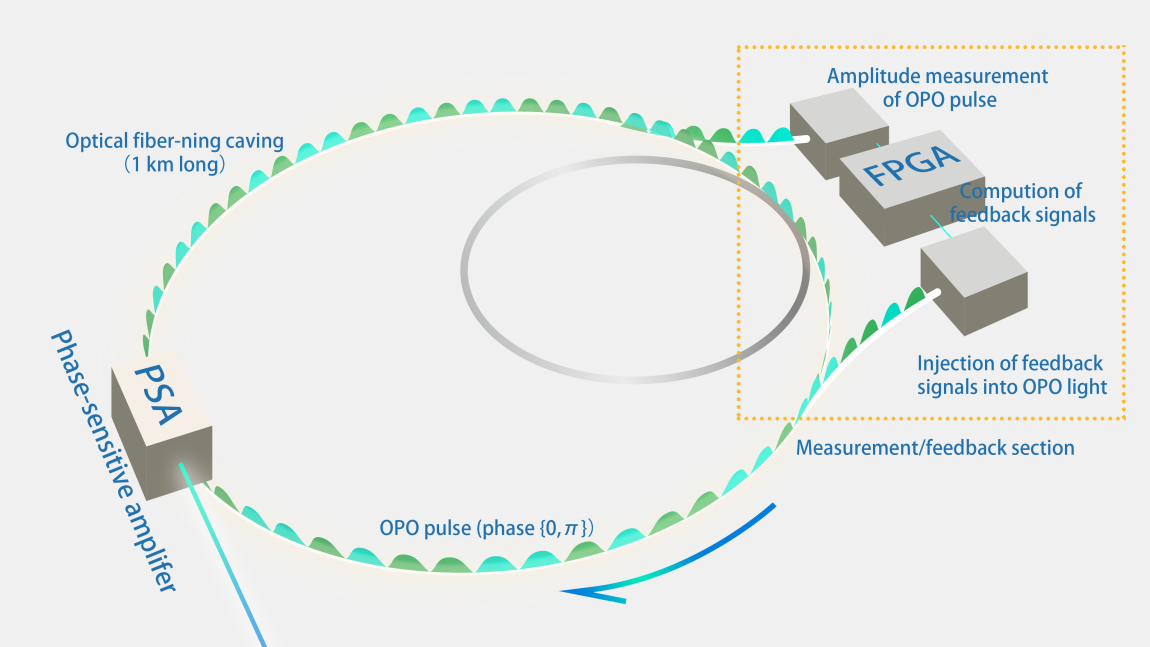
CIM的“测量-反馈”机制
我们可以用一个“万人交际舞会”的比喻来生动地理解这个过程:
舞者与舞步:光纤环路是一个巨大的圆形舞池,成千上万个DOPO光脉冲就是舞池中的舞者。每一位舞者只会跳两种舞步——向前一步(相位0)或向后一步(相位π)。
社交规则:我们要解决的伊辛问题,就是这场舞会的“社交规则”。比如,规则规定:“舞者A”希望和“舞者B”跳同一种舞步(正耦合),而“舞者C”则必须和“舞者D”跳相反的舞步(负耦合)。
舞会监督:高速的FPGA扮演着无所不知的“舞会监督”的角色。每一轮音乐(光脉冲循环一圈)结束后,监督会立刻扫视全场,看到所有舞者的舞步。然后,他根据社交规则,在下一轮音乐开始前,飞快地给每位舞者递上小纸条,上面写着建议:“A,你看B是向前走的,你也应该向前走!”或是“C,D向后走了,你最好向前走!”
寻找和谐:舞会就这样一轮轮地进行下去。在监督的快速引导下,舞者们不断调整自己的舞步,整个舞池的“社交紧张度”(即伊辛系统的总能量)迅速下降。很快,整个舞会就会自发地演化到一个全局最和谐的状态——所有舞者都采取了一种能最大程度满足所有社交规则的舞步组合。这个最终的、稳定的舞会形态,就是伊辛问题的解。
与基于超导量子比特的量子退火机相比,CIM的性质独树一帜。D-Wave的机器是一个“纯粹”的量子系统,其量子比特之间通过物理部件直接耦合。而CIM则是一个巧妙的“光-电混合”系统,其“自旋”(光脉冲)本身是宏观的经典态,它们之间的相互作用,是通过经典的电子计算来实时介导的。它之所以被称为“相干”伊辛机,并被视为“量子启发”,是因为DOPO的产生和光脉冲在环路中的演化,都深刻地依赖于光的相干性和量子噪声等底层量子光学原理。正是这些原理,赋予了CIM快速探索解空间并找到最优解的能力。
由于玻尔兹曼机的能量函数可以被直接映射为一个伊辛模型,因此一台高效的伊辛求解器,原则上就可以用来加速玻尔兹曼机的核心计算。这就像我们发现一个软件算法中最耗时的部分,恰好可以被一块专门设计的硬件加速卡(如GPU之于图形渲染)完美执行。在这里,CIM就是玻尔兹曼机梦寐以求的那块“采样加速卡”。
然而,这里有一个重要的概念需要厘清:CIM最初被设计为一个优化器(Optimizer),其目标是像一位精准的射手,直奔靶心,找到唯一的、能量最低的那个解。但是,训练玻尔兹曼机需要的却是一个采样器(Sampler),它需要像一位印象派画家,描绘出整个能量地貌的全貌,不仅要找到最低的峡谷,还要能够以正确的概率访问到那些能量稍高一些的山坡。简而言之,我们需要CIM从一个“确定性”的求解器,转变为一个“概率性”的生成器。
如何实现这种转变呢?答案是巧妙地为这台精准的机器引入可控的“噪声”,或者说“计算温度”。研究人员发现,可以通过调节CIM的运行参数来实现这一点¹²。例如,DOPO激光器的泵浦功率是一个关键旋钮。当泵浦功率远高于阈值时,光脉冲的相位被牢牢锁定在0或 π ,机器表现为一个优化器。但如果将泵浦功率调低,使其非常接近振荡的临界点,那么固有的量子噪声就会对光脉冲的最终相位产生显著影响,使其选择变得不那么确定,而是具有一定的概率性。这种内禀的量子涨落,就自然地为系统引入了“温度”。
让我们回到那个“万人舞会”的比喻。一个作为优化器的CIM,其舞会监督是一个严格的独裁者,目标是让舞会迅速定格在一个最完美的队形上。而一个作为采样器的CIM,其监督则更像一位希望派对气氛活跃的主持人。他依然会根据社交规则给出引导,但允许舞者们有一定的即兴发挥空间(噪声)。他不会强求一个单一的、静止的完美队形,而是鼓励一种动态的、和谐的“派对氛围”。
在这个氛围中,最受欢迎、最和谐的舞步组合(低能量状态)出现得最频繁,但一些稍有新意但同样可行的组合(能量稍高的状态)也有机会亮相。CIM通过一次次快速的运行,就能为我们呈现出这场“派对”的无数个精彩瞬间快照,这些快照集合起来,就构成了我们需要的玻尔兹曼分布样本。
这种光学采样方法的优势是压倒性的。CIM生成一个高质量样本所需的时间,仅仅是光脉冲在光纤环路中循环几十圈的时间,通常在微秒(百万分之一秒)量级。相比之下,经典MCMC方法为同一个复杂问题生成一个独立样本,可能需要数秒甚至数分钟。这之间,是数百万倍甚至更高的效率鸿沟。
从理论到实践:正在上演的光学加速革命
CIM与玻尔兹曼机的结合,早已不只是理论上的构想,玻色量子的一系列坚实的实验研究已经证实了其巨大的潜力,并将其应用到了实际的科学与工程问题中。
尤其是在药物设计这一前沿交叉领域,CIM也展现了其非凡的价值。药物发现的一个关键环节是“虚拟筛选”,即通过计算来预测小分子配体(潜在的药物)与靶点蛋白的结合能力。由于天然蛋白的氨基酸分布服从玻尔兹曼分布,借助物种的进化学信息和光量子计算机的玻尔兹曼采样能力,来快速学习得到蛋白序列长时的进化学信息,从而捕捉到精确的氨基酸互作关系。
这个问题可以被映射为一个复杂的能量优化问题,玻色量子进行了一项开创性的工作,利用CIM来实现玻尔兹曼采样,用于药物分子的结构优化。通过将配体分子的能量函数映射到伊辛哈密顿量,研究者在数值模拟中利用CIM高效地识别出了能量最低、最可能与靶点稳定结合的配体构型。CIM生成的样本分布严格遵循玻尔兹曼定律,使得研究者不仅能找到最优构型,还能了解其他亚优构型的概率,为药物设计提供了更全面的信息。
更有甚者,研究人员已经开始将这种光学加速器用于解决经典的监督学习任务。一项研究将一种名为“平衡传播”(Equilibrium Propagation)的算法应用在光学伊辛机上,成功地训练了一个玻尔兹曼机来识别MNIST手写数字图像,并达到了约95%的分类准确率¹⁵。这项工作巧妙地将神经网络的架构,映射到了与CIM硬件兼容的图结构上,并利用光学退火过程来执行学习中的不同阶段。这不仅证明了CIM的可扩展性,也揭示了其在构建低功耗AI系统方面的巨大潜力——光学计算相比于传统电子计算,在能效上具有天然优势。

玻色量子研制的1000比特的相干光量子计算机(CIM)
到2025年,这一领域的研究仍在飞速发展。玻色量子基于自身研制的CIM,提出了一种量子玻尔兹曼机-变分自编码器(QBM-VAE)架构,来满足概率深度学习迭代需求所需的足够量子比特数量。
概率深度学习的一个根本局限性在于它主要依赖于高斯先验假设。这一简化假设使得模型无法准确捕捉自然数据中的复杂、非高斯特性,尤其是生命科学、材料科学等领域,微观数据受测量手段影响真实的分布被层层掩饰,高斯假设会严重影响模型在科学发现中的适用性。研究组曾尝试使用基于统计物理的玻尔兹曼分布去替代高斯分布,但在传统计算机上囿于计算量巨大,难以实现。
通过引入量子玻尔兹曼机(QBM)到变分自编码器(VAE),量子变分自编码器(QBM-VAE)形成量子-经典混合生成式深度神经网络架构,可以利用CIM的量子处理器从玻尔兹曼分布中进行高效采样,从而成为能够刻画数据隐藏物理特性的深度生成模型。
在来自多个来源的数百万级单细胞数据集上应用时,QBM-VAE能够生成一个更好地保留复杂生物结构的潜在空间,在诸如“组学数据整合”、“细胞类型分类”和“轨迹推断”等关键任务上,始终优于传统的基于高斯分布假设的深度学习模型。它还提供了一个典型的例子,展示了如何将物理先验引入深度学习,以推动模型获得科学发现能力,从而突破数据限制,在大规模的科学问题上展示了深度学习中的实际量子优势,并为开发混合量子AI模型提供了可移植的蓝图。
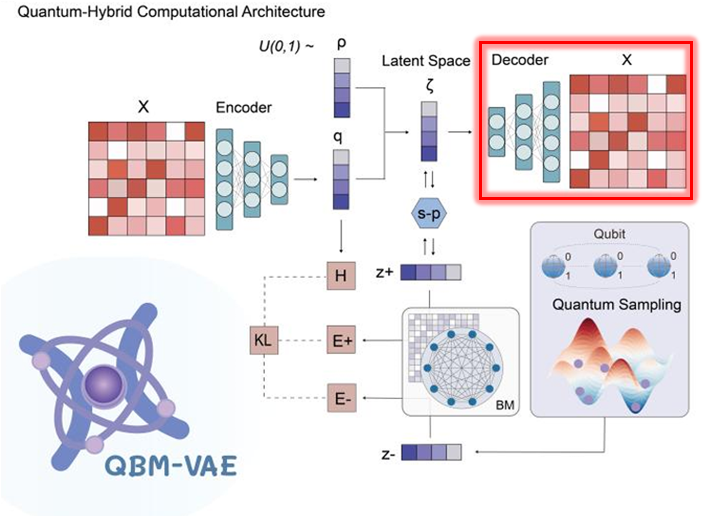
玻色量子研发的量子玻尔兹曼机-变分自编码器(QBM-VAE)
当然,通往全硬件、大规模光学玻尔兹曼机的道路并非一片坦途。硬件噪声的抑制、伊辛问题到光学耦合的精确映射、以及整个光学系统规模的进一步扩大,都是亟待攻克的工程挑战。目前的研究多数还处于数值模拟或小规模原理验证阶段。但技术的进步日新月异,随着更稳定、更大规模的DOPO网络和更精密的反馈控制技术的出现,未来可期。
相干伊辛机与玻尔兹曼机的结合,是当代科学中“物理驱动计算,计算赋能科学”这一宏大主题的完美缩影。它代表了一种深刻的融合趋势:将一个源自统计物理学的经典AI模型,与一个植根于量子光学的尖端物理设备相结合,通过硬件上的本质性突破,去解决软件算法层面长期存在的瓶颈。
它可能不会解决所有问题,但在药物发现、材料设计、金融优化以及下一代生成式AI等特定但至关重要的领域,它们或许会更早地为我们带来曙光。AI的未来,可能不仅仅是由0和1的逻辑门所构建,它的一部分,或许真的会被纯粹而相干的光所照亮。
参考文献:
Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines. Cognitive Science, 9(1), 147–169. https://doi.org/10.1207/s15516709cog0901_7
Amin, M. H., Andriyash, E., Rolfe, J., Kulchytskyy, B., & Melko, R. (2018). Quantum Boltzmann machine. Physical Review X, 8(2), 021050. https://doi.org/10.1103/PhysRevX.8.021050
Hinton, G. E. (2007). To recognize shapes, first learn to generate images. In P. C. Y. Lee (Ed.), The B.C. Lectures on Quantum Computation (pp. 229–249). World Scientific.
Cai, F., Kumar, S., Van Vaerenbergh, T., Pandraud, G., & Catthoor, F. (2020). Power-efficient Boltzmann machine training using a co-processor of coupled probabilistic bits. Neuromorphic Computing and Engineering, 1(1), 014002. https://doi.org/10.1088/2634-4386/abbd63
Honjo, T., Sonobe, T., Inaba, K., Inagaki, T., Ikuta, T., Yamada, K., & Takesue, H. (2021). 100,000-spin coherent Ising machine. Science Advances, 7(40), eabh0952. https://doi.org/10.1126/sciadv.abh0952
Inui, Y., & Yamamoto, Y. (2024). Ising and QUBO sampling by a measurement-feedback coherent Ising machine. Physical Review Research, 6(1), 013063. https://doi.org/10.1103/PhysRevResearch.6.013063
McMahon, P. L., Marandi, A., Haribara, Y., Hamerly, R., Langrock, C., Tamate, S., ... & Yamamoto, Y. (2016). A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science, 354(6312), 614–617. https://doi.org/10.1126/science.aah5178
Tatsumura, K., Yamasaki, M., & Goto, H. (2021). Boltzmann sampling from the Ising model using a numerical annealer. Scientific Reports, 11(1), 21381. https://doi.org/10.1038/s41598-021-00816-z
Terashi, K., Tatsumura, K., & Goto, H. (2022). Boltzmann sampling for structure-based virtual screening with a coherent Ising machine. Frontiers in Drug Discovery, 2, 991244. https://doi.org/10.3389/fddsv.2022.991244
引用脚注
⁹ Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for Boltzmann machines. Cognitive Science, 9(1), 147–169.
¹⁰ Hinton, G. E. (2007). To recognize shapes, first learn to generate images. In The B.C. Lectures on Quantum Computation. This sentiment is also echoed in numerous public lectures and interviews given by Hinton over the years, where he often critiques the biological implausibility of backpropagation.
¹¹ Amin, M. H., Andriyash, E., Rolfe, J., Kulchytskyy, B., & Melko, R. (2018). Quantum Boltzmann machine. Physical Review X, 8(2), 021050.
¹² McMahon, P. L., et al. (2016). A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science, 354(6312), 614–617. The concept of using pump power to control the machine's behavior between optimization and sampling is a key feature discussed in the foundational papers of the CIM.
¹³ Tatsumura, K., Yamasaki, M., & Goto, H. (2021). Boltzmann sampling from the Ising model using a numerical annealer. Scientific Reports, 11(1), 21381.
¹⁴ Terashi, K., Tatsumura, K., & Goto, H. (2022). Boltzmann sampling for structure-based virtual screening with a coherent Ising machine. Frontiers in Drug Discovery, 2, 991244.
¹⁵ Cai, F., et al. (2020). Power-efficient Boltzmann machine training using a co-processor of coupled probabilistic bits. Neuromorphic Computing and Engineering, 1(1), 014002. This work uses a simulated version of an Ising machine but demonstrates the principle of training a BM for a supervised task.
¹⁶ Inui, Y., & Yamamoto, Y. (2024). Ising and QUBO sampling by a measurement-feedback coherent Ising machine. Physical Review Research, 6(1), 013063. This recent paper provides the specific performance scaling data mentioned.
文章转载自微信公众号:量子前哨
原文链接:https://mp.weixin.qq.com/s/HvuhdHeLWklORKNGKzz2Hw | 











