本帖最后由 薛定谔了么 于 2025-10-29 01:49 编辑
时间序列数据具有时间依赖性与趋势性,因此需要结合不同的建模方法来捕捉其特性。传统的时间序列模型如ARIMA(自回归积分滑动平均模型)擅长处理线性时间序列,而现代深度学习方法如LSTM(长短期记忆网络)对非线性特征表现出色。
ARIMA与LSTM结合的基本思路
将时间序列的线性和非线性特性分离:
线性部分建模:使用ARIMA提取时间序列中的线性模式。
非线性部分建模:通过对ARIMA残差(预测误差)进行分析,用LSTM捕捉残差中的非线性结构。
结合两者的方法:

通过这种方式,可以充分利用两种模型的优势。
ARIMA与LSTM的数学公式
1. ARIMA模型
ARIMA的基本形式为:

ARIMA的目标是通过参数估计找到合适的Φ、θ和d,拟合线性部分。
2. LSTM模型
LSTM是RNN的一种改进结构,用于长时间依赖的非线性序列建模:

LSTM对ARIMA残差进行建模时,以ARIMA的预测残差作为输入,预测未来的非线性残差。
LSTM与ARIMA结合的特殊注意点
数据平稳性:ARIMA需要输入的时间序列是平稳的,可能需要进行差分处理,而LSTM对非平稳数据的处理能力更强。
残差的处理:ARIMA建模的残差必须具有非线性特征,否则LSTM的加入不会显著提高预测效果。
模型顺序性:先通过ARIMA提取线性趋势,再将残差输入LSTM。
数据规模:LSTM训练需要较大的数据规模,而ARIMA可以在小样本下表现良好。
参数调优:需要分别对ARIMA和LSTM进行优化,避免模型复杂性过高或过拟合。
案例分析
LSTM与ARIMA结合预测股票价格
1. 数据集生成
假设虚拟的股票数据集,包含每日的股票收盘价。
2. Python代码实现
代码部分包含数据生成、模型构建、训练以及可视化。
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
import torch
import torch.nn as nn
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# 数据生成
np.random.seed(42)
dates = pd.date_range('2023-01-01', periods=200)
prices = 100 + np.cumsum(np.random.normal(0, 1, 200)) # 模拟股票价格
data = pd.DataFrame({'Date': dates, 'Price': prices})
# 数据可视化
plt.figure(figsize=(10, 4))
plt.plot(data['Date'], data['Price'])
plt.title("Simulated Stock Prices")
plt.xlabel("Date")
plt.ylabel("Price")
plt.grid()
plt.show()
# ARIMA建模
train_size = int(len(prices) * 0.8)
train, test = prices[:train_size], prices[train_size:]
# ARIMA拟合
arima_model = ARIMA(train, order=(5, 1, 0))
arima_result = arima_model.fit()
arima_forecast = arima_result.forecast(steps=len(test))
# 残差提取
residuals = test - arima_forecast
# LSTM建模
scaler = MinMaxScaler()
scaled_residuals = scaler.fit_transform(residuals.reshape(-1, 1))
# 数据准备
def create_sequences(data, seq_length):
sequences = []
for i in range(len(data) - seq_length):
sequences.append((data[i:i + seq_length], data[i + seq_length]))
return sequences
seq_length = 10
sequences = create_sequences(scaled_residuals, seq_length)
X, y = zip(*sequences)
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.float32)
# LSTM模型定义
class LSTMModel(nn.Module):
def __init__(self, input_size=1, hidden_size=50, output_size=1):
super(LSTMModel, self).__init__()
self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
_, (hn, _) = self.lstm(x)
out = self.fc(hn[-1])
return out
# 模型实例化
model = LSTMModel()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# 模型训练
epochs = 50
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
outputs = model(X)
loss = criterion(outputs, y)
loss.backward()
optimizer.step()
if (epoch + 1) % 10 == 0:
print(f"Epoch {epoch+1}/{epochs}, Loss: {loss.item():.4f}")
# 预测非线性残差
model.eval()
lstm_predictions = model(X).detach().numpy()
lstm_predictions = scaler.inverse_transform(lstm_predictions)
# 综合预测
combined_forecast = arima_forecast + lstm_predictions.flatten()
# 结果可视化
plt.figure(figsize=(12, 6))
# 图1:原始价格
plt.subplot(2, 2, 1)
plt.plot(data['Date'], data['Price'], label="Original Prices")
plt.title("Original Stock Prices")
plt.legend()
# 图2:ARIMA预测
plt.subplot(2, 2, 2)
plt.plot(data['Date'][train_size:], arima_forecast, label="ARIMA Forecast", color='orange')
plt.title("ARIMA Linear Prediction")
plt.legend()
# 图3:ARIMA残差与LSTM预测
plt.subplot(2, 2, 3)
plt.plot(data['Date'][train_size:], residuals, label="ARIMA Residuals", color='red')
plt.plot(data['Date'][train_size:][seq_length:], lstm_predictions, label="LSTM Residual Prediction", color='green')
plt.title("Residuals and LSTM Predictions")
plt.legend()
# 图4:综合预测
plt.subplot(2, 2, 4)
plt.plot(data['Date'][train_size:], test, label="Actual Prices")
plt.plot(data['Date'][train_size:], combined_forecast, label="Combined Forecast", color='purple')
plt.title("Combined ARIMA + LSTM Prediction")
plt.legend()
plt.tight_layout()
plt.show()
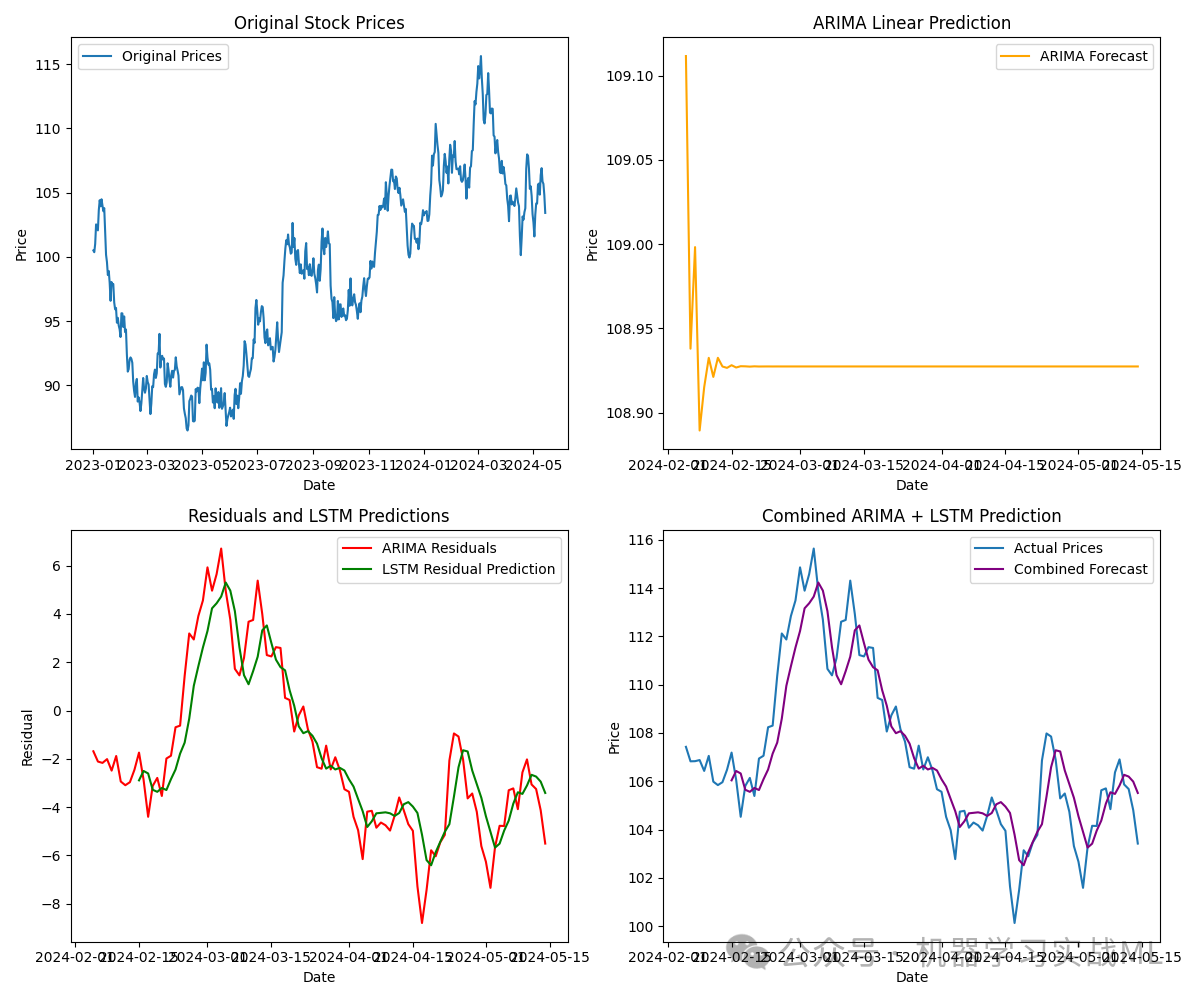
3. 数据分析图
原始股票价格趋势图:展示整体趋势,为后续建模提供参考。
ARIMA预测图:线性部分预测效果的展示。
残差分析图:显示非线性部分,并与LSTM预测进行对比。
综合预测效果图:展示ARIMA+LSTM模型的整体性能。
优化与调参
1. 模型优化点
ARIMA参数选择:通过ACF和PACF确定最佳。
LSTM超参数优化:
· 隐藏层单元数:影响记忆能力。
· 序列长度:需与数据的时间依赖特性匹配。
· 学习率与优化器:平衡收敛速度与稳定性。
混合策略调整:根据非线性程度调整ARIMA与LSTM的权重。
2. 调参流程
ARIMA调参:利用statsmodels自动选择。
LSTM调参:网格搜索或贝叶斯优化。
评估标准:RMSE、MAE等误差指标评估综合模型性能。
通过结合ARIMA与LSTM,实现了对时间序列线性与非线性特性的分离建模,提升了预测精度。表明混合模型在复杂时间序列预测中的优势。
文章改编转载自微信公众号:机器学习实战ML
原文链接:https://mp.weixin.qq.com/s/MSlNR6L7lY1qNm8UvlGYTw | 








