本帖最后由 graphite 于 2025-11-13 03:31 编辑
本文结合 Transformer 和贝叶斯优化方法,用于时间序列数据的预测与超参数调优。Transformer 模型通过自注意力机制捕捉时间序列中的长期依赖关系,而贝叶斯优化则通过高斯过程等代理模型智能地搜索最佳超参数组合,避免传统网格搜索的低效性。我们首先生成虚拟时间序列数据,并使用滑动窗口法创建训练集与测试集,然后构建了基于 PyTorch 的 Transformer 时间序列预测模型。通过 Optuna 进行贝叶斯优化,自动调节超参数,以优化模型的预测性能。实验结果展示了模型在预测精度和训练效率上的提升。
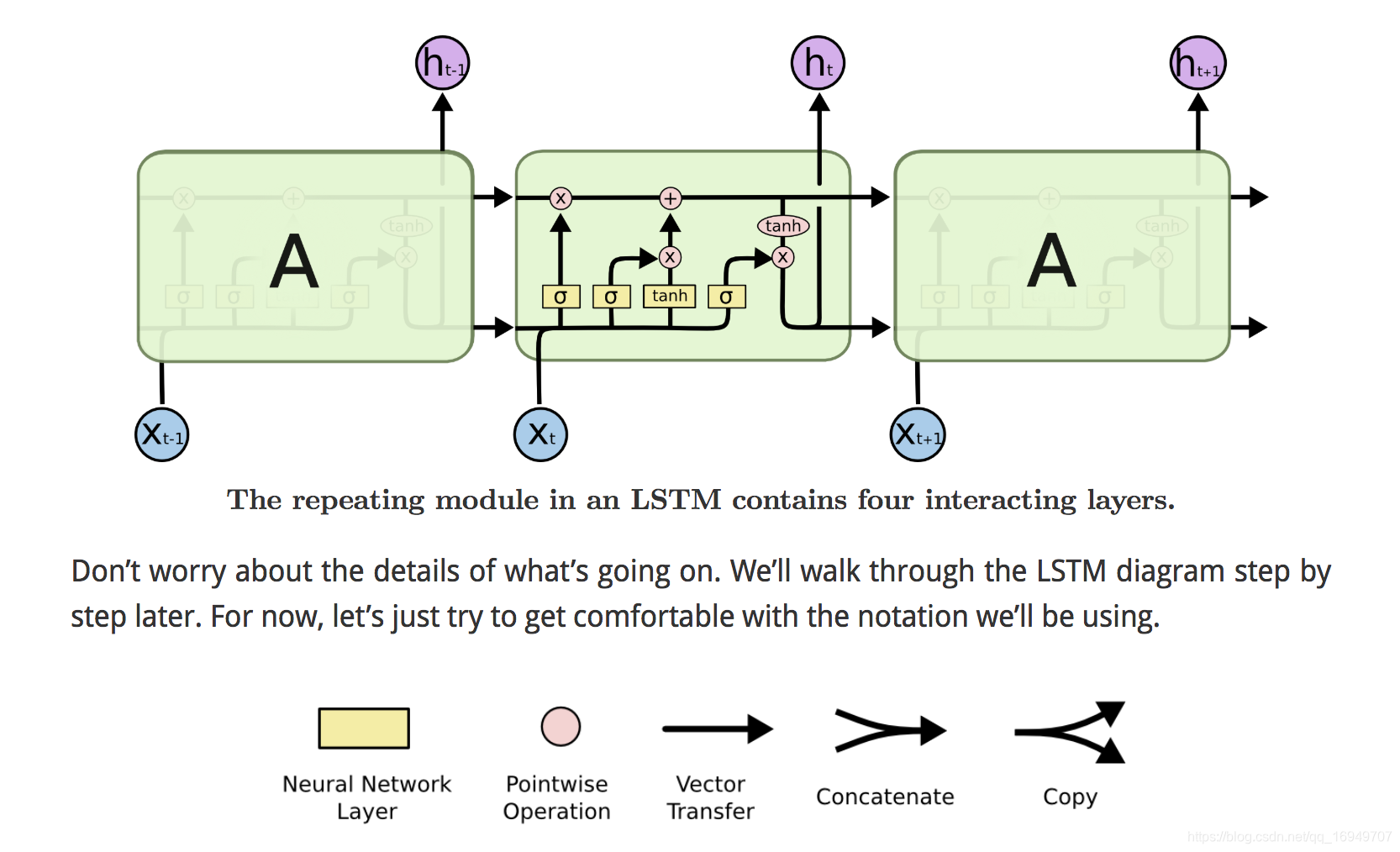
图源:网络
今天咱们来聊聊 Transformer + 贝叶斯优化:时间序列参数调优~
你可以这样理解这个组合:
Transformer 是什么?
就像大脑一样,Transformer 是一个能记住并理解时间顺序的神经网络模型。它特别擅长处理 “有顺序” 的数据,比如文本、语音、时间序列等。
如果你有一堆每天的温度、股价、销售量……Transformer 就能学会它们之间的规律,并预测未来的数值。
贝叶斯优化是干嘛的?
在训练 Transformer 时,有一堆「超参数」要设置,比如学习率、隐藏层大小、注意力头数…… 就像煮饭的火候、时间、水量,要是调得不好,饭就不好吃。
贝叶斯优化就是一个聪明的试错方法,它帮你自动找出一组最好的 “做饭方式”,也就是超参数组合,让模型效果最好。
两者结合:解决什么问题?
我们在处理时间序列时,想让 Transformer 表现好 —— 就要调它的超参数。
而用贝叶斯优化来调 Transformer 的参数,比「一个一个试」更聪明、更快。
详细原理
Part 1:Transformer 处理时间序列的原理
Transformer 最初用于 NLP(自然语言处理),但现在也常用于时间序列预测。
核心思想:自注意力(Self-Attention)
每一个时间点的数据(比如一天的销售额)都可以「注意」其他时间点的信息,从而得到一个新的表示。
输入形式:
你输入一串时间序列:
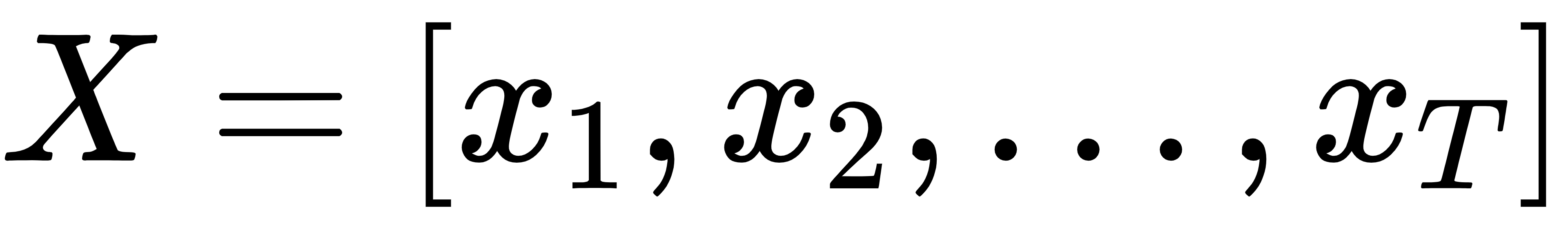
每个xt可以是多维的,例如股票的开盘价、收盘价、成交量等。
特征提取(位置编码 + 编码器)
因为 Transformer 天生不识别「顺序」,所以我们加上位置编码(Positional Encoding),告诉它数据的顺序。
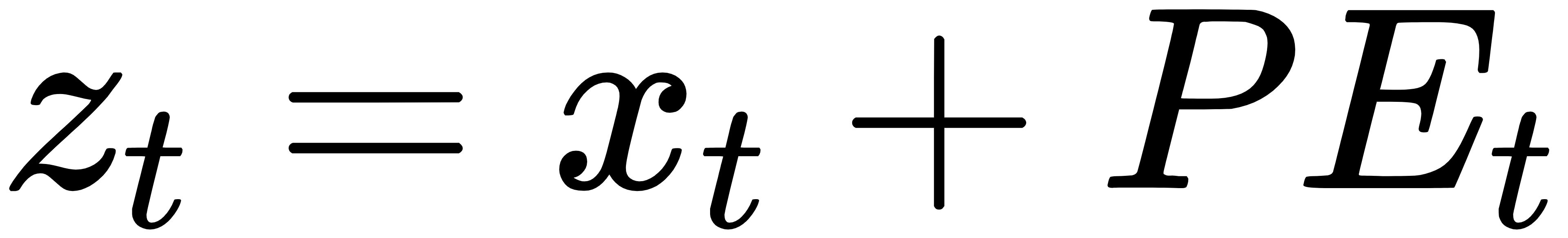
然后通过多层自注意力机制,提取序列间的深层依赖:
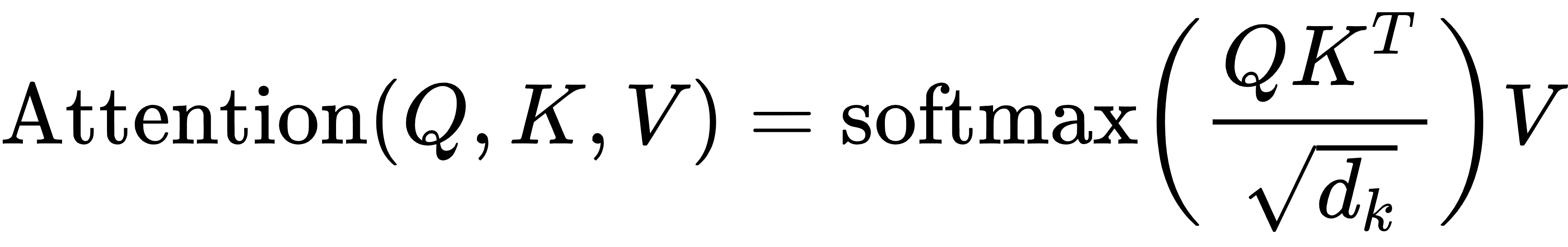
其中:
· Q、K、V 分别是 Query、Key、Value,都是从输入 z 线性变换得到的。
· dk是 Key 的维度(用于缩放)。
这样,模型就能「看全局」,而不像 RNN 那样只能从前往后处理。
最终预测:
输出通常是一个预测值,比如明天的股价或温度,取决于任务的设定。
Part 2:贝叶斯优化原理(Bayesian Optimization)
贝叶斯优化是一种基于概率模型的全局优化方法,用于在函数评估代价很高(比如训练神经网络)的情况下寻找最优参数。
思路
1.你有一个目标函数f(x):例如「某组超参数训练后的模型误差」。
2.贝叶斯优化不是直接试,而是:
· 用一个概率模型(如高斯过程)来预测这个函数可能的形状。
· 然后用这个模型来决定下次试哪个点最有希望更好。
两大组成部分
1.代理模型(Surrogate Model)
通常使用高斯过程回归(Gaussian Process, GP),它给出:
· 预测均值μ(x)
· 预测标准差σ(x)
2.采集函数(Acquisition Function)
这函数指导我们在哪里试下一个点。
一个常见的采集函数是期望改进(Expected Improvement, EI):
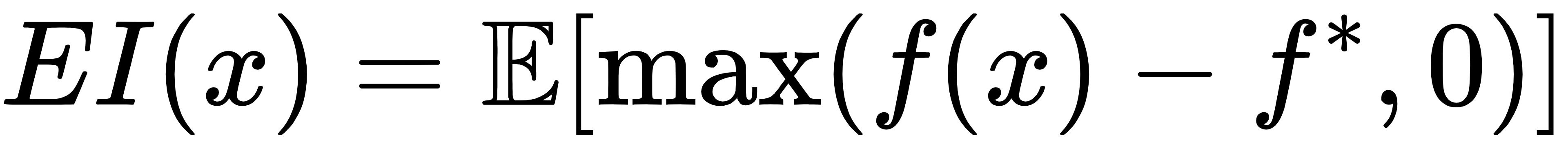
解析表达式为:
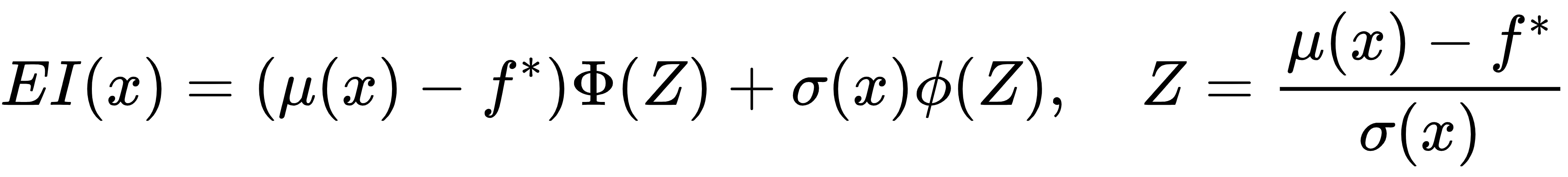
其中:
· f*当前最好的性能
· Φ标准正态分布的 CDF
· φ标准正态分布的 PDF
完整案例
咱们整个案例,包括:
· 生成虚拟时间序列数据
· 基于 PyTorch 实现的 Transformer 时间序列预测模型
· 使用贝叶斯优化调参(用 Optuna)
· 模型训练流程及评估
Transformer + Bayesian Optimization: Time Series Parameter Tuning
数据准备
这里我们用一个带有周期和趋势的虚拟时间序列。趋势和季节成分是现实中常见的时间序列特征。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 设置绘图风格
sns.set(style="whitegrid")
plt.rcParams["figure.figsize"] = (12, 6)
# 生成虚拟时间序列数据
np.random.seed(42)
time_steps = 500
# 趋势项(线性)
trend = np.linspace(0, 10, time_steps)
# 季节项(周期函数)
seasonal = 5 * np.sin(np.linspace(0, 20 * np.pi, time_steps))
# 噪声
noise = np.random.normal(0, 1.5, time_steps)
# 合成时间序列
series = trend + seasonal + noise
# 转换成DataFrame
df = pd.DataFrame({"value": series})
df["time"] = pd.date_range(start="2023-01-01", periods=time_steps, freq='D')
# 画图:时间序列整体趋势和波动
plt.plot(df["time"], df["value"], color='blue')
plt.title("Generated Time Series Data")
plt.xlabel("Time")
plt.ylabel("Value")
plt.show()
时间序列的真实样貌,包含趋势、周期和噪声,体现时间序列的复杂性。
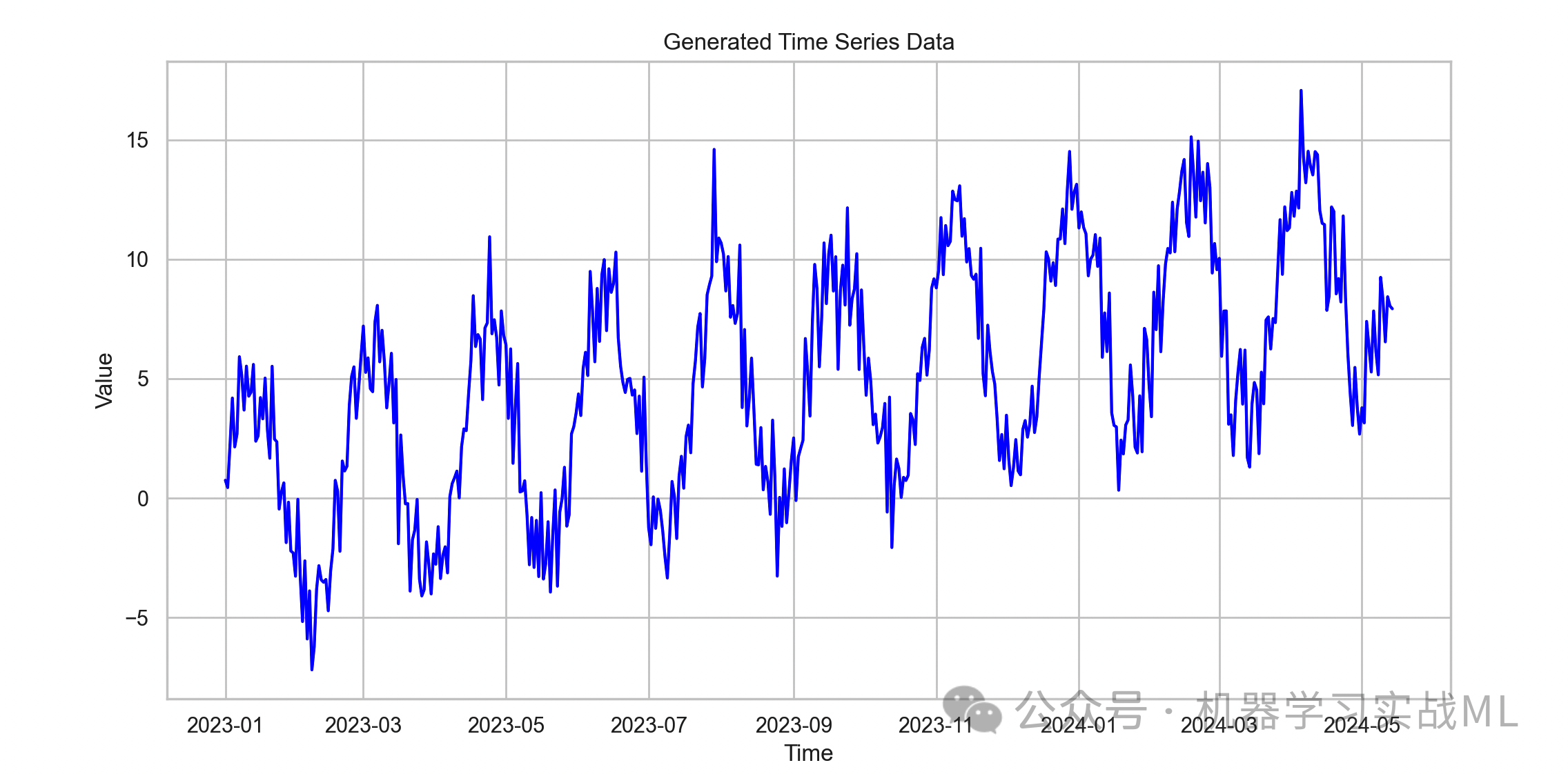
数据预处理与划分
时间序列预测不能随便划分数据集,按时间顺序分成训练集和测试集。
# 划分比例
train_ratio = 0.8
train_size = int(time_steps * train_ratio)
train_df = df.iloc[:train_size]
test_df = df.iloc[train_size:]
# 归一化(只用训练集参数)
mean = train_df["value"].mean()
std = train_df["value"].std()
train_df["value_norm"] = (train_df["value"] - mean) / std
test_df["value_norm"] = (test_df["value"] - mean) / std
# 画图:训练集与测试集划分
plt.plot(train_df["time"], train_df["value"], label="Train", color='green')
plt.plot(test_df["time"], test_df["value"], label="Test", color='red')
plt.title("Train-Test Split of Time Series")
plt.xlabel("Time")
plt.ylabel("Value")
plt.legend()
plt.show()
体现时间顺序划分,避免未来数据影响训练,防止 “数据泄露”。
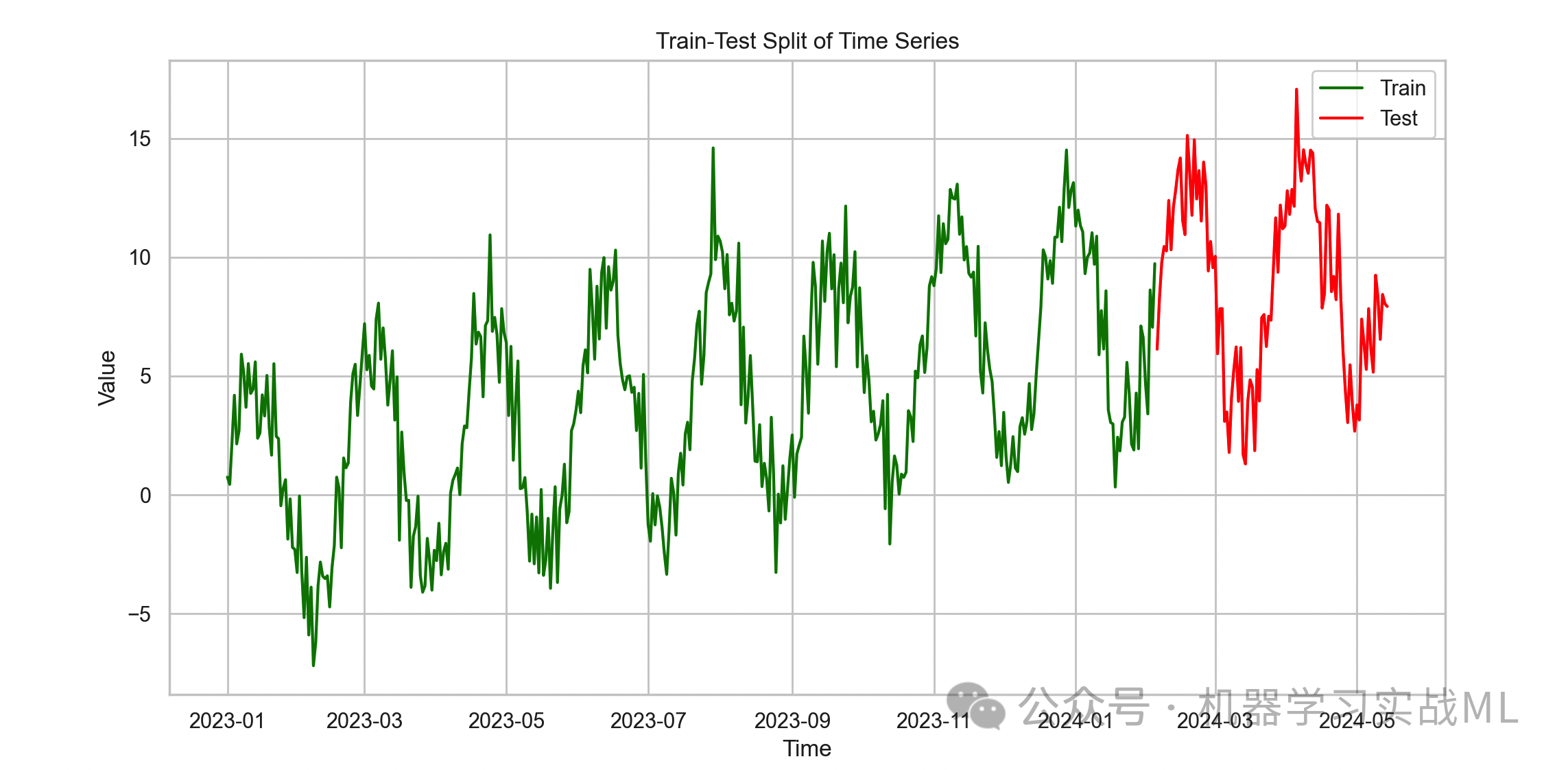
构建数据集与 Dataloader(滑动窗口)
Transformer 输入需要序列窗口,我们用滑动窗口方法制作训练样本:
· 输入窗口长度:input_window
· 预测窗口长度:output_window
我们做单步预测,output_window=1。
import torch
from torch.utils.data import Dataset, DataLoader
class TimeSeriesDataset(Dataset):
def __init__(self, series, input_window, output_window):
self.series = series
self.input_window = input_window
self.output_window = output_window
self.length = len(series) - input_window - output_window + 1
def __len__(self):
return self.length
def __getitem__(self, idx):
x = self.series[idx:idx+self.input_window]
y = self.series[idx+self.input_window:idx+self.input_window+self.output_window]
return torch.tensor(x, dtype=torch.float32), torch.tensor(y, dtype=torch.float32)
# 设置窗口大小
input_window = 30
output_window = 1
train_series = train_df["value_norm"].values
test_series = test_df["value_norm"].values
train_dataset = TimeSeriesDataset(train_series, input_window, output_window)
test_dataset = TimeSeriesDataset(test_series, input_window, output_window)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)
Transformer 模型实现
一个简易版时间序列 Transformer,核心是 Encoder 结构加线性预测头。
import torch.nn as nn
import math
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=500):
super(PositionalEncoding, self).__init__()
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1).float()
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
self.pe = pe.unsqueeze(0) # (1, max_len, d_model)
def forward(self, x):
x = x + self.pe[:, :x.size(1), :].to(x.device)
return x
class TransformerTimeSeries(nn.Module):
def __init__(self, input_dim=1, d_model=64, nhead=4, num_layers=2, dim_feedforward=128, dropout=0.1, output_dim=1):
super(TransformerTimeSeries, self).__init__()
self.d_model = d_model
self.input_proj = nn.Linear(input_dim, d_model)
self.pos_encoder = PositionalEncoding(d_model)
encoder_layer = nn.TransformerEncoderLayer(d_model=d_model, nhead=nhead, dim_feedforward=dim_feedforward, dropout=dropout)
self.transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers=num_layers)
self.decoder = nn.Linear(d_model, output_dim)
def forward(self, src):
# src shape: (batch_size, seq_len, input_dim)
src = self.input_proj(src) * math.sqrt(self.d_model) # 线性投影和缩放
src = self.pos_encoder(src)
src = src.permute(1, 0, 2) # Transformer需要(seq_len, batch_size, d_model)
output = self.transformer_encoder(src)
output = output[-1, :, :] # 取序列最后时间步的输出
output = self.decoder(output) # (batch_size, output_dim)
return output
训练函数和验证函数
def train_one_epoch(model, optimizer, criterion, dataloader, device):
model.train()
total_loss = 0
for x_batch, y_batch in dataloader:
x_batch = x_batch.unsqueeze(-1).to(device) # (B, seq_len, 1)
y_batch = y_batch.squeeze(-1).to(device) # (B)
optimizer.zero_grad()
output = model(x_batch).squeeze(-1)
loss = criterion(output, y_batch)
loss.backward()
optimizer.step()
total_loss += loss.item() * x_batch.size(0)
return total_loss / len(dataloader.dataset)
def evaluate(model, criterion, dataloader, device):
model.eval()
total_loss = 0
preds, trues = [], []
with torch.no_grad():
for x_batch, y_batch in dataloader:
x_batch = x_batch.unsqueeze(-1).to(device)
y_batch = y_batch.squeeze(-1).to(device)
output = model(x_batch).squeeze(-1)
loss = criterion(output, y_batch)
total_loss += loss.item() * x_batch.size(0)
preds.append(output.cpu().numpy())
trues.append(y_batch.cpu().numpy())
preds = np.concatenate(preds)
trues = np.concatenate(trues)
return total_loss / len(dataloader.dataset), preds, trues
贝叶斯优化调参
import optuna
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
def objective(trial):
# 超参数空间
d_model = trial.suggest_categorical("d_model", [32, 64, 128])
nhead = trial.suggest_categorical("nhead", [2, 4, 8])
num_layers = trial.suggest_int("num_layers", 1, 3)
dim_feedforward = trial.suggest_categorical("dim_feedforward", [64, 128, 256])
dropout = trial.suggest_float("dropout", 0.0, 0.3)
lr = trial.suggest_loguniform("lr", 1e-4, 1e-2)
batch_size = trial.suggest_categorical("batch_size", [32, 64])
# 构建数据加载器
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
model = TransformerTimeSeries(
d_model=d_model,
nhead=nhead,
num_layers=num_layers,
dim_feedforward=dim_feedforward,
dropout=dropout
).to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
epochs = 20
best_val_loss = float("inf")
for epoch in range(epochs):
train_loss = train_one_epoch(model, optimizer, criterion, train_loader, device)
val_loss, _, _ = evaluate(model, criterion, val_loader, device)
# 早停策略
if val_loss < best_val_loss:
best_val_loss = val_loss
return best_val_loss
study = optuna.create_study(direction="minimize")
study.optimize(objective, n_trials=30)
print("Best trial:")
trial = study.best_trial
print(f" Value: {trial.value}")
print(" Params: ")
for key, value in trial.params.items():
print(f" {key}: {value}")
用最优超参数训练最终模型
best_params = study.best_params
final_model = TransformerTimeSeries(
d_model=best_params["d_model"],
nhead=best_params["nhead"],
num_layers=best_params["num_layers"],
dim_feedforward=best_params["dim_feedforward"],
dropout=best_params["dropout"]
).to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(final_model.parameters(), lr=best_params["lr"])
batch_size = best_params["batch_size"]
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
epochs = 30
train_losses = []
val_losses = []
for epoch in range(epochs):
train_loss = train_one_epoch(final_model, optimizer, criterion, train_loader, device)
val_loss, preds, trues = evaluate(final_model, criterion, test_loader, device)
train_losses.append(train_loss)
val_losses.append(val_loss)
print(f"Epoch {epoch+1}: train loss={train_loss:.4f}, val loss={val_loss:.4f}")
数据可视化分析
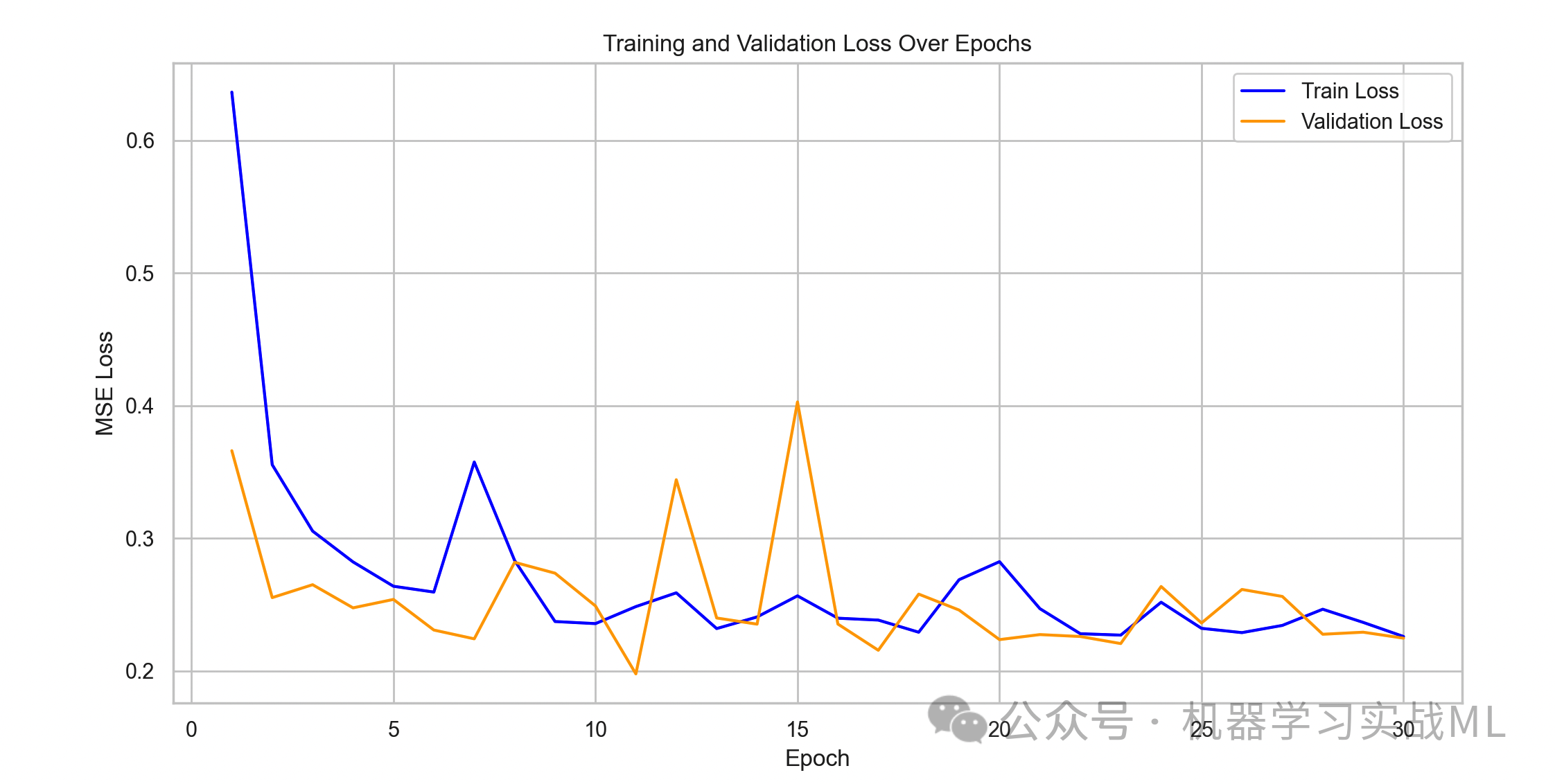
训练损失与验证损失曲线
plt.plot(range(1, epochs+1), train_losses, label="Train Loss", color='blue')
plt.plot(range(1, epochs+1), val_losses, label="Validation Loss", color='orange')
plt.xlabel("Epoch")
plt.ylabel("MSE Loss")
plt.title("Training and Validation Loss Over Epochs")
plt.legend()
plt.show()
模型训练过程,观察是否过拟合、收敛情况。
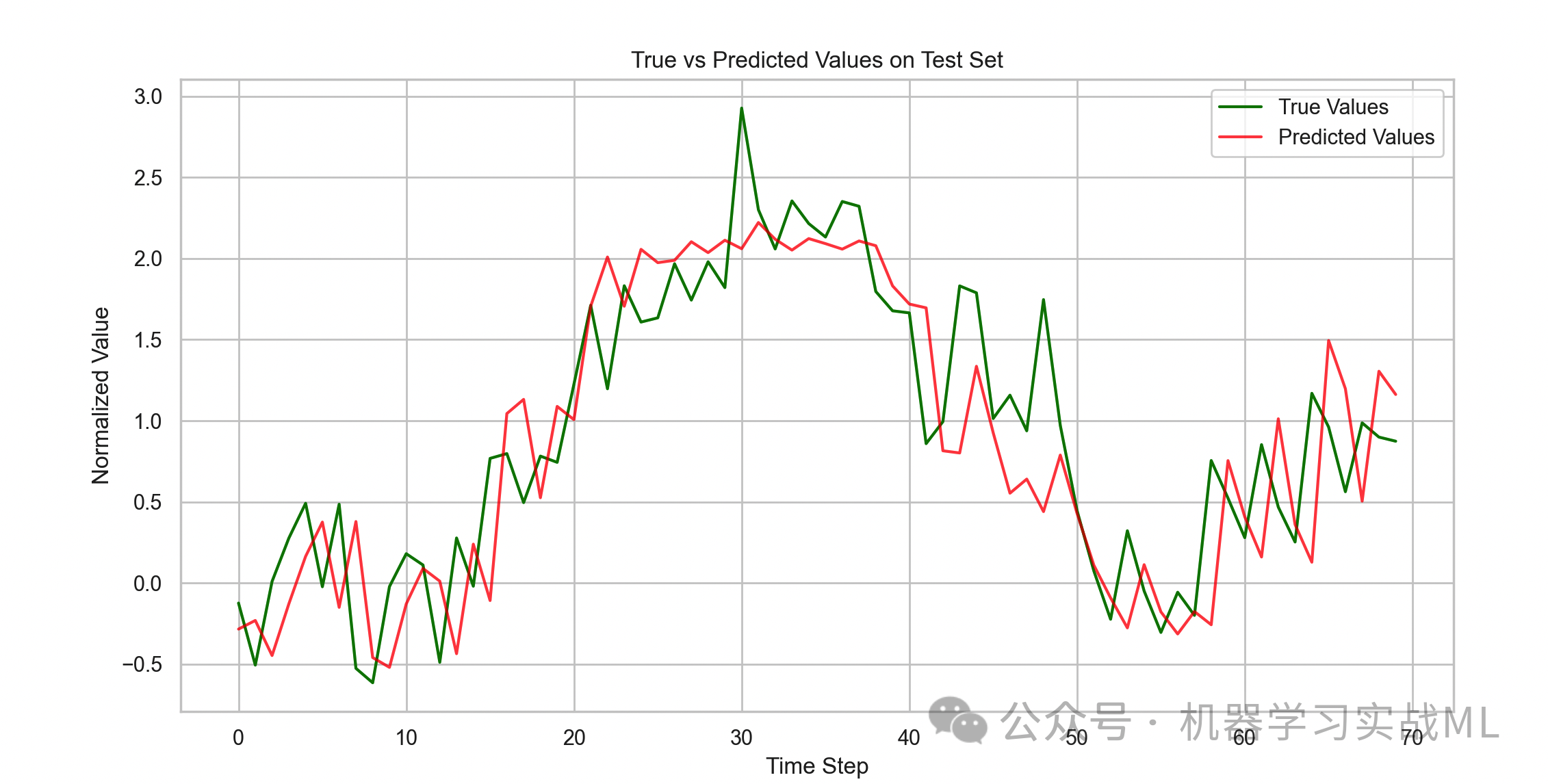
预测值 vs 真实值(测试集)
plt.plot(trues, label="True Values", color='green')
plt.plot(preds, label="Predicted Values", color='red', alpha=0.7)
plt.title("True vs Predicted Values on Test Set")
plt.xlabel("Time Step")
plt.ylabel("Normalized Value")
plt.legend()
plt.show()
直观对比预测结果和真实数据,判断模型预测的准确度。
残差(预测误差)分布直方图
residuals = trues - preds
sns.histplot(residuals, bins=30, kde=True, color='purple')
plt.title("Residuals Distribution on Test Set")
plt.xlabel("Residual (True - Predicted)")
plt.ylabel("Frequency")
plt.show()
检验预测误差是否符合正态分布,残差无偏且集中,说明模型拟合良好。

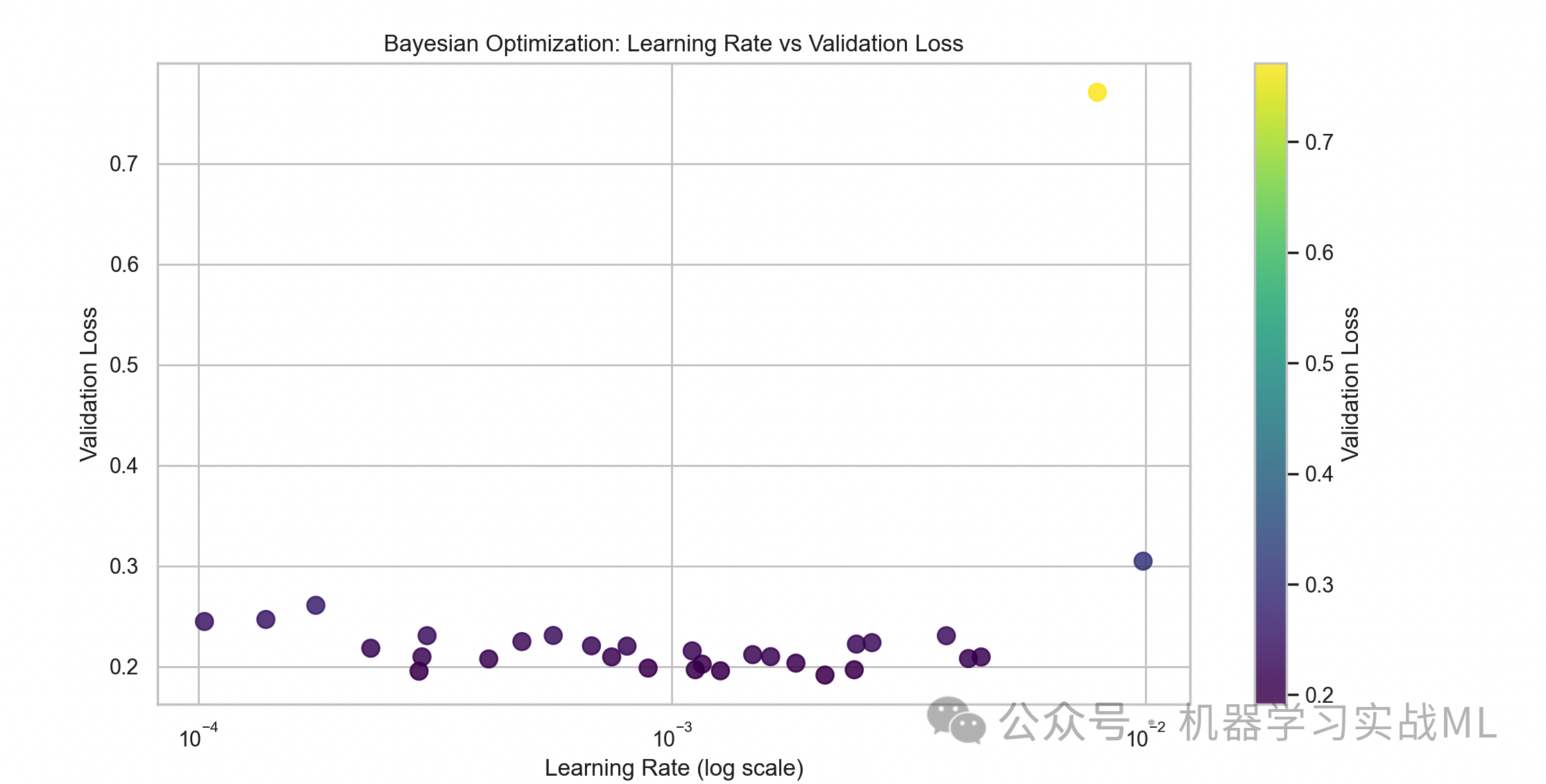
贝叶斯优化的超参数探索轨迹(学习率 vs 损失)
lr_values = [trial.params["lr"] for trial in study.trials]
loss_values = [trial.value for trial in study.trials]
plt.scatter(lr_values, loss_values, c=loss_values, cmap='viridis', s=80, alpha=0.8)
plt.xscale('log')
plt.colorbar(label='Validation Loss')
plt.xlabel("Learning Rate (log scale)")
plt.ylabel("Validation Loss")
plt.title("Bayesian Optimization: Learning Rate vs Validation Loss")
plt.show()
超参数调优过程中学习率和验证误差的关系,帮助理解哪些参数表现较好。
时间序列划分严格按照时间顺序,训练集在前,测试集在后,避免未来信息进入训练。
归一化只用训练集的均值和标准差,避免测试集信息泄露。
贝叶斯优化通过代理模型和采集函数,智能高效地搜索超参数空间。
文章改编转载自微信公众号:机器学习实战ML
原文链接:https://mp.weixin.qq.com/s/G-ypvbt0H1T3MEDvF9xkDw?scene=1 | 






















