本帖最后由 宇宙微尘 于 2025-11-23 18:43 编辑
本文探讨了Transformer-LSTM混合模型在时序数据分析中的优势与实现方法。LSTM擅长捕捉短期依赖关系,而Transformer则能高效建模长期依赖,通过将两者结合,模型能够同时处理局部细节和全局趋势,提升预测准确性。以工厂机器运行指标为例,构建了一个包含周期性、趋势、突发事件和噪声的虚拟时序数据集,设计了Transformer-LSTM混合模型进行未来数据预测。通过PyTorch实现的模型,采用多头自注意力机制提取全局特征,LSTM进一步处理时序动态,最后输出预测结果。模型训练过程中,验证了其在股票预测、气温变化和其他时序任务中的应用潜力,并通过可视化分析展示了预测结果与真实数据的对比、误差分析及模型性能评估。
咱们今天来聊聊Transformer-LSTM混合模型在时序数据分析中的应用。
先来举一个小例子:假设想预测明天的天气,你就得看看今天、昨天、前天的天气。
这是时间序列数据:数据有顺序,过去会影响未来。
现在有两种擅长处理时序的「模型大脑」:
1.LSTM:就像一个认真记笔记的学生,它会记住以前发生的事情,然后根据这些笔记来推测接下来会发生什么。
2.Transformer:更像一个聪明的总结型学生,它能一次性浏览全部内容,找出关键点、看出哪里重要,不管内容间隔多远,它都能注意到。
现在的想法是,如果把两种大脑结合起来呢?
我们就能做出一个“记得细节又看得远”的混合模型:Transformer-LSTM!
在实际应用中,比如:
· 股票价格预测
· 气温变化趋势
· 心跳、血压这种生理信号监测
· 电力负荷预测
· 交通流量分析
混合模型的表现往往比单一模型更强,因为它能兼顾局部记忆(LSTM)和全局注意力(Transformer)。
核心原理
为什么要混合?
LSTM擅长捕捉短期依赖,但遇到长期信息(比如50步以前的数据)就容易“记不住”。
Transformer擅长建模长期依赖关系,但它对局部细节(比如连续几个时间点的微妙变化)可能没LSTM敏感。
所以,混合模型 = 长期关系 + 短期记忆,两手都抓,两手都硬。
架构上怎么组合?
最常见的方式是:Transformer做特征提取器,LSTM做时间建模器
即:
1.Transformer模块先对原始输入序列进行全局建模,提取出「注意力权重分布下的重要特征」;
2.把Transformer输出结果送入LSTM,进一步利用时间上的顺序来做预测。
也可以反过来:LSTM先提取时间上下文,Transformer再去注意重要信息。
公式讲解
假设你有一个时间序列输入:
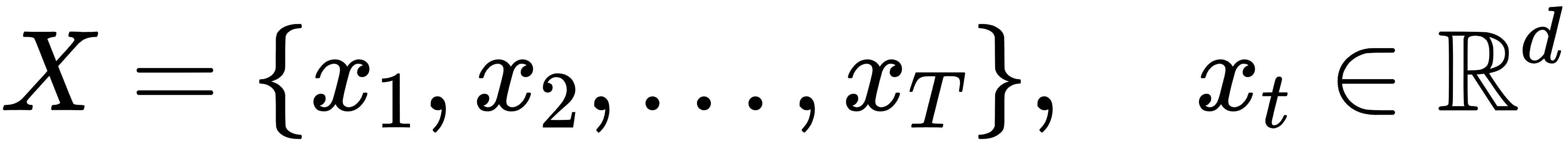
1. Transformer部分(做全局特征建模)
1)输入嵌入 + 位置编码
因为Transformer本身不考虑顺序,所以我们加上位置编码:

其中 是位置编码,比如用正弦余弦编码:

2)自注意力机制(Self-Attention)
先计算 Query、Key、Value:
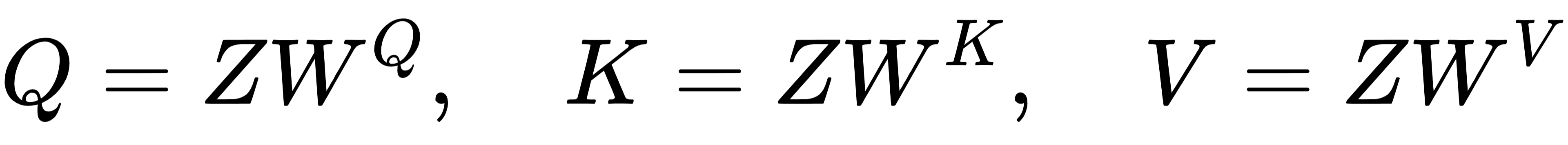
然后计算注意力权重(Softmax分数):
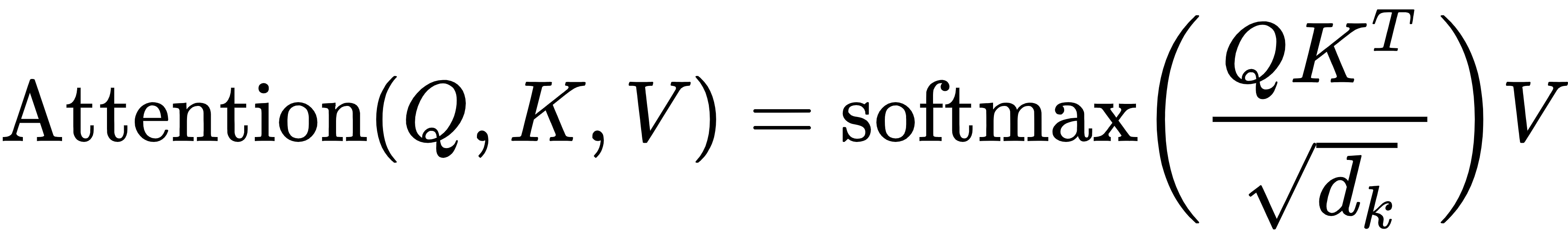
这是「谁该注意谁」的过程,能建模远距离依赖关系。
3)多头注意力(Multi-Head Attention)
多个头并行关注不同特征空间:

4)加残差 + 层归一化(LayerNorm)
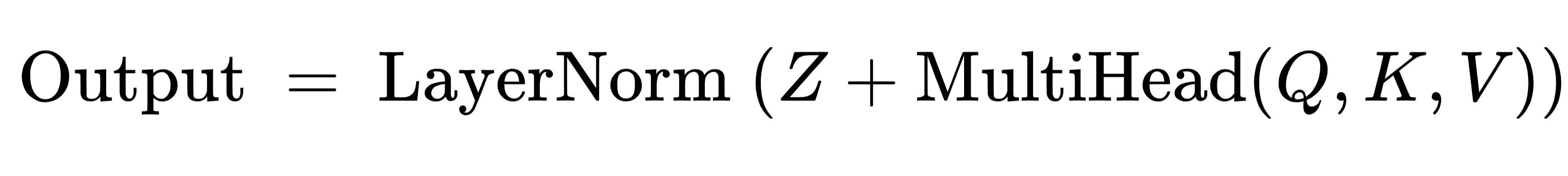
2. LSTM部分(做时序建模)
LSTM细胞在每个时间步 的操作如下:
1.遗忘门:
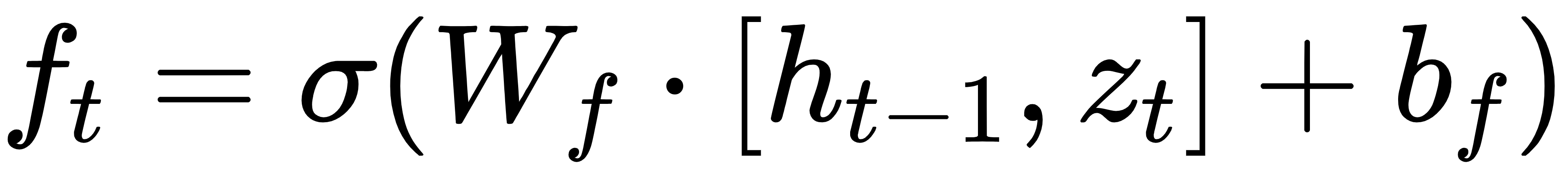
2.输入门:
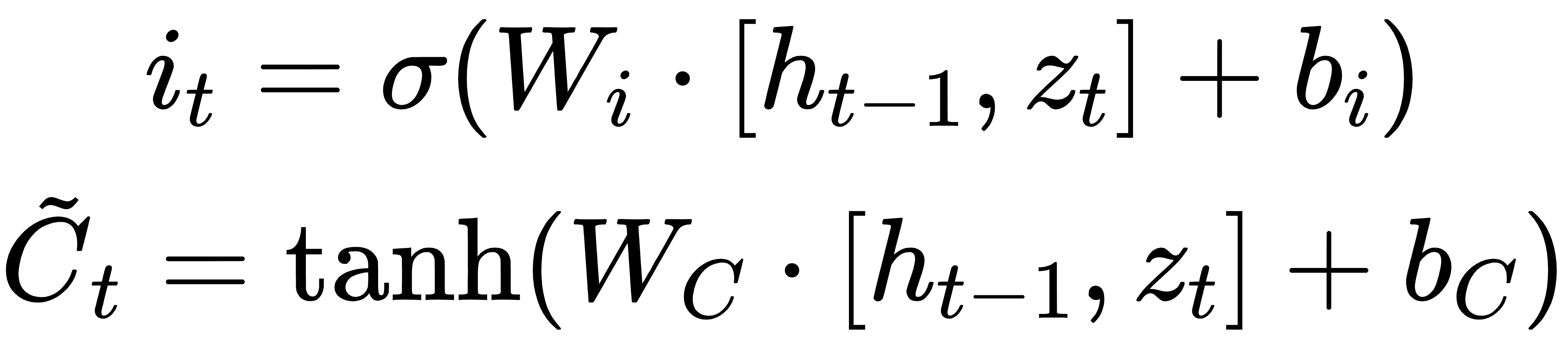
3.更新记忆状态:
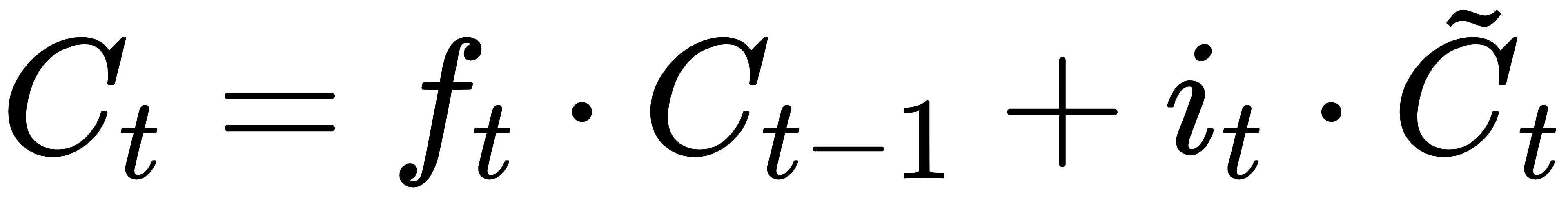
4.输出门:
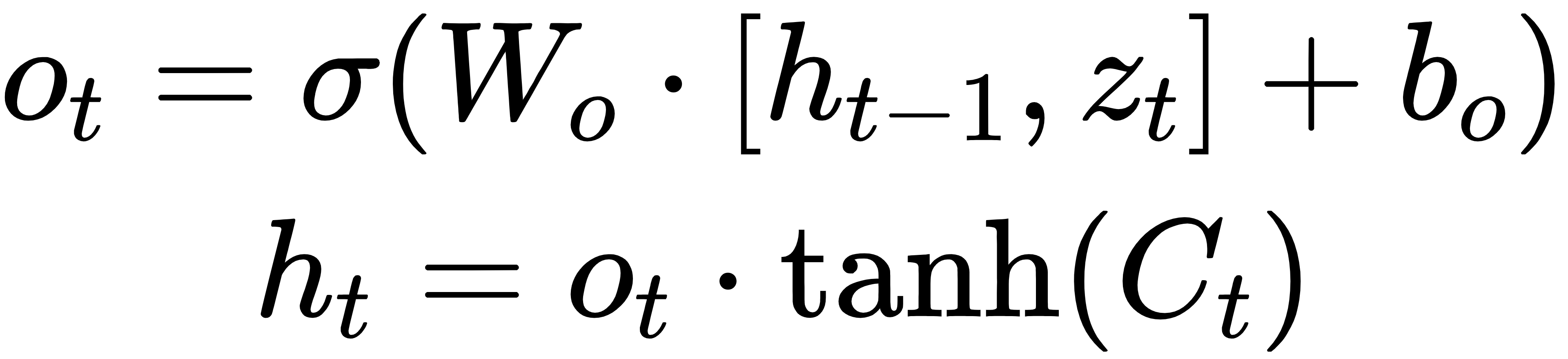
其中Zt是 Transformer 输出的向量,作为 LSTM 的输入。
3. 输出预测(例如未来一个时间点的值)
最后,将 LSTM 的最终输出 或所有时间步的输出 送入一个全连接层预测:
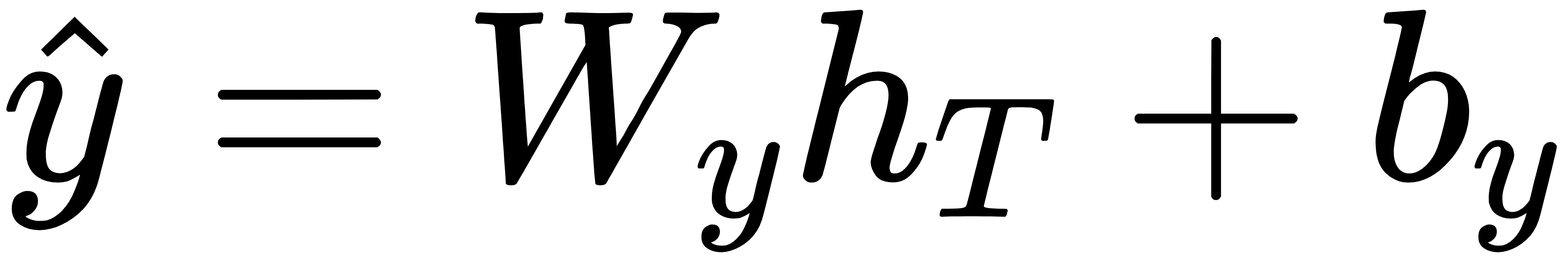
总结一句话:Transformer-LSTM混合模型 = Transformer 负责“看全局、抓重点”,LSTM 负责“按时间、记细节”,两者结合能更好地预测时序未来。
完整案例
这里,我们构造一个虚拟时序数据集,模拟某工厂机器运行指标,结合周期性与趋势成分,并叠加噪声。然后设计Transformer-LSTM混合模型预测未来数步数据。
我们构造一个时间序列数据,包含:
· 周期性成分(正弦波,反映周期震荡)
· 趋势成分(线性上升趋势)
· 突发事件(模拟异常点)
· 随机噪声
目标:预测未来10步的指标。
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.utils.data import Dataset, DataLoader
import torch.nn as nn
import torch.optim as optim
import seaborn as sns
sns.set(style="whitegrid")
# 设置随机种子
np.random.seed(42)
torch.manual_seed(42)
# 生成虚拟时序数据
time_steps = 1000
t = np.arange(time_steps)
# 生成周期性成分(两个频率叠加)
periodic = 0.5 * np.sin(0.02 * np.pi * t) + 0.3 * np.sin(0.05 * np.pi * t)
# 线性趋势成分
trend = 0.001 * t
# 突发事件:在指定位置加入异常点
anomalies = np.zeros(time_steps)
anomaly_positions = [200, 400, 600, 800]
for pos in anomaly_positions:
anomalies[pos:pos+5] += np.linspace(0.5, 1.0, 5)
# 噪声成分
noise = 0.05 * np.random.randn(time_steps)
# 最终数据
data = periodic + trend + anomalies + noise
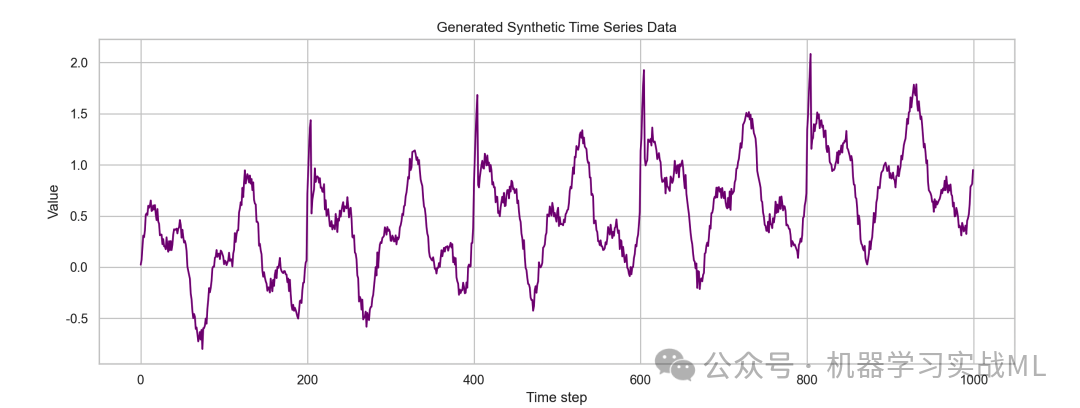
# 画出生成的时序数据
plt.figure(figsize=(14,5))
plt.plot(t, data, color='purple')
plt.title('Generated Synthetic Time Series Data')
plt.xlabel('Time step')
plt.ylabel('Value')
plt.show()
Transformer-LSTM混合模型设计
模型结构说明:
· 输入时序长度为seq_len(比如50)
· Transformer encoder层处理序列的全局依赖
· LSTM层用于进一步建模时序动态
· 最终输出未来预测的若干时间步(如预测未来10步)
设计思路:
· 输入维度:1(单一指标)
· Transformer编码器层:多头自注意力机制,捕获长依赖
· LSTM层:捕获局部动态
· 全连接层输出预测值
PyTorch模型代码:
class TransformerLSTM(nn.Module):
def __init__(self, input_dim=1, model_dim=64, num_heads=4, num_layers=2, lstm_hidden=64, lstm_layers=1, output_len=10):
super(TransformerLSTM, self).__init__()
self.model_dim = model_dim
self.input_proj = nn.Linear(input_dim, model_dim)
encoder_layer = nn.TransformerEncoderLayer(d_model=model_dim, nhead=num_heads, batch_first=True)
self.transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers=num_layers)
self.lstm = nn.LSTM(input_size=model_dim, hidden_size=lstm_hidden, num_layers=lstm_layers, batch_first=True)
self.fc = nn.Linear(lstm_hidden, output_len)
def forward(self, x):
# x shape: (batch, seq_len, input_dim)
x = self.input_proj(x) # (batch, seq_len, model_dim)
x = self.transformer_encoder(x) # (batch, seq_len, model_dim)
lstm_out, _ = self.lstm(x) # (batch, seq_len, lstm_hidden)
# 取最后一个时间步的输出
last_out = lstm_out[:, -1, :] # (batch, lstm_hidden)
out = self.fc(last_out) # (batch, output_len)
return out
数据准备与训练细节
我们设计如下:
· 输入序列长度 seq_len = 50
· 预测未来长度 pred_len = 10
· 严格时间切分训练/验证/测试集,防止数据泄露:
训练:0~700
验证:701~850
测试:851~999
4.1 Dataset封装
class TimeSeriesDataset(Dataset):
def __init__(self, data, seq_len, pred_len):
self.data = data
self.seq_len = seq_len
self.pred_len = pred_len
def __len__(self):
return len(self.data) - self.seq_len - self.pred_len + 1
def __getitem__(self, idx):
x = self.data[idx: idx+self.seq_len]
y = self.data[idx+self.seq_len: idx+self.seq_len+self.pred_len]
return torch.tensor(x, dtype=torch.float32).unsqueeze(-1), torch.tensor(y, dtype=torch.float32)
# 划分数据
seq_len = 50
pred_len = 10
train_data = data[:700]
val_data = data[700:850]
test_data = data[850:]
train_dataset = TimeSeriesDataset(train_data, seq_len, pred_len)
val_dataset = TimeSeriesDataset(val_data, seq_len, pred_len)
test_dataset = TimeSeriesDataset(test_data, seq_len, pred_len)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
4.2 模型训练
device = torch.device("cuda" if torch.cuda.is_available() else"cpu")
model = TransformerLSTM().to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
num_epochs = 30
train_losses = []
val_losses = []
for epoch in range(num_epochs):
model.train()
total_loss = 0
for x_batch, y_batch in train_loader:
x_batch, y_batch = x_batch.to(device), y_batch.to(device)
optimizer.zero_grad()
pred = model(x_batch)
loss = criterion(pred, y_batch)
loss.backward()
optimizer.step()
total_loss += loss.item() * x_batch.size(0)
avg_train_loss = total_loss / len(train_loader.dataset)
model.eval()
val_loss_total = 0
with torch.no_grad():
for x_val, y_val in val_loader:
x_val, y_val = x_val.to(device), y_val.to(device)
pred_val = model(x_val)
val_loss_total += criterion(pred_val, y_val).item() * x_val.size(0)
avg_val_loss = val_loss_total / len(val_loader.dataset)
train_losses.append(avg_train_loss)
val_losses.append(avg_val_loss)
print(f"Epoch {epoch+1}/{num_epochs}, Train Loss: {avg_train_loss:.6f}, Val Loss: {avg_val_loss:.6f}")
预测结果与可视化
测试预测:
model.eval()
preds = [ ]
targets = [ ]
with torch.no_grad():
for x_test, y_test in test_loader:
x_test = x_test.to(device)
pred_test = model(x_test).cpu().numpy()
preds.append(pred_test)
targets.append(y_test.numpy())
preds = np.concatenate(preds, axis=0) # shape (num_samples, pred_len)
targets = np.concatenate(targets, axis=0)
# 将预测拼接成连续时间序列(方便画图)
pred_series = np.zeros(len(test_data))
count_series = np.zeros(len(test_data))
for i in range(preds.shape[ 0 ] ):
start_idx = i + seq_len
pred_series[ start_idx: start_idx+pred_len] += preds[ i]
count_series[ start_idx: start_idx+pred_len] += 1
# 平均重叠预测
pred_series = np.divide(pred_series, count_series, out=np.zeros_like(pred_series) , where=count_series!=0)
可视化分析
图1:测试集真实 vs 预测序列对比
plt.figure(figsize=(16,5))
time_test = np.arange(len(test_data))
plt.plot(time_test, test_data, label='Ground Truth', color='blue')
# 彩虹渐变线绘制预测
cmap = plt.get_cmap('rainbow')
for i in range(len(pred_series)-1):
color = cmap(i / len(pred_series))
plt.plot(time_test[i:i+2], pred_series[i:i+2], color=color)
plt.title('Test Set: True vs Predicted Time Series')
plt.xlabel('Time step (test set)')
plt.ylabel('Value')
plt.legend()
plt.show()
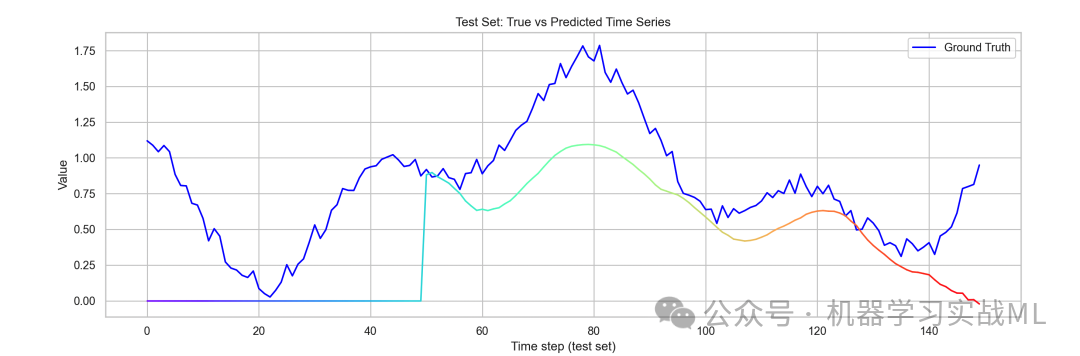
该图展示测试期间真实时间序列与模型预测的对比。蓝色是实际数据,彩虹色预测线反映模型拟合效果,颜色渐变增强视觉层次感,有助于识别预测趋势与误差区域。
图2:预测误差(残差)随时间变化
residuals = pred_series - test_data
plt.figure(figsize=(16,5))
colors = plt.cm.Reds(np.linspace(0.3, 1, len(residuals)))
plt.bar(time_test, residuals, color=colors)
plt.title('Prediction Residuals Over Time (Test Set)')
plt.xlabel('Time step')
plt.ylabel('Residual (Predicted - True)')
plt.show()
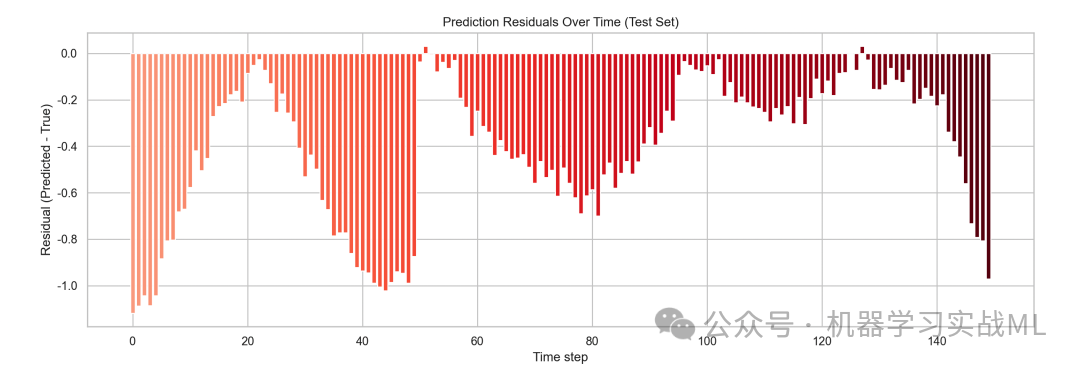
此条形图显示模型在每个时间点上的预测误差,红色渐变体现误差大小和方向,便于快速定位误差峰值和异常点,分析模型缺陷和异常事件预测表现。
图3:训练与验证损失曲线
plt.figure(figsize=(10,6))
plt.plot(train_losses, label='Train Loss', color='blue')
plt.plot(val_losses, label='Validation Loss', color='orange')
plt.title('Training and Validation Loss Over Epochs')
plt.xlabel('Epoch')
plt.ylabel('MSE Loss')
plt.legend()
plt.show()
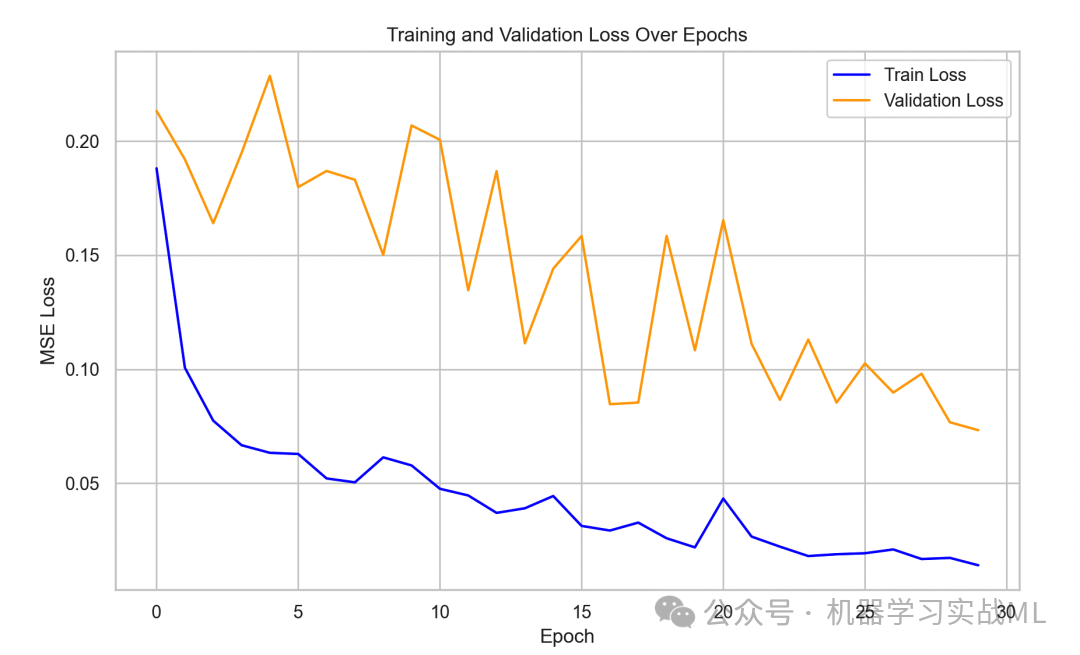
该图展示模型训练过程中的损失变化,蓝色曲线为训练误差,橙色曲线为验证误差。趋势收敛和过拟合情况清晰展现,有助于评估训练过程及模型泛化能力。
图4:预测与真实值分布对比(核密度估计)
plt.figure(figsize=(10,6))
sns.kdeplot(test_data, label='True Distribution', color='green', fill=True, alpha=0.3)
sns.kdeplot(pred_series, label='Predicted Distribution', color='purple', fill=True, alpha=0.3)
plt.title('Distribution of True vs Predicted Values (Test Set)')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()
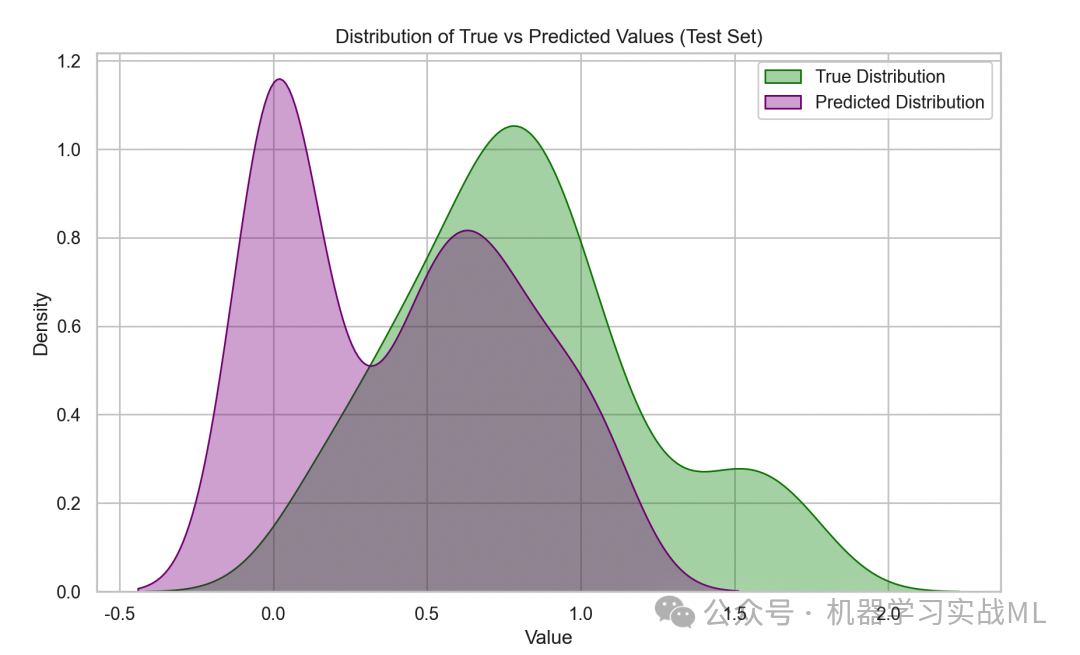
通过核密度估计对比真实值和预测值的分布形态,紫色和绿色填充区展示数据密度,能直观反映模型对数据整体趋势和波动范围的捕捉程度。
文章改编转载自微信公众号:机器学习实战ML
原文链接:https://mp.weixin.qq.com/s/ilCglF-oB8VEptap3rFVPw | 






















