本帖最后由 Akkio 于 2026-1-16 02:46 编辑
传统蒙特卡洛方法(如 HMC 等)在格点场论采样中面临临界减速、符号问题及反问题等核心挑战,亟需可统计改进、可扩展且能提升性能的替代采样方案。生成式模型为该需求提供了新方向,其核心目标是通过参数化模型逼近目标分布,KL 散度是量化逼近效果的关键工具。本文系统梳理正向与反向 KL 散度的定义、性质及适用场景:正向 KL 侧重惩罚 “漏模式”,适用于高多样性生成场景;反向 KL 侧重惩罚 “假模式”,适用于精准性优先场景。同时分析直接兼顾两类 KL 散度的矛盾与局限,指出 JS 散度为替代方案但存在实现难度大的问题,为生成式模型应用于格点场论采样提供理论基础。
本文主要参考《物理与人工智能》前沿讲座-AI与大规模数值模拟与[2510.21890] 扩散模型的基本原理 From Origins to Advances,且由AI辅助整理完成。
一、传统蒙特卡洛方法的挑战与替代方案要求
传统蒙特卡洛方法:马尔科夫链演化、Metropolis 算法、Heatbath算法、Hybrid Monte Carlo (HMC) 算法。 传统蒙卡的本质是局域更新:Heatbath 算法为严格局域更新;HMC 算法为弱非局域更新。
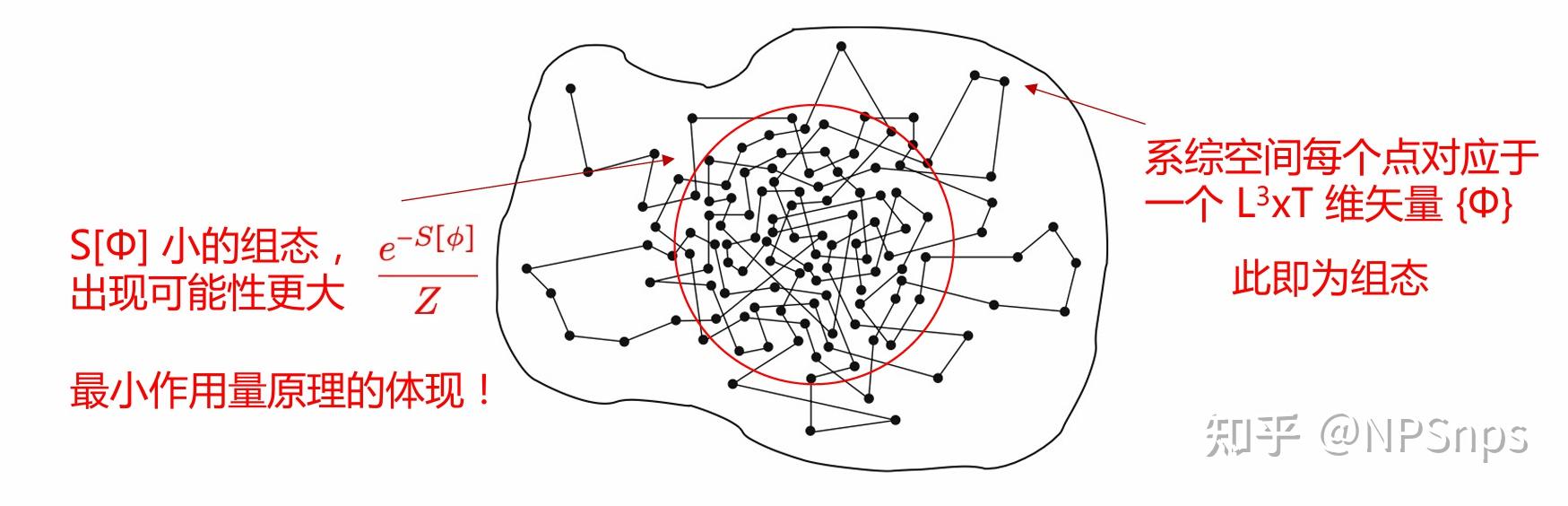
1.1 传统蒙卡的核心挑战
临界减速(Critical Slowing Down):样本高度关联性,随着格距变小,关联程度(自关联长度)急剧增长,导致采样效率大幅下降。
符号问题:有限密度条件下,化学势不为零,作用量S[Φ]非正定,给计算带来困难。
反问题:欧氏时间上的关联函数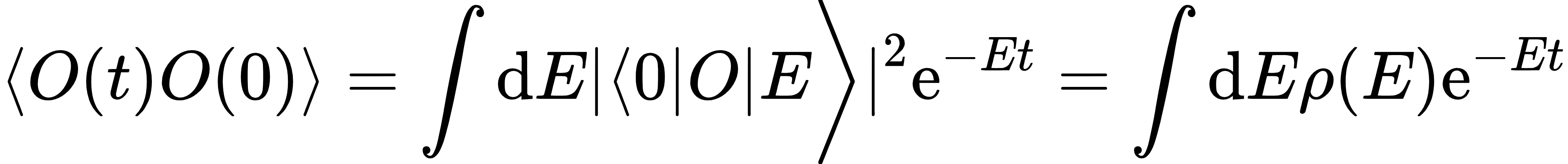 ,需从欧氏关联函数中提取谱权重 ,而欧氏与闵氏关联函数存在差异,提取过程复杂。 ,需从欧氏关联函数中提取谱权重 ,而欧氏与闵氏关联函数存在差异,提取过程复杂。
1.2 替代采样方法的关键要求
任何用于采样格点场配置的替代方法,需满足以下核心条件:
1.可统计改进(statistically improvable):样本数足够大时,能恢复真实概率分布及该分布遵守的各种对称性。
2.可扩展性:能高效扩展到最先进的格点场论研究规模,单场配置可占用TB级内存,总自由度可达1012 。
3.性能提升:在物理感兴趣的区域内改进HMC框架表现,缓解临界减速和拓扑冻结等问题。
二、生成式模型基础:KL散度与模型训练
2.1 生成式模型的核心目标
生成式模型旨在按照目标分布pdata(x)产生样本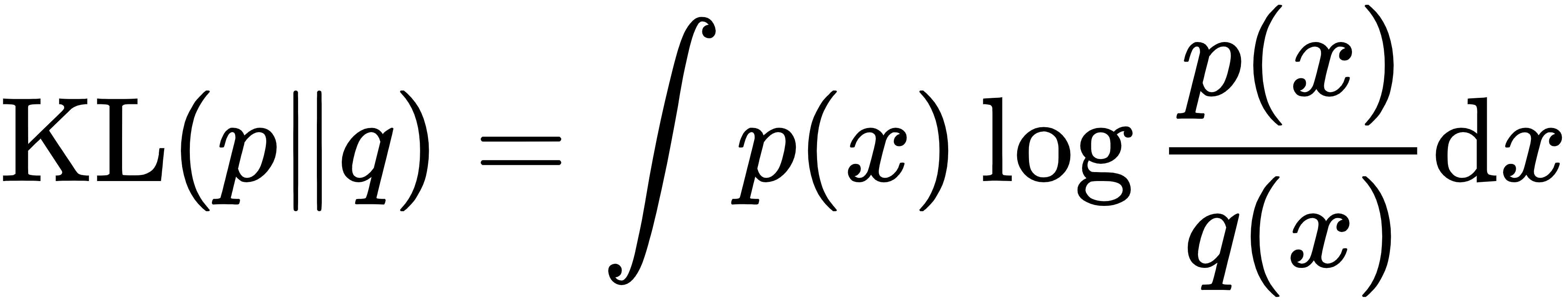 ,通过参数化模型pθ(x)逼近目标分布,量化逼近效果的核心工具是Kullback-Leibler散度(KL散度)。 ,通过参数化模型pθ(x)逼近目标分布,量化逼近效果的核心工具是Kullback-Leibler散度(KL散度)。
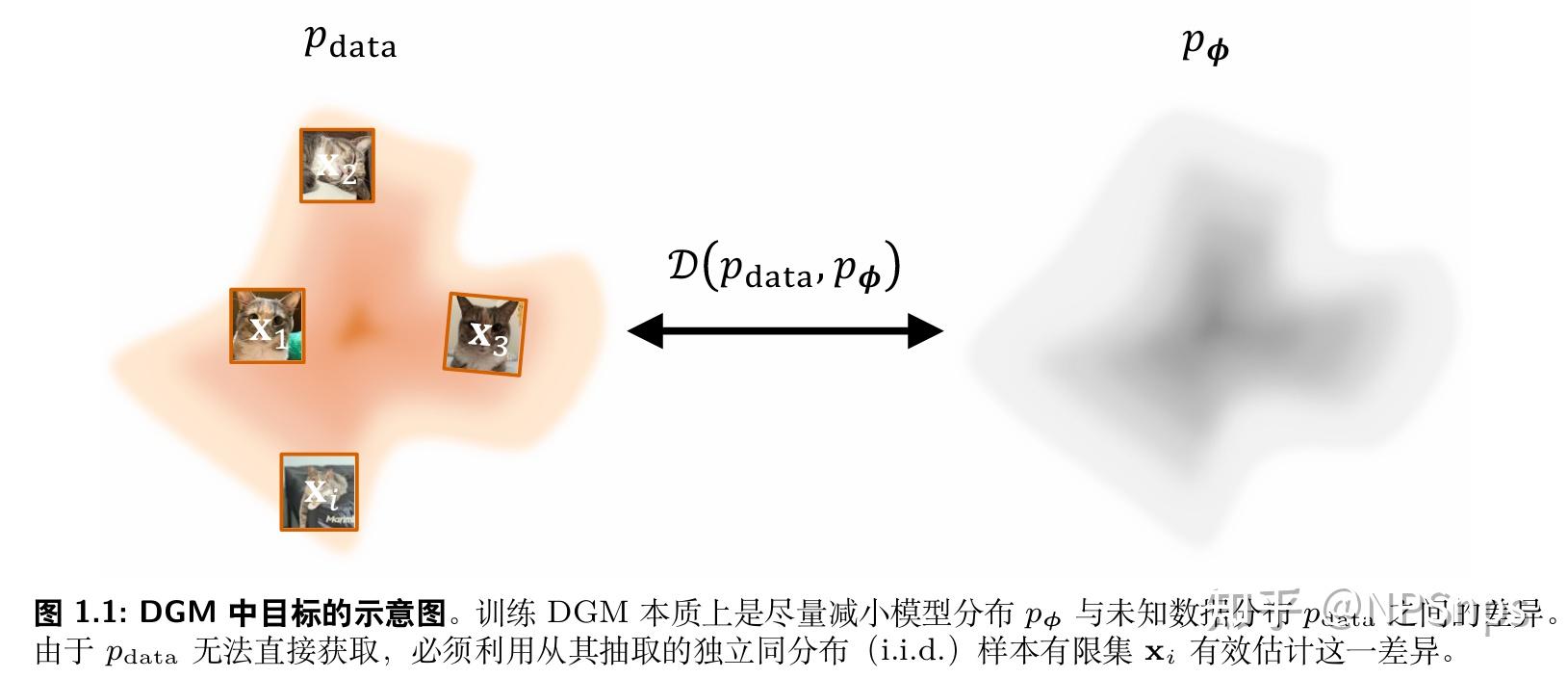
2.2 KL散度的定义与性质
定义:
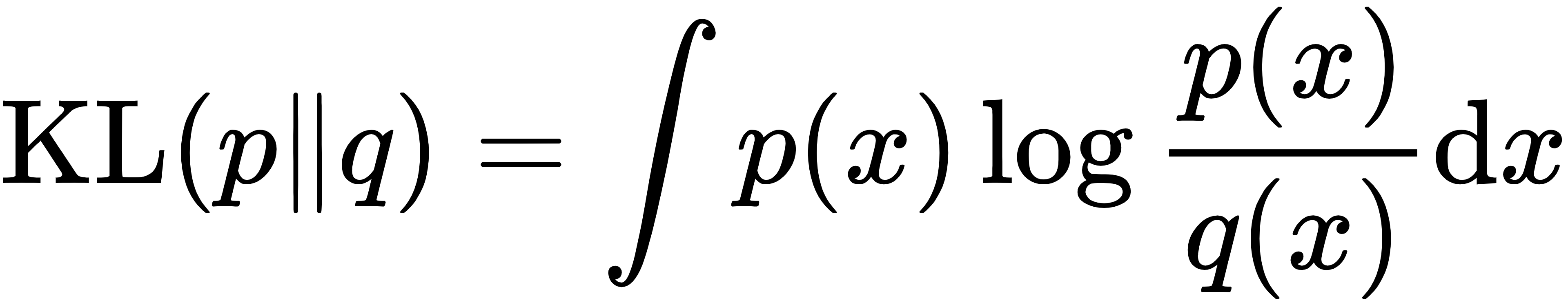
正定性:对任意正数t,满足经典不等式ln t≤ t-1(等号仅当t=1时成立)。取t=q(x)/p(x),可得:
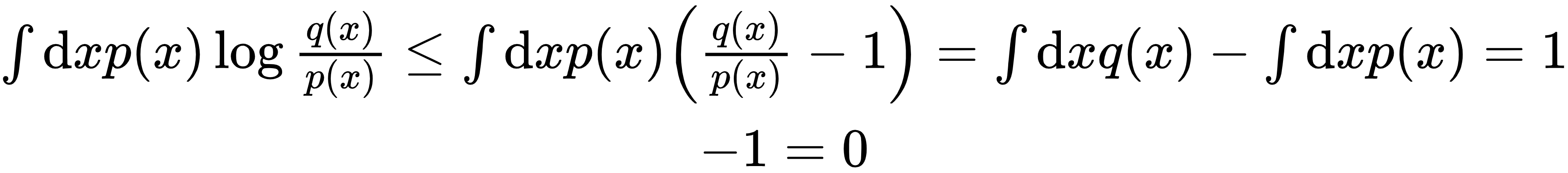
因此KL(p||q)≥0,当且仅当p(x)=q(x) 时,KL散度取极小值0。
2.3 正向KL散度与反向KL散度
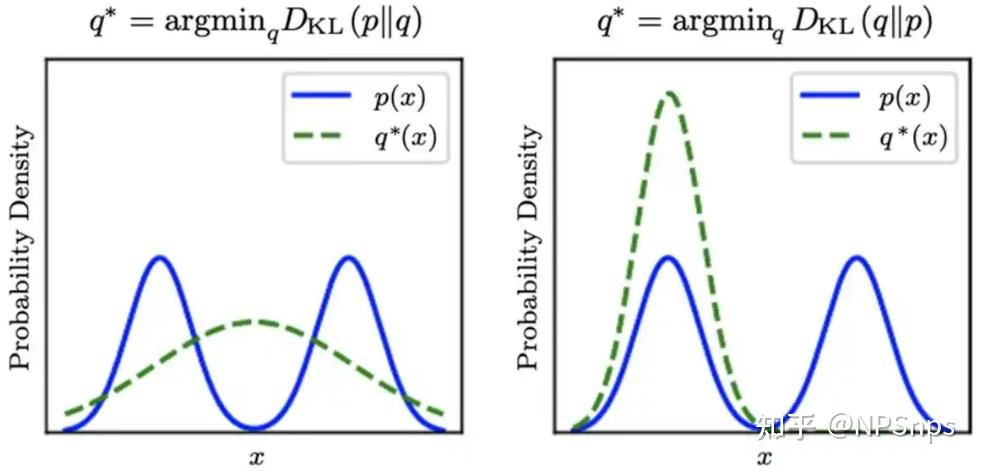
2.3.1 正向KL散度(Forward KL)
定义:
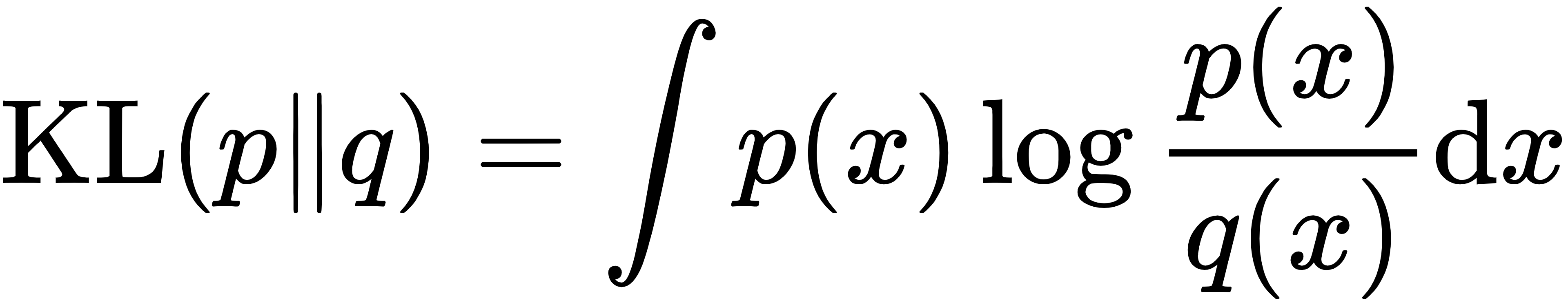
核心特点:重点惩罚“漏掉真实模式”的情况。若真实分布p(x)>0而模型分布q≈0,则log(1/q(x))→∞ ,产生无限大惩罚。
适用场景:希望模型覆盖所有真实模式、生成样本多样性高、数据分布复杂(多峰)的场景,如语言模型、扩散模型、概率密度估计,追求“全覆盖、高召回率”。
2.3.2 反向KL散度(Reverse KL)
定义:
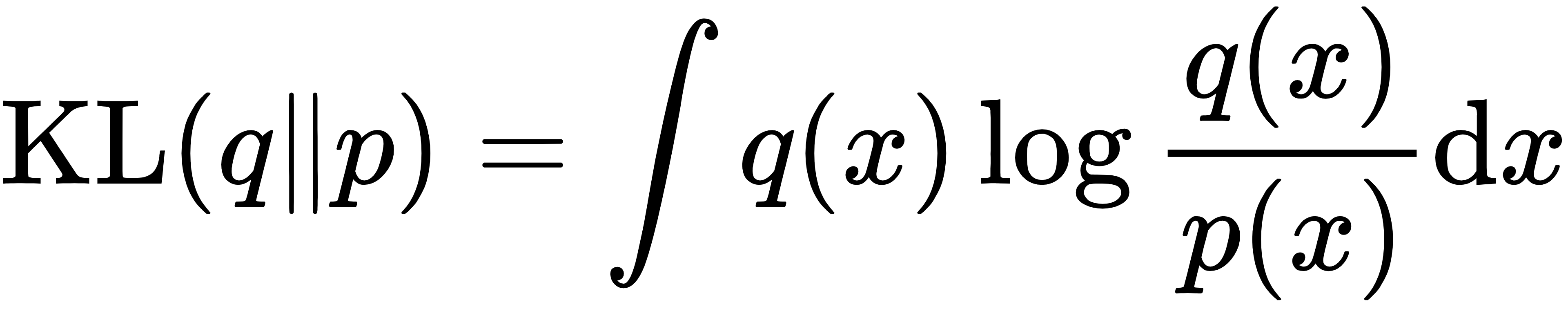
核心特点:重点惩罚“生成虚假模式”的情况。若模型分布q(x)>0而模型分布p≈0,则log(1/p(x))→∞,产生无限大惩罚。
适用场景:希望模型生成典型样本、不能容忍虚假样本、追求精准性的场景,如Normalizing flow在LQCD中的应用、某些强化学习场景、风险敏感决策,追求“典型、稳妥、集中、高精确率”。
2.4 兼顾Forward KL与Reverse KL
2.4.1 直接兼顾KL(p||q)+KL(q||p)的问题
1.惩罚方向相反:线性相加会导致模型同时承受“覆盖所有模式”和“不能多覆盖”的矛盾压力,最终陷入“中间奇怪状态”。
2.数值不稳定:过度惩罚p=0和q=0的区域,导致模型训练困难。
3.信息论无意义:最优编码长度类似于熵H(p)=E[-log p(x)] 。Forward KL对应用q去编码真实来自p的数据时额外要付出的平均编码长度,用错误的q去编码,会多付出E[-log q(x)]-E[-log p(x)]。而Reverse KL无明确物理或信息论意义,相加后无合理解释。
2.4.2 替代方案:JS散度(Jensen-Shannon散度)
定义:
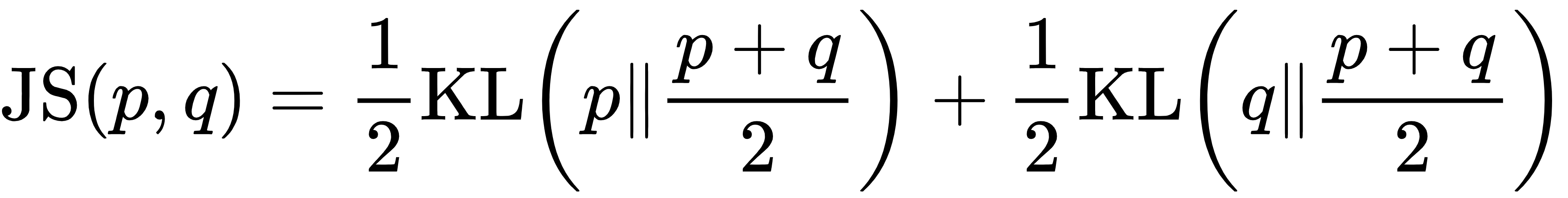
优势:非负、永不发散,避免了KL散度可能出现的发散问题。
劣势:实现难度大。KL散度可以写成
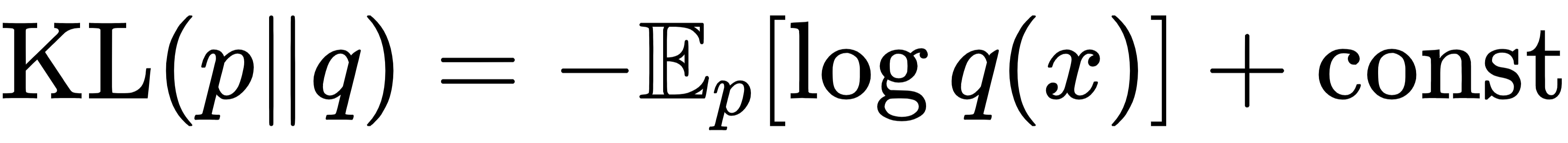
直接对模型参数求梯度,且训练非常稳定(即最大似然估计)。Reverse KL可通过恒等式
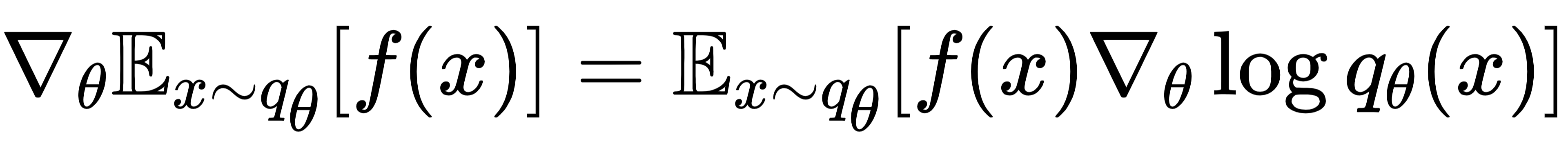
计算。而JS散度包含混合分布 ,无法直接对模型参数求梯度。
下一篇:物理学家用扩散模型(二):随机量子化+Score函数=扩散模型
文章改编转载自知乎作者:NPSnps
原文链接:https://zhuanlan.zhihu.com/p/1993075223923294383?share_code=QNB0Ftn3xvTe&utm_psn=1994706363796973069&utm_source=wechat_session&utm_medium=social&s_r=0 | 











