本帖最后由 Jack小新 于 2025-6-20 11:19 编辑
N皇后问题是经典的组合优化问题,要求在一个N×N的棋盘上放置N个皇后,使得它们互不攻击。传统上,回溯法是解决该问题的主要方法,本篇文章详细介绍了回溯法的递归与非递归实现。递归回溯法通过逐行尝试放置皇后,但效率较低;非递归回溯法则通过显式控制状态栈,提高了计算效率。通过实验对比,非递归回溯法的性能优于递归回溯法。

N皇后问题作为一个经典的组合优化问题,不仅在算法和计算机科学领域具有重要地位,还广泛应用于实际问题的求解中。N皇后问题的解决方法涵盖了回溯算法、启发式搜索、局部搜索、量子计算等多种技术,对于研究算法设计、优化策略和问题求解具有深远的影响。此外,由于其复杂性,N皇后问题也被作为算法分析和性能优化的重要基准,帮助研究人员和开发者测试和改进各种算法的效率和可行性。本系列文章将详细介绍n皇后问题及其各种解法,而在本文中,我们首先了解N皇后问题及其经典解法——回溯法的有递归和非递归两种实现方式。
1 N皇后问题
1.1 什么是N皇后问题?
在国际象棋中,皇后棋子是最强大的,可以沿着任何方向和距离移动。通常,每个玩家只有一个皇后棋子,但有一条特殊规则,允许玩家在将兵移动到对手的底线时加冕更多的皇后,皇后游戏的前提是玩家已经加冕了多个皇后(虽然这种情况在真实的比赛中可能永远不会发生,因为当玩家的国王棋子被俘获时,比赛就将结束)。
经典的 N 皇后问题最初被称为八皇后拼图,起源于国际象棋。任务是将八名皇后放置在棋盘上,而且他们中的任何两个都不互相构成威胁。换句话说,没有两个皇后可以在同一行、同一列或同一对角线。概括而言,N 皇后问题使用 NxN 的棋盘和 (其中 N>3 )个皇后。对于原始的八皇后情形,有 92个解,消除对称解,则有 12 个唯一解。使用排列组合,将 8个皇后放置在8x8棋盘上的所有可能方式有 4,426,165.368种,但是,如果通过确保不会在同一行或同一列上放置两个皇后的方式创建候选解决方案,则可能的组合数量将减少到 8!= 40320 个。
1.2 N皇后问题的不同解法
N皇后问题是一类经典的组合优化问题,其传统解法通常依赖于回溯法,通过递归搜索和剪枝策略逐步构建解空间。然而,除了回溯法之外,还有其他多种优化方法可供选择。例如,约束传播技术可以减少搜索空间,通过即时排除不满足条件的解;启发式算法如遗传算法、模拟退火和粒子群优化等则基于自然选择或随机扰动原则,探索解空间中的全局最优解,尤其适用于多峰问题。此外,局部搜索算法通过局部优化和微调路径,在较短的计算时间内找到较优解。量子计算方法也正在被探索用于解决N皇后问题,利用量子叠加和量子纠缠特性加速搜索过程。每种方法根据问题的规模、约束条件和计算资源的不同,具备不同的优势和局限。总的来说,回溯法和递归适合较小规模的问题,而遗传算法和模拟退火等启发式算法则更适合解决大规模或复杂的优化问题。选择合适的解法依赖于具体的N皇后问题规模以及所需的计算资源。
2 使用回溯法解决N皇后问题
在本文中,我们先介绍回溯法解决N皇后问题。我们来看一下回溯算法的基本思想:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
作为回溯的经典案例,N皇后问题的解决有递归和非递归两种实现方式,本文都将进行分析。
2.1 使用递归的回溯法解决
下面是用递归的回溯法求解n皇后问题的算法描述,这里用一个N*N的矩阵来存储棋盘:
1) 算法开始, 清空棋盘,当前行设为第一行,当前列设为第一列
2) 在当前行,当前列的位置上判断是否满足条件(即保证经过这一点的行,列与斜线上都没有两个皇后),若不满足,跳到第4步
3) 在当前位置上满足条件的情形:
在当前位置放一个皇后,若当前行是最后一行,记录一个解;
若当前行不是最后一行,当前行设为下一行, 当前列设为当前行的第一个待测位置;
若当前行是最后一行,当前列不是最后一列,当前列设为下一列;
若当前行是最后一行,当前列是最后一列,回溯,即清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置;
以上返回到第2步
4) 在当前位置上不满足条件的情形:
若当前列不是最后一列,当前列设为下一列,返回到第2步;
若当前列是最后一列了,回溯,即,若当前行已经是第一行了,算法退出,否则,清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置,返回到第2步。
算法的基本原理是上面这个样子,但不同的是用的数据结构不同,检查某个位置是否满足条件的方法也不同。为了提高效率,有各种优化策略,如多线程,多分配内存表示棋盘等。
在具体解决该问题时,可以将其拆分为几个小问题。首先就是在棋盘上如何判断两个皇后是否能够相互攻击,在最初接触这个问题时,首先想到的方法就是把棋盘存储为一个二维数组,然后在需要在第i行第j列放置皇后时,根据问题的描述,首先判断是在第i行是否有皇后,由于每行只有一个皇后,这个判断也可以省略,然后判断第j列是否有皇后,这个也很简单,最后需要判断在同一斜线上是否有皇后,按照该方法需要判断两次,正对角线方向和负对角线方向,总体来说也不难。但是写完之后,总感觉很笨,因为在N皇后问题中这个函数的使用次数太多了,而这样做效率较差,个人感觉很不爽。上网查看了别人的实现之后大吃一惊,大牛们都是使用一个一维数组来存储棋盘,在某个位置上是否有皇后可以相互攻击的判断也很简单。具体细节如下:
把棋盘存储为一个 N 维数组 a_N, 数组中第 i 个元素的值代表第 i 行的皇后位置,这样便可以把问题的空间规模缩为一维 O(N),在判断是否冲突时也很简单,首先每行有一个皇后,在数组中只存一元素的位置,行冲突就不存在了,其他列冲突,判断一下是否a_i与当前行要放置的列相关等。同于斜线冲突,通过观察可以发现所有在斜线上的皇后的位置都有规律即它们所在的列与行的差值 |row - i| = |col - a_i| 。这样某个位置是否可以放置皇后的问题已经解决。
下面要解决的是使用何种方法来找到所有的 N 皇后的解。上面说过该问题是回溯法的经典应用,所以可以使用回溯法来解决该问题,具体实现有两个途径,适用和非适用。适用方法较简单,大致过程如下:
void queen(int row) {
if (n == row) //如果已经找到结果,则打印结果
print_result();
else
{
for (k=0; k < N; k++) //试探第 row 行每一个列
{
if (can_place(row,k))
place(row,k); //放置皇后
queen(row+1); //继续探寻下一行
}
}
}
该方法由于在探测第i行后,如果找到一个可以放置皇后的位置j后,则会递归探测下一行,结束后则会继续探测i行j+1列,故可以找到所有的N皇后的解。完整的代码如下:
void queen(int row) {
if (n == row) //如果已经找到结果,则打印结果
print_result();
else {
for (k=0 to N) { //试探第row行每一个列
if (can_place(row,k) {
place(row,k); //放置皇后
queen(row+ 1); //继续探测下一行
}
}
}
}
2.2 使用非递归的回溯法解决n皇后问题
非递归方法的一个重要问题是何时回溯及如何回溯的问题。程序首先对N行中的每一行进行探测,寻找该行中可以放置皇后的位置,具体方法是对该行的每一列进行探测,看是否可以放置皇后,如果可以,则在该列放置一个皇后,然后继续探测下一行的皇后位置。如果已经探测完所有的列都没有找到可以放置皇后的列,此时就应该回溯,把上一行皇后的位置往后移一列,如果上一行皇后移动后也找不到位置,则继续回溯直至某一行找到皇后的位置或回溯到第一行,如果第一行皇后也无法找到可以放置皇后的位置,则说明已经找到所有的解程序终止。如果该行已经是最后一行,则探测完该行后,如果找到放置皇后的位置,则说明找到一个结果,打印出来。但是此时并不能再此处结束程序,因为我们要找的是所有N皇后问题所有的解,此时应该清除该行的皇后,从当前放置皇后列数的下一列继续探测。
完整的代码如下:
#include "iostream"
#include "cmath"
using namespace std;
#define Max 20 //定义棋盘的最大值
int a [ Max ] ;
int show(int S) //定义输出函数
{
int i,p,q;
intb [ Max ] [ Max ] ={0}; //定义并初始化b [ ] [ ] 输出数组
for(i=1;i<=S;i++) //按横列i顺序输出a [ i ] 数组坐标
{
b [ i ] [ a [ i ] ] =1;
printf("(%d,%d)\t",i,a [ i ] );
}
printf("\n");
for(p=1;p<=S;p++) //按棋盘的横列p顺序标明皇后的位置
{
for(q=1;q<=S;q++)
{
if(b [ p ] [ q ] ==1) //在第p行第q列放置一个皇后棋子
printf("●");
else
printf("○");
}
printf("\n");
}
return 0;
}
int check(int k) //定义check函数
{
int i;
for(i=1;i<k;i++) //将第k行与前面的第1~~k-1行进行判断
{
if((a [ i ] ==a [ k ] ) || (a [ i ] -a [ k ] ==k-i) || (a [ i ] -a [ k ] ==i-k)) //检查是否有多个皇后在同一条直线上
{
return0;
}
}
return 1;
}
void check_m(int num) //定义函数
{
int k=1,count=0;
printf("Thepossible configuration of N queens are:\n");
a [ k ] =1;
while(k>0)
{
if(k<=num && a [ k ] <=num)//从第k行第一列的位置开始,为后续棋子选择合适位子
{
if(check(k)==0) //第k行的a [ k ] 列不能放置皇后
{
a [ k ] ++; //继续探测当前行的下一列:a [ k ] +1
}
else
{
k++; //第K行的位置已经确定了,继续寻找第k+1行皇后的位置
a [ k ] =1; //从第一列开始查找
}
}
else
{
if(k>num) //若满足输出数组的要求则输出该数组
{
count++;
printf(" [ %d ] : ",count);
show(num); //调用输出函数show()
}
//如果k>num会执行下面两行代码,因为虽然找到了N皇后问题的一个解,但是要找的是所有解,需要回溯,从当前放置皇后的下一列继续探测
//如果a [ k ] >num也会执行下面两行代码,就是说在当前行没有找到可以放置皇后的位置,于是回溯,从上一行皇后位置的下一列继续探测
k--; //棋子位置不符合要求,则退回前一步
a [ k ] ++; //继续试探下一列位置
}
}
printf("The countis: %d \n",count);
}
int main(void)
{
clock_t start,finish;
int n;
printf("请输入皇后个数:");
scanf("%d",&n);
start = clock();
printf("\n使用非递归回溯法解决 %d 皇后问题时的运行情况\n",n);
check_m(n);
finish = clock();
printf(" 计算时间%.2fms \n", (double) (finish - start));
system("pause");
return 0;
}
该算法的巧妙之处我认为有2个:
1、以前都是用数组来描述状态,而这算法采用是的位来描述,运算速度可以大大提升,以后写程序对于描述状态的变量大家可以借鉴这个例子,会让你的程序跑得更快。
2、描述每行可放置的位置都是只用row,ld,rd这3个变量来描述,这样使得程序看起来挺简洁的。
关于n皇后问题不同算法的效果分析:
两种算法的运行结果如下(以10皇后问题为例),为了能准确分析两种算法的效率。
(1) 使用递归的回溯法时的运行情况
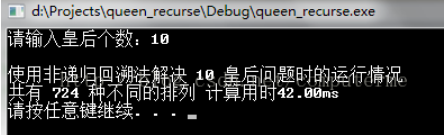
(2) 使用非递归的回溯法时的运行情况
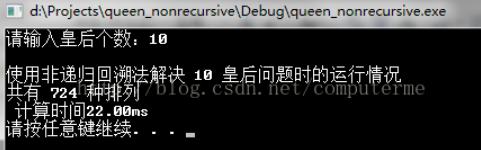
由以上的运行结果可以看到,用非递归的回溯法处理得比递归的回溯法更快。
3 小结
通过对N皇后问题的回溯法解法进行分析,我们可以看出,回溯法是解决此类组合优化问题的经典方法,特别是在较小规模的情况下。然而,递归回溯法虽然简单直观,但在效率上存在瓶颈,特别是在搜索空间较大的情况下。非递归回溯法通过显式的状态管理和栈控制,显著提升了算法的效率。
此外,如果引入位运算等其他优化策略,我们能够进一步减少不必要的计算,从而加速求解过程。我们将在下一篇介绍适合该问题的优化策略:N皇后问题(2)——回溯法的4种优化方法:对称优化、标记优化、可用优化和位运算优化。
总的来说,选择合适的解法依赖于问题规模与计算资源,而优化后的回溯法在大规模问题中表现出了更高的效率,为N皇后问题的解决提供了更加实用和高效的算法设计思路。
本文转载自CSDN博主:IT修道者
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/computerme/article/details/18080031 | 


























