本帖最后由 离子 于 2025-1-21 15:58 编辑
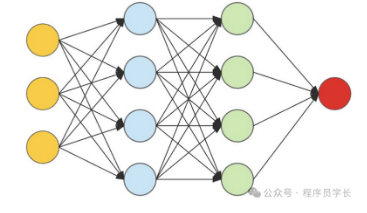
神经网络算法(Neural Network)是一种受生物神经系统启发的计算模型,广泛应用于模式识别、分类、回归等任务。
它由多个层级组成,每一层由多个神经元(节点)构成,神经元之间通过连接(边)相互作用。神经网络的目标是通过调整连接权重,使得网络能够从输入数据中学习到模式,并做出准确的预测或分类。
神经网络的基本构成
神经网络由多个层组成,包括输入层、隐藏层和输出层。每一层包含若干神经元,神经元之间通过权重连接。
输入层
输入层接收输入数据,将数据传递到网络的下一层。输入层中每个神经元代表一个输入特征。
隐藏层
隐藏层位于输入层与输出层之间,通常包含一个或多个隐藏层。每个隐藏层负责对输入数据进行特征变换。
输出层
输出层产生最终预测结果。对于回归问题,输出层通常只有一个神经元;对于分类问题,输出层的神经元数目等于类别数。

神经元的工作原理
每个神经元接收来自上一层神经元的输入信号,经过加权求和和激活函数处理后,输出结果传递到下一层神经元。神经网络通过逐层学习、逐步调整网络权重,以拟合数据中的复杂模式。

每个神经元的计算过程分为两个主要步骤
1. 输入加权求和
假设神经元的输入来自上一层神经元的输出x1,x2,......,xn ,并为每个输入分配一个权重w1,w2,......,wn
神经元的加权和计算公式为:

● 其中:wj是第j个输入的权重
● xj是第j个输入值
●bi是该神经元的偏置项
2.激活函数
加权和zi被传入激活函数f(zi)进行非线性转换,生成神经元的输出ai。

激活函数引入了非线性,使得神经网络能够学习复杂的函数映射。
常用的激活函数有:
Sigmoid

Tanh

ReLU

Softmax

import numpy as np
import matplotlib.pyplot as plt
# 1. Sigmoid 激活函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 2. Tanh 激活函数
def tanh(x):
return np.tanh(x)
# 3. ReLU 激活函数
def relu(x):
return np.maximum(0, x)
# 4. Softmax 激活函数
def softmax(x):
e_x = np.exp(x - np.max(x, axis=1, keepdims=True))
return e_x / np.sum(e_x, axis=1, keepdims=True)
x = np.linspace(-10, 10, 400)
x_softmax = np.linspace(-5, 5, 10)
x_softmax_reshaped = np.expand_dims(x_softmax, axis=0) # 添加批次维度
y_sigmoid = sigmoid(x)
y_tanh = tanh(x)
y_relu = relu(x)
softmax_output = softmax(x_softmax_reshaped)
# 绘制图像
plt.figure(figsize=(10, 8))
# Sigmoid 图像
plt.subplot(2, 2, 1)
plt.plot(x, y_sigmoid, label="Sigmoid")
plt.title("Sigmoid Activation Function")
plt.xlabel("x")
plt.ylabel("sigmoid(x)")
plt.grid(True)
plt.legend()
# Tanh 图像
plt.subplot(2, 2, 2)
plt.plot(x, y_tanh, label="Tanh", color='orange')
plt.title("Tanh Activation Function")
plt.xlabel("x")
plt.ylabel("tanh(x)")
plt.grid(True)
plt.legend()
# ReLU 图像
plt.subplot(2, 2, 3)
plt.plot(x, y_relu, label="ReLU", color='green')
plt.title("ReLU Activation Function")
plt.xlabel("x")
plt.ylabel("relu(x)")
plt.grid(True)
plt.legend()
# Softmax 图像
plt.subplot(2, 2, 4)
plt.bar(x_softmax, softmax_output[0, :], label="Softmax (3 classes)")
plt.title("Softmax Activation Function")
plt.xlabel("x")
plt.ylabel("Softmax(x)")
plt.grid(True)
plt.legend()
# 调整布局
plt.tight_layout()
plt.show()

神经网络的训练过程
神经网络的训练过程是一个迭代优化的过程,旨在通过调整网络中的参数(如权重和偏置)来使得模型能够更好地拟合数据,进而提高模型的预测能力。训练过程通常包括数据的前向传播、损失计算、反向传播、梯度更新等多个步骤。
1. 初始化参数
在开始训练之前,神经网络中的所有参数(权重和偏置)需要被初始化。初始化方法直接影响神经网络训练的效率和效果。常见的初始化方法包括:
随机初始化
使用小的随机值初始化权重,通常可以用高斯分布或者均匀分布生成权重值
Xavier初始化
根据输入和输出节点的数量调整权重初始化的范围,使得每一层的输出方差保持相同,适用于Sigmoid和Tanh激活函数。

其中nin和nout分别是输入层和输出层的神经元数。
He初始化
主要用于 ReLU 激活函数的网络,权重初始化为均值为 0,方差为2/nin的高斯分布。偏置通常会初始化为零或者小的常数值。
2.前向传播
前向传播是神经网络训练的第一步,它的目的是计算出每一层的输出并最终获得网络的预测结果。
输入层到隐藏层
对于第l层的第i个神经元,其加权和zi(l)为:

其中,aj(l-1)是第l-1层的第j个神经元的输出,wij(l)是连接第l-1层第j个神经元与第l层第i个神经元的权重,bi(l)是偏置。
激活函数
得到加权和zi(l)后,然后通过激活函数(如 ReLU、Sigmoid、Tanh 等)得到神经元的输出ai(l)
其中,  是激活函数。 是激活函数。
最终输出
经过所有的层,最终得到输出层的激活值y^,这是神经网络的预测结果。

3. 损失计算
损失函数用于衡量神经网络预测结果与实际标签之间的差距。根据任务类型的不同,选择不同的损失函数。
均方误差(MSE)
用于回归问题,表示预测值与真实值之间的平均平方差。

其中,yi是实际值,yi^是预测值,N是样本数。
交叉熵损失(Cross-Entropy Loss)
其中, yi是实际标签的概率分布,yi^是预测标签的概率分布。
损失函数是神经网络优化的目标,我们要通过梯度下降法来最小化这个损失。
4. 反向传播
反向传播是神经网络训练过程中的核心,它通过链式法则计算损失函数相对于每个参数(权重和偏置)的梯度。

这些梯度随后用于更新参数,以减少损失函数值。
具体步骤如下:
计算输出层的梯度
首先,计算输出层的损失函数对输出激活值a(L)的梯度。对于交叉熵损失函数,输出层的梯度为:

然后,将其与激活函数的导数 相乘,得到对加权和z(L)的梯度: 相乘,得到对加权和z(L)的梯度:

反向传播误差
然后,误差从输出层向前传播,逐层计算每一层的误差。
其中, 是第l层的误差,W(l+1)是第l层到第l+1层的权重矩阵, 是第l层的误差,W(l+1)是第l层到第l+1层的权重矩阵, 是激活函数对加权输入z(l)的导数。 是激活函数对加权输入z(l)的导数。
计算权重和偏置的梯度
对于每一层,我们计算损失函数相对于权重和偏置的梯度:
对权重的梯度:
对偏置的梯度:
5.更新权重与偏置

根据计算出的梯度,使用以下公式更新权重和偏置:

其中:
 是学习率,控制每次参数更新的步长。 是学习率,控制每次参数更新的步长。
 和 和  分别是权重和偏置的梯度。 分别是权重和偏置的梯度。
梯度下降的目标是通过不断更新参数,使损失函数逐渐减小,最终收敛到最优解。
6. 迭代训练
在神经网络训练过程中,前向传播、损失计算、反向传播和参数更新的过程会重复多次。
每次完整的前向传播和反向传播过程称为一个epoch。
通常,训练会进行多个epoch,直到损失收敛或达到预定的最大 epoch 次数。
7. 模型评估
训练完成后,神经网络的性能需要通过测试数据进行评估。
通过计算模型在测试集上的损失和准确率等指标,判断训练效果如何。
如果模型效果不好,可能需要调整网络结构、学习率、批量大小等超参数,重新进行训练。
案例分享
以下是一个使用神经网络进行手写数字识别的完整示例代码。
import tensorflow as tf
from tensorflow.keras import layers, models
import matplotlib.pyplot as plt
import numpy as np
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
model = models.Sequential([
layers.Flatten(input_shape=(28, 28)), # 将输入的 28x28 图片展平成一维向量
layers.Dense(128, activation='relu'), # 隐藏层,128个神经元,使用 ReLU 激活函数
layers.Dropout(0.2), # Dropout 层,避免过拟合,随机丢弃20%的神经元
layers.Dense(10, activation='softmax') # 输出层,10个神经元(代表0-9的数字),使用 Softmax 激活函数
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy', # 对于多分类问题,使用交叉熵损失函数
metrics=['accuracy'])
history = model.fit(x_train, y_train, epochs=5, validation_data=(x_test, y_test))
test_loss, test_acc = model.evaluate(x_test, y_test)
print(f"Test accuracy: {test_acc}")
plt.figure(figsize=(8, 4))
plt.plot(history.history['loss'], label='Training loss')
plt.plot(history.history['val_loss'], label='Validation loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

本文转载自微信公众号:程序员学长
|












