本帖最后由 graphite 于 2025-1-21 15:45 编辑
拉格朗日乘子法是最优化问题中的一个强大工具,尤其适用于求解带约束的最优化问题。其核心思想是通过引入辅助变量(拉格朗日乘子)将原始问题转化为一个无约束的最优化问题,从而求得约束条件下的最优解。该方法不仅在数学分析中有着广泛的应用,也在物理学、工程学、经济学等多个领域中发挥着重要作用。
在现实生活中,很多优化问题不仅仅涉及到要最大化或最小化某个目标函数,还需要满足一定的约束条件。比如,工程设计中要在满足安全要求的前提下最大化材料的使用效率;经济学中,企业可能在成本最小化的同时需要遵守生产能力等约束。如何在这些约束条件下找到最优解,成为了科学和工程领域中的一个重要课题。拉格朗日乘子法作为一种求解约束最优化问题的方法,已经广泛应用于物理学、工程学、经济学等学科。
拉格朗日乘子法的独特之处在于它通过引入辅助变量,将约束条件融入到目标函数中,转化为一个无约束的最优化问题,从而简化了求解过程。尽管拉格朗日乘子法的数学框架相对简洁,但其内涵却极为丰富,涉及到微积分、线性代数以及函数优化等多个数学分支。通过对拉格朗日乘子法的深入理解,我们能够更好地应对各种复杂的最优化问题。
1. 拉格朗日乘子法的基本原理
1.1 最优化问题的定义
最优化问题是指在一组变量中,寻找一个最优解,使得某个目标函数达到最大值或最小值,同时满足一些约束条件。一个典型的最优化问题可以表示为:

其中,f(x1,x2,......,xn)是目标函数,gi(x1,x2,......,xn)是约束条件,m 是约束的数量。
传统的最优化方法,如直接对目标函数进行求导和求解,通常无法有效处理约束条件。拉格朗日乘子法的作用就是通过构造一个新的函数,将约束条件纳入其中,从而把带约束的最优化问题转化为一个无约束的问题。
1.2 拉格朗日乘子的引入
拉格朗日乘子法通过引入拉格朗日乘子(  )来处理约束条件。拉格朗日函数的形式为: )来处理约束条件。拉格朗日函数的形式为:
其中, 是拉格朗日乘子,表示每个约束条件的重要性。在此基础上,我们需要对拉格朗日函数 L 对所有变量进行求导,并令其导数为零,从而求得最优解。 是拉格朗日乘子,表示每个约束条件的重要性。在此基础上,我们需要对拉格朗日函数 L 对所有变量进行求导,并令其导数为零,从而求得最优解。
1.3 求解过程
1.3.1 一阶必要条件
通过对拉格朗日函数分别对x1,x2,......,xn和 求偏导数,并令其等于零,可以得到一组方程: 求偏导数,并令其等于零,可以得到一组方程:

这些方程构成了一个包含 n+m 个未知数的方程组。解这个方程组可以得到最优解。需要注意的是,这些条件只是局部最优解的必要条件,实际上可能存在多个解,需要进一步验证哪一个解是全局最优解。
1.3.2 约束的类型
拉格朗日乘子法主要适用于等式约束的情形。当约束为不等式时,通常需要使用其他方法,如卡尔什-库恩-塔克(KKT)条件等。
2. 拉格朗日乘子法的几何解释
2.1 几何意义:约束条件的切平面
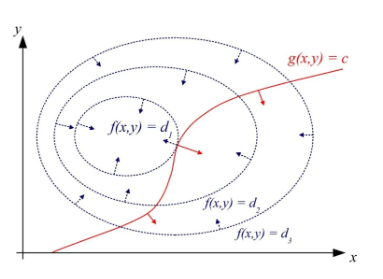
为了更直观地理解拉格朗日乘子法,我们可以借助几何视角。假设目标函数f(x1,x2,......,xn)和约束函数gi(x1,x2,......,xn)都是连续可微的,且约束条件gi=0定义了一个约束面。
在优化过程中,我们寻求的是目标函数在约束面上的最优值。从几何上看,拉格朗日乘子法的本质是找到一个点,使得目标函数的梯度和约束条件的梯度在该点上是线性相关的。这意味着,目标函数在该点的变化方向与约束条件的切平面平行。
2.2 梯度的线性相关性
在最优点上,目标函数的梯度和约束条件的梯度之间存在某种比例关系。具体来说,拉格朗日乘子 表示约束条件gi(x)=0对目标函数优化的“影響程度”——即当约束条件发生微小变化时,最优解会如何变化。 表示约束条件gi(x)=0对目标函数优化的“影響程度”——即当约束条件发生微小变化时,最优解会如何变化。
这种梯度的线性相关性可以通过下面的关系来表达:

这一几何解释为拉格朗日乘子法提供了深刻的直觉,使得我们能够更容易理解为何该方法能够有效地求解约束最优化问题。
3. 拉格朗日乘子法的应用
3.1 物理学中的应用
拉格朗日乘子法在物理学中的应用非常广泛,特别是在经典力学中的变分问题。经典力学中的拉格朗日方程本质上就是拉格朗日乘子法的一个特例。例如,在分析带有约束的物体运动时,我们可以通过引入拉格朗日乘子来处理约束条件,解决最优化问题。
3.2 经济学中的应用
在经济学中,拉格朗日乘子法常用于求解带约束的最优化问题。举例来说,企业可能希望在成本最小化的前提下最大化生产效率,或者消费者希望在预算约束下最大化效用。拉格朗日乘子法可以帮助找到这些经济问题的最优解。
3.3 工程学中的应用
在工程学中,拉格朗日乘子法也被广泛应用于各种设计优化问题中。例如,结构设计中要求最小化材料使用量或最大化稳定性时,常常需要考虑约束条件如材料的强度、尺寸等。
4. 拉格朗日乘子法的局限性与发展
4.1 局限性
拉格朗日乘子法有其固有的局限性。首先,该方法假设目标函数和约束条件是连续可微的,这限制了其适用范围。其次,当约束条件为不等式时,拉格朗日乘子法就不再适用,需要采用其他方法,如卡尔什-库恩-塔克条件。此外,拉格朗日乘子法只能找到局部最优解,在非凸问题中,可能无法保证得到全局最优解。
4.2 未来展望
随着计算技术的发展,拉格朗日乘子法在复杂优化问题中的应用愈发广泛。近年来,拉格朗日乘子法的变种和扩展,特别是在处理不等式约束和非线性约束方面,已成为研究的热点。例如,现代最优化理论中,拉格朗日乘子法与其他数值优化方法(如内点法)相结合,已被广泛应用于高维、大规模优化问题。
本文转载自微信公众号:科学与技术研发中心 | 


























