量子力学是用于描述微观世界的理论,常被视为近代物理学的开端。近年来,量子力学的理论被应用在许多领域,包括被誉为"下一代计算工具"的量子计算机(Quantum computer)。相较于传统计算机,量子计算机可在短时间内处理海量信息。量子计算机技术主要涉及三个核心概念——"量子叠加(Quantum superposition)"、"量子纠缠(Quantum entanglement)"与"量子干涉(Quantum interference)"。本文将针对"量子叠加"展开深入解析。
1. 量子叠加的基础问题
1.1 经典物理与量子世界的本质区别
自牛顿建立起描述宏观世界的经典力学体系以来,确定性一直被视为物理世界的基本属性:无论是行星的运行轨道,还是钟摆的周期摆动,只要初始条件明确,便可精确预言系统在任意未来时刻的状态。然而,当人类的观察尺度深入至原子乃至更小的基本粒子层面时,建立在连续性与因果律基础上的经典物理范式遭遇了前所未有的挑战。微观粒子的行为展现出非连续性与概率性特征,无法用经典轨迹描述,且其状态不再具有唯一且确定的取值,而是在未被测量前以某种“潜在可能”的方式共存于多个状态之中。
量子力学的核心突破,正是重新定义“状态”这一概念。
与经典物理中物体的状态可由位置与动量等实数变量完整描述不同,量子系统的状态需由一类抽象的数学对象——波函数——加以刻画,使其不仅包含了系统所有可能状态的信息,而且以概率幅的形式编码着系统在不同状态间的“倾向性”。波函数的本质并非对客观现实的模糊描述,而是体现了一种“非排他性的同时存在”——即所谓的量子叠加(Quantum Superposition)。
由此,电子既非处于某一确定轨道上运行的微型行星,也非以随机漫步方式漂浮的“概率云”,而是在测量发生之前,真实地处于所有可能路径的叠加态中。
 图:两个物体处于量子叠加态的示意图(ShutterStock) 图:两个物体处于量子叠加态的示意图(ShutterStock)
然而,这样的重新定义又引出了新的问题:当一个量子系统被测量时,其波函数将瞬间“坍缩”至某一具体本征态,表现出一种从多种可能中选取唯一结果的非连续跃变——这一过程本身并不受经典因果律的支配,且无法通过任何已知机制加以预言;换言之,即便一个实验在完全相同的初始条件下重复进行,其测量结果亦可能因概率而呈现出不同的统计分布。
1.2 量子叠加态的定义与量子比特
如果说经典比特是“非黑即白”的开关,那么量子比特则是穿梭在黑与白之间的一种更为丰富的存在方式。所谓量子叠加,指的是微观粒子在未被观测前,并不“选择”一个确定的状态存在,而是以一种数学上可表述为多个可能状态“同时存在”的方式运行。
例如,在量子计算中,最基本的信息单元不是只能取0或1的经典比特,而是能够同时处于“0态”和“1态”之间某种中间状态的量子比特(qubit)。这种状态的数学形式通常写作:|ψ⟩=α|0⟩+β|1⟩,其中|0⟩和|1⟩是量子比特的两个基本状态,而α和β则是描述其所处状态的复数系数。
这两个系数本身并不具有直接的物理意义,但它们的模长平方(即|α|2与|β|2)分别代表了当我们对该量子比特进行测量时,它坍缩为“0态”或“1态”的概率。由于概率的总和必须为1,因此有归一化条件:|α|2+|β|2=1。
需要特别指出的是,所谓“叠加”并非像将两个颜色混合那样的模糊状态,也不同于一个经典骰子在空中翻滚、我们只是暂时不知道其点数的“不确定性”;量子叠加是真正地、客观地允许粒子在未被测量前处于两种状态的线性组合之中,它符合一套非常严谨的数学规则。
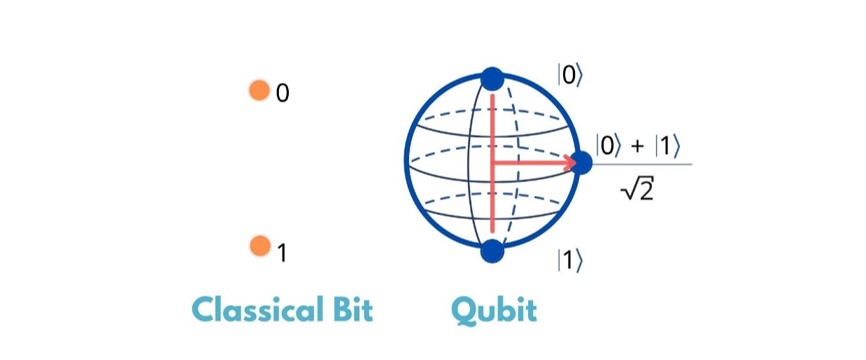
图:经典粒子状态与量子比特叠加态 by Adrian Hsu
叠加态之间存在着所谓的“干涉效应”——两种状态的概率幅可以彼此相加,也可以相互抵消。不同的叠加方式将导致完全不同的测量结果,哪怕两者都“包含”0与1。这一点非常重要,正是因为有了叠加与干涉,量子系统才展现出远超经典信息处理的潜力,使得量子计算能够在某些问题上实现指数级别的加速。
1.3 波函数与叠加态的数学描述
要理解量子叠加的数学本质,首先必须认识到:在量子力学的理论框架中,系统的状态不再是一个关于位置、速度等物理量的简单集合,而是由一个定义在抽象希尔伯特空间中的向量来刻画,其具体体现形式就是我们所熟知的波函数ψ(x,t)。波函数本质上是一种概率幅的分布,它并不直接描述粒子“实际存在”在某个位置,而是给出了我们在某一时间t测量粒子出现在空间中位置x的概率大小。这一概率由波函数的模平方|ψ(x,t)|2给出。
对于一个处于叠加态的量子系统,波函数可以被表达为多个“本征态”的线性组合。所谓本征态,是指当系统受到某个物理量(如能量、动量或位置)相关的算符作用时,其形式不发生改变,只被乘上一个常数因子的状态。以位置算符为例,一个粒子处于某个确定位置的状态就是该算符的本征态。我们可以将一个一般状态下的粒子波函数表示为多个位置本征态的线性叠加,即:

其中ψ1(x)和ψ2(x)分别代表粒子处于位置x1和x2时的波函数部分,整个系统的波函数则是这两者的叠加。然而这并不意味着我们对粒子究竟处于哪一位置“尚不清楚”,而是意味着在物理实在层面上,它同时具有出现在两个位置的能力——只是在测量发生之前,这种能力仍保持共存的状态。
这一看似悖于常识的事实,已在大量实验中得到印证,其中最具代表性的莫过于双缝实验。
1.4 实验验证:从双缝实验到薛定谔猫
量子叠加的概念如果仅停留在数学符号的层面,或可被理解为某种便于计算的抽象构造;然而,自20世纪初以来,一系列严谨设计的实验表明,这种“一个粒子可以同时处于多个状态”的设想,并非仅仅是理论模型的产物,而是物理世界中客观可证的现实特征。其中最具代表性的,是双缝实验所揭示的干涉现象,它以几乎挑衅直觉的方式,直面量子叠加的真实存在。
设想一束电子逐个地发射,穿过一道布有两条狭缝的屏障,最终落在后方的探测屏上。如果我们尝试用经典物理的思维方式理解这一过程——电子作为粒子应当选择穿过某一条缝隙并落在某个具体位置上——那么我们预期在探测屏上观察到的是两个高峰,分别对应穿过左缝或右缝的概率。
然而实验所呈现的却是:电子似乎不仅穿过了左缝,也穿过了右缝,更关键的是,它们之间还相互“干涉”,在某些位置增强,在另一些位置相互抵消,最终构成了明暗相间的条纹结构。更令人困惑的是,即便将电子逐个发射,每次只有一个电子进入实验装置,干涉图样依然逐渐形成,这表明干涉并非来自粒子间的相互作用,而是来自单个粒子“自身状态的叠加”。
为了进一步检验这一现象的本质,物理学家在缝口附近安置探测器,试图“看清楚”电子到底穿过了哪一条缝。但奇异的是,一旦引入观测装置,干涉图样立即消失,转而呈现出经典概率分布的两峰结构。这一现象并不意味着电子改变了路径,而是表明:测量行为本身改变了系统状态,使原本保持叠加的波函数“坍缩”至某一具体结果。
进一步地,著名物理学家薛定谔提出了一个看似荒谬的思想实验——薛定谔的猫,以质疑将叠加态概念推广至宏观世界的合理性。他设想一个密闭盒子,盒中放置一只猫、一瓶剧毒气体和一个连接放射性原子的触发装置:若原子发生衰变,则触发机制释放毒气,猫便死亡;若原子未衰变,猫则安然无恙。根据量子力学的规则,在尚未打开盒子之前,原子的状态应为“衰变”与“未衰变”的叠加,那么与其相连的装置状态也应保持“启动”与“未启动”的叠加,进一步推导则意味着:猫也应处于“生”与“死”两种状态的叠加中。
尽管薛定谔本人并不打算主张猫真的处于这种奇异状态,而是试图借此揭示量子理论在描述宏观世界时可能面临的悖论,但讽刺的是,现代实验技术的进展——尤其是对大分子、超导系统与宏观量子相干态的操控能力——正在逐步缩小微观与宏观之间那道曾被认为是不可逾越的鸿沟。
 图:薛定谔的猫 图:薛定谔的猫
因此,无论是在实际实验中观察到的干涉现象,还是在思想实验中逼近理论极限的逻辑推演,都不容否认地指向一个结论:量子叠加并非某种人类认知的缺陷,也非实验手段的局限,而是构成微观世界基本结构的实在原则。
2. 相干性与测量的基础问题
2.1 相干性:叠加态维持的关键条件
量子叠加的存在虽然在双缝实验与诸多干涉实验中得到了充分验证,但真正构成其有效性基础的,并不是“叠加”本身,而是系统维持“叠加结构”的能力,即所谓的相干性(coherence)。换言之,量子叠加并非孤立地存在于数学公式中,而需要一种对干扰高度敏感、极易被破坏的动态平衡结构作为支撑;正是这种结构决定了一个量子系统能否真正体现出与经典系统本质不同的行为特征。
从数学角度而言,所谓相干性,可以理解为系统波函数中不同状态之间存在确定的相位关系。以最简单的两态叠加为例,假设一个量子比特处于|ψ⟩=α|0⟩+β|1⟩的状态,其中α与β不仅大小相关,更重要的是它们之间的相位差(phase difference)决定了系统在干涉实验中的行为表现。当外界环境未对系统造成扰动时,这种相位结构得以稳定维持,系统即可呈现如双缝干涉图样、量子算法叠加操作等精妙现象。
然而,一旦系统开始与环境发生不可忽略的相互作用,哪怕仅仅是极为微弱的信息泄露,其叠加结构中的相位关系便会迅速失去控制,导致原本可以发生干涉的分量变得不可区分。此时,尽管波函数在形式上仍然可以写作线性组合,但由于各个分量之间的量子相干性已丧失,系统便不再具备典型的量子行为,而趋于经典概率混合的表现形式。用密度矩阵的语言来描述这一过程最为清晰:若系统初始处于纯态ρ=|ψ⟩⟨ψ|,其密度矩阵将包含非零的“非对角项”(off-diagonal elements);而一旦环境干扰引入退相干效应,这些非对角项便迅速衰减至零,系统的密度矩阵变为对角形式,量子叠加遂不复存在。
因此,相干性不仅是量子叠加态得以维持的先决条件,更是量子信息得以保持与操控的核心资源。在量子计算与量子通信等前沿技术中,大部分情况下整个系统的设计原则皆围绕如何延长相干时间、减缓相干性的损耗展开。正如在经典信息论中我们关心信道容量与误码率,在量子体系中,相干性就是维系计算正确性的根本“能量”所在。
2.2 退相干现象:环境干扰与量子信息丢失
如果说相干性是支撑量子叠加态物理实在性的核心结构,那么退相干(decoherence)则是这一结构最根本的威胁。所谓退相干,指的是量子系统在与外部环境发生不可避免的相互作用过程中,其原本清晰的相位关系逐渐丧失,最终表现为系统由一个可干涉的量子态转变为一个仅能以经典概率描述的混合态。这一过程既非由外力强行扰动导致的破坏性变化,也不是测量行为直接引起的波函数坍缩,而是一种由信息“泄露”所触发的不可逆演化过程,它以极其微妙却又不可挽回的方式侵蚀着量子性本身。
在理想情况下,一个封闭的量子系统的演化由薛定谔方程所决定,其波函数随时间变化服从严格的线性和可逆性。然而在现实中,任何物理系统都不可避免地与环境耦合,我们无法也不可能完整追踪整个“系统 + 环境”的总波函数。因此,我们常用密度矩阵ρ(t)来描述系统的状态演化。当系统与环境存在耦合时,系统态不再是纯态,而是混态,其演化通常服从如下形式的主方程:

其中HS是系统自身的哈密顿量,而D[ρ]是所谓的“散度项”或“耗散超算符”,它以非单位演化的方式体现了环境对系统状态的干扰。在ρ的表示中,最能体现量子相干性的就是其非对角项(off-diagonal elements),也是系统中各叠加分量之间相位关系的反映。一旦系统受到环境的扰动,这些非对角项便呈指数衰减,直至近乎为零,意味着原本能够发生干涉的状态被环境“标记”为可区分,从而失去了叠加能力。

图:环境干扰下的量子信息丢失机制
图中展示了一个原本处于纯态 ∣ψ(t)⟩ 的量子系统在与环境发生耦合后,其密度矩阵从包含非对角项的纯态 ρ(t)=∣ψ(t)⟩⟨ψ(t)∣ 演化为对角混合态的过程。外界干扰以波动箭头形式表示,象征系统与环境之间的信息交换导致相干性的逐步丧失。非对角元素的衰减反映了量子相位关系的破坏,进而造成干涉能力的消失,使系统行为趋近于经典概率分布。这一过程是退相干的核心机制,标志着从量子叠加向经典行为的过渡。
退相干的本质,在于信息的不对称流动:当系统与环境发生相互作用时,一部分原本只存在于系统内部的相位信息开始在环境中留下“痕迹”。哪怕我们未主动观测,环境本身也可以被视作一个无形的测量者,它不断地从系统中“读取”状态信息,使得系统不再是一个封闭演化的波函数,而是成为一个失去内在一致性的开放系统。从信息论角度看,退相干可视为系统信息熵增加的过程,是量子信息以不可控方式向环境泄露、而非局域保持的体现。
退相干的实际影响极其深远。对于量子计算而言,退相干意味着量子比特间的叠加与纠缠关系被破坏,计算结果失真,量子算法的优势丧失;而在量子通信中,退相干则会导致信息传输过程中出现噪声与错误,使得量子密钥分发的安全性受到威胁。因此,构建低退相干率的量子系统、延长量子态的相干时间,成为量子技术发展的核心挑战之一。
此外,退相干过程尽管会使系统趋近于经典行为,却并不等价于“测量”本身,也不会自动导致波函数坍缩。它只是在统计意义上抹除不同状态之间的干涉能力,使得系统行为在宏观上更接近经典物理的预测,从而在不引入额外诠释的前提下,为“为何宏观世界表现为经典”的问题提供了一个机制性的解释,也构成了当代“环境诱导经典性”(environment-induced superselection, 或称einselection)理论的基础。
2.3 量子测量问题:叠加态的坍缩与观测悖论
尽管量子力学在预测微观世界中的实验结果方面取得了惊人的成功,其数学结构亦极为精巧优雅,但当我们试图探讨测量行为的本质时,却不得不面对一个长期悬而未决的难题:为何在测量发生时,系统会从多个叠加态中“选择”出一个具体结果?这一问题,即所谓的量子测量问题(quantum measurement problem),构成了量子理论体系中最根本、也最富争议的哲学难题之一。在标准的哥本哈根解释中,量子系统的演化具有双重性:在没有测量时,其状态由薛定谔方程控制,呈现出线性、可逆的连续演化:

而一旦测量发生,系统便瞬间从原先的叠加态:

“坍缩”到其中一个本征态|ak⟩,对应的概率为|αk|2,坍缩过程是非线性的、不可逆的、瞬时发生的,且无法由薛定谔方程导出。更为复杂的是,测量行为本身并不必然需要人类意识的介入。以现代实验物理中的自动探测装置为例,系统与仪器的耦合便足以导致结果的坍缩。那么,若这一过程仍被视为“测量”,我们就不得不追问:到底哪一个环节——系统与仪器的耦合?仪器状态的宏观放大?还是人类意识的最终读取?——才是波函数坍缩发生的决定性界面?——这正是著名的“冯·诺依曼链(von Neumann chain)”所揭示的问题:如果测量设备本身也可被视为一个量子系统,那么系统—设备—观测者之间应组成一个更大的叠加体系,坍缩又应何以发生?
面对这些难题,部分现代理论尝试将测量行为重新解读为系统与环境之间的“信息分离”过程。例如,前文所述的退相干机制已表明,一旦系统与环境发生不可逆的信息交换,系统叠加态中的不同分量便会在环境中留下可区分的“痕迹”,从而失去相干性。尽管退相干本身不足以解释为何测量结果“落入”某一具体本征态,但它确实为经典状态如何在宏观层面涌现提供了机制解释。换言之,在环境作用下,系统虽然在理论上仍处于全体可能性的叠加之中,但由于这些可能性已不可观测地分散至环境,观测者所能获取的仅是一种有效“坍缩”的投影。
另一些理论,如“多世界解释”(Many-Worlds Interpretation),则更为激进地否认波函数坍缩的现实性,主张测量实际上并未消除叠加,而是导致观测者与被测系统一同进入多个平行分支之中,每一个分支对应一种可能结果的实现。在这种框架下,坍缩只是一种主观的错觉,而宇宙总体状态始终保持完整的叠加结构。
然而,无论采取何种诠释,量子测量问题都清楚地揭示了量子理论的一个关键之处:它既是一套用于描述自然规律的数学工具,也不可避免地涉及我们如何定义“现实”与“信息”的边界。正如物理学家约翰·贝尔所指出的,“测量”不应被视为一个基础的概念,而应是理论自身演化与系统划分结构中的一个衍生现象;否则,我们只能不断将“谁在测量谁”的问题无限向外推移,直至无法收敛。
3. 结语:量子叠加的现实应用与未来路径
量子叠加在许多领域已经有了广泛应用。首先,在量子计算领域,叠加态为信息存储与处理提供了指数级的状态空间扩展,使得量子比特能够在一次操作中并行探索多个路径,从而打破传统计算在特定问题上的复杂度瓶颈。例如Shor算法利用叠加与量子傅里叶变换,实现了对大整数因式分解的指数级加速,为现代加密体系提出了根本性挑战,也成为量子计算机可行性的重要里程碑。
其次,在量子通信中,叠加态与纠缠态共同构成了无条件安全通信的物理基础。量子密钥分发协议(如BB84)正是利用叠加态在不同基之间不可克隆的性质,使得任何潜在窃听者的干预都必然引入可检测的扰动,从而从物理层面保障了通信链路的安全性,而这种建立在测量与不可克隆定理之上的“信息不可被窃听”原则,已从理论走向工程实现,并在全球范围内推动了量子通信网络的构建。在量子精密测量方面,量子叠加结构被用于构造高灵敏度的干涉仪器,广佛应用于引力波探测、原子钟、地质勘探等领域,通过抑制经典噪声与放大相干信号,实现远超传统极限的测量精度。
尽管如此,量子叠加在应用层面的推进仍面临诸多挑战。如何延长相干时间、抵御退相干过程、构建稳定且可扩展的测量方案,仍是量子技术工程化道路上的关键瓶颈。而在更深层次,测量问题所揭示的理论张力,也提示我们:量子力学的完备性或许尚未穷尽,对其本体论意义与演化机制的进一步理解,仍需在物理、哲学与信息科学的交汇地带继续深入探索。
然而,可以预见,随着技术的不断成熟与理论理解的不断深化,量子叠加这一源于微观世界的本质特征,必将在未来的信息处理、通信安全与精密测量等多个维度中发挥越来越广泛而深远的作用,并最终重塑我们对于“计算”“观测”乃至“现实”本身的理解。
| 























