对称性破缺,这个在物理学中听起来复杂且抽象的概念,实际上在日常生活和技术应用中有着广泛的影像。你可以把它想象成自然界中“规则”的打破,通常是从一个看似完美的对称状态,转变为一种更具独特性质的不对称状态。本文将从对称性破缺的基本概念出发,逐步介绍它在量子计算中的作用,探索这一现象如何帮助我们推动量子信息技术的前沿。

一、物理学的“隐藏法则”
对于大多数人来说,对称性似乎是一件理所当然的事情:左右对称、上下对称,甚至在自然界中,我们也经常看到这种“完美平衡”的体现。从蝴蝶的翅膀到建筑的结构,甚至到我们自身的身体对称性,这些都给我们一种直观的美感。然而,在物理学中,尤其是在量子世界里,对称性却常常不那么简单,甚至有时会被打破。
对称性破缺,顾名思义,就是打破这种原本完美的平衡状态。它常常出现在物理现象的相变过程中,比如从液体到固体的冰冻过程,或是从常温下的超导体到低温下的超导状态。换句话说,当一个系统的状态从对称到不对称的转变发生时,我们就进入了“对称性破缺”的领域。
要理解这一现象,我们可以从更简单的物理概念开始:在经典物理中,我们经常讨论一个系统的对称性——例如,球体的形状就是完全对称的,这意味着从任何角度看,它都没有变化。但在某些物理条件下,这种完美对称会突然被打破,系统可能变成更复杂、不对称的结构。这一过程不仅影响了我们对自然界的理解,还为我们提供了新的技术可能性。
在量子计算的世界里,对称性破缺展现了其独特的作用,尤其是在光量子计算的应用中。光量子计算,作为一种新兴的计算模型,依赖于量子光学的原理,并将量子位(qubit)代替传统计算中的比特。光子,作为一种量子比特,具有许多独特的性质,包括干涉、叠加和纠缠等,这些性质在传统计算中无法实现。而对称性破缺,恰恰在这类量子系统中起到了至关重要的作用,帮助我们在处理量子信息时突破了经典物理的限制。
二、从对称群到基态的变化
对称性破缺,乍看之下可能像是一个遥不可及的抽象概念,但它其实有着深刻的数学基础,尤其是通过群论和量子力学的工具来描述。在物理学中,群论是一种描述对称性最常用的数学方法,用来定义某个系统中变换的规则,这些变换能够将系统从一个状态映射到另一个状态,而不改变系统的核心性质。例如,如果我们把一个物体旋转一定角度,而物体的整体外观不发生变化,那么这种旋转就形成了一个对称性。
我们常用对称群来描述系统的对称性。对称群是指一组变换操作,这些变换在不改变系统本质性质的情况下,将系统从一个状态变换到另一个状态。举个简单的例子,对于一个球体来说,任何绕着球心的旋转变换都不会改变它的外观,因此球体具有旋转对称性。在数学上,这些旋转变换可以通过一个特殊的群来表示,称为旋转群。对称群的引入不仅帮助我们描述粒子的行为,还能通过群的表示来分析量子态的变化。群论中的每个元素(即每种变换)对应着一种对称操作,而系统的状态则可以表示为群的某种“表示”——即将群元素映射到量子态空间中的线性变换。对称性也可以通过一个“群”来表示,这个群包含了所有能使物体变换而不改变其本质的操作。对称性破缺,指的正是某种操作在特定条件下无法保持不变,从而打破了系统的对称性。
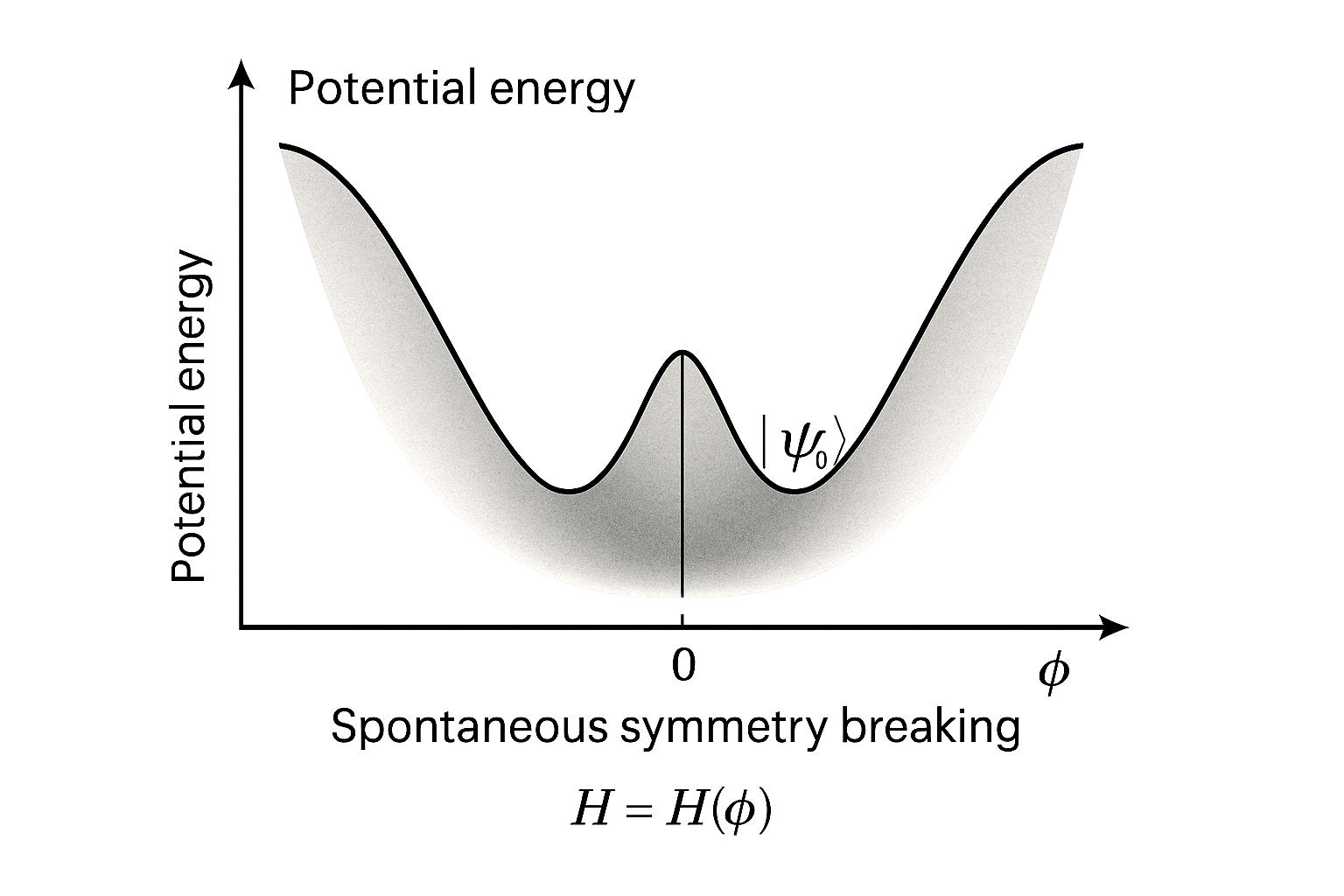
对称性破缺通常可以分为两种类型:显性破缺和自发破缺。显性破缺通常指外部作用力使得系统的对称性发生变化。而自发对称性破缺(SSB)则是在没有外部干扰的情况下,系统的本身演化导致对称性被“自发”地破坏。自发对称性破缺常常表现为一种能量最低态的选择,而这个能量最低态并不保持原本的对称性。举个例子,超导现象就是自发对称性破缺的一个经典例子:超导体在低温下表现出无电阻的特性,而这种现象是由电子对的自发形成(库珀对)所引发的,这种状态并不具备原本金属的对称性。
我们用哈密顿量来描述一个量子系统的能量。在自发对称性破缺的情况下,系统的哈密顿量通常保持对称性,但基态却展示出对称性破缺。一个典型的例子就是希格斯机制,在这个机制中,虽然存在对称的哈密顿量,但希格斯场的基态却选择了一个特定的方向,从而导致了对称性的破缺。
在数学上,自发对称性破缺通常是通过哈密顿量来实现的。假设一个量子系统的哈密顿量 H 在某些对称性操作下不变,如果系统的基态 |ψ0> 是不对称的,即在哈密顿量的作用下,基态并没有保持对称性,那么我们就可以说系统发生了对称性破缺。我们可以用以下方式表达:
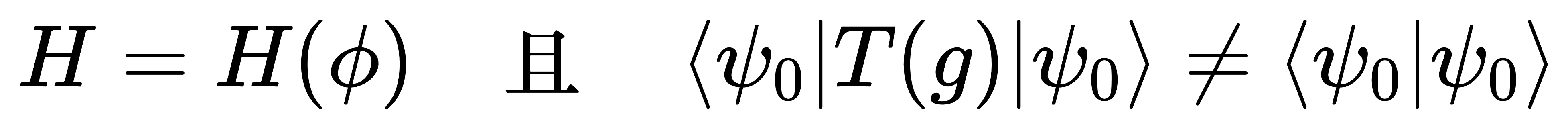
这里,T(g)是对称操作,g表示群元素,而 ϕ 是破缺的参数。这个方程表明,尽管哈密顿量在对称操作下保持不变,但基态却不具备该对称性,因此导致了对称性的破缺。
对称性破缺还与量子相变密切相关。量子相变是指系统在零温度下,由于某些控制参量(如外部场或交互作用强度)的变化,导致系统的相位发生根本变化的现象。典型的例子包括量子自旋液体、超导相变等。在量子相变中,对称性破缺通常是相变的驱动因素。例如,在超导体的相变过程中,电子对(库珀对)在低温下形成,突破了原本对称的状态,进入了一种新的、破缺对称的状态。这种破缺使得系统能够展示出新的物理性质,如零电阻。为了描述量子相变中的对称性破缺,我们可以使用量子场论中的有效场方程。对于一个自旋系统,系统的哈密顿量 HHH 可以表示为:
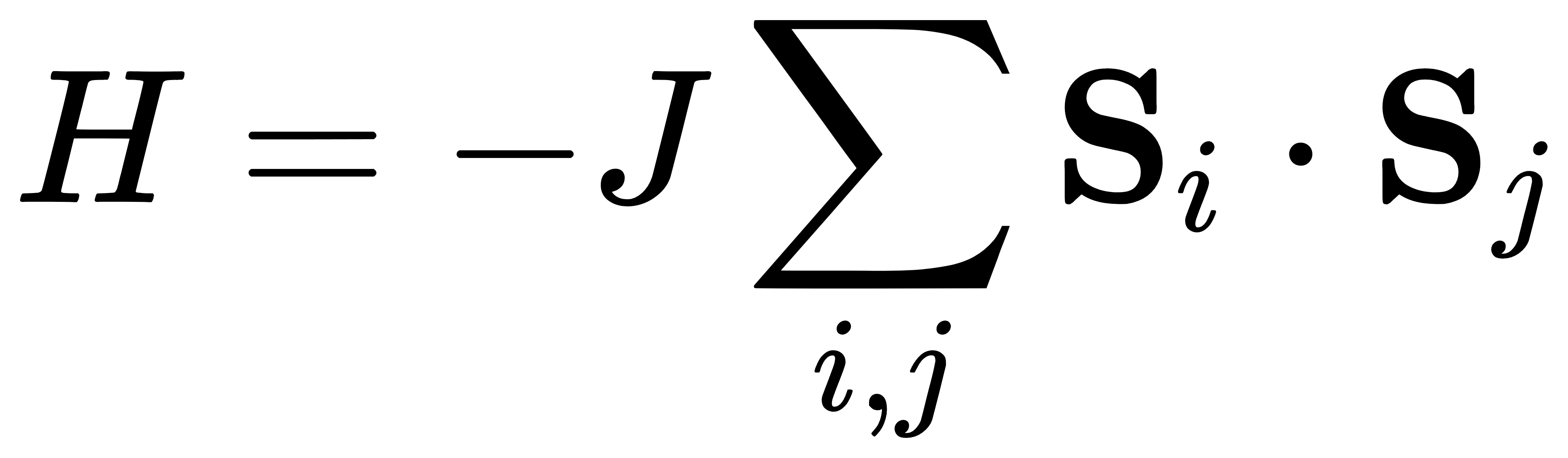
其中 Si 和 Sj 是局部自旋算符,J 是耦合常数。当耦合常数 JJJ 足够大时,系统会进入一个破缺自旋对称性的状态,从而发生量子相变。这种相变通常伴随着对称性破缺的发生,系统的基态从原本对称的状态转变为一个具有非零磁化强度的状态。
三、光量子计算中的对称性破缺:自发对称性破缺的一个示例
在光量子计算中,对称性破缺的一个重要示例可以通过光脉冲调制和量子系统的能量演化来展示。这里以光学参量振荡过程(DOPO)为例,来说明如何利用自发对称性破缺在量子系统中找到最优解。脉冲激光器通过耦合器被调制成两束脉冲序列。一束脉冲作为本地振荡光(Lo),用于后续探测输出光的相位信息;另一束则作为泵浦脉冲(Pump Pulse),为系统提供持续的能量源。光脉冲通过二次谐波产生(SHG)过程,将频率加倍,从而生成更高能量的光,随后这些光经过周期性极化铌酸锂波导模块(PPLN waveguide)再次降频调整,使得光脉冲的相位发生随机性变化。
光信号经过简并光学参量放大效应(DOPA)进行积累,最终调制成若干具有随机相位的信号脉冲。这些信号脉冲随后分为两部分,一部分进入环形腔进行进一步调制,另一部分则被引入到平衡零差探测器(BHD),该探测器将光脉冲的相位转换为电脉冲的幅度。这些电脉冲通过模数转换器(ADC)转换为数字信号,最终送入FPGA进行处理。
随着泵浦脉冲持续输入,系统的能量不断增加。起初,系统能量较低时,大多数光脉冲会在干涉相消过程中回到低光子数的状态,光脉冲的相位受到量子噪声的影响而发生翻转。然而,随着泵浦脉冲的持续注入,系统能量逐渐积累,当能量达到某一阈值时,光脉冲不再发生干涉相消的翻转,开始进入一种新的状态,这就是自发对称性破缺的发生。在这一临界点,系统从对称状态转变为非对称状态,此时每个光脉冲对应的相位配置即代表着Ising模型中的每个原子自旋的方向。这个转变不仅意味着系统进入了一个更加稳定的状态,也为后续的计算提供了最优解的初步配置。通过FPGA的读取,这些光脉冲的相位被最终传递回上位机,进而计算出最优解。
以上就是如何通过持续注入能量,使得量子系统自发地从对称状态转变为破缺对称的状态,并最终寻找到系统的最优解的过程。通过对称性破缺,量子系统能够在没有外部干预的情况下自动寻找最优解,相比传统的模拟退火算法(SA)和量子退火算法,这种通过对称性破缺实现的过程能够更快、更高效地达到优化目标。
结语
光量子计算中的对称性破缺展示了量子系统如何在没有外部干预的情况下,凭借自身的动力自发地从对称状态转变为非对称状态,并最终找到最优解。这一过程不仅揭示了量子计算中潜在的力量,也为量子算法的设计提供了新的可能性。随着量子技术的不断发展,如何更好地利用这些自发的现象,优化我们的计算过程,将是一个值得持续探索的方向。
或许,量子计算的未来正隐藏在这些微妙的量子效应之中,而我们正处于揭开这一全新计算世界面纱的起点。 | 






















