KL散度作为衡量概率分布差异的基本工具,起源于信息论中的编码问题,凭借其严格的数学定义与优良的凸性、可分解性,在统计推断、机器学习与经济测度中得到广泛应用。本文系统梳理了KL散度的推导过程、核心性质及几何直觉,并结合VAE、变分推断、困惑度评估等应用场景,探讨其实际意义,同时延伸至Theil指数等领域中的应用与拓展。
1. 引言
在信息论的语境里,不确定性并非笼统的感觉,而是一种可以精确度量的量。设想一次抛硬币实验:当硬币对每一面出现的概率都是二分之一时,下一次掷出的结果在最大程度上无法预判,这种最大的不确定性需要用一个定量指标记录下来。香农在 1948 年提出了信息熵的概念,给出了衡量不确定性的函数
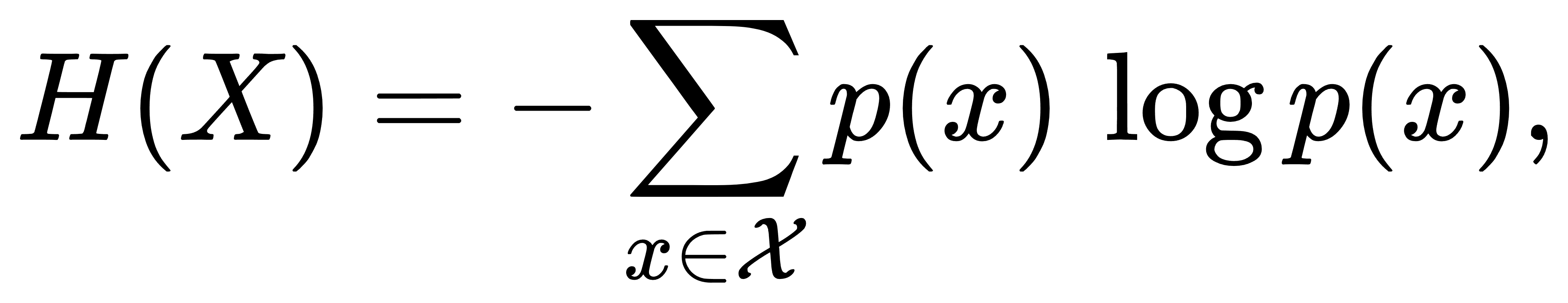
其中 p(x) 是随机变量 X 取值 x 的概率分布。这个表示式同时兼具可感知的直觉和严格的数学结构:对硬币而言,当 p=0.5时,熵达到最高点 log2;若硬币总是朝同一面落下,熵降为零,也即未来序列完全可预测的情形。
熵的提出将“不确定”转化为一个可以与资源消耗直接挂钩的数值,因为在最优编码体系下,平均码长正好等于熵。可是在工程实践里,信源分布往往难以精确掌握,我们只能用一个近似模型 q(x) 去描述真实概率 p(x)。当这种近似不完美时,为了维持无失真压缩,编码器实际消耗的比特会超出理论下限。交叉熵就出现在这种情境中:
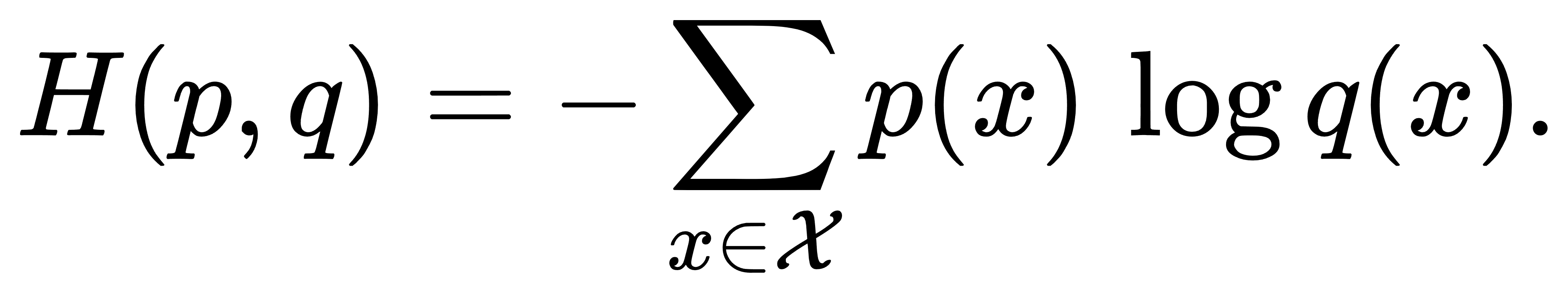
它度量的是若按照模型 q 设计码本,却用来编码真实分布 pp 生成的数据,平均需要付出的码长。当 q=p 时,交叉熵退化为熵,二者差值恰为多付出的“编码成本”。这个差额直接暴露了模型对真相的偏离,也就暗示了一种衡量分布差异的自然途径。
由此,引出信息论的一条主线问题:通过何种刻度可以精准、稳定地记录两个概率分布之间的距离?在统计、机器学习与通信系统设计等领域,这一问题的答案指向众多候选度量,而最为经典的选择是 Kullback–Leibler 散度。KL 散度以交叉熵与熵的差为定义核心,它把额外码长解释为“相对熵”或“信息增益”,并且与最大似然估计、贝叶斯推断等方法天然呼应。与此同时,因为 KL 散度天生具有方向性,一旦交换分布的位置,其数值会发生改变,使得它在几何意义上更像带方向的“箭”而非对称的“尺”。这种非对称特征在优化与推断里往往影响算法的稳定性,因此研究者又提出了 Jensen–Shannon 散度、α -散度等衍生度量去缓和 KL 的局限。
2. KL散度的数学本质与特性
在上一章中我们从信息熵和交叉熵的编码视角自然引出了相对熵或KL散度的定义,但KL散度本身的数学结构蕴含了更为丰富的性质和几何意义。首先回顾离散情形下的形式化定义:设离散样本空间为 X,真实分布与模型分布分别为 p(x) 与 q(x),则
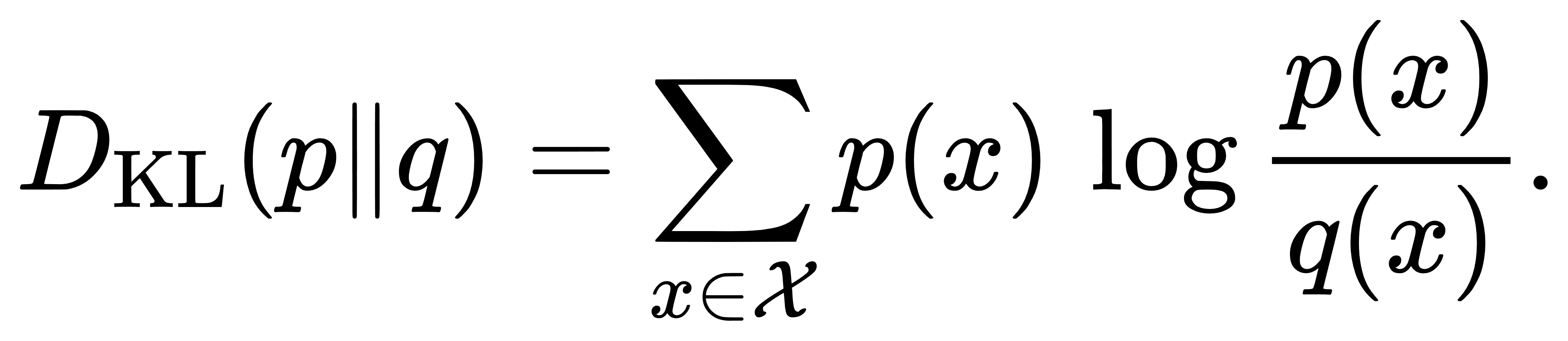
当 q(x) 较小而 p(x)较大时,log(p/q)) 将显著放大,即模型低估真实概率的严重性要付出很高的“信息代价”。
非负性定理虽然常见,但它其后还衍生出更深刻的凸性和唯一极小点性质:固定 p 后,KL散度 DKL(p || q) 视 q 为变量,是对数函数复合线性映射的结果,因此关于 q 是严格凸的。这可以通过对 logq(x) 的二阶导数求取验证:

从而保证当我们以KL散度作为目标对模型参数进行最优化时,优化问题在全局上没有非平凡的局部极小点。仅当 q(x)≡p(x) 时,散度取零,其它任何偏离都会增大目标函数值,这正是许多统计学习方法选择KL散度的理论依据。
KL散度在复合(joint)分布上的可分解性亦是一个强大工具。若我们对联合分布 p(x,y) 与 q(x,y) 考虑散度,有链式分解
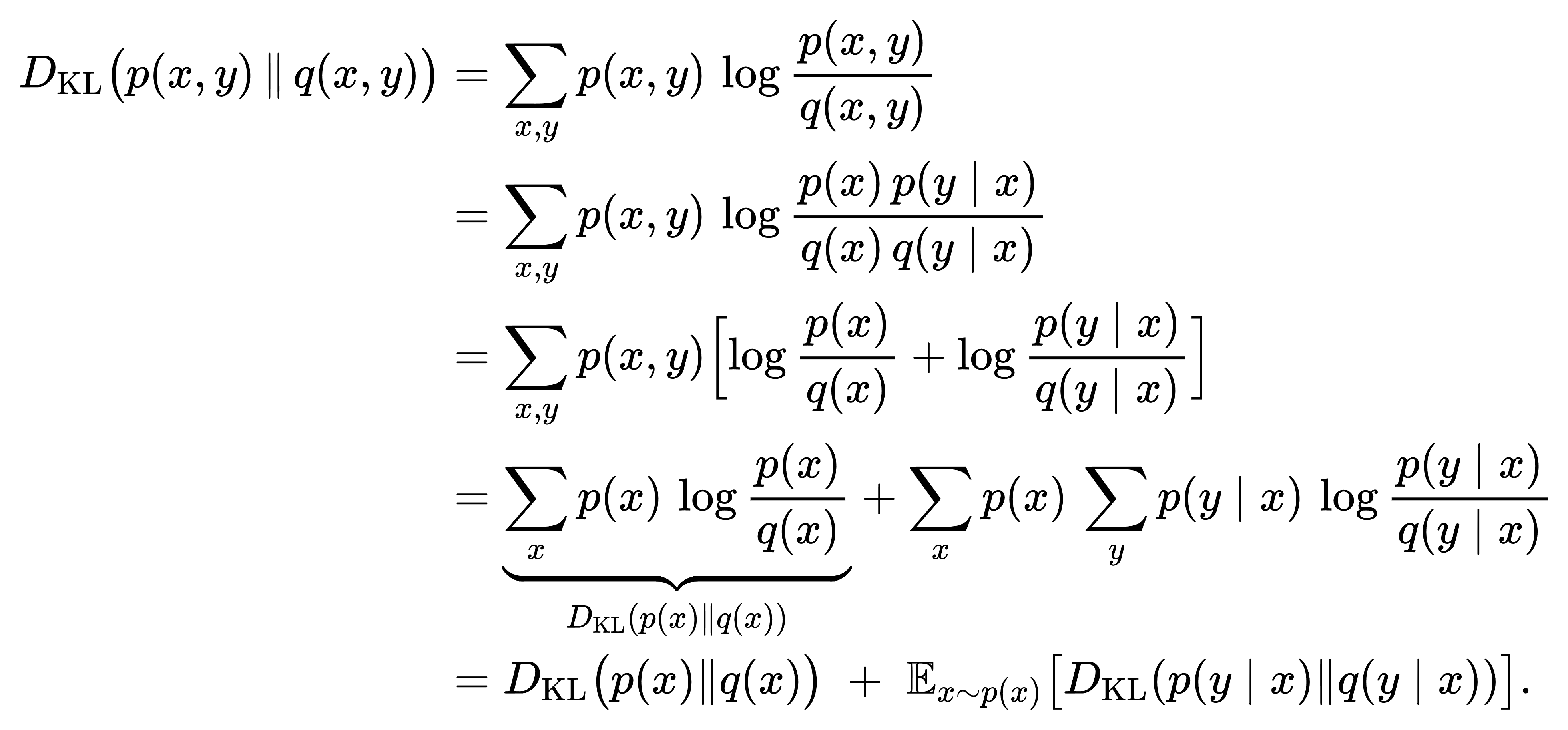
这一定理告诉我们,整体散度可拆解为边缘散度与条件散度的加权和,进而支持我们在贝叶斯网络或因果模型中逐层校准分布、在训练隐变量模型时分阶段优化下游近似。可见KL散度不仅是一个“全局一锤子量”,也能在层次化结构中发挥累积度量的角色。
将定义推广到连续分布时,只需将求和替换为积分,前提是 pp 要绝对连续于 qq,否则在 q(x)=0q(x)=0 但 p(x)>0p(x)>0 的区域散度将为无穷大。这种“支撑集不匹配”正是KL散度在实际应用中对模型覆盖能力的严格惩罚:任何对真实高概率区域的忽视都会导致无限的相对熵,使优化算法在训练时强制将模型分布涵盖到数据分布的全域。连续形式为
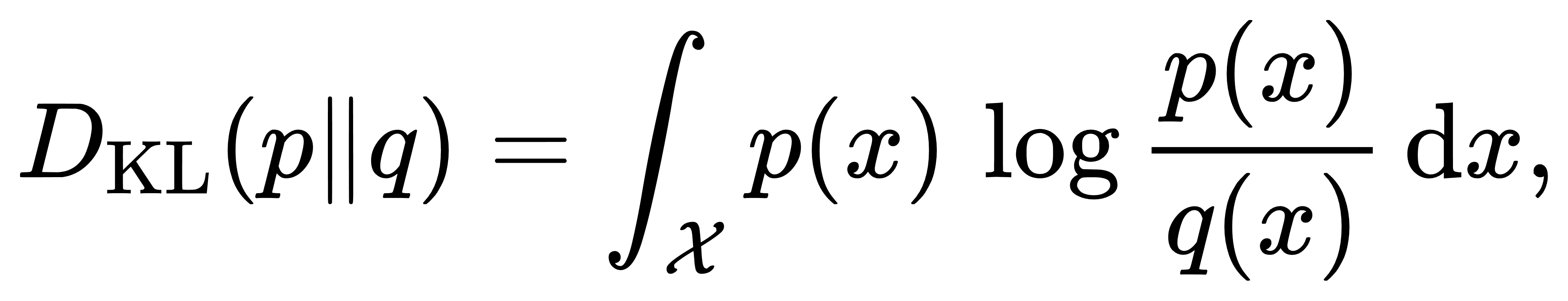
既保留了离散情形的核心结构,也在概率密度函数的阶梯变化处反映出同样的敏感性。从信息几何的角度看,KL散度可以视作一类Bregman散度。当我们取 “负熵” 作为生成函数 ψ(p)=∑p(x)logp(x)时,即可导出对应的Bregman散度恰为KL散度:
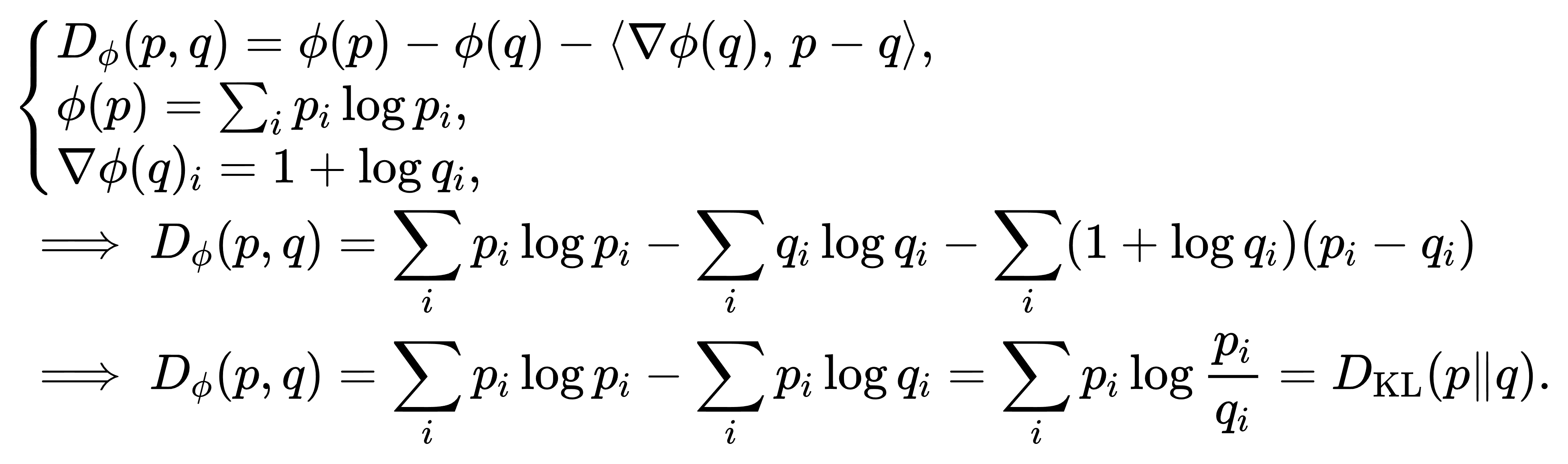
这一表示使KL散度具备了Bregman散度双凸性与零点唯一性等一般性质,并暗示在参数空间中以 p 和 q 为两端的散度能够定义一条非对称的“最短路径”——虽然并非度量距离,却具备区分度与光滑性。在参数微扰极小时,KL散度的二阶近似与Fisher信息矩阵相关:若 qθ 为参数化族,则在 θ0 处做二阶泰勒展开可得
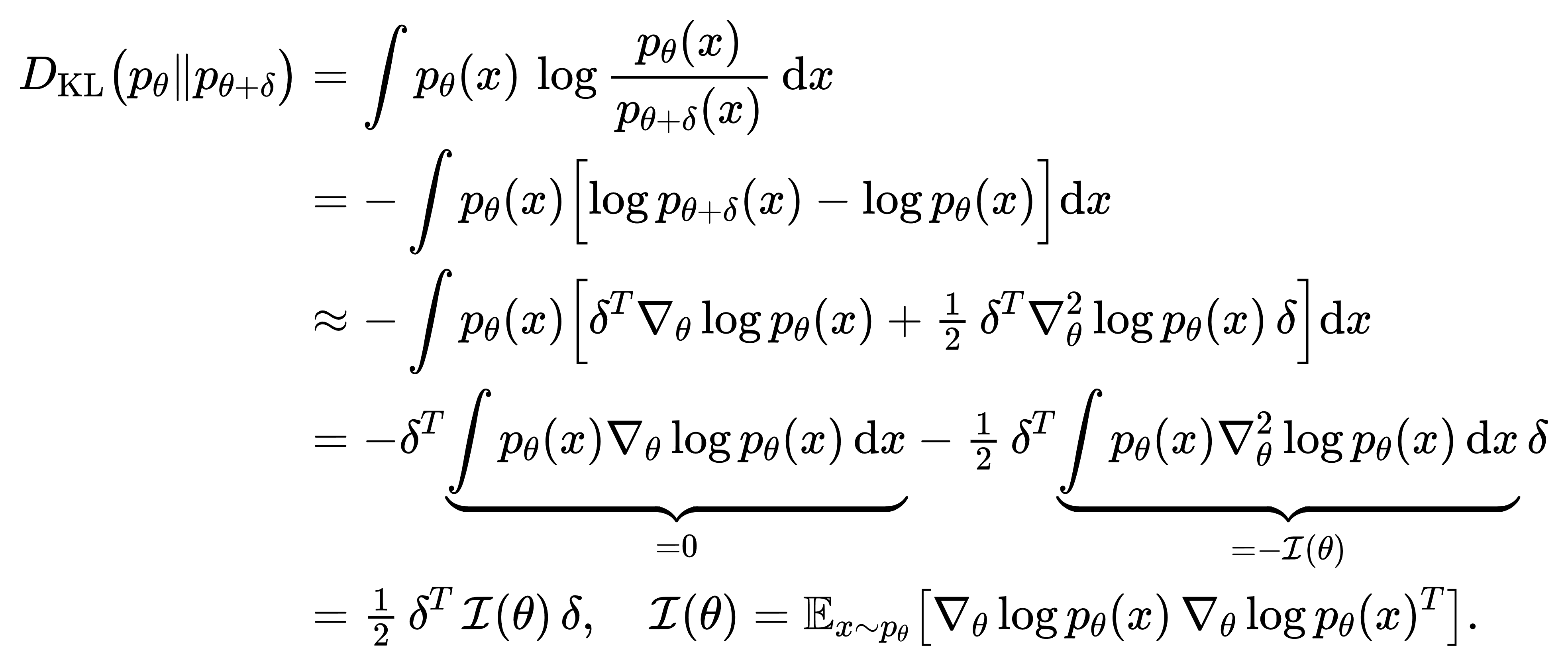
其中 I(θ)是Fisher信息矩阵,反映KL散度在统计参数空间中局部近似为一种椭圆能量范数,这一几何直觉是自然梯度法和信息几何优化的重要理论支撑。
在极大似然估计中,最大化对数似然等价于最小化 DKL(pemp∥pθ),即让模型分布尽可能贴近经验分布;而在变分推断中,又常以最小化 DKL(q∥p)为目标,将近似后验 q 拉向真实后验 p,从而得到ELBO目标函数的数学来源。不同的KL方向体现了估计方法对分布尾部或模式的偏好:DKL(p∥q) 更关注覆盖真实密度高的区域,而 DKL(q∥p) 则倾向于逼近真实分布的整体形状,往往舍弃尾部难以拟合的部分以减少散度。
3. KL散度的现实应用
KL散度虽然是信息论里的基本方法,但是在计算科学,机器学习,NLP甚至经济学中都有广泛应用。在机器学习中,KL散度常被视作衡量模型分布与数据分布偏差的“损失函数”核心。最大似然估计可等价于最小化经验分布 pemp 与模型分布 pθ 之间的散度,而在变分自编码器(VAE)里,证据下界(ELBO)的形成是由交叉熵与KL散度组合二乘的公式:
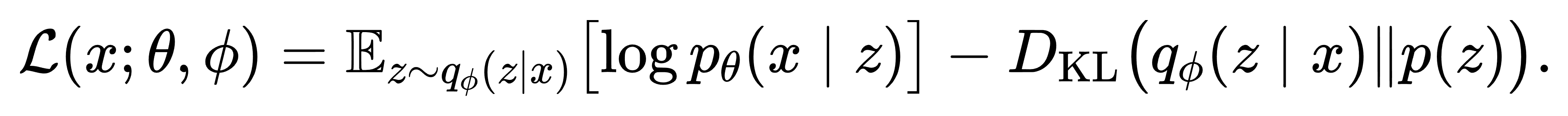
这条公式兼顾了重构质量,通过KL项将近似后验 qϕ 拉向先验 p(z),直接影响潜空间表达的连贯性与多样性。另一方面,在分类或生成任务中,经常用困惑度(Perplexity)来评估语言模型,定义为
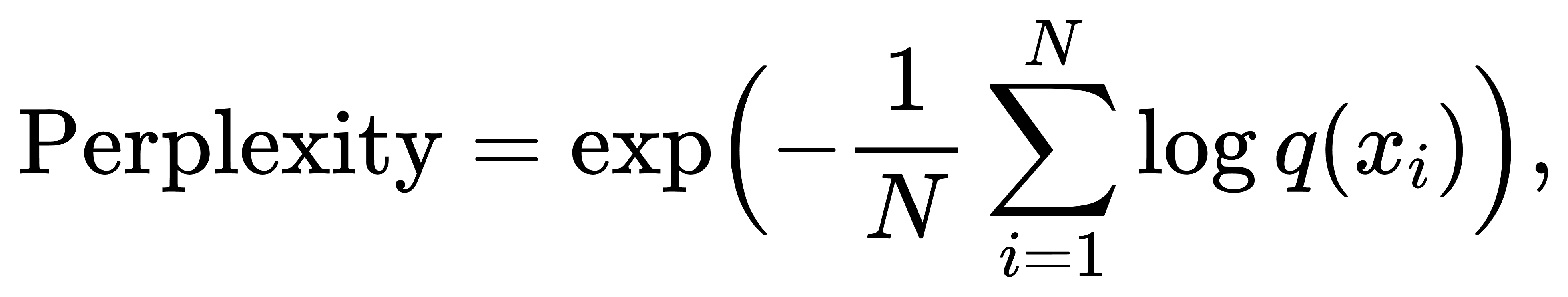
其本质也是对 pemp∥q 的指数化度量,数值越低代表分布拟合越精确。
在自然语言处理与信息检索领域,KL散度还被用于文本主题分布的比较与对齐。当一个文档主题分布与语料库主题分布之间的散度较大时,即反映该文档在内容上具有更强的个性化倾向。除此之外,最小描述长度(MDL)原则借助KL散度将模型复杂度与数据拟合紧密耦合:模型选择可视为在
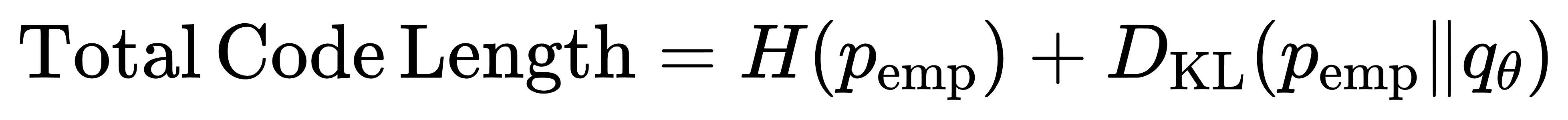
上寻找权衡点。类似地,在贝叶斯模型比较中,变分推断通过最小化 DKL(q∥p) 来逼近后验,从而使得证据下界同时成为模型证据的可计算替代。
Theil指数(泰尔指数)是KL散度在经济学上的应用之一。形式上,泰尔指数是KL散度作用于群体“收入份额分布”与“均等分配”两个概率分布之间的结果,设总体收入总额为 YY,第 ii 个个体或子群体的收入为 yi,令其收入份额 pi=yi/Y,而“均等分配”对应的参考份额为 qi=1/N (N 为个体总数或分组数)。Theil T 指数通常写作:
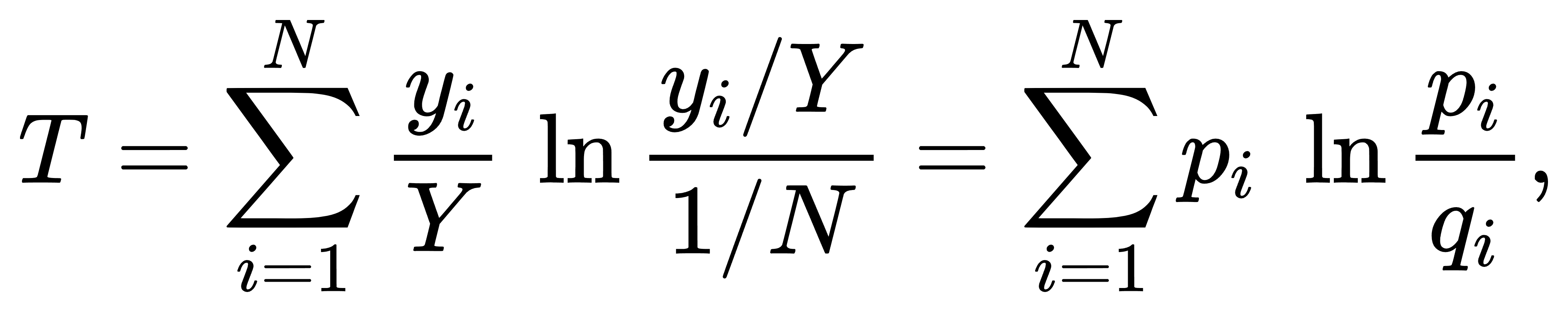
与KL散度的定义非常相近,只不过KL散度关注的是“任意两种分布”之间的信息差,而Theil T将第二分布特化为均等分配。由于KL散度具有非负、零散度当且仅当 pi=qi 时才成立的性质,Theil T 也继承了收入完全平等时指数为零、而任何偏离均等分配都会使指数严格增大的含义。
更进一步,Theil指数的可加性或可分解性也可由KL散度的链式分解得到直观解释。若将总体分为若干子群体,每个子群体内部也有自己的收入分配,则总体Theil T 指数可以拆分为“组间差异”与“组内差异”两部分,形式如
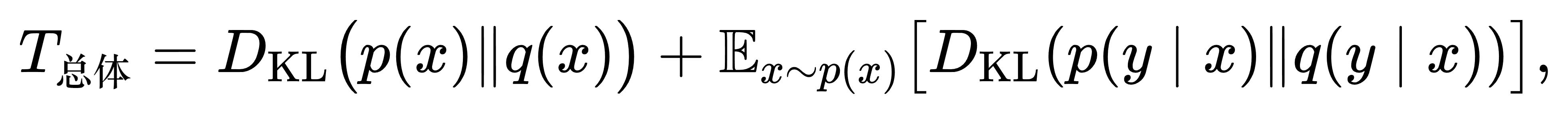
对应于KL散度的联合分布分解。因此,Theil指数不仅可用于整体不平等度量,还能深入分析分组背景下的差异来源。正如KL散度在信息几何中与Fisher信息矩阵、Bregman散度等概念相连,Theil指数也可被看作社会经济系统中“不平等信息”累积的一种度量,对政策评估和社会福利分析具有直接的理论与实践价值。
总结
KL散度以其来源于交叉熵与熵差异的定义,精准地量化了分布之间的编码成本增量。通过非负性、严格凸性与链式分解等数学性质,它不仅在理论上为模型拟合与推断提供了稳固基础,也在工程实践中广泛支持了语言建模、隐变量推断、压缩编码与社会不平等度量。随着应用需求不断增长,KL散度的局限性也促使人们发展出更对称、更稳定的度量方法,如Jensen-Shannon散度和α散度族。但无论在信息论、机器学习还是经济学中,KL散度作为一种连接统计推断与优化理论的核心量,依然保持着其不可替代的地位,也是入门机器学习的必经之路。
下一期,我们将讲讲另一位重要函数——softmax函数。 | 



























