Softmax函数是现代机器学习中最为基础却又深刻的数学构件之一,它既符合数理上的凸性、可微性要求,又能在工程实现中兼具稳定性与高效性。尽管看似只是一种“指数归一化”,背后却隐藏着信息论、凸优化与指数族统计的多重结构。本文系统梳理了Softmax函数的定义、核心性质、导数结构与其在优化中的作用。通过完整的数学推导与几何直觉,我们揭示了它不仅是“好用”的函数,更是结构精巧、理论完备的映射机制。
一、定义与应用背景
在多分类问题中,我们常常需要将模型对各类别的“打分”值映射为符合概率分布性质的输出,以便后续进行决策或评估。Softmax函数恰好满足这一需求:它先对每个实数输入施加指数运算,再将结果除以所有指数值之和,从而既保证了输出非负,也保证了归一化条件。设输入向量为 z=(z1,…,zK),Softmax映射定义为
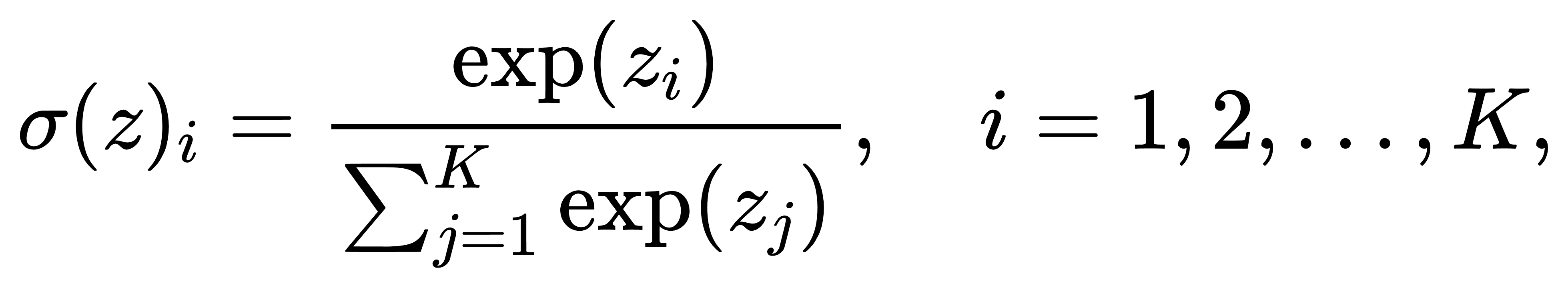
其中 exp(⋅)表示自然指数函数。由于指数运算在数值上对大输入具有快速放大效果,Softmax输出中较大的分量会得到更高的权重,而小分量则被进一步抑制,从而实现对类别打分的平滑化“放大-抑制”处理。更为重要的是,Softmax对于所有分量整体加上同一常数时保持不变,这一平移不变性在实现数值稳定的算法中具有关键作用。
Softmax的概率化特性使它成为神经网络最后一层最常见的选择。在经典的多分类神经网络中,网络输出的一组实值得分通过Softmax后即可被解释为该样本属于各类别的概率,这一解释框架与最大似然估计天然契合。此外,Softmax在注意力机制(Attention)和强化学习(Reinforcement Learning)策略选择中也扮演着核心角色:在Transformer中的自注意力中,注意力权重即通过对“查询-键”相似度矩阵应用Softmax得到;在策略梯度方法里,策略网络输出各动作的对数概率,经Softmax归一化后形成可微分的随机策略。
二、数学性质与核心定理
Softmax函数的核心作用是将实数向量映射到一个概率分布空间,这种映射在形式上看似简单,实则蕴含大量丰富的数学结构。为了深入理解这一函数,本章从概率归一化、平移不变性、log-sum-exp结构、Jacobian矩阵四个方向展开,并在每一部分中提供完整推导与结构性分析。
归一化:Softmax最基础的性质即为非负性与归一化。设 z∈RK,定义
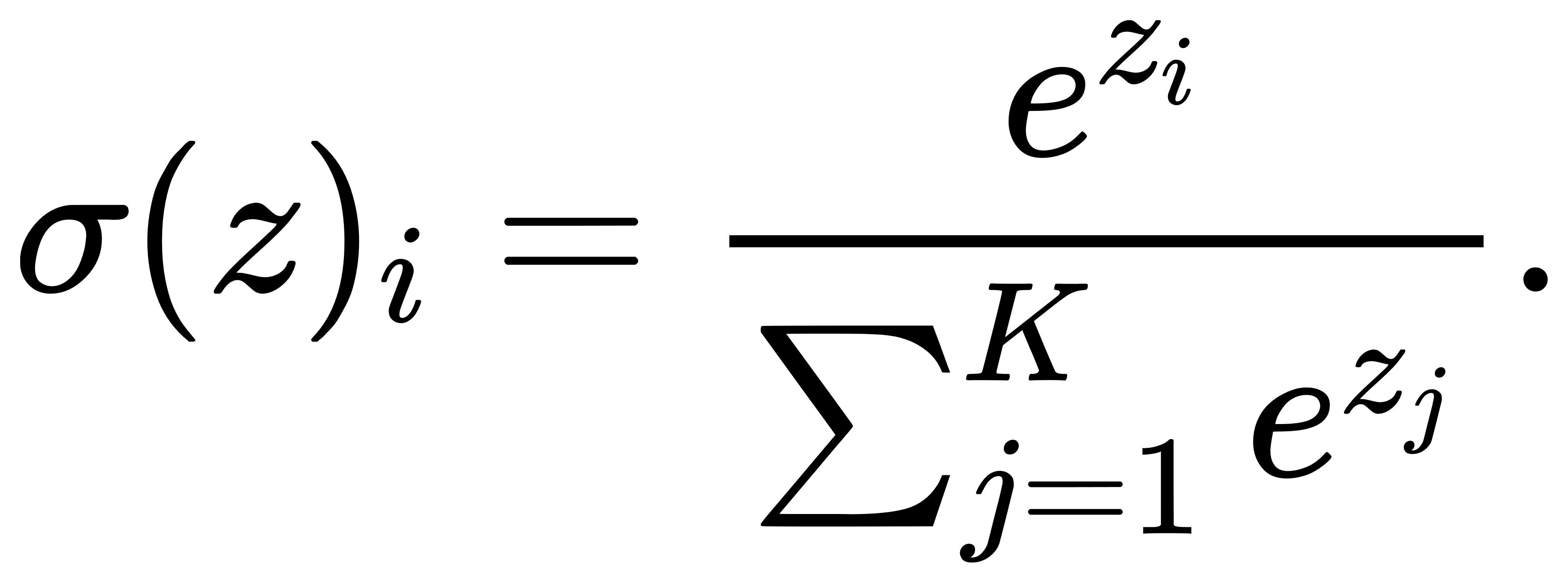
指数函数的取值始终为正数,因此对任意 i,均有 σi(z)>0。而
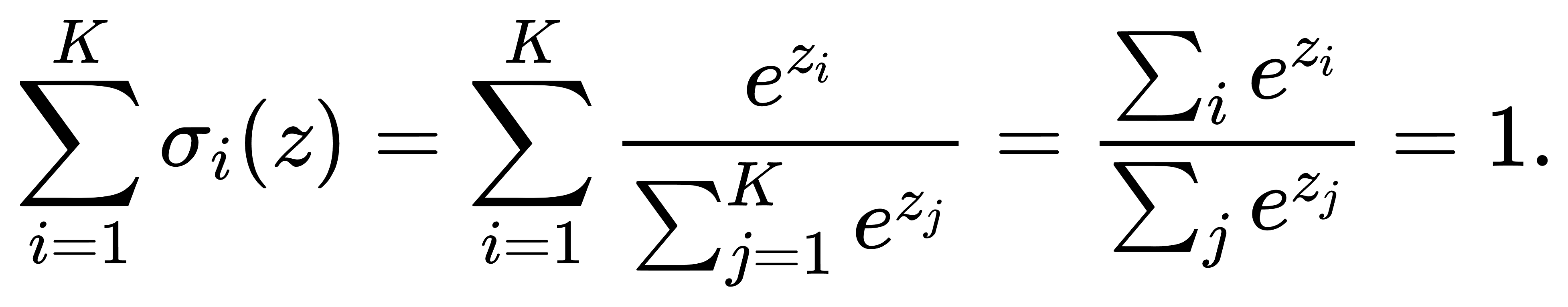
所以Softmax输出符合概率分布的定义——分量非负且总和为1。更值得注意的是,Softmax是将输入向量映射到概率单纯形 ΔK−1上的一个函数:
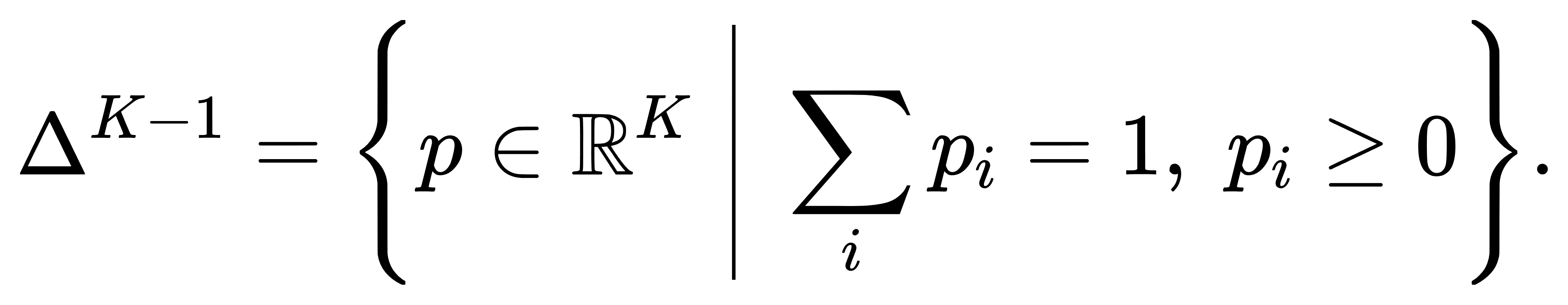
从这一视角来看,Softmax是RK到ΔK−1的一个光滑、满射(onto)映射,且映射是可微的,为后续的优化理论提供了基础。
平移不变性:Softmax另一个核心性质是对输入向量的平移不变性。即对于任意常数 c∈R,有
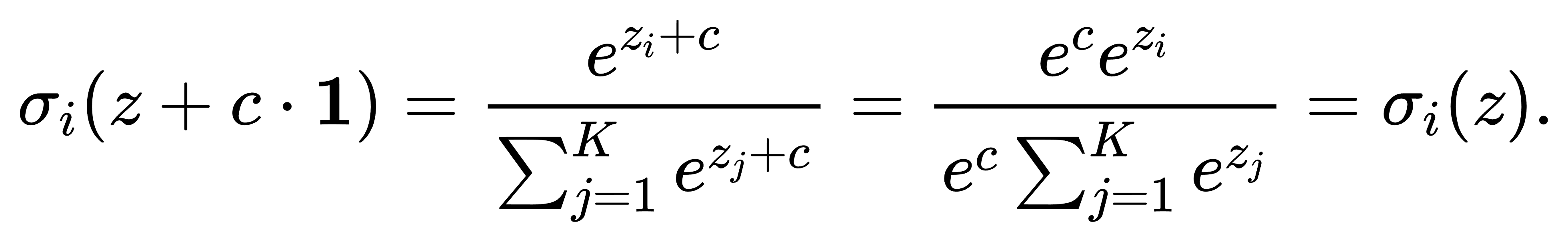
因此: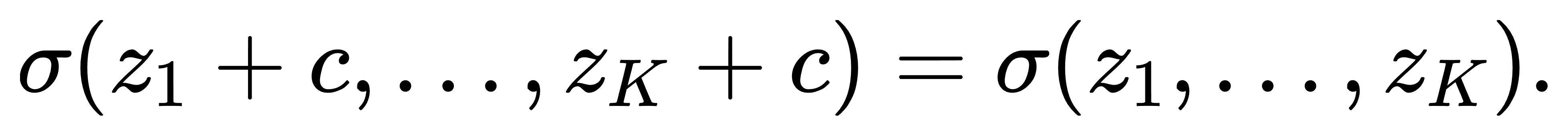
这说明Softmax只取决于输入向量之间的相对差异,而不依赖于整体的“基准高度”。这一点在数值实现中尤为关键:当输入分量较大(如在深度网络最后一层中,可能出现zi≫1的情况),直接计算 exp(zi)可能引起浮点溢出。为此,实际中常使用以下技巧: 令
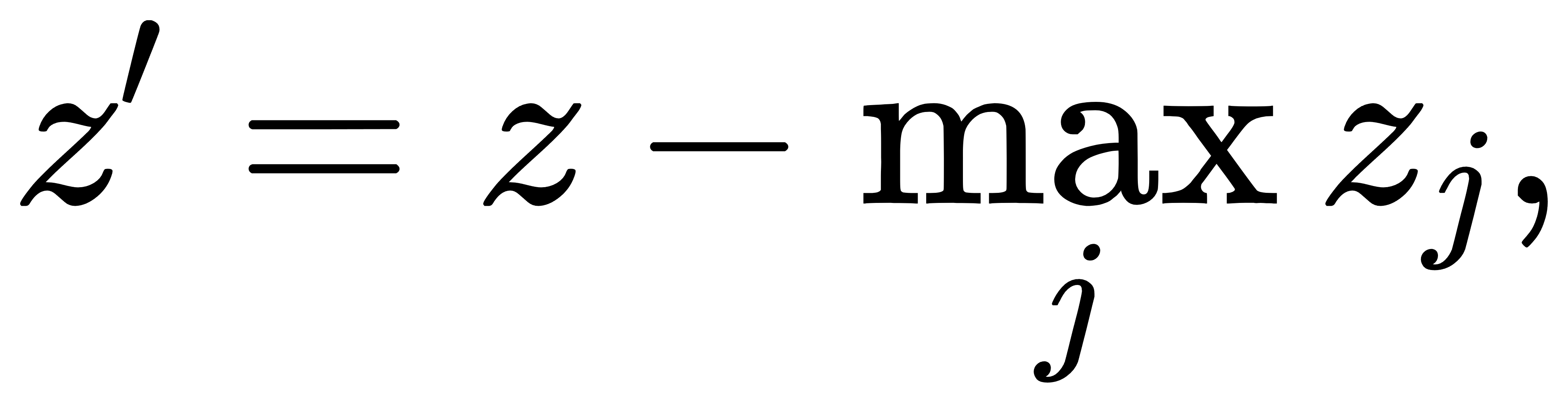
再计算:
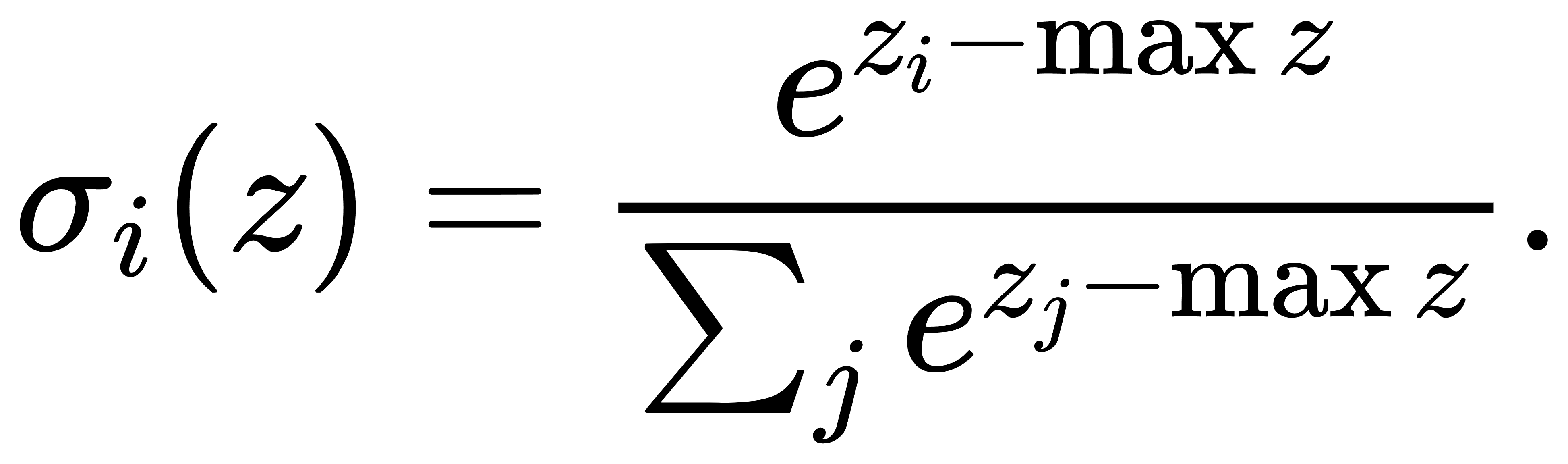
这样一来,最大值项变为 exp(0)=1,其余项都小于等于1,从而避免了数值爆炸问题。该技巧在工程实现中被称为 log-sum-exp trick 的前置部分。
与log-sum-exp函数的关系:Softmax函数可视为 log-sum-exp 函数(LSE)的梯度,其数理结构可以写作:

推导如下。设:
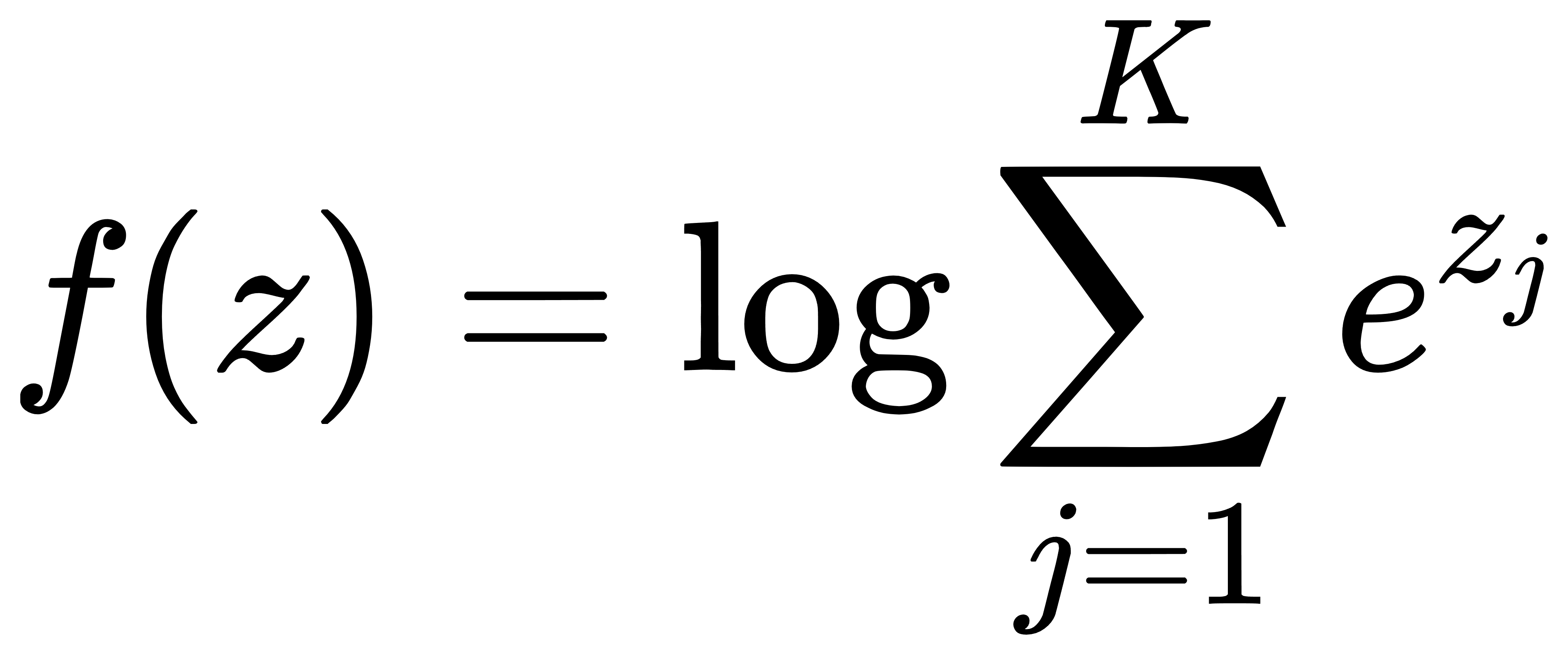
我们有
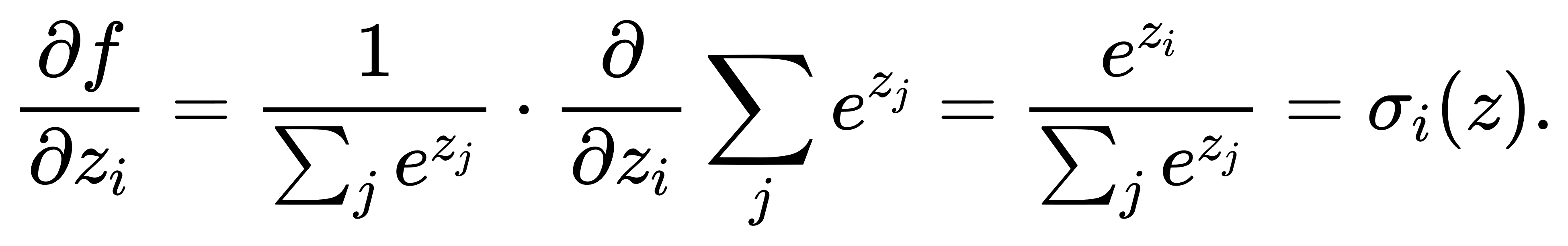
也就是说,Softmax 是 log-sum-exp 函数的梯度映射。在凸分析中,如果函数 f(z) 是凸函数,则其梯度映射具有单调性;更进一步,如果 ff 是严格凸函数,则梯度映射为单调且一一对应。我们可以验证 LSE 是严格凸的。其Hessian 可写作:
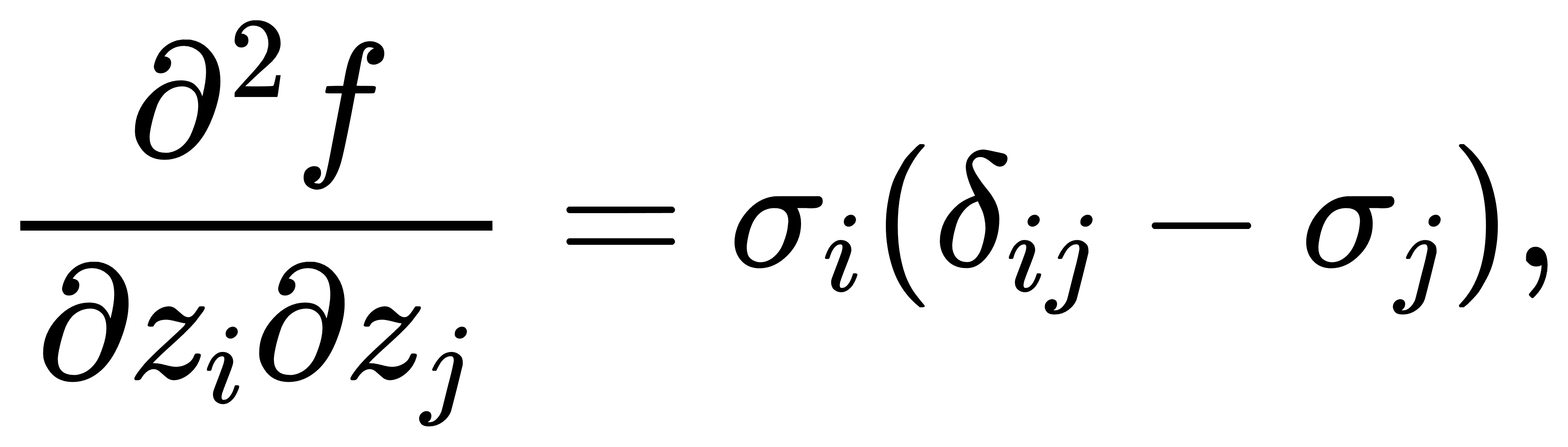
这将引入下一节的 Jacobian 分析,但在此先强调结论:LSE 的 Hessian 是正定的,因而 LSE 为严格凸函数。LSE函数本身还具有一种极限意义下的“平滑最大”性质:
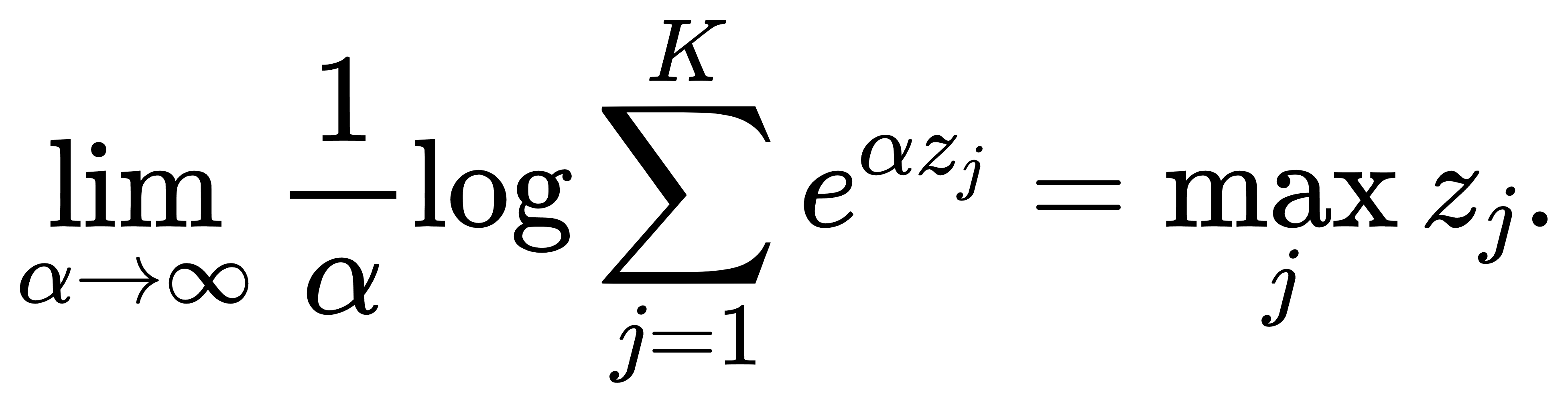
因此, Softmax 在 α 趋近于无穷时会变得尖锐,Softmax 将全部权重集中在最大项上,从而逼近 one-hot 分布。
Jacobian矩阵的结构与全耦合:Softmax的偏导数并非“单向独立”的,而是所有分量之间高度耦合。我们有:
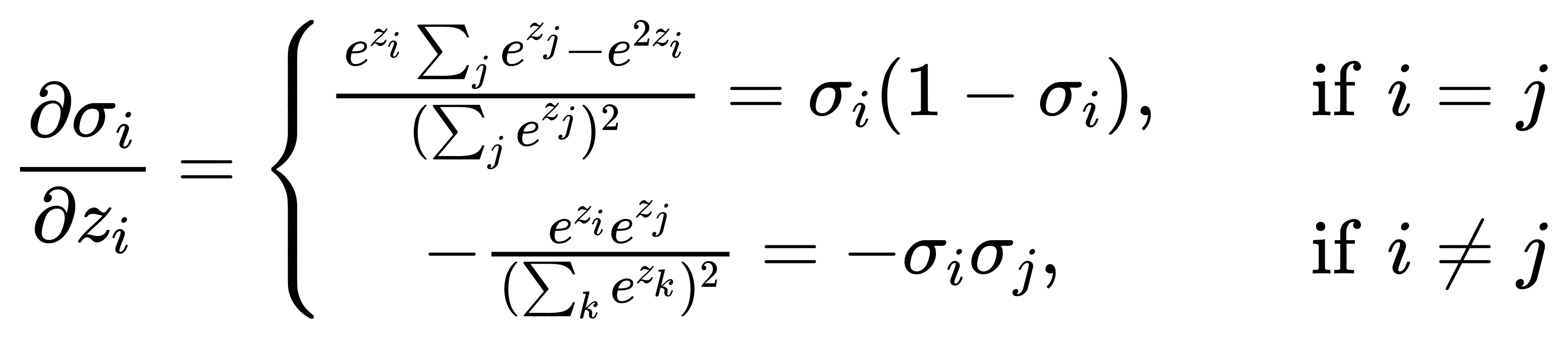
因此整个 Jacobian 矩阵为:
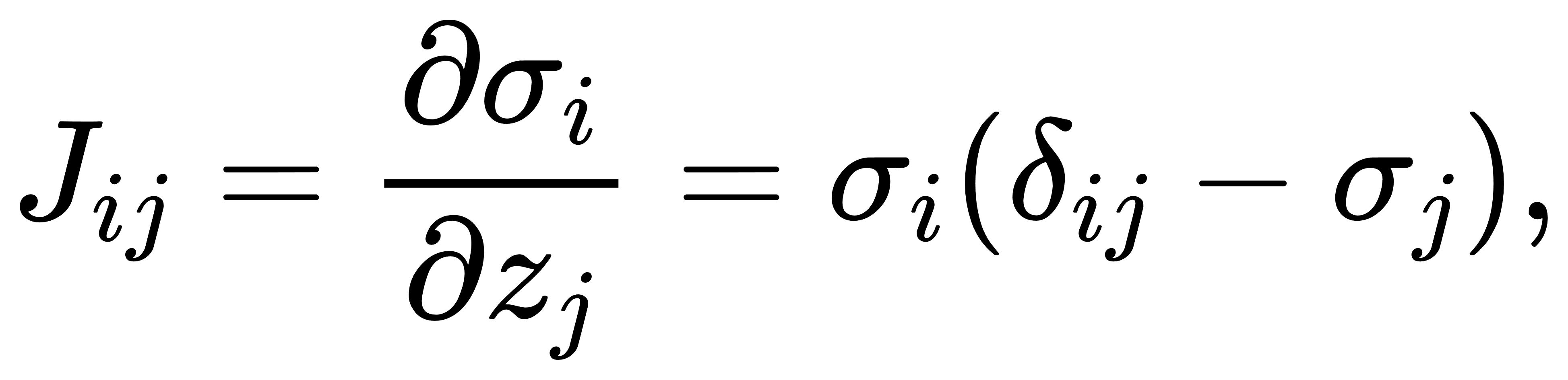
其结构为:
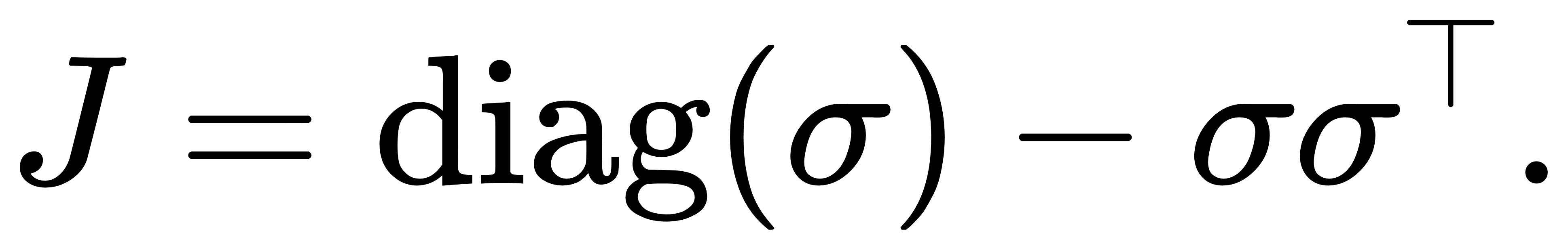
它是一个半正定的对称矩阵(对称性在 σiσj=σjσi下显然成立),每一列(或行)之和为零,且秩为 K−1,因为所有列向量线性相关(总和为零),即输出分布始终受约束。这个 Jacobian 在反向传播中起着极其重要的作用,也解释了为什么Softmax在靠近饱和区域(即接近 one-hot)时,梯度几乎全部为零,从而导致训练缓慢。
最大熵原理下的最优性:Softmax函数的另一个深层含义,来自于最大熵原理(Maximum Entropy Principle)。该原理认为,在所有满足约束条件的概率分布中,最优选择是熵最大的分布,因为它最少引入偏好,表达了“最大的不确定性”。设类别集合为 {1,…,K},我们希望选择一个概率分布 p=(p1,…,pK),使其满足某个期望约束,比如分布对给定“打分” z=(z1,…,zK) 的期望为常数:
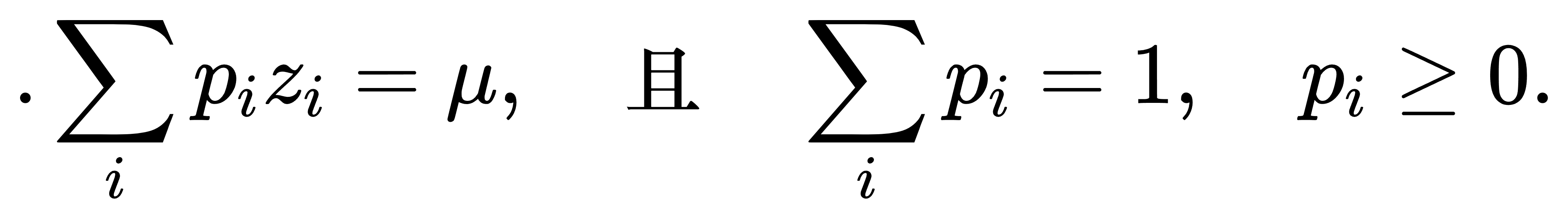
最大熵原理要求在该约束下最大化熵函数
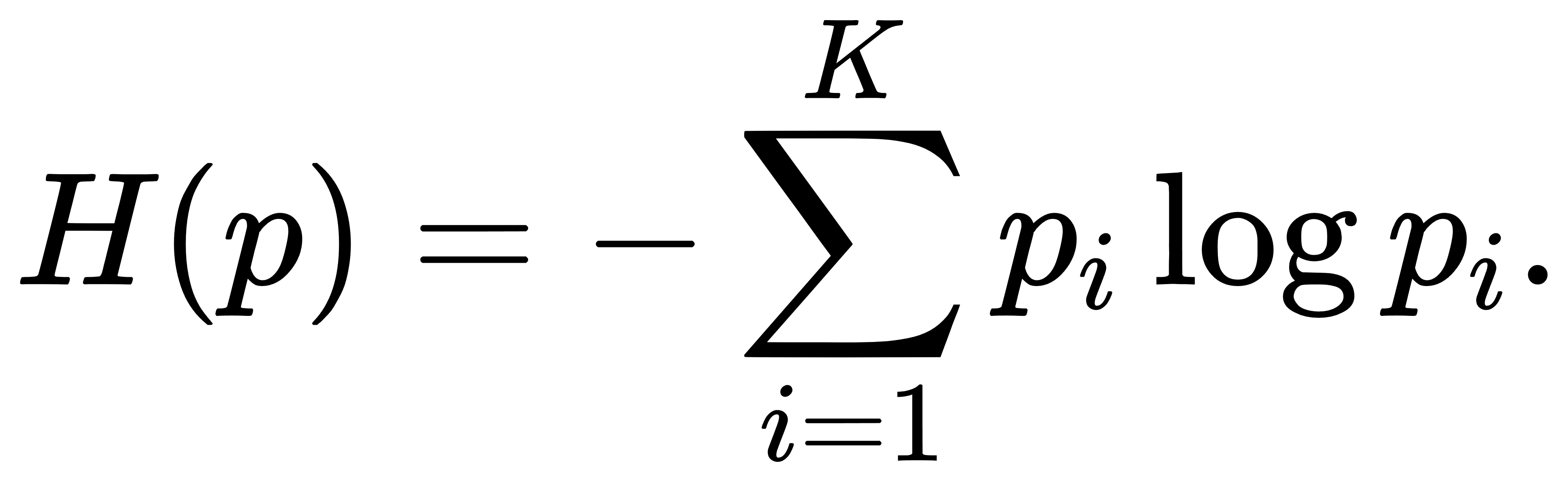
构造拉格朗日函数如下:
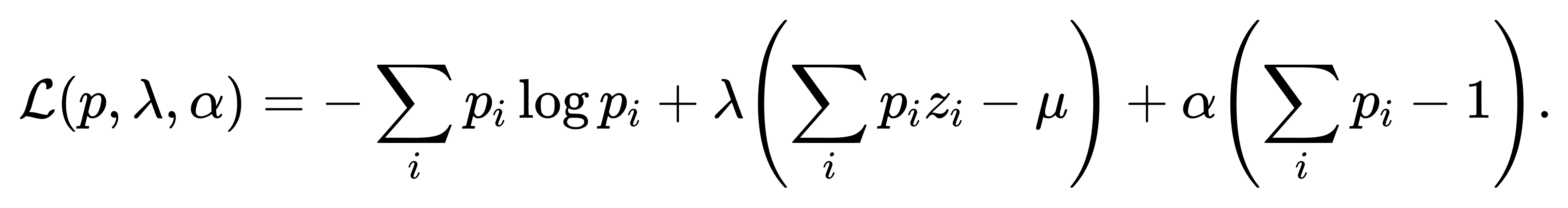
对每个 pi 求导,令其为零:
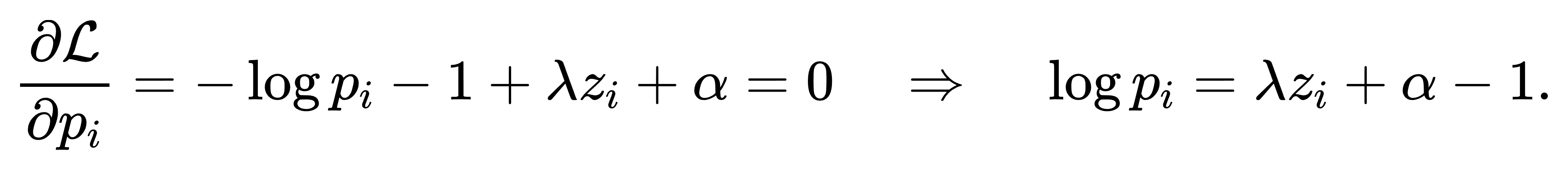
解得pi∝exp(λzi)。将 λ 视作可调缩放系数,归一化即得
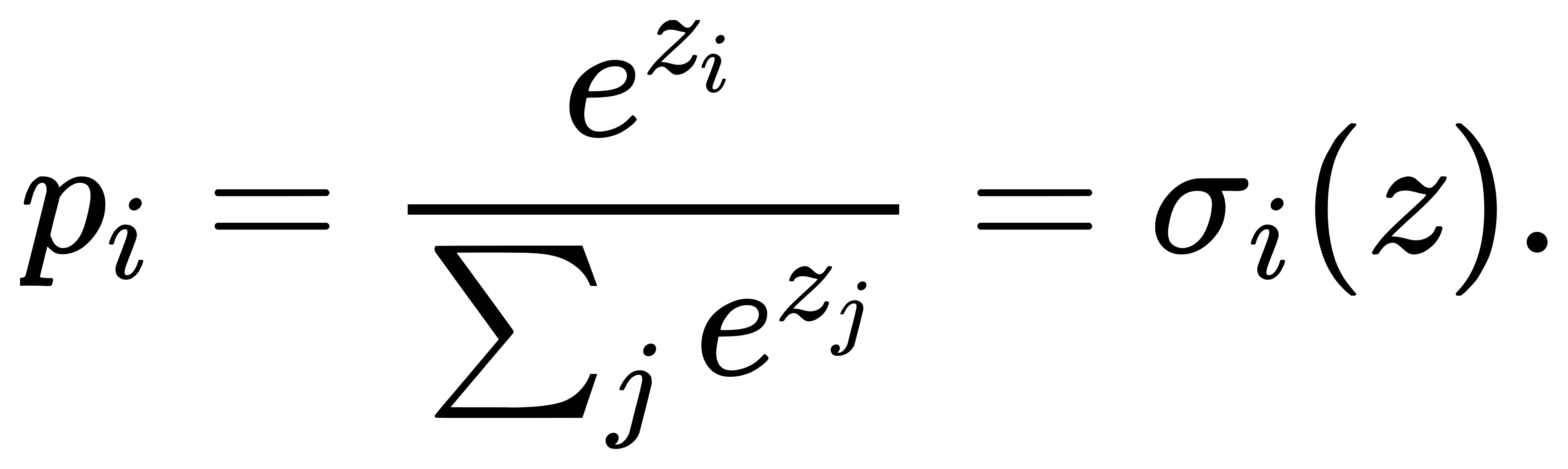
由此可见,Softmax分布是在已知“打分期望”约束下的最大熵解,Softmax严格源自一类凸最优化问题的解析解,具有自然性和最小偏见(least commitment)的统计解释。更进一步,Softmax还可视为指数族分布的一部分。在指数族的通式
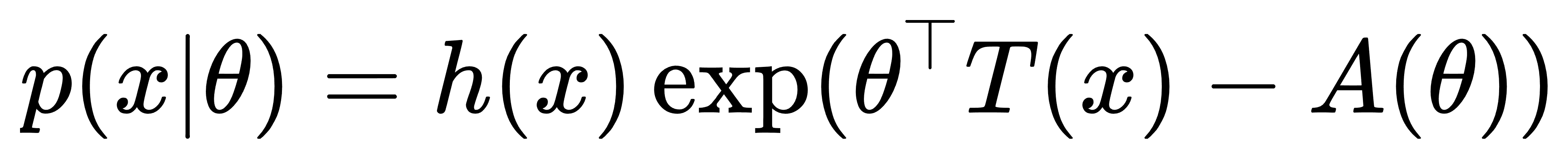
Softmax对应的是多项式分布,其充分统计量 T(x)=I[x=i],自然参数 θ=z,归一化因子为 log-partition 函数A(θ)=log∑jexp(zj)
梯度与梯度消失问题:Softmax函数虽平滑,但其在极端输入下(即某一 zi 远大于其它分量)会发生近似“one-hot化”现象——即输出接近 (0,…,1,…,0),几乎全部概率质量集中在最大分量上。在这种情况下,其梯度接近零,模型更新变慢,梯度消失线性出现。
我们可以从 Jacobian 的结构出发分析梯度范数。回忆:
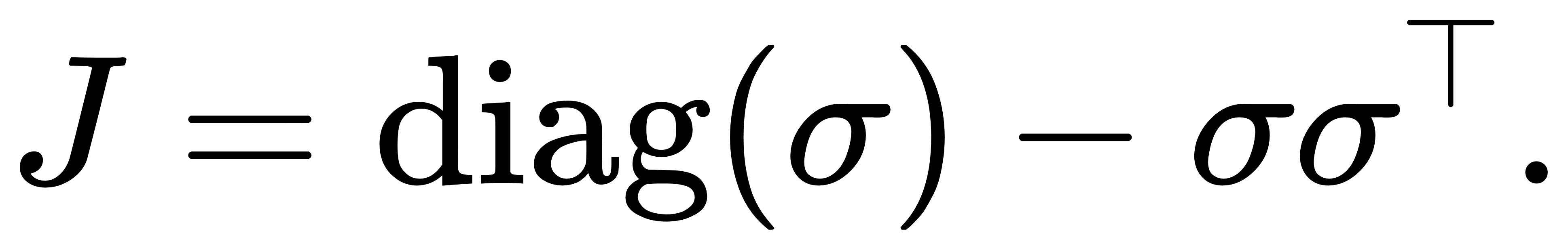
设输出为 σ=(σ1,…,σK),则对任意方向的微小扰动 δz,梯度变化为
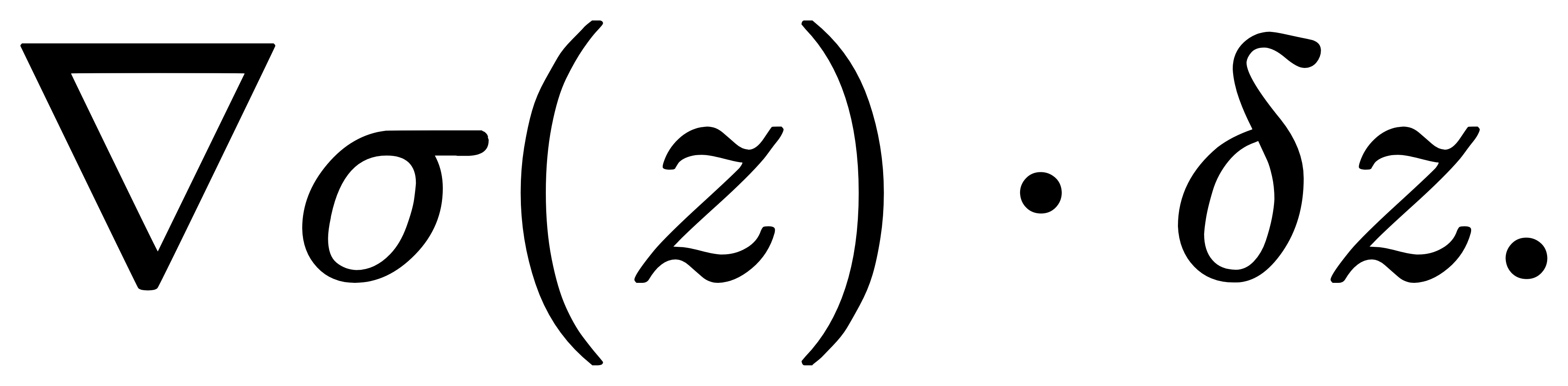
考虑梯度的 L2 范数:
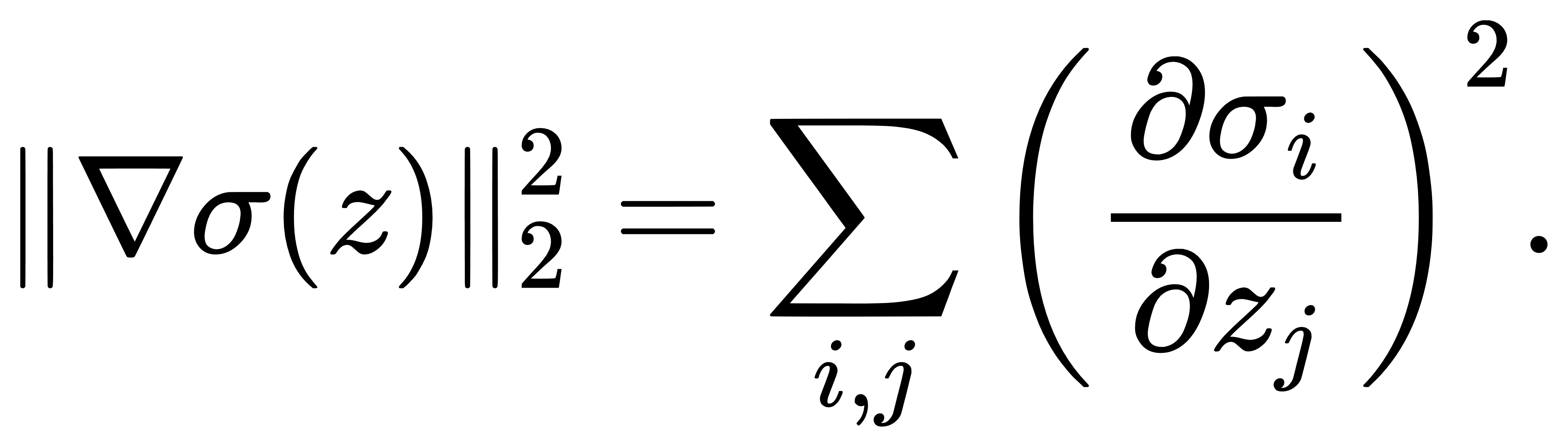
我们可以对极端情况进行估计。设 σr→1,其余趋于零,则
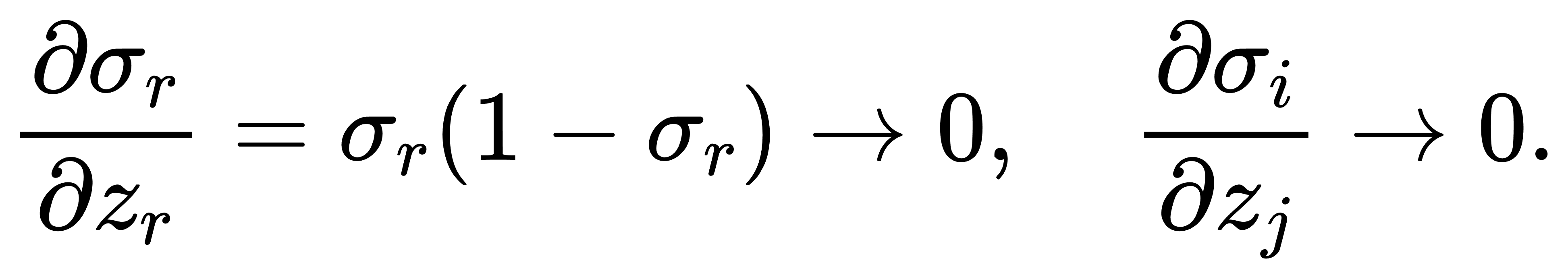
因此整个梯度几乎为零。为缓解此问题,可以引入温度调节机制(temperature scaling):
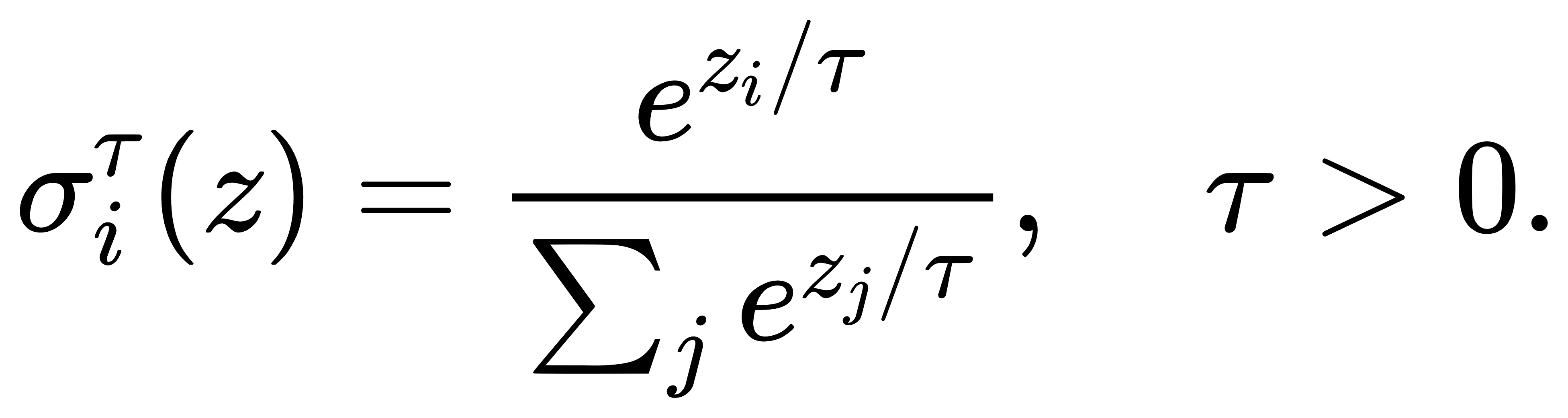
当 τ→0\,Softmax变尖锐,趋近于 argmax;当 τ→∞,Softmax输出趋于均匀分布。通过调节 τ 可控制模型的“信心水平”,在训练早期使用较高温度(以鼓励探索),在蒸馏、迁移、策略融合中调整温度以平衡保守与冒险。特别地,在知识蒸馏(Knowledge Distillation)中,教师模型往往输出温度较高的Softmax概率分布,从而向学生传递“类间相似度”的细腻结构,提升泛化能力,这类“软标签”往往比one-hot标签包含更多信息。
三、Softmax函数与交叉熵的梯度结构
Softmax函数最为人熟知的用途,是在神经网络的分类任务中作为最后一层激活函数,并与交叉熵(cross-entropy)损失函数共同使用。表面上这是一种工程设计上的经验搭配,但从数学角度来看,两者的结合极为紧密,尤其在反向传播中显著简化了梯度计算结构,成为现代深度学习中的一种“结构性优化”。
交叉熵损失函数与最大似然:假设我们有一个K类分类问题,模型对输入 x 输出打分向量 z=(z1,…,zK),通过Softmax变为类别概率分布
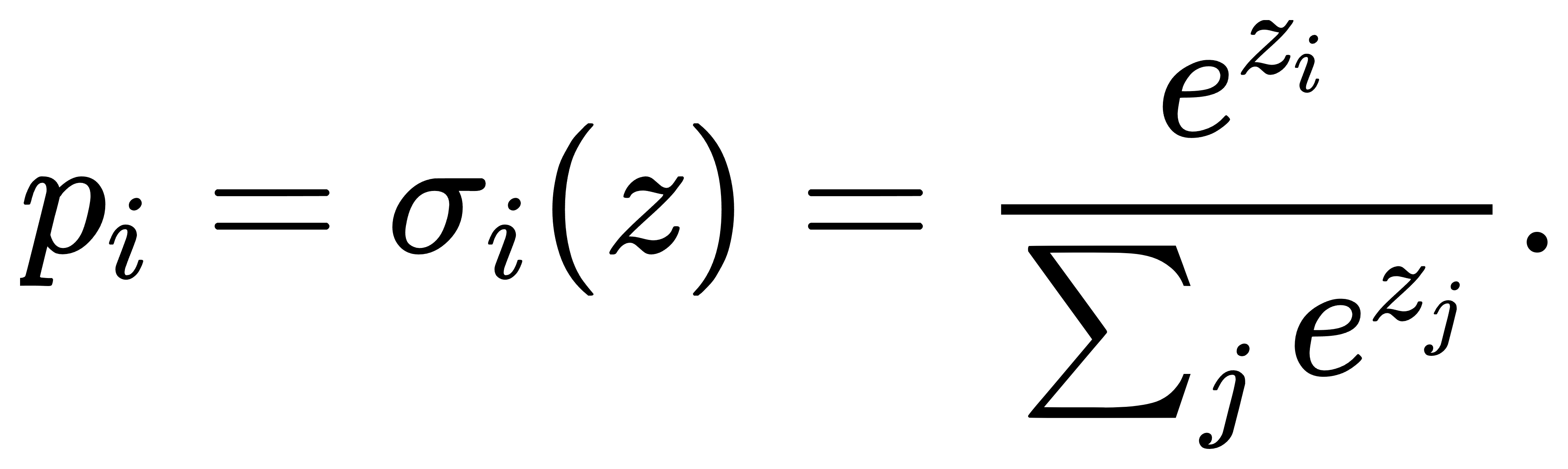
而数据的真实标签为 one-hot 向量 y=(y1,…,yK),其中仅有一个分量为1,其余为0。交叉熵损失函数定义为:
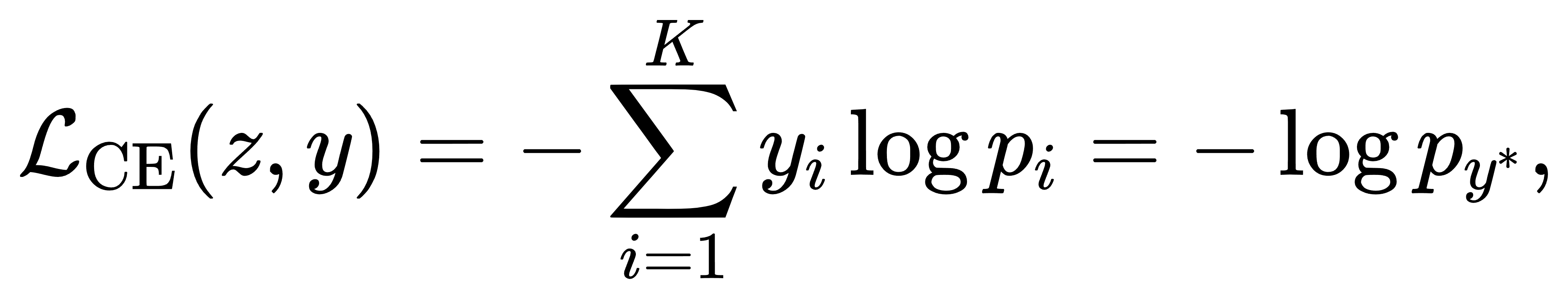
其中 y∗ 是真实标签所对应的索引。该形式恰等价于最大似然估计下的负对数似然损失,即使模型预测概率越靠近真实标签,损失越小。
Softmax + 交叉熵的梯度:设损失函数为
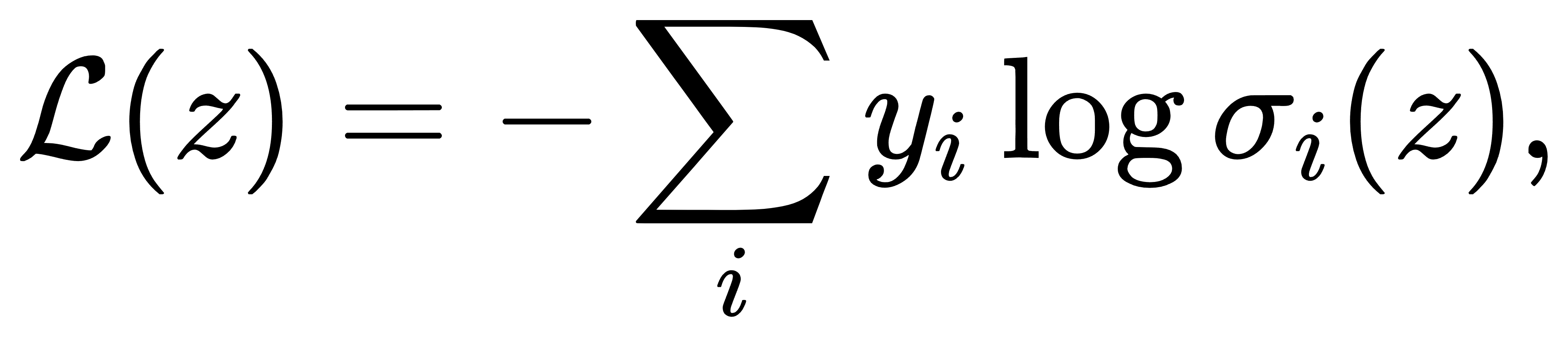
注意,Softmax与交叉熵均依赖于 z,所以需要链式法则处理。首先 recall Softmax 的导数形式(上一章结论):
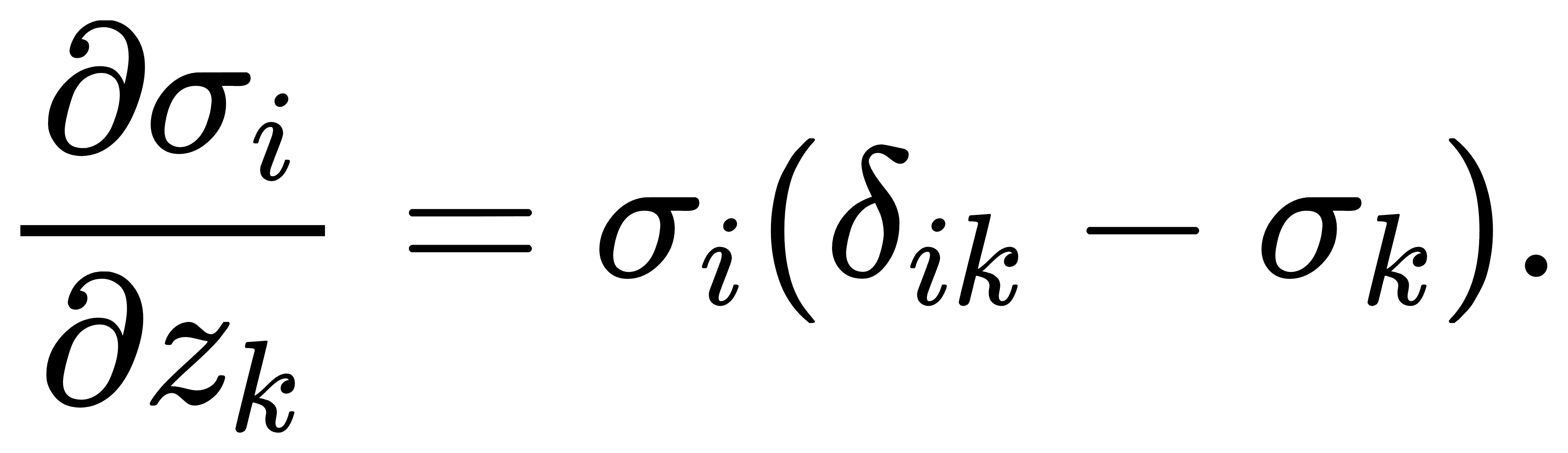
所以我们有:
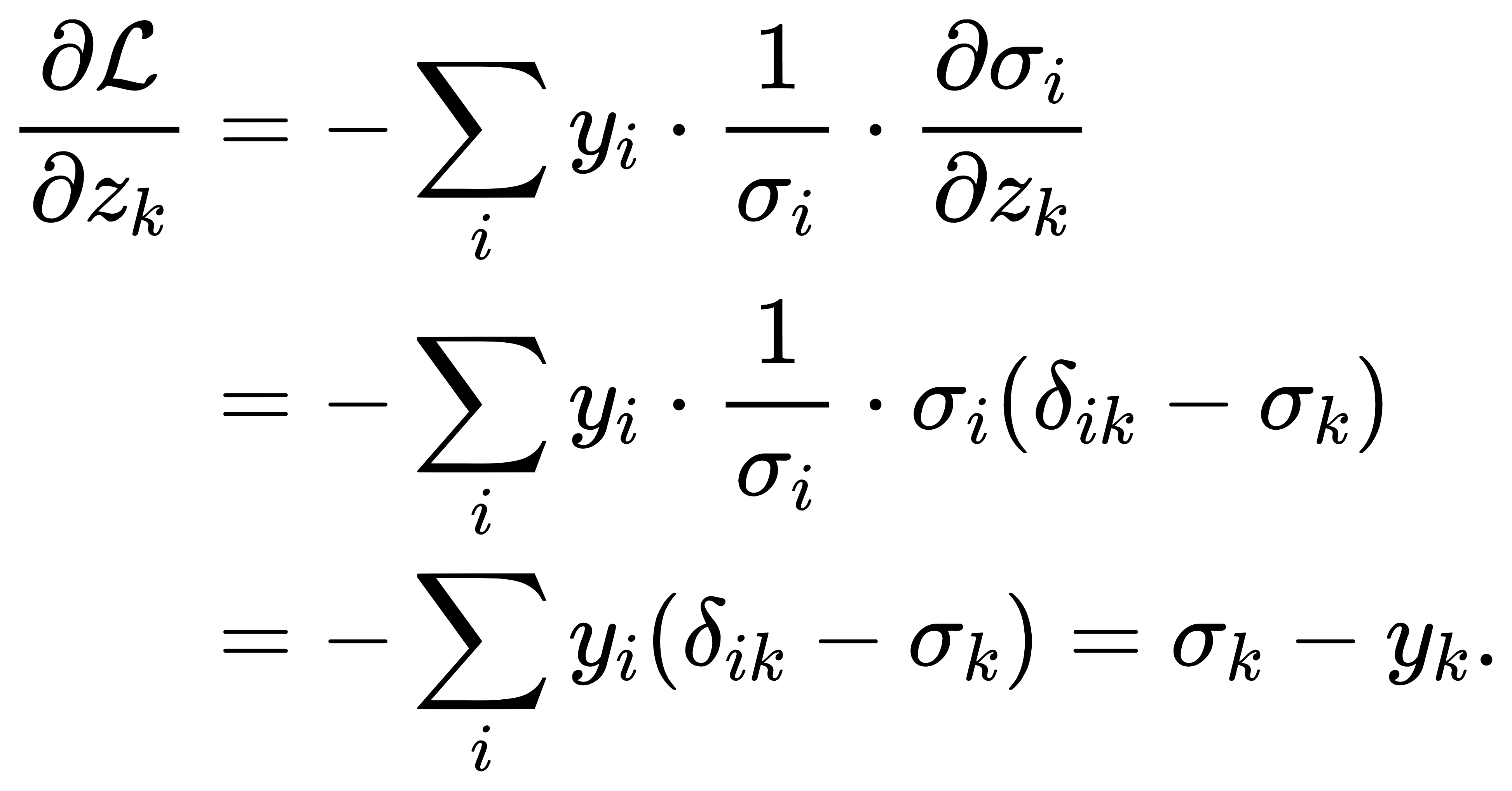
即
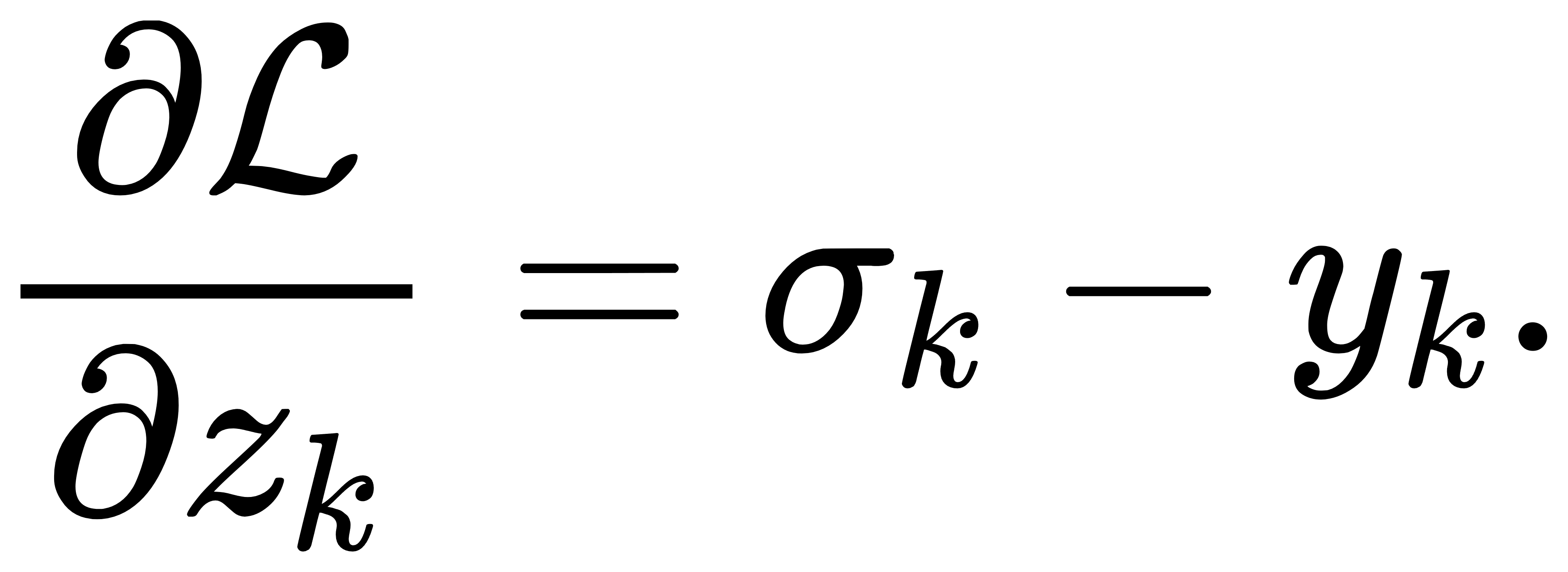
该式极为简洁,且高效可计算。在实际神经网络中,该公式广泛用于后向传播阶段,使得Softmax+交叉熵可以看作一个整体支持反向传播的结构单元,避免了分别求导带来的复杂张量操作。上述推导也可以更紧凑地写作矩阵向量形式。令σ(z)=p为Softmax输出; y 为真实标签 one-hot 向量;以及L(z)=−y⊤log σ(z)。 则梯度为:
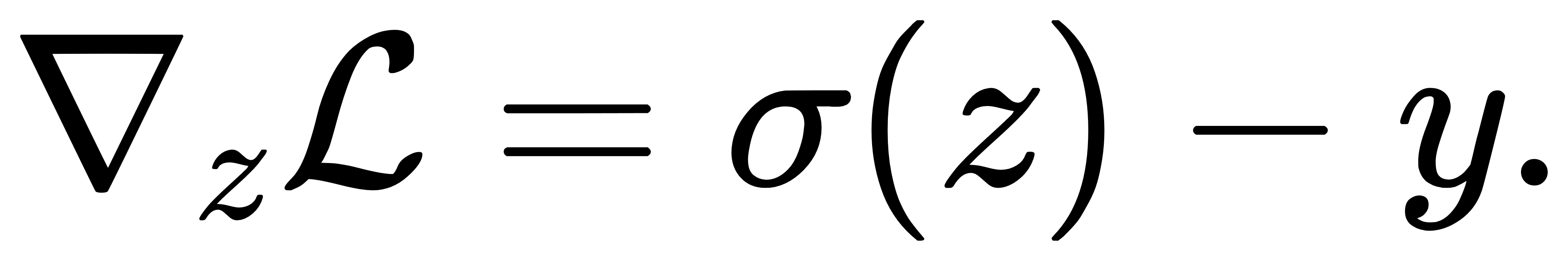
由于 one-hot 标签中仅有一个分量为1,Softmax 输出中只需要对该位置的概率进行 −log p计算。更进一步,在 mini-batch 情况下,设每个样本为 z(n),则整个批次的梯度为
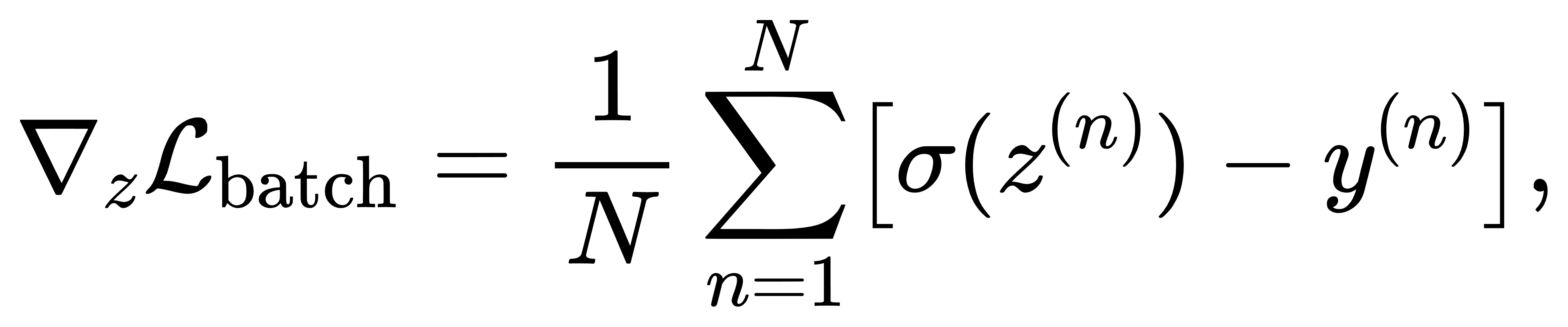
这不仅可直接用于矩阵运算加速,也具有稀疏性友好结构,即只对少量维度的输出产生有效梯度。Softmax输出趋于饱和(即某一分量趋近1,其余趋近0)时,梯度变为
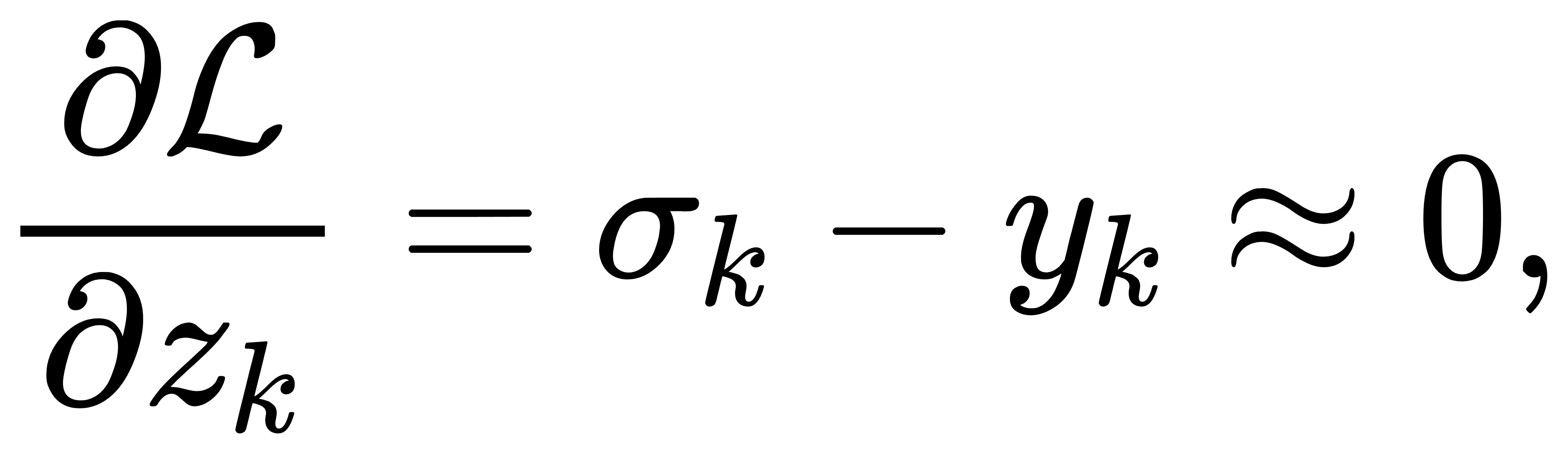
除非 k=y∗,此时若模型预测极端错误,即 σy∗≪1,则

因此在错误类别上梯度接近0,正确类别上梯度趋于-1,形成一种梯度稀疏的结构。这有利于快速收敛,但也导致梯度爆发/消失现象对不同样本影响不一,在早期训练阶段尤其需要注意学习率设置与梯度裁剪策略。
虽然Softmax函数本身是非凸的,但当与交叉熵组合为一个整体损失函数后,在输入 z 的空间中,该函数关于 z 是凸的。因为我们可以将
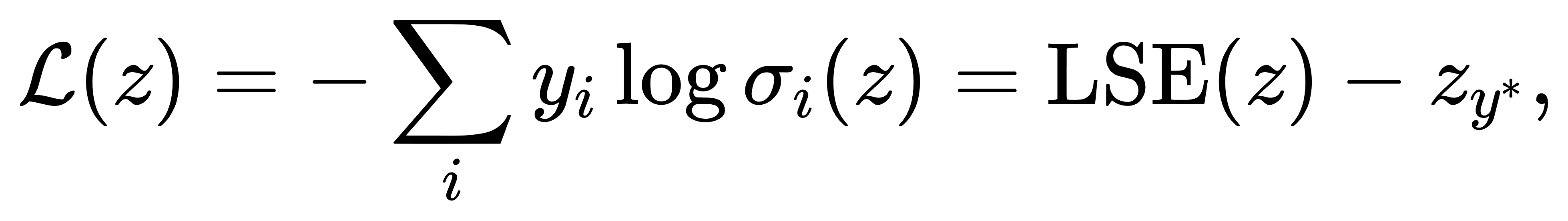
其中 LSE(z) 是 log-sum-exp 函数,为严格凸函数,zy∗ 为线性项,所以整个损失函数对 zz 是严格凸的。这一性质表明,若网络最后一层为线性层(即 z=Wx+b),则输出层的优化问题为凸优化问题,从而不存在局部极小点,利于收敛。
四、Softmax函数不足及变体
尽管Softmax函数在多分类任务中表现出色,其结构稳定、计算可微、梯度简洁,但随着应用场景扩展与模型规模增长,人们也逐渐意识到标准Softmax在效率、表达能力、梯度结构等方面存在局限。尤其是在以下几类问题中:①输出空间极大(如百万级词表的语言模型)导致计算开销巨大; ②标签高度不平衡,Softmax对低频类学习不足; ③输出需要具备稀疏性或可解释性,而Softmax始终输出非零概率; ④模型需要在保持可微的同时处理离散采样操作。为了一定程度上解决这些不足,研究者在Softmax的变体上绞尽脑汁,以提升其泛化能力,适应更特殊的数据结构。限于篇幅,本文仅列举部分常用的Softmax变体如下:
Sparsemax(稀疏Softmax):将Softmax输出压缩为一个真正的稀疏概率分布,使部分分量严格为零,提升可解释性与压缩效率。
Entmax(包含Softmax与Sparsemax为特例的一族函数):以Sparsemax和Softmax为特殊情况的广义族,包含一个幂参数 α,在稀疏性与光滑性之间建立连续控制。
Gumbel-Softmax / Concrete分布(用于可微分的离散采样):为处理离散变量的梯度优化问题引入的重参数化技巧,允许在保持可微性的同时对类别进行采样。
Adaptive Softmax(用于超大词表下的分层加速):针对极大输出空间的加速结构,通过层次化或近似分组降低Softmax计算复杂度。
Logit Normalization / Label Smoothing(虽不是函数变体,但对Softmax行为具有结构性影响):通过修改目标分布或损失结构,改善泛化能力或对抗过拟合。
总结
Softmax函数之所以在现代机器学习中屹立不倒,不仅是因为它提供了概率化输出的自然形式,更在于它深刻嵌入了优化理论、信息论与统计建模的核心框架。从其与log-sum-exp的连接,到最大熵解释,再到与交叉熵组成结构性简洁的反向传播公式,Softmax在数学结构上展示了极高的内聚力。同时,其众多变体为模型在稀疏性、效率与可解释性等方面提供了有力补充。在大规模模型、多任务建模与深层结构中,Softmax依然是最稳定且可靠的构建单元之一。真正理解它的结构,也正是掌握现代神经网络建模本质的一步。 | 



























