本帖最后由 Dorian 于 2025-6-10 11:42 编辑
一篇充满争议的博士论文,如何变成横扫AI、物理、社会学的万能钥匙?伊辛模型藏着怎样的跨界密码?从磁性到智算,从饱受质疑到大放异彩,伊辛模型用一百年证明,在时间的高温洗礼下,唯有真金不怕火炼。
在物理学的发展长河中,有些理论模型的诞生往往源自一个朴素的问题:我们如何理解日常生活中司空见惯的现象?比如磁铁。它为何会吸附金属?其内部究竟发生了什么?为了回答这一问题,科学家们构建了从宏观到微观、从经典到量子的各种模型,其中,伊辛模型脱颖而出。它不仅揭示了磁性起源的深层机制,更在此后的一个世纪中不断演化,跨越物理边界,成为计算数学、人工智能乃至社会科学的“隐形引擎”。本文将从伊辛模型的物理渊源出发,探索它如何走入组合优化问题的数学世界,并最终如何在多学科应用中焕发出意想不到的光芒。

一、从磁铁到模型:伊辛模型的物理渊源
伊辛模型源起于日常所见的磁铁,后来它却遭受争议不断甚至一度归寂于尘埃;所幸,是金子总会发光,伊辛模型最后乘着新世纪的大风重新掀起研究热潮,这又是怎么一回事呢?
1.1 电磁学时代
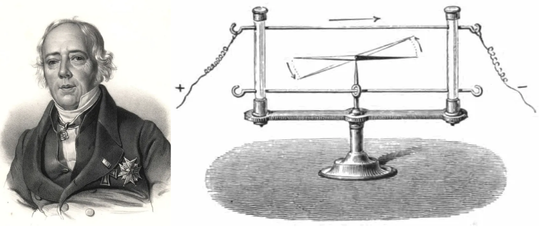
奥斯特和电磁偏转实验 (图片来源:网络)
关于磁铁和磁性的研究离不开电。1820年,丹麦物理学家奥斯特(Hans Christian Ørsted)在一次讲座中接通电源后竟然发现一旁的小磁针发现了偏转。这一发现使他欣喜不已,因为这一偶然出现的现象印证了此前的说法:不仅电可以生磁,磁也可以生电!这一发现揭开了电磁学的序幕,标志着电磁学时代的到来。

安培和分子电流假说 (图片来源:网络)
奥斯特将他的发现写成论文公布出来仅一个多月后,法国物理学家安培(André-Marie Ampère)就提出了分子电流假说对此进行了阐释,即认为构成物质的小分子可以像地球那样绕中轴自转,由于带有电荷,这就相当于是一圈电流——根据奥斯特电生磁的理论,应当能产生磁场;这样,物质实际上就由一个个小磁铁构成。这些小磁铁可以想象为我们平常玩的条形磁铁,也具有不同的两极,遵循同极相斥、异极相吸的原理。当外部没有磁场时,物质内部的小磁铁由于温度等其他因素的扰动变得杂乱无章,宏观总磁性相互抵消,所以物质表现为不具有磁性;而外部加上磁场时这些小磁铁就会在这种强有力的力场下调转方向,全部乖乖的沿着磁场方向排列从而使得物质在宏观上产生磁性。
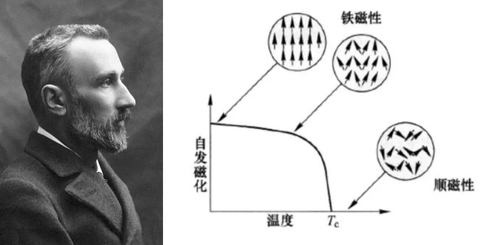
皮埃尔·居里和铁磁相变曲线(图片来源:网络)
后来,人们又在实验中发现磁性物质在其温度超过某些值后会“突然”失去磁性,这又是为什么呢?
1.2 铁磁性的微观本质
大家都知道著名的诺贝尔获得者,法国的物理学家居里夫人吧,正是她的丈夫皮埃尔·居里(Pierre Curie)于1895年研究发现,磁性物质存在一个“温度点”,只要物质所处环境的温度超过这个值就会使得物质失去磁性。不仅如此,在越过这个点之后物质所属的相区也会发生改变,一般会从铁磁性变为顺磁性。
这里解释一下什么是铁磁性和顺磁性,上面已经说物质可以在磁铁的作用下出现磁性,这个过程就叫“磁化”;磁化的过程会使内部小磁铁重组而产生一个宏观磁场;但是由于物质本身性质不同,磁场的方向与外加磁场方向不一定相同,我们据此把物质分为三类:顺磁性、铁磁性和抗磁性;前两种方向与外部相同而最后一种相反,但铁磁性最终产生的磁性要远大于顺磁性,并且在外部磁场撤去后仍能保留磁场。后来,为了纪念这位伟大的科学家,人们就把这个点(上图中的温度Tc)命名为“居里点”。
铁磁性所对应的微观本质应该是什么样的呢?1920年德国物理学家楞次(Wilhelm Lenz,注意不是发现楞次定律的那个俄国科学家)研究了这个问题并提出了一个理论模型:他认为可以把物质内部想象成一张网格,每个小格子里都分布有一个原子,这个原子用一个简化的箭头表示,箭头方向就代表着该小磁铁的磁场方向(上边提到的安培分子电流假说认为,每个原子都是一个个小磁铁),就像这样:

楞次的网格模型:不同颜色的箭头代表不同磁场方向的原子 (图片来源:网络)
1.3 伊辛模型的提出
后来,他的学生伊辛(Ernst Ising)在导师以上模型的基础上提出了一个简化模型,并得到一维物质无法保持磁性的观点:他的模型包括了两种磁性情况;主要是基于海森堡此前提出的有关自旋的模型而建构起来的(海森堡是量子力学有名的奠基人之一;这里提到的自旋起源于两个研究生的假设,后来被实验所证实,它是一种区别于常见坐标变量的新变量,就像质量一样,它也是微观粒子的内禀属性之一)。

恩斯特·伊辛 (图片来源:网络)
这个模型的物理图景是这样的:首先我们物质总是倾向于处在能量最低的状态(能量最小原理),而对铁磁系统来说,原子磁场指向方向相同时彼此之间的相互作用能量会比较小,因而原子之间的相互作用,也就是磁力会倾向于使它们保持同一指向;但温度等扰动却会破坏这一倾向,它倾向于使系统变得杂乱无章,这使得小磁铁们的指向最终很难保持一致,使得最终无法表现出宏观的磁性来。
这个模型就是著名的伊辛模型。
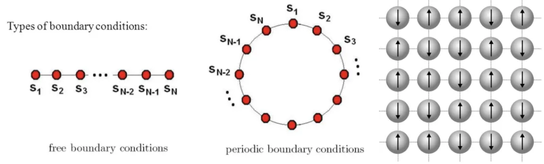
一维和二维伊辛模型(图片来源:网络)
1925 年 Ising 发表了一篇短文,作为他博士论文的总结。他精确地计算了自旋的一维晶格系统的配分函数。伊辛首先证明了在任何温度下都不会在一维上发生向铁磁有序状态的相变。
后来,楞次和伊辛经过简单的推导就认为,这个结论对二维和三维物质同样适用,即它们在任何温度下由于同样的原因均无法表现出磁性。这个模型乍听起来很高大上,考虑到伊辛模型是我们今天的主角,读者可能会认为它应是准确无误的。但是…
1.4 关于伊辛模型的争论
但是!
这个模型提出的背景是为了解决磁铁受热过程中关于其微观本质变化的细节问题;但伊辛模型此时似乎未能很好的回答这个问题——三维物质可以表现出磁性,也就是说,伊辛模型的简单外推并不符合铁磁性物质的实际情况。伊辛做了一维模型的求解,但不能简单的直接推广到二维、三维中去。由于涉及的数学过程太复杂,在当时还没有被完整的求解出来。
所以在当时这个模型确实引起了很多争议,以至于在伊辛模型被大量利用的今天,知道伊辛对该模型的贡献的人却寥寥无几。伊辛此后默默留在大学里承担教学任务,他再也没有回到科研中去。尽管争议很大,我们前面提到的海森堡却表明了自己独到的见解:他认为伊辛的成功之处在于:在自己导师所解决的一系列关于铁磁体细节问题的基础上,伊辛提出了两个相邻原子之间的相互作用并不足产生铁磁性的假设。
所以,铁磁性的产生可能还需要别的什么东西?某一种更强的力?相关问题的研究由于数学工具的缺乏而停止了脚步,渐渐的被岁月所遗忘…...
1.5 二维解的突破
这个问题再一次“上热搜”始于上世纪40年代理论物理学家昂萨格(Lars Onsager,1968年诺贝尔化学奖获得者)对该问题的重新关注。他把目光放在二维伊辛模型上,决心要以一种更加严谨的方法进行验证,或者证伪。

昂萨格 (图片来源:网络)
二维伊辛模型的复杂之处在于,此时对某一个箭头(也就是我们前面提到的原子磁场方向)来说,已不止像一维那样仅有左右相邻箭头的影响,还多了上下相邻箭头的影响,这大大增加了模型的解决难度。但大神就是大神,再难的问题也阻止不了昂萨格的脚步,他用一种鬼斧神工般的、至今也未能被完全理解的所谓“非人类”的数学过程证明了,二维伊辛模型的磁性会随着温度的改变而有所变化(而并非如伊辛所说在任何温度下都不会显现磁性),其在低温情况下温度对系统干扰度相对较小,此时原子之间的相互作用占优势——最终所有原子指向一致;当温度逐渐上升,天平会逐渐倾斜,到达某一个温度值时温度对系统的扰动将占优势,这时系统就不会表现出磁性。
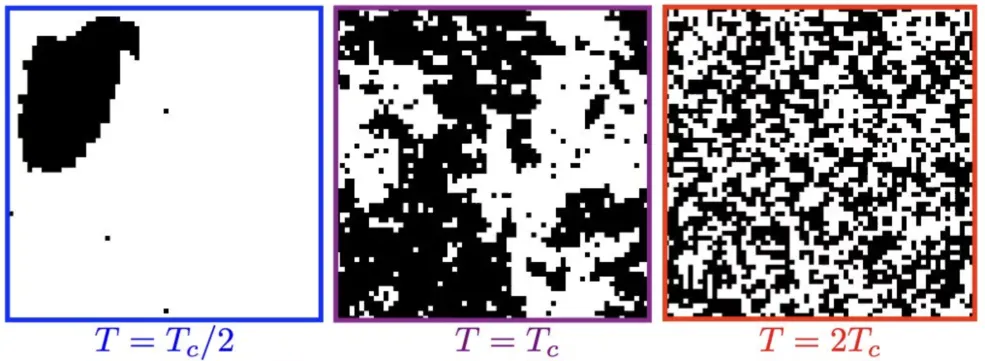
二维伊辛模型的磁性随温度的改变而变化(图片来源:网络)
其实这个结论乍一看与伊辛的导师楞次最初的猜想差不多;只是人家成功的把猜想用数学一步步推导出来了。这个结论表明,我们确实可以用一张二维网格去模型化实际物质,将一个个原子用箭头表示,而无需考虑粒子本身的各种纷繁复杂的属性。

杨振宁和昂萨格(图片来源:网络)
值得一提的是,在对伊辛模型求解所做的贡献中也不乏中国人的身影。
在凝聚态物理中存在各种各样的模型,这些模型并不对系统的具体细节属性有所规定,也就是说,对于两个包含原子不同的系统,当它们运用相同的模型进行计算(当然得满足该模型所规定的前提条件)时,所最终求解的边界条件、临界指数等值应当相等且与理论完全吻合(否则理论要被修正);二维伊辛模型中同样存在一组临界指数,对这些指数的求解一直是一个重大的研究课题之一:
杨振宁就曾于1952年严格求解出当时由昂萨格在一次国际会议上随手写下却未证明的一个指数;后来,1967年吴大峻等人又成功计算出另一指数。这组指数对标定物质相变具有关键作用。假如相变是一辆车,指数就是其上一个关键零部件;缺少此零部件,这辆车将无法开动。
自此,我们对伊辛模型的历史有了一个基本的了解。尽管伊辛模型的最初形式受限于一维推导,但随着二维解的突破,它逐渐展现出强大的数学结构。这也让人开始意识到,这一模型或许不止于物理,它的“形式之美”也许还隐藏着更广泛的应用潜力。
后来这个模型的应用范围从铁磁性研究拓展开来,被其他众多学科所应用而大放异彩,甚至在计算机领域、包括人工智能方向发挥自己独有的作用。接下来,我们将看到,这个原本为解释磁性的模型,如何“跨界”走进了数学与计算世界。
二、从物理走向数学:伊辛模型与组合优化的桥梁
首先我们可以思考这样一个问题,物理中与宏观具体可观可感的物理量有所对应的量,是如何与抽象的数学计算问题产生联系的?答案很简单,相似性。
我们在构建一个模型的时候,往往无法将所有因素纳入其中,我们只能先将这些因素抽象然后分类,接着根据它们之间的联系提出数学模型,最后我们还要把这个数学模型应用于具体的例子中看其能否准确预测结果;当然,模型一般需要在具体应用的过程经历多次不断的修改。
如果两个模型之间的元素可以相互对应,那么它们之间应该满足相同的数学法则,这是容易理解的。这就是建模从具体到抽象、再应用于具体的过程。虽然伊辛模型最初是为解释磁性而提出,但它本质上是一个抽象的最优化问题,这使得它天然地适用于更广泛的数学建模领域,特别是在组合优化问题中。
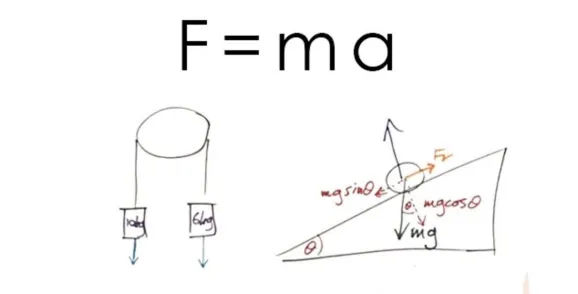
大家熟悉的最基本的建模案例(图片来源:网络)
2.1 提出问题
伊辛模型与组合优化问题就有相似之处。
什么是组合优化问题?我们将用组合优化问题中较为典型的“旅行商问题(TSP)”进行解释:首先我们已经知道几个城市(可以用点表示),以及每对(两个)城市之间的距离(它们是连通的,并且两点之间距离为直线,该直线长度是已知的);现在有一个商品推销员要从其中一个城市出发去其他城市,要求他要经过所有的城市,并最终回到出发地。
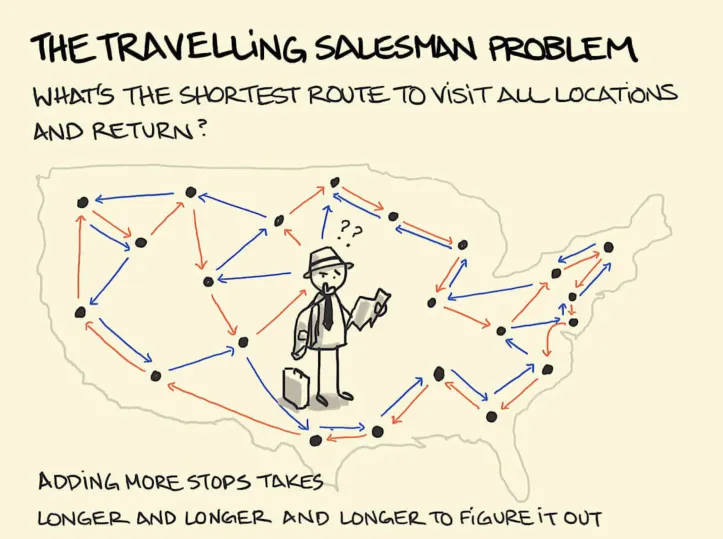
组合优化问题之“旅行商问题”(图片来源:网络)
不难理解,这个推销员所能选择的路径有很多,而假如我们是推销员,我们肯定希望能走那条路径最短,这样我们将能节省下更多的路费去完成同一目标。那么,这个问题应该怎么解决呢?部分读者可能会认为,可以通过列出并计算所有的路径,然后找到那个最小值就是我们的目标值;恭喜你,我们的数学家最初也是这么考虑的,这种方法被称为“穷举法”。
然而此方法却有一个致命的缺陷,那就是它将随着城市的增多增多再增多而变成一个“烫手山芋”——将最终到达计算能力的极限,就算是计算机也无能为力。
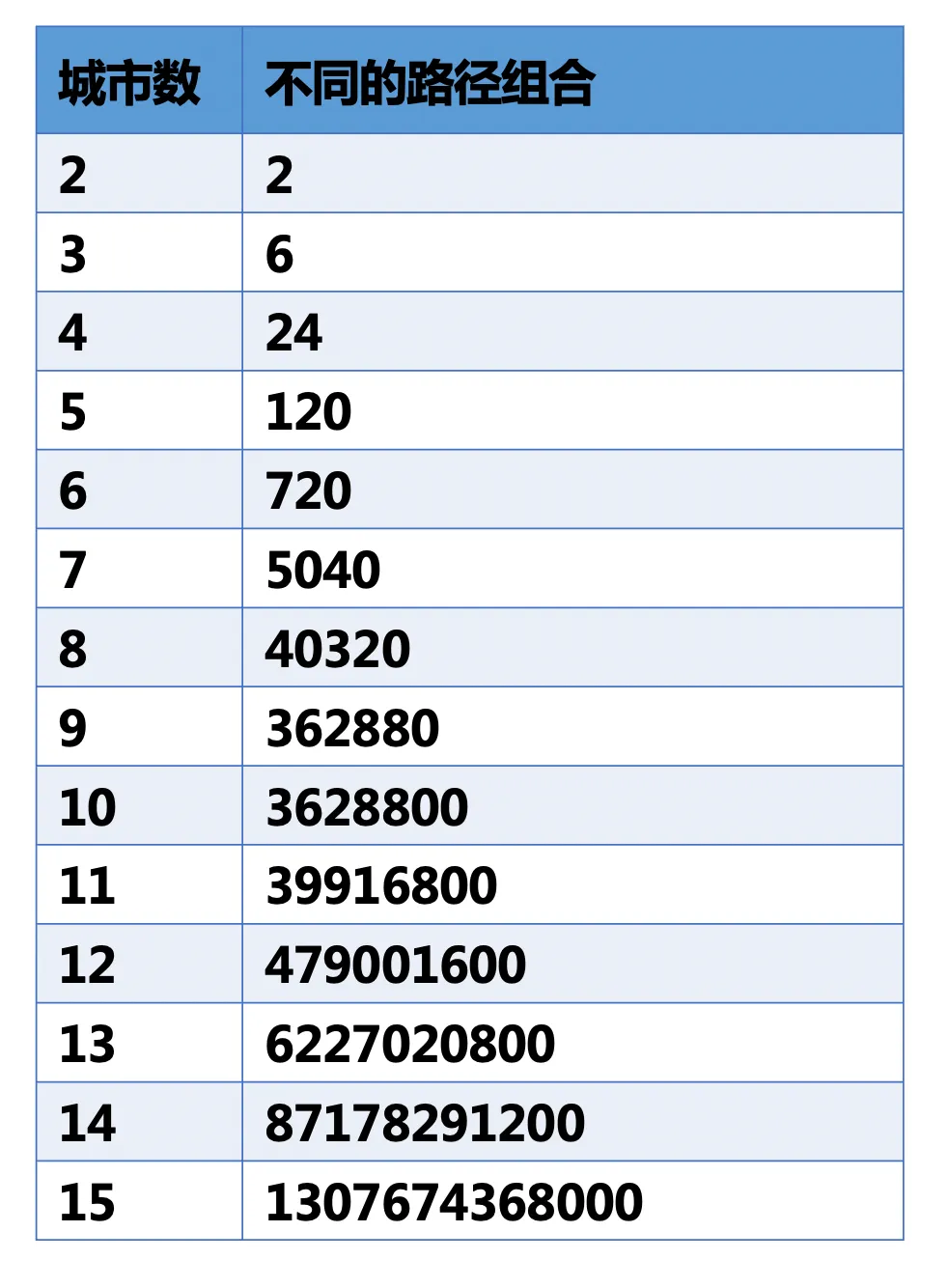
城市与路径组合数量
采用穷举法的时候,假设有n个城市,则需要执行n!次操作!举个例子,假设我们现在有10个节点(城市),我们将一共有9!=362880种可能性!它的计算时间数量级将为10!=1×2×3×4×5×6×7×8×9×10=3,628,800种可能性!
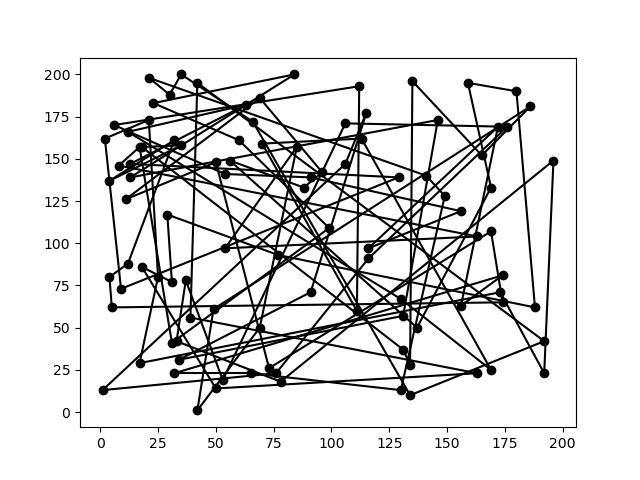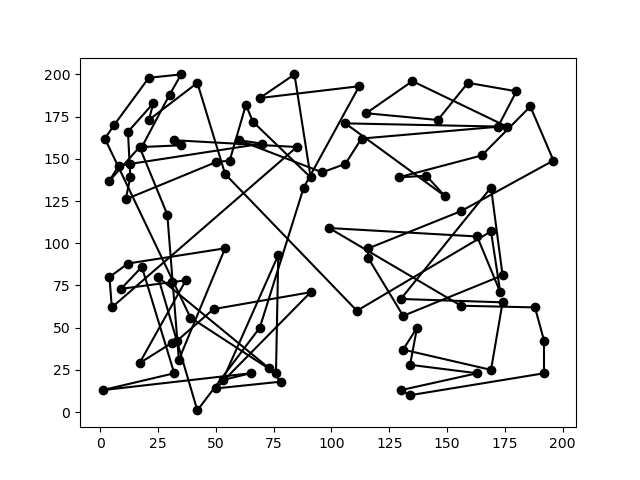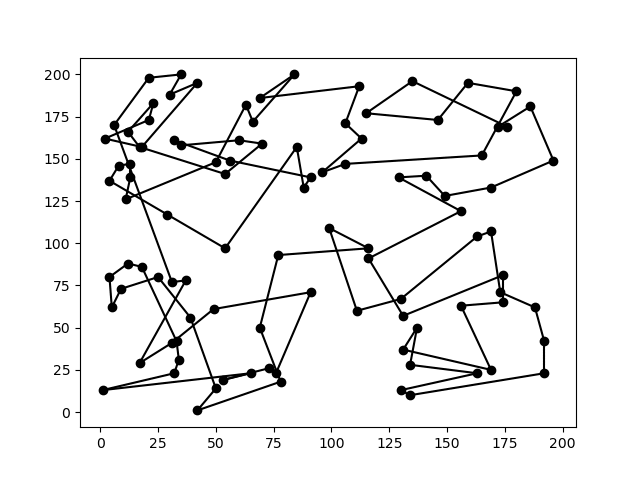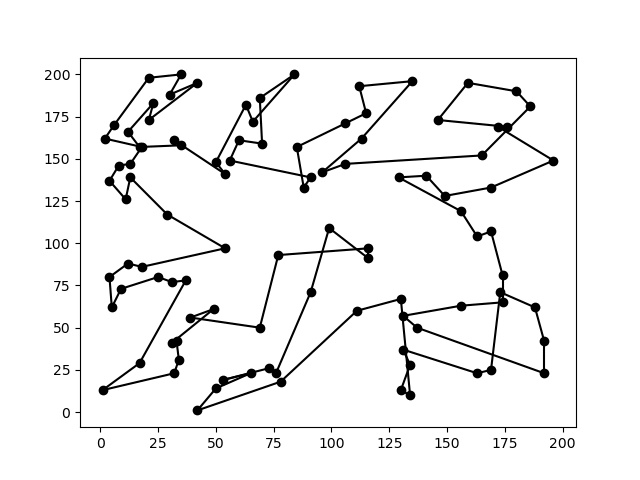
要找到几十个城市之间的最短路径,
可能需要超级计算机数万年的穷举(图片来源:网络)
现在大家应该明白什么是组合优化问题了吧?
就是在一组约束条件下,我们有多个可行解,而我们的目标是找到那个使目标函数(也就是“旅行商问题”的路费)最小的解。
2.2 模型对应
那么,这个问题如何与我们物理中的伊辛模型对应起来呢?我们可以这么考虑:
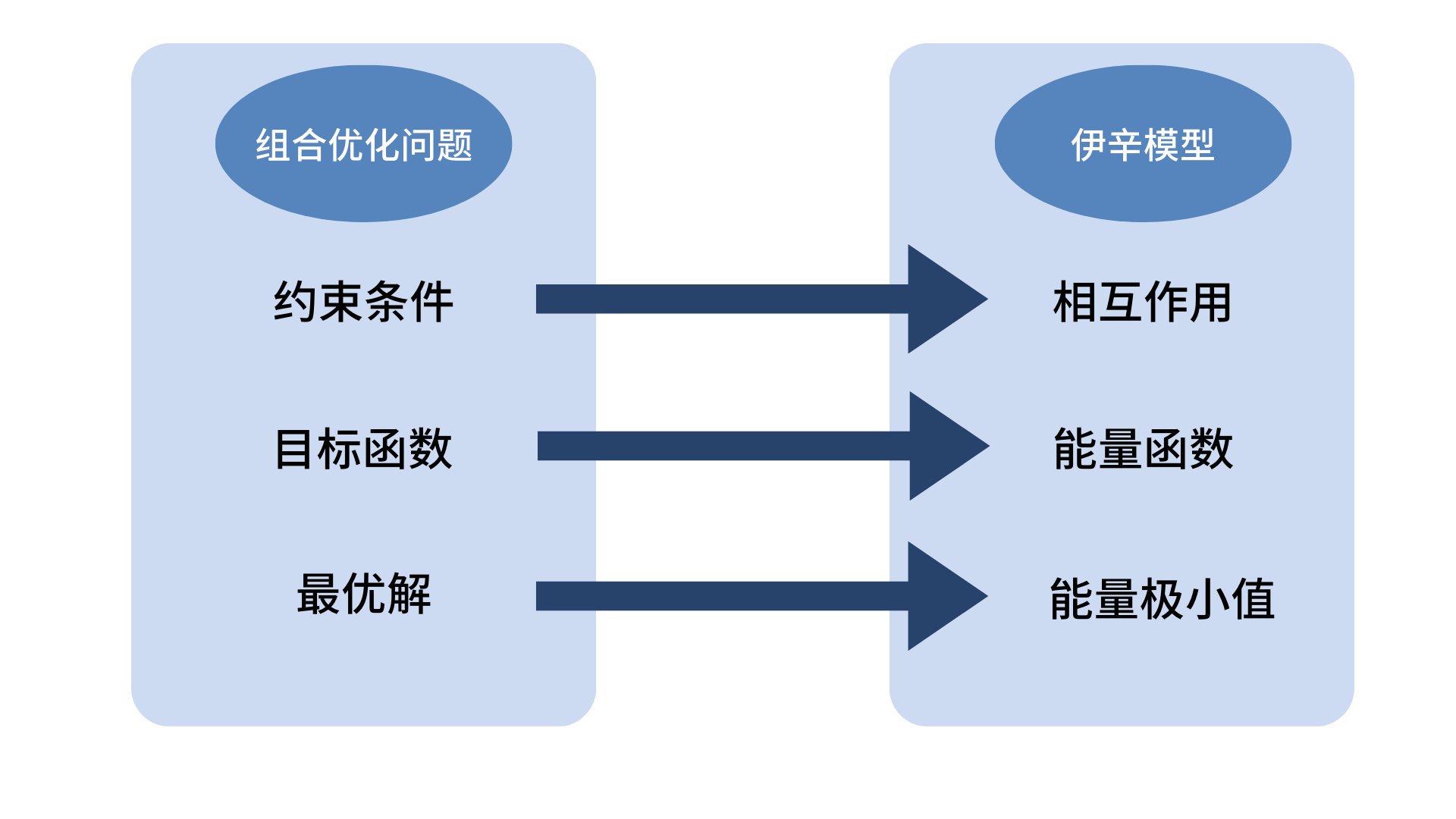
伊辛模型与组合优化问题的对应关系
2.3解决问题
现在对应关系清楚了,那么我们是如何具体解决的呢?
首先,我们考虑这样一个伊辛模型,它具有N个变量,也就是有N个网格。注意我们的伊辛模型中是允许每一个网格中的原子具有两种可能状态的,它的磁场方向可以向上也可以向下;因此每一个变量给都有两个可能取值。
接着,假设我们现在有A个约束条件,也就是说,有A种相互作用。
最后,我们可以定义一个能量函数,这个能量函数与所有与A个相互作用有关的变量集合有关。
我们最终的目标转化成了,求解伊辛模型中使得能量函数取最小值所对应的原子状态的取值状态。
上述解决方法听起来似乎很简单,不就是找到这种对应关系然后求解最小值就行了吗?事实远非如此。科学家们为了解决这个问题,前后提出了一些相关的假设,比如近似推理算法,以及各种具体数学推导过程中所作出的细节性的假设等,这些假设往往不容易得到.
通过变量映射、能量函数设定以及状态搜索机制的构建,伊辛模型为我们提供了处理NP难问题的一种可能框架。但它的价值远不止于理论求解,正如我们即将看到的,它还在实际问题中大放异彩。
三、从物理走向数学:伊辛模型与组合优化的桥梁
模型之所以伟大,往往不在于它原本解释了什么,而在于它最终“解释了多少”。伊辛模型的发展正印证了这一点——从物理启程,它在多个领域焕发出意想不到的生命力。
如果说上一章揭示了伊辛模型在数学上的广泛适用性,那么本章将带你看到它在实际问题中的“落地生根”。从物理计算到人工智能、从材料科学到社会决策,伊辛模型的结构之力令人惊叹。
3.1 解释磁场现象
前面我们说过安培假设物质磁场起源于其内部运动电荷产生的电流,但我们不禁要问,如果仅仅由内部电流产生磁场的机制,是否足以维持一个磁铁永久的磁性?
之所以提出这个问题是因为,自然界中存在一些永磁体,这些物质一旦被外磁场磁化后,即使脱离开此外磁场,也不会失去磁性;但是如果仅靠内部电流元的有序排列,显然不可能维持永久的磁性,这是因为假如离开外磁场,内部此前在外磁场作用下有序排列的电流元,极有可能在温度场的扰动下变得无序,从而使得磁铁失去磁性。
事实上,永磁体之所以能长久的保持磁性,是源于内部大量原子自身所带的属性造成的。这种原子本身自带的的禀性被称为自旋;我们可以不太准确的把这种自旋“理解为”是微观粒子像地球一样围绕地轴作自转。之所以不准确,是因为自旋属于微观属性,它实际上并不是微观粒子的自转,事实上我们无法在宏观世界中找到它的完美对应。原子的自旋能使自身产生一个固有磁矩,就一个小磁铁。
在外部磁场的干预下,物质内部的原子自旋磁性方向将会趋向于与外部磁场方向相同,于是众多的原子结合起来,在宏观上的表现就是具有磁性;而当外部磁场撤掉,这些原子的磁矩的方向并不会马上改变,而是会保持原来的方向,这样,宏观的磁性也就保持下来了。
但我们还要问,这些微观粒子它们怎么知道自己要向哪个方向旋转?
此时我们就可以应用伊辛模型来解决问题了。伊辛模型告诉我们,在高温环境下,原子自旋的指向由于热运动的干扰是随意的,随着系统逐步冷却并接近相变临界点,原子间的磁力相互作用使得某个原子周围的原子倾向于与它以相同的方向旋转、又以相同的机制影响其周围的原子……这样逐渐聚集起许多有序的原子群“岛屿”,并越长越大,在这些岛屿内部,所有自旋磁矩都指向同一方向。这就是宏观物体磁性的来源。可以用伊辛模型中的“临界指数”来以描述这一过程,例如最大的岛屿的是怎样生长的。

当 Ising 模型处于临界温度时,它包含各种尺寸的对齐内部自旋方向的“岛”。(图片来源:网络)
3.2 退火算法与蒙特卡洛算法
伊辛模型还可以被用于计算机领域而成为某些著名算法的基础,比如著名的退火算法,它就是蒙特卡洛方法与二维伊辛模型结合的产物。
退火算法,得名源于冶金行业的一个名词“退火”;在冶金行业中,为了减少材料(如钢材等)缺陷、增大材料颗粒粒径,往往将材料先加热然后以一定速率慢慢冷却。未经退火处理时,钢材中的晶体颗粒会停留材料的局部晶体能量最低的位置,在加热后,这些颗粒就可能获得足够的能量去逃离原来的局部能量最小的位置,并在缓慢的冷却过程中,重新找到更大范围内能量最低的位置“安顿”下来,这样,整体材料的能量就有可能进一步降低,也就是调整了钢材内部的晶体组织,消除组织缺陷。
那算法上的“退火”又是怎么一回事呢?要理解这个概念,首先先认识一下蒙特卡洛方法。
蒙特卡洛方法得名于著名的“赌城”蒙特卡洛,这一计算方法的本质可以比喻成随机的“掷骰子”——从整体中去随机抽取出一些部分作为样本,接着利用这些大小有限的样本内容进行一些统计学量的计算,最后利用此结果估计出整体的统计学量,依托着计算机强大的运行能力将数值计算推向了实用化。如下图所示:
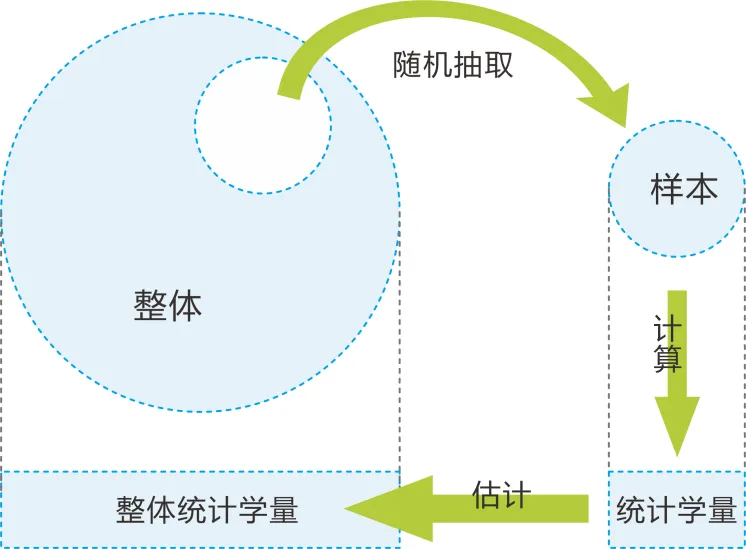
蒙特卡洛计算方法
我们把从整体部分抽取出样本的操作称为抽样。抽样一共有两种方法,即简单抽样法和重要性抽样法。
这两种方法都是根据其抽样的具体操作而命名的:其中,简单抽样正如其名一样,指的是从整体中均匀随机抽样,即随机的从整体中抽取样本,比如在某个特定十字路口附近采访路人。
而重要性抽样法则是根据对象的重要性程度来决定抽取多少;比如对一个文科班来说,可能女生的数量要远远大于男生——假设女生与男生数量比为5:1。这时候假设我们要调查某一款游戏的受欢迎程度而在该班中分发调查问卷,如果我们仍然选择简单抽样法,那很显然这样做所得到的结果是很不准确的,因为明显女生数要远大于男生数,这样我们所可能得到的结果大抵是此游戏不受欢迎。
这时,重要性抽样法登场了;这种方法是这样的,首先将整体分类,接着根据这些类的大小在整体中所占的比重来决定要从中抽取多大的内容进入最终的样本。显然,对上面所举的例子我们应当用重要性抽样法进行抽样。
一个运用蒙特卡洛法的例子就是用撒点的方法求得某不规则二维平面的面积。现在假设给定一个不规则二维平面,要求求出其面积S0,我们可以这么考虑:首先我们在此不规则二维平面周围画上一个规则的、我们可以轻易求出其面积S的二维平面,比如说一个正方形;接着我们向这个正方形撒点(硬币、骰子都可以,甚至花生也行,但一定要保证它们大小相近),假设一共撒了N个点;观察有几个点落在此不规则平面内,记为N0。
则S0≈(N0/N)S,如下图所示:
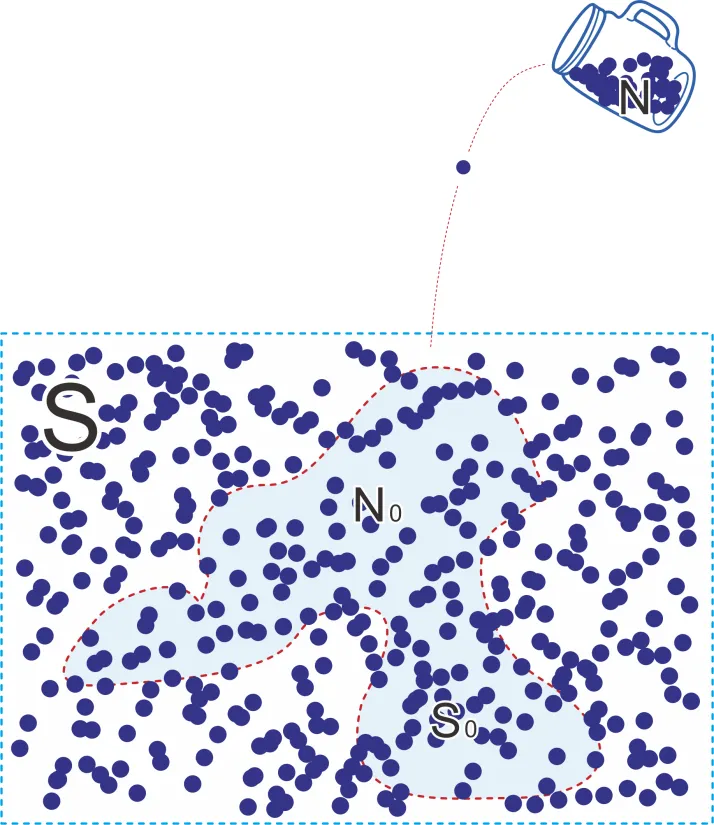
图3:撒点法
利用同样的方法,我们甚至可以求出相当精确的π值。
那么,蒙特卡洛方法如何与我们的二维伊辛模型进行结合呢?根据此前我们对伊辛模型的介绍我们知道,伊辛模型在一、二、三维都具有相应的图像,分别对应着链、正方形和正方体。其中,一维伊辛模型具有严格解;二维伊辛模型的严格解很难被理解;三维伊辛模型的严格解则仍是未解之谜。
随着计算机技术的发展,科学家将难以理解的二维伊辛模型的严格解交给计算机处理,将其与蒙特卡洛方法结合之后就是模拟退火算法。模拟退火算法的计算步骤可以归纳如下:首先我们在体系中随机的选定一个原子,然后看它是否翻转,假如它翻转我们就去计算翻转前后体系的能量差,然后我们会有一个评价函数(这个评价函数由具体研究的体系而决定,而且它往往是进行这种算法的核心所在),根据这个评价函数我们将可以判断最初随机选择的那个原子是否可以翻转:如果可以,继续选定一个随机原子、重复以上步骤;如果不行,则回到第一步重新选定一个随机原子。
这个算法与伊辛模型的联系之处在于,它借用了二维伊辛模型网格状的结构进行问题的考虑,并且其中“原子的翻转”就对应着二维伊辛模型中一格点原子的两种自旋状态;另外,我们知道,二维伊辛模型只考虑近邻的作用,所以此时体系能量的改变会与此随机原子周围四个原子的自旋状态有关(它们的自旋状态联系着它们所具有的能量)。事实上,体系能量的改变往往是最近邻四个原子能量改变值总和的四倍。
3.3 社会学问题应用
你大概不会想到,物理学领域的伊辛模型也能用于社会学问题的研究中。我们举一个例子。
比如欧美地区现有一个地区要进行选票,每个选民可以选择支持或反对,这就对应着伊辛模型中的两种可能的自旋状态;而这些选民的态度会受到环境的影响而发生变化,比如某个选民本来决定投支持票,但是他于当天看到某个新闻或者听说其他选民的观点,可能临时决定投反对票,这就对应着伊辛模型中温度对系统的影响;
最后,选民之间的关系就对应于伊辛模型中格点之间自旋的相互作用,而对每一个选民来说,更可能影响到他最终所投选票的更可能是他的邻居而不会是住的离他很远的人,这样就完全与伊辛模型中采取的只计入最近邻相互作用相对应。这样,就能利用伊辛模型对选票及选民的趋势问题进行计算和预测了。
这组对应关系如下图所示。
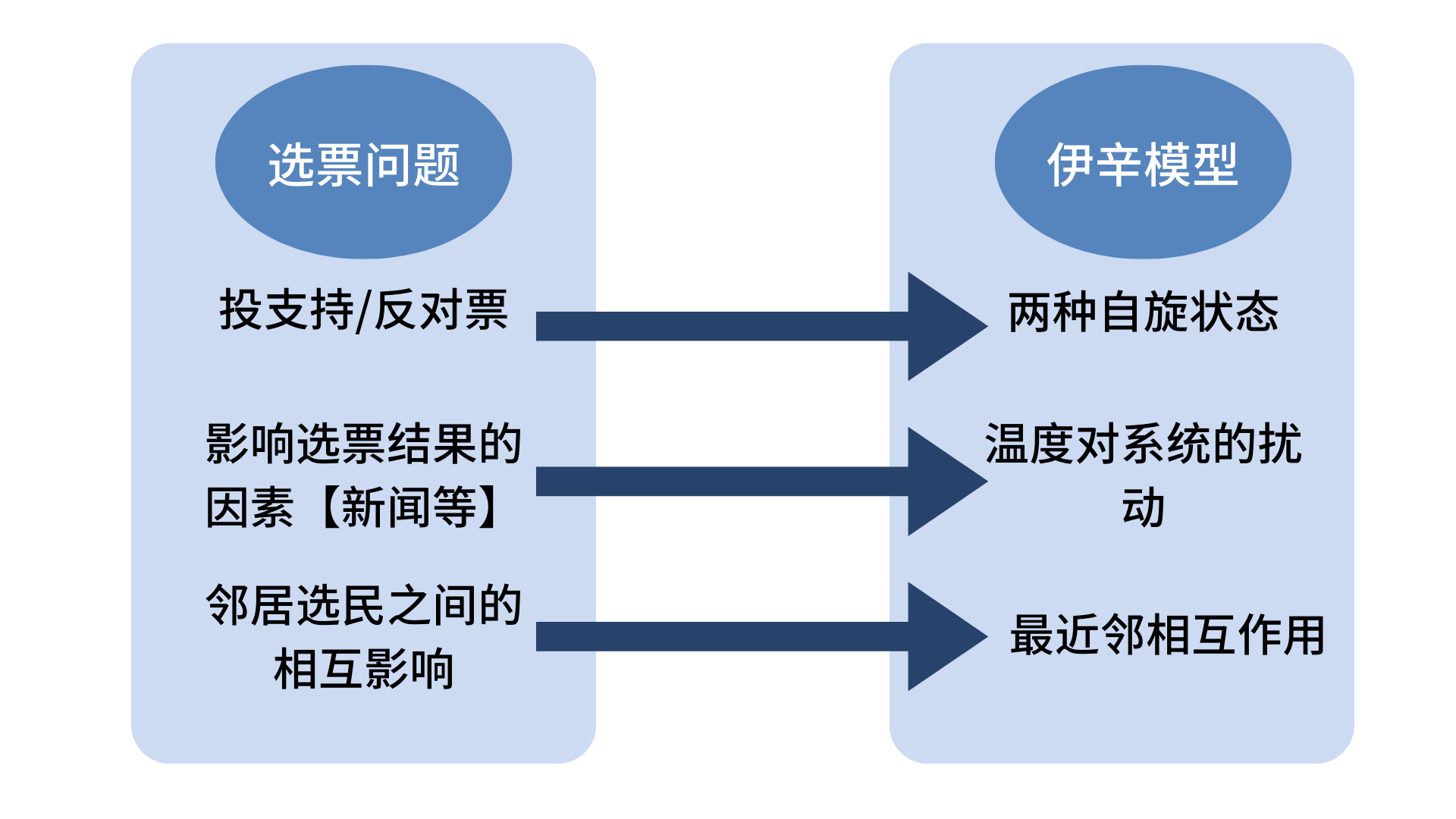
四、总结
伊辛模型的魅力,从不局限于它对磁性现象的解释。作为一种简洁却深刻的系统模型,它为我们提供了一种观察“局部决定整体、简单蕴含复杂”的思维方式。从一维的无磁性结论到二维的相变证明,再到模拟退火、选票预测等应用,伊辛模型的跨学科价值早已超越了最初的物理框架。它的旅程是一种科学模型如何在不同领域“破圈而出”的真实写照,也提醒我们:在这个高度复杂的世界中,洞见常常藏在最简单的结构之中。
| 








