本帖最后由 薛定谔了么 于 2025-8-7 22:46 编辑
深度学习算法虽在监督学习领域取得显著进展,但无监督学习中多数模型的计算复杂性仍是一大挑战。而量子计算的发展为加速机器学习任务带来了希望,量子处理器在优化和采样方面的能力,让研究者开始探索量子机器学习这一新兴领域。
在这一背景下,变分自编码器(VAEs)作为强大的生成模型,虽能有效进行推理,但经典模型在表示复杂数据分布时存在局限。于是,将量子计算与VAE结合的想法应运而生,量子变分自编码器(QVAE)便是这一探索的成果。
二、QVAE 的突破与创新
该论文的核心贡献在于首次将量子玻尔兹曼机(QBM)引入变分自编码器的潜在空间,构建了端到端可训练的量子生成模型,具体创新点如下:
提出量子变分自编码器(QVAE)架构:QVAE 将经典 VAE 的潜在生成过程替换为量子玻尔兹曼机(QBM),利用量子效应(如量子叠加、横向场)增强潜在空间对复杂数据分布的表示能力。与此前的 QAHM 不同,QVAE 保留了 VAE 高效的 “编码器 - 解码器” 结构,同时通过量子机制拓展了模型的表达边界。
定义可端到端训练的量子损失函数:论文推导出 “量子下界(Q-ELBO)” 作为训练目标,这一损失函数是对数似然变分近似的量子版本,解决了量子模型训练中梯度难以传播的问题。通过最大化 Q-ELBO,QVAE 可像经典 VAE 一样通过反向传播实现端到端训练,无需依赖复杂的 “唤醒 - 睡眠” 等非端到端算法。
验证量子效应下的有效训练能力:论文通过量子蒙特卡洛(QMC)模拟(如连续时间量子蒙特卡洛 CT-QMC)训练 QVAE,证明即使在量子效应显著的场景(如横向场非零),模型仍能有效学习。这打破了 “量子效应会干扰模型训练” 的担忧,为量子生成模型的实用化奠定了基础。
在标准数据集上实现领先性能:基于离散潜在空间的经典 VAE(DVAE)在 MNIST 数据集上,通过 RBM 作为潜在空间,实现了当时离散变量生成模型的最优性能(如 256×256 RBM 的对数似然达 - 83.5)。而 QVAE 在引入量子效应后,性能仍与经典模型相当,证明了量子模型的竞争力。
三、从经典 VAE 到 QVAE 的演进路径
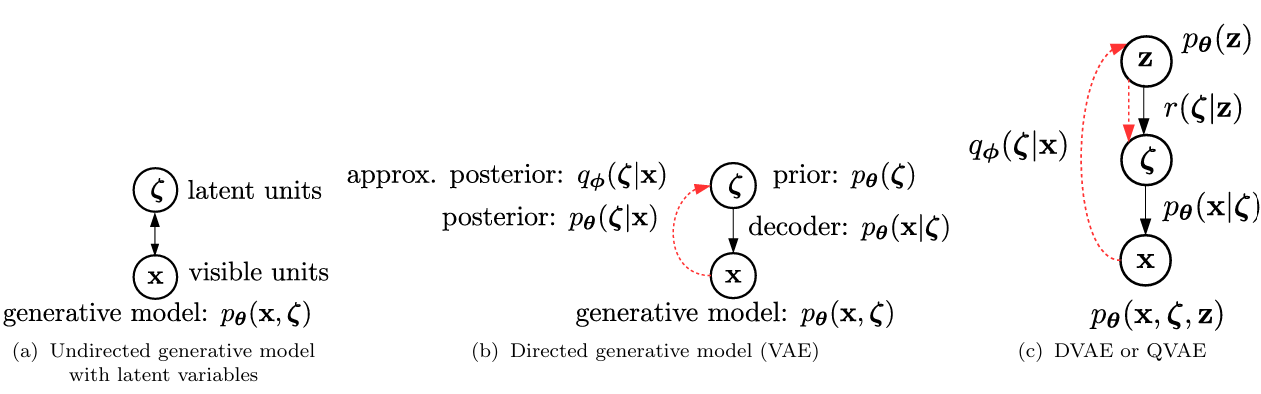
图1 生成模型结构对比图
1. 经典变分自编码器(VAE)基础
VAE通过引入可处理的变分近似分布qϕ(ζ|x)来逼近真实后验分布pθ(ζ|x),并通过最大化证据下界(ELBO)来优化模型,公式如下:
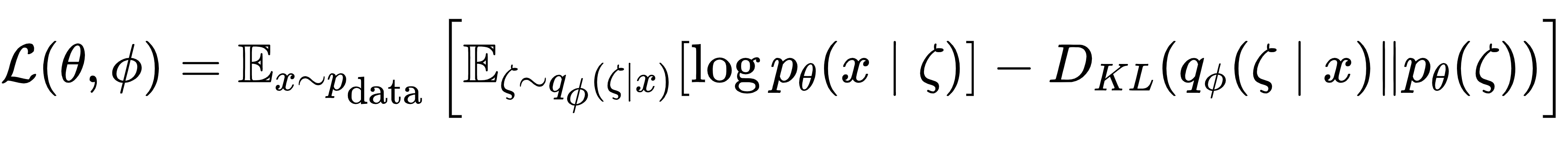
其中,第一项为重建项,要求从潜在变量还原输入数据;第二项为KL散度项,使近似后验与先验分布接近。
2. 离散潜在空间的VAE(DVAE)
为处理离散潜在变量,DVAE引入辅助连续变量,通过平滑概率分布实现重参数化技巧,解决离散变量梯度传播问题。同时,使用限制玻尔兹曼机(RBM)定义先验分布pθ(z):
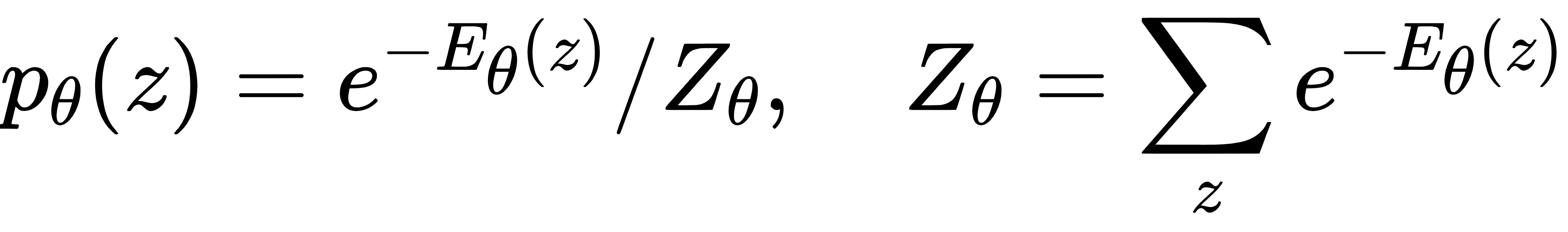
其中Eθ(z)为能量函数,包含偏置和权重参数,能捕捉潜在变量间的复杂关联。
3. 量子变分自编码器(QVAE)
QVAE用QBM替代RBM作为潜在空间的先验。QBM的哈密顿量为:
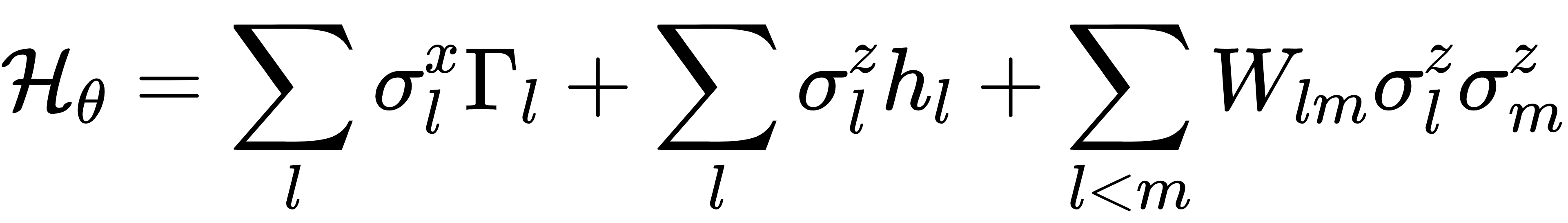
其中包含泡利算子和横向场等量子特性,使其能表示更丰富的分布。QBM的概率分布为:
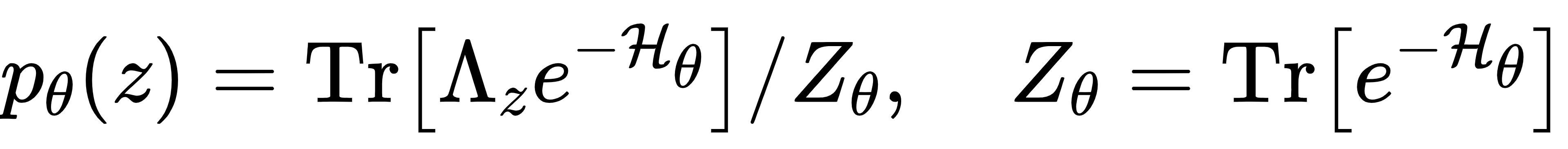
由于量子分布计算复杂,QVAE使用量子下界(Q-ELBO)进行训练,保证了训练的可行性。
四、实验验证
论文在 MNIST 数据集(静态二值化处理)上进行了系统实验,结果如下:
1. 经典 DVAE 的性能领先性

图2 DVAE 生成与重建 MNIST 数字效果图
DVAE 随 RBM 规模增大,性能持续提升:
32×32 RBM:ELBO=-99.3±0.2,对数似然 LL=-90.8±0.2;
256×256 RBM:ELBO=-89.2,LL=-83.5。
表1 不同离散变量变分生成模型性能对比表
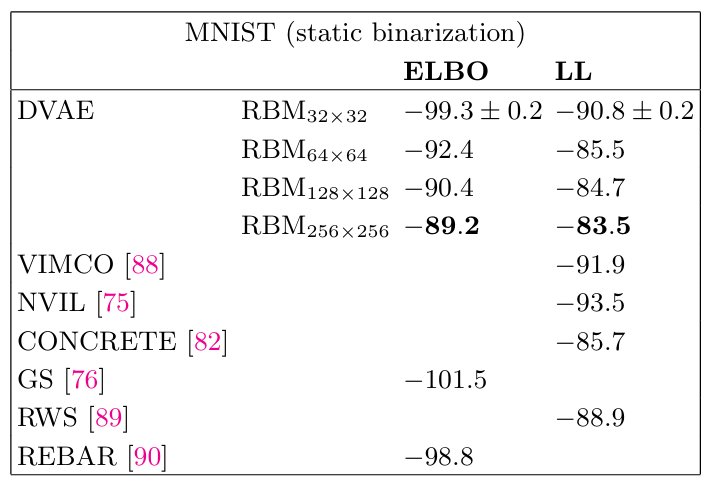
对比其他离散变量模型(如 VIMCO 的 LL=-91.9、CONCRETE 的 LL=-85.7),DVAE 凭借 RBM 对变量关联的捕捉能力,成为当时性能最优的离散潜在变量生成模型。
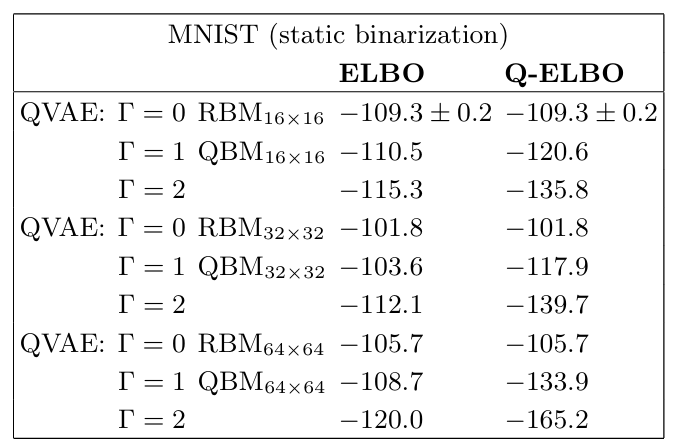
2. QVAE 在量子效应下的稳定性QVAE 在不同横向场(Γ)下的表现显示:
当Γ=0(QBM 退化为 RBM),16×16 QVAE 的 ELBO=-109.3±0.2,与经典模型一致;
当Γ=1(量子效应较弱),ELBO=-110.5,略低于经典情况,但生成样本质量仍良好;
当Γ=2(量子效应显著),ELBO=-115.3,虽性能下降,但仍能生成可识别的 MNIST 数字。
表2 QVAE 不同参数下的 ELBO 和 Q - ELBO 值对比表
五、结论与展望
该论文通过构建 QVAE,成功将量子玻尔兹曼机融入变分自编码器,证明了量子计算在生成模型中的应用潜力。QVAE 不仅在 MNIST 上实现了与经典模型相当的性能,更通过量子下界解决了量子模型的训练难题,为后续研究奠定了基础。
尽管当前受限于量子蒙特卡洛模拟的计算成本,QVAE 的潜在单元数量较小(最大为 64×64),但论文指出,量子退火器可加速 QBM 的采样过程,有望突破这一限制。未来,随着量子硬件的发展,QVAE 或将在图像生成、药物设计等领域展现出超越经典模型的优势,成为量子机器学习实用化的重要突破口。
论文链接:Quantum variational autoencoder - IOPscience | 








