本帖最后由 RangerQ 于 2025-8-23 13:30 编辑
文章概要: 本文针对高价值支付系统(HVPS)流动性占用高、结算顺序优化难度大等问题,提出一种基于混合量子退火的支付顺序优化算法。该方法将优化问题转化为QUBO模型,并在D-wave 混合量子求解器上运行。通过在支付进入系统前集中重排队列的方法,在不显著增加结算延迟的前提下显著降低所需流动性。实验基于加拿大HVPS的真实交易数据,平均每日节约流动性约2.4亿加元,个别日节约超过10亿加元,并证明量子算法在70笔/批规模下仅增加90秒延迟,显示出量子计算在金融基础设施优化中的可行性与潜在经济价值。
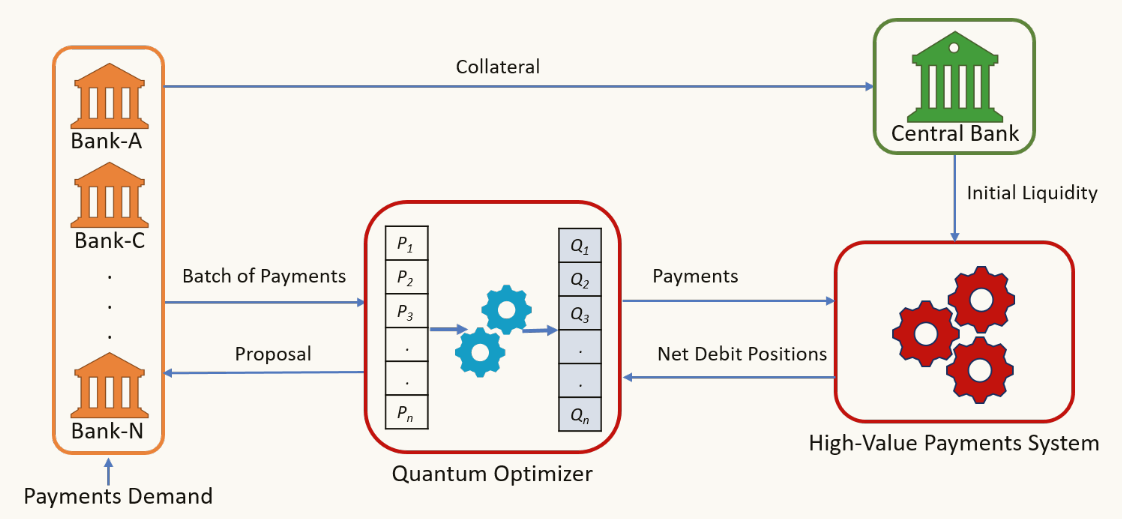
一、背景介绍
1.高价值支付系统
高价值支付系统(High-Value Payment Systems,HVPS)是国家级金融市场基础设施的重要组成部分,用于处理金融机构之间金额巨大、时间敏感的资金转移,包括银行间结算、大额企业支付、证券交易清算、外汇交易结算等关键业务。它通常由中央银行运营或监管,是维护金融稳定的重要枢纽。
多数国家的 HVPS 采用**实时全额结算**(Real-Time Gross Settlement,RTGS)模式:
- 实时:支付指令一旦满足条件即刻处理;
- 全额:每笔支付独立结算,不进行抵消;
- 不可逆:结算完成后不可撤销,确保资金安全与最终性。
以加拿大 Lynx 系统为例,其每日处理的支付总额可达全国 GDP 的数倍,参与机构需在交易前向央行提供 150–200 亿加元流动性作为结算准备。这种模式虽能保障安全与确定性,但流动性消耗巨大,参与者往往延迟发起支付以等待入账资金,形成流动性—延迟权衡,甚至可能引发“支付堵塞”。提升 HVPS 流动性效率通常有两条路径:
1. 改变提交行为:通过激励或规则引导参与者协调支付时间;
2. 调整结算顺序:在支付进入系统后,改变处理顺序以降低峰值流动性占用。
本论文选择第二条路径,结算顺序优化是一个NP-hard 组合优化问题:
- 假设有n笔待处理支付,每种可能的结算顺序是一种排列,总共有n! 种可能;
- 要在这些排列中找到最小化系统总流动性需求的顺序,就必须在巨大的排列空间中搜索;
- 随着n增长,计算量呈阶乘级爆炸,类似旅行商问题(TSP),经典算法在可接受时间内难以求得最优解。
2.量子模拟退火与QUBO建模
近年来,量子计算在组合优化问题中展现出潜力,尤其是量子退火(Quantum Annealing)技术,利用量子叠加、纠缠和隧穿效应在庞大的状态空间中搜索近最优解,能够在某些问题上优于纯经典算法。为了让问题能在量子退火器上运行,需要将其转化为二次无约束二进制优化模型(Quadratic Unconstrained Binary Optimization, QUBO),通过构建哈密顿量使其最低能量态对应于最优支付顺序。 文中提出了一种新型混合量子退火优化算法,其可作为集中式预处理器嵌入现有HVPS而不改变其风险管理框。该方法不仅对央行和金融机构具有直接参考意义,也为将量子计算引入支付、清算、证券结算等其他金融基础设施提供了范例。
二、建模思路:从支付队列优化到QUBO表达
1. 问题目标与变量定义
该问题的目标是在已知一批待结算支付指令的情况下,找到一种结算顺序,使系统在处理这些支付时所需的总流动性最小,同时确保在任意时刻没有参与者出现负的流动性余额。
定义以下关键变量:

2.优化目标
本问题的目标是最小化所有参与者在该批次结算后所需新增的流动性总额,即:

其中 b_α 表示参与者 α 为完成该批次结算所需增加的流动性,这相当于批次结算后最大净借方头寸的增加值。
3. 主要约束条件
1. 余额非负约束(防止透支): 对于每个参与者,在批次中任一结算步骤 t,结算后的余额必须大于等于零:

其中 f(α,i) 为返回交易 i 对参与者 α 的金额变化:收款为+v(v为付款金额),付款为-v,否则为0.
2. 位置唯一性约束(每个支付只能出现在一个位置):

3. 位置填充约束(每个位置只能安排一个支付):

可以发现约束2和3与旅行商(TSP)问题中“每个城市只能被到达/离开一次”的约束类似。
4. 转化为QUBO形式
QUBO模型要求目标函数为仅包含二进制变量的二次多项式,且不显式包含约束条件(约束需转化为惩罚项加入目标函数)。将该问题转化为 QUBO 的步骤如下:
1.引入惩罚项处理约束
- 对余额非负约束,引入惩罚参数 λ_1,将违反约束的情况平方后累加到目标函数中:

其中 s_α(t)≥0 为松弛变量,用于将不等式约束转化为等式约束,编码成二进制即可转化为QUBO变量。
- 对位置唯一性和位置填充约束,引入惩罚参数 λ_2:

2.得到QUBO哈密顿量
将以上优化目标和约束条件结合,得到最终的目标函数(量子退火的哈密顿量)为:

3. 二进制化与展开
所有变量 x_{i,t}、b_α(经过离散化)、s_α(t) 都转化为二进制形式,其中流动性增量 b_α 为货币金额,是非负连续值,需要进行离散化。例如,假设允许精度为 0.1 百万加元,且最大增量不超过 12.7 百万加元,则用 7 位二进制(2^7-1=127)即可覆盖范围:

其中 q_{α,k}是二进制变量,Δ 为允许精度,此处即取 Δ=0.1百万加元。
将哈密顿量中的平方项展开即可得到仅含二进制变量及其乘积的二次多项式,即标准QUBO形式。
以上转化具有下面几个优势:
- 物理可实现性:QUBO 是量子退火硬件(论文中的 D-Wave)的原生输入格式,构造的哈密顿量最低能量态与最优支付顺序一一对应;
- 约束内化:将约束转为惩罚项嵌入目标函数,使问题变为“无约束”形式,可直接在QPU上求解;
- 可扩展性:相同的QUBO框架可兼容不同HVPS的规则,只需调整约束函数 f(α, i) 与参数即可。
5. 将 CQM求解器的结果转化为最终的支付队列顺序
1. CQM输出形式
- D-Wave 的CQM求解器返回的是满足约束的变量赋值,包括二进制变量 x_{i,t} 的取值,以及其他辅助变量(流动性变量 b_α、松弛变量等)。
- 这些解中可能包含多个具有相同最优值或近似最优值的方案。
2. 从解到支付顺序的映射
- 根据 x_{i,t} = 1 的位置,将支付 i 放入最终的优化队列的第 t 位。
- 需要遍历所有支付和位置组合,重建一个按顺序排列的列表,作为新队列。
3.多解处理
- 如果有多个等价最优解,按业务规则选择,保留与原始队列最接近的方案或者根据支付金额/参与者优先级二次优化选择。
4. 可行性验证
- 虽然CQM已经考虑约束,但结果仍需在经典计算环境中逐笔模拟支付执行过程,确保:
a. 所有参与者在任意时刻余额 ≥ 0;
b. 批次结算时间在允许范围内;
c. 流动性节约确实达标。
5. 输出给系统执行
- 通过验证的队列顺序可以作为批次的优化结果输出,进入 HVPS 实际执行阶段。

三、数值求解结果
1. 数据来源与处理
实验使用 加拿大高价值支付系统(Lynx) 的真实交易记录,涵盖 30 个工作日,总计约 60 万笔支付,总金额达数万亿加元。这些数据具有强烈的日内周期性:早高峰(8:00–9:00)交易密集,大额支付分布相对均匀但在某些时段集中度更高,这种不均衡性正是流动性压力的主要来源。每次记录包含支付发起时间(精确到秒)、付款方与收款方的唯一标识、交易金额。为方便批量优化,预处理包括:
- 批次划分:将交易流按时间切分为固定大小批次,模拟实时流入队列的情境;
- 余额初始化:根据批次前的历史交易,计算每个参与者的初始净头寸和已累计的最大净借方头寸;
- QUBO 输入构建:根据批次交易构造目标函数与惩罚项,生成QUBO系数矩阵。
2. 计算平台与求解流程
使用 D-Wave 混合量子退火求解器(Hybrid CQM Solver),该平台结合量子退火器(QPU)与经典启发式算法,支持上千变量规模的QUBO求解。每个批次的求解流程:
- 构建 QUBO:将目标和约束二进制化、离散化后生成QUBO矩阵;
- 提交求解:QUBO 输入到混合求解器,执行量子—经典迭代优化;
- 解码与验证:从 x_{i,t} 恢复支付顺序,在经典模拟中验证可行性;
- 整合批次:将优化后的批次顺序拼接为全日的最终支付序列。
3. 实验结果
(a) 流动性节约
- 平均每日节约流动性 2.4 亿加元,个别日节约超 10 亿加元;
- 流动性节约比例最高可达原需求的 25%,显著降低了参与者的资金占用成本。
(b) 计算性能与延迟
- 单批次优化平均耗时 30–60 秒;
- 全日优化后平均增加约 90 秒 的结算延迟,远低于金融系统可接受阈值。
(c) 公平性与分布影响
- 节约效果在不同参与者间分布较均衡,未出现集中在少数银行的现象;
- 小规模批次优化在保持高节约率的同时,延迟增加最小。

四、分析与讨论
4.1 计算时间
利用量子优化器对队列重新排序包含以下步骤:
1. 按支付到达顺序累积一批支付;
2. 构建第第三节中描述的CQM对象;
3. 将对象发送至D-Wave系统的混合CQM求解器进行优化;
4. 对求解器输出进行后处理,提取解。

其中,支付队列优化的计算时间由两部分构成:
1. 批次积累等待时间(TwaitTwait): 与批量大小 n 呈线性关系;
2. 量子优化处理时间(TprocessTprocess): 受CQM模型复杂度驱动,呈立方级增长。


与SCIP经典求解器相比,经典求解器求解该问题时通常需2小时以上,且有时24小时仍无法解出。这表明经典求解器不适合实时应用,本问题更适合用D-Wave的混合量子–经典求解器。
4.2 求解质量
使用包含700笔支付的一个代表性数据集,下图展示了单一队列中前 n 笔支付(n 从70到700)情况下,批次大小与聚合最大净借方头寸的关系(黑色点)。图中还给出了与FIFO队列排列的对比(蓝色线),以及 CQM 求解器返回的可行解数量(红色柱状图)。

当批次大小不超过300时,CQM求解器的结果优于FIFO;然而,随着批次大小继续增加,结果开始劣于FIFO。这一结果质量下降与可行解数量的急剧减少相对应。对于批次大小超过 250 的情况,CQM 求解器基于 CQM 输入的多种属性自动选择的默认计算时间参数已不足以获得任何可行解,需要手动调整。对于批次大小为700的数据点,手动设置了3小时的混合量子计算时间,最终得到了优于FIFO的解。这些结果表明,当前的混合经典–量子退火技术在合理时间内可解决的最大问题规模约为 n ≲ 200。不过随着技术的不断发展和扩展,未来将拥有更多纠缠量子比特、可搜索更大状态空间的混合求解器,量子退火也能够处理更大的队列。
4.3 整体性能
将每天的交易分成批次,并使用批次大小 n = 70在 CQM 混合求解器上进行优化,然后与 FIFO(先入先出)进行对比。分析分为两种情景:
1. 情景一:
- FIFO 与 CQM 从相同初始条件(如 8:00 时的 mNDP)开始运行;
- 每批次的支付顺序固定(FIFO原顺序和CQM优化顺序各自独立进行整日结算);
- 最终在 18:00 时比较两者的日终mNDP。
2. 情景二:
- 逐批进行“赛马”比较:每个批次用FIFO和CQM各自运行一次,取表现更优的结果;
- 统计改进的批次数量、平均节省、中位节省、最大节省,以及是否有批次劣化。
在全样本分析中,批次大小为70时,量子优化器相较FIFO在日终可实现平均约2.399 亿加元的流动性节省,中位数为1.288 亿,节省分布呈指数型,最高单日节省达 12.64 亿加元;在9717个批次中,约一半无可优化空间,25.3% 经优化实现节省,其余因结构限制无法改善,可优化批次的平均、 中位和最大单批节省分别为1325万、79万和 3.3941亿,最大单批节省达12.89亿,加之仅有极少数批次(0.072%)劣于FIFO且幅度有限。这些节省与参与者交易额高度正相关,显示优化成果在不同银行间基本按交易规模成比例分布。


4.5 单日表现
接下来展示样本中某个典型日期(2017 年 9 月 20 日,批次大小 n = 70)的聚合最大净借方头寸变化情况,如下所示:

一天开始时,随着参与者发送支付,聚合 mNDP 急剧上升;随着时间推移,mNDP增长趋缓。在当天的许多批次中,没有参与者的 mNDP 发生变化,因此重新排序无法带来流动性节省,这些情况在图中的聚合 mNDP 曲线中表现为平坦的区段。有时单个批次中出现的大额支付(或一组大额支付)可能会使CQM求解器与FIFO的聚合 mNDP 值趋同,从而抹去CQM在当天早些时候实现的节省。上图中 14:20 和更极端的 16:05 就是这种情况。这种“节省消失”现象,除非增加队列大小或采用更复杂的队列构建算法(允许支付在不同队列之间移动以形成更大的图循环并抵消结算大额支付所需的流动性),否则无法避免。显然,对于给定的批次大小,不同批次之间差异很大,在这种简单的预处理设置下可实现的改进是有限的。
下图展示了每个参与者的借方和贷方余额随交易顺序的变化情况。每条线代表一个银行在按既定顺序逐笔完成交易后余额的变化。由于优化的是聚合 mNDP,因此希望限制参与者余额下降到零以下的幅度。在这个例子中,Bank 14 的原始 mNDP 为 1700 万,通过优化重排交易,避免了 Bank 14(蓝线)出现任何借方,同时不增加其他参与者的负担。这样,结合其他银行的交易重排,系统在这 70 笔交易中总共节省了 1800 万的聚合 mNDP。不过需要注意的是,这个批次中的并非所有交易都可优化。如 Bank 13(青色)和 Bank 16(橙色)仅有支出交易,因此无法通过调整顺序来优化它们在该批次中的 mNDP。

最后将批次大小加倍至 n = 140,在两个测试日(2017 年 9 月 20 日和 2017 年 10 月 12 日)运行该算法。与表 1 类似,让FIFO与CQM从相同初始条件开始,整日每个批次分别用FIFO和CQM顺序结算,并在当天结束时报告 mNDP。如下表所示,增大批次大小带来了可观的节省提升。如预期的那样,可优化批次数占潜在可优化批次数的比例在两天中均提高了近 15%,这显然是由于批次中可回收的流动性增多,以及单批次网络图中付款方与收款方之间的连接性增强。

在 2017 年 9 月 20 日,平均、 中位数和最大节省分别提升了约 45%、172% 和 53%;2017 年 10 月 12 日,平均和中位数节省分别提升了约 105% 和 263%,而最大节省几乎没有变化。不过,最大节省这一指标高度依赖于当日最大支付是否被分配到同一队列中,因此预期其稳定性最低。但这两天的日终节省分别增加了约 3.2621 亿加元(+978%)和 1.9184 亿加元(+97%)。这些显著变化可归因于更大批次规模整体性能的提升,以及中途节省损失的减少。特别是在 2017 年 9 月 20 日。
五、总结与展望
本文的核心目标是探索利用混合经典–量子退火技术(D-Wave 混合 CQM 求解器)优化大额支付系统中的支付顺序,以减少系统流动性需求。文中以加拿大 LVTS 系统的30天真实支付数据为样本,设计了一个基于队列重排的优化框架,并将其与传统 FIFO 排序进行比较。
实验结果显示,当前的混合量子计算方案在合理批次规模下(n ≤ 140)可以显著节省流动性,在全样本中平均每日可节省 2.399 亿加元,单日最高节省超过 12 亿。大部分节省分布与银行的交易规模高度相关,且仅有极少数批次结果劣于 FIFO,这些劣化可通过重新运行或回退消除。研究还表明,批次大小是性能的关键限制因素,求解时间随批次规模呈立方增长,当前技术下可在实时约束内求解的最大批次规模约为 140 笔。
论文作者提出了以下多条改进路径供将来的研究工作参考:
1. 批次构建策略优化:当前使用的是简单的“按到达顺序累积”方式,未来可研究更复杂的预处理算法,使批次内的支付网络更均衡、互联性更强,从而提高优化潜力。
2. 动态批次大小:根据交易流和网络结构实时调整批次规模,以在计算时间限制与节省潜力之间取得平衡。
3. 跨队列支付重排:未来系统可允许支付在不同批次间移动,以便形成更大的循环抵消效应,应对大额支付对流动性的冲击。
4. 量子硬件发展:随着量子退火机拥有更多纠缠量子比特,未来混合求解器可以搜索更大的状态空间,从而支持更大批次的优化并获得更高节省。
5. 实时系统集成:探索将该优化方案嵌入实际支付系统的可行性,包括处理延迟、稳定性和操作风险等问题。
这项研究不仅展示了量子计算在金融市场基础设施优化中的实际潜力,也为将量子算法引入其他复杂金融优化问题(清算、结算、风险管理等)提供了借鉴。
原文链接:https://arxiv.org/pdf/2209.15392 | 









