本帖最后由 Jack小新 于 2025-9-12 19:03 编辑
《 Coding schemes in neural networks learning classification tasks 》发表于 Nature Communications 。文章聚焦神经网络分类任务中的特征表示,在贝叶斯框架下研究全连接宽神经网络。研究发现,线性网络会形成模拟编码方案;非线性网络中,Sigmoid 网络呈现冗余编码,ReLU 网络为稀疏编码。且在 MNIST 等实验中,不同编码方案的网络泛化表现存在差异,如 ReLU 网络在小数据集上泛化性较好。这揭示了网络属性对涌现表示的深刻影响。

神经网络具备生成任务相关特征表示的关键能力。事实上,在适当的尺度下,神经网络的监督学习可以产生强有力的、与任务相关的特征学习。然而,这些涌现表示的性质仍不清楚。为了理解学习对表示的影响,我们在贝叶斯框架下研究了学习分类任务的全连接宽神经网络,其中学习塑造了网络权重的后验分布。与先前发现一致,我们对特征学习状态(也称为“非惰性”状态)的分析表明,网络获得了强烈的、数据相关的特征,被称为“编码方案”,其中神经元对每个输入的响应主要由其类别归属决定。令人惊讶的是,编码方案的性质关键取决于神经元的非线性。在线性网络中,出现了任务的模拟(analog)编码方案;在非线性网络中,强烈的自发对称破缺导致了冗余编码方案或稀疏编码方案。我们的研究结果强调了网络属性(如权重的尺度以及神经元非线性)如何深刻地影响涌现表示。
一、研究背景与问题提出
深度学习在实践中的成功与其理论理解之间始终存在落差。虽然我们可以访问神经网络的全部参数与训练任务,但神经元如何协作形成有效的表示仍是悬而未决的问题。
两个核心问题始终困扰研究者:
1. 神经网络到底学到了哪些特征?
2. 这些特征是如何被神经元具体表征的?
传统研究往往通过核函数方法(kernel methods)来描述学习后的表示。这种方法能够捕捉输入之间的相似性,但会“平均掉”神经元层面的细节结构。因此,它无法回答:为什么某些神经元只对特定类别敏感,而另一些神经元却对所有类别有响应?
本研究正是为了解决这一问题,作者在贝叶斯后验框架下分析了宽神经网络的分类学习,提出了一个新的解释工具:
编码方案(Coding Schemes)——定义为“一个神经元对哪些类别敏感”。当我们观察整个神经元群体时,每个神经元的响应集合共同构成了网络的编码方案。
二、核心理论与研究方法
1. 惰性与非惰性网络
· 惰性网络:输出仅依赖随机特征,学习对表示的改变很弱(图1b,1c)。
· 非惰性网络:学习产生强烈的、任务依赖的特征表示(图1d,1e)。
研究重点放在非惰性网络,因为这是表示学习真正发生的地方。
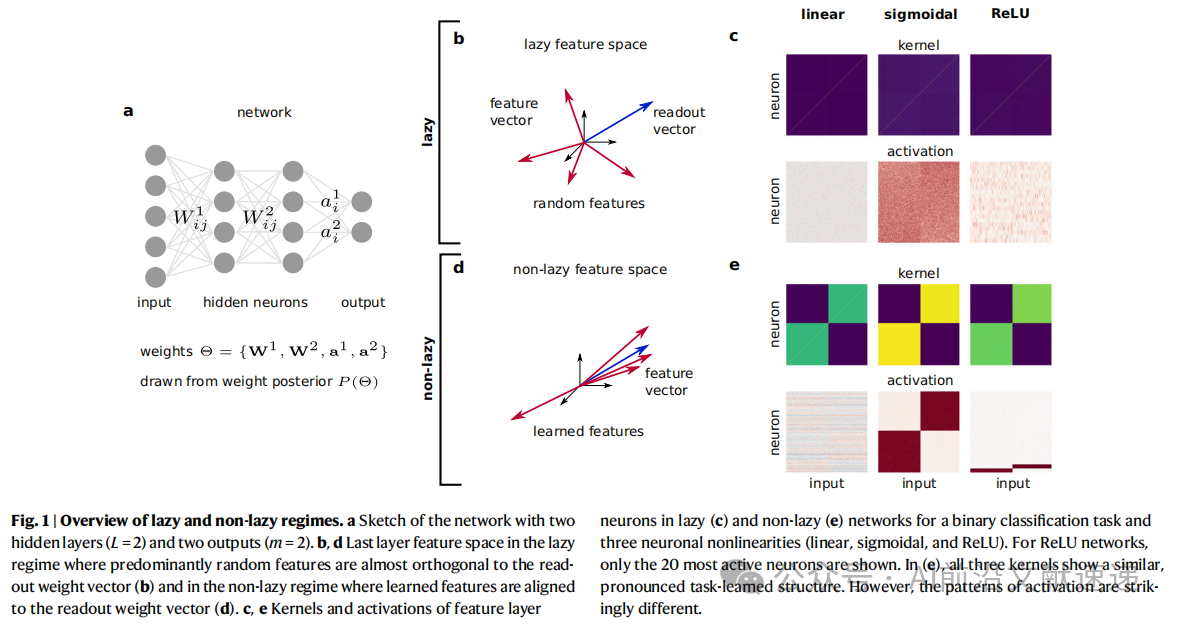
2. 贝叶斯后验框架
· 假设训练结束后,网络参数从一个后验分布中抽样。
· 这一视角允许分析:典型解空间中的表示结构是什么样的。
3. 分析对象
· 全连接宽神经网络,在极限 N,P→∞N, P \to \inftyN,P→∞。
· 激活函数分别取:线性、Sigmoid、ReLU。
· 通过推导单神经元的权重与激活的后验分布,揭示网络形成的编码方案。
三、主要发现与机制解析
1. 三类编码方案(图2,图3)
线性激活 → 模拟编码
· 所有神经元对所有类别都有响应,但响应强度连续变化。
· 表现为一种“渐变式”的编码结构。
Sigmoid 激活 → 冗余编码
· 大量神经元共享相同的类别组合。
· 表示层中的编码模式会随层数加深而“锐化”,类内差异逐渐收敛。
ReLU 激活 → 稀疏编码
· 少数“异常点”神经元承担关键任务,其余神经元大多与任务无关。
· 类似于“特征选择”,网络把主要表达权集中在少数神经元上。
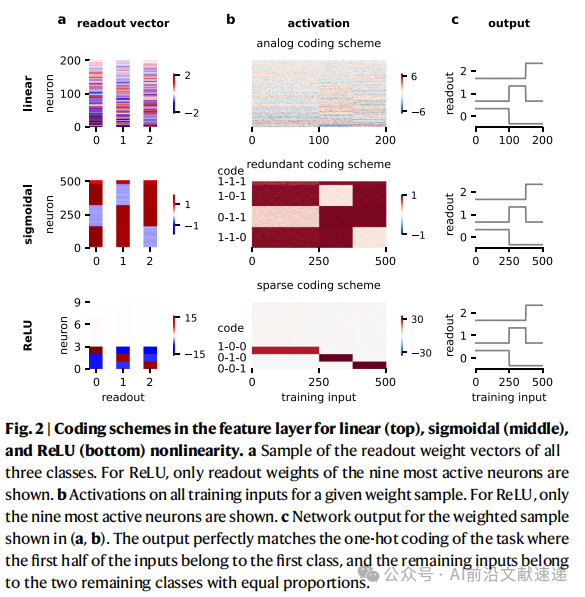
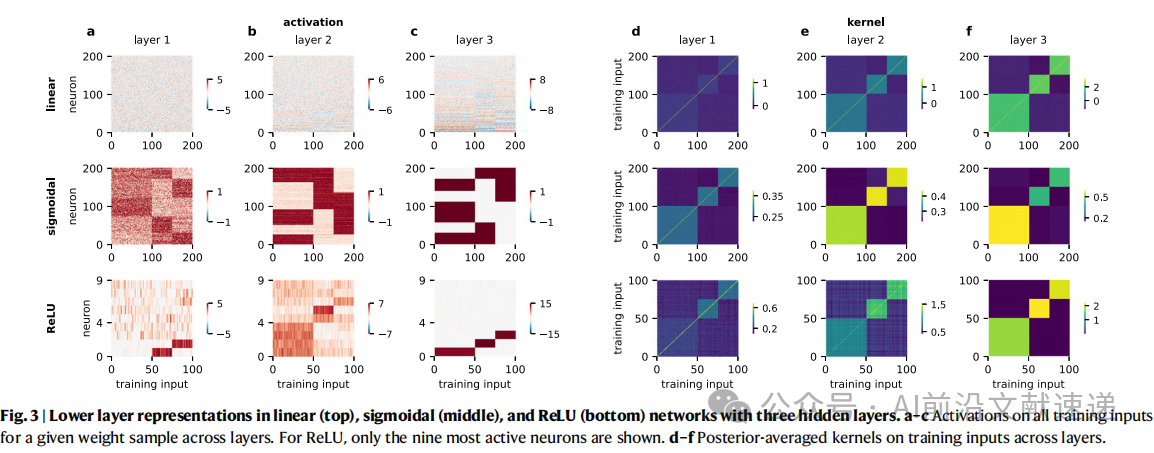
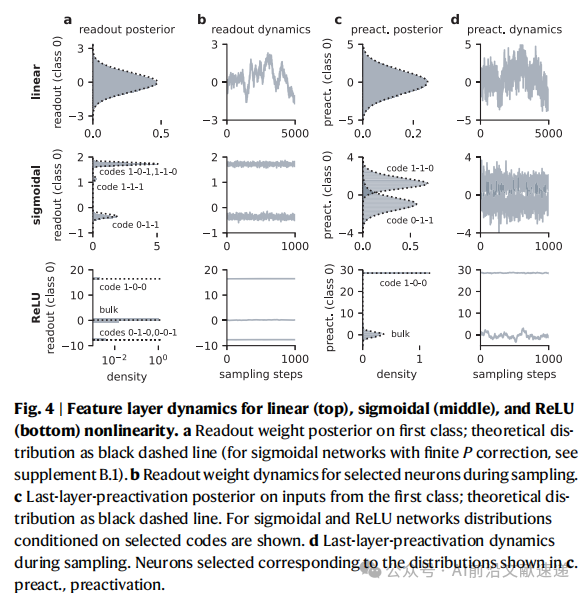
2. 对称性破缺的作用(图4,图5)
Sigmoid 与 ReLU 网络:权重后验分裂成多个分支 → 不同神经元被“锁定”在不同编码模式,导致 遍历性破缺 和 排列对称性破缺。
线性网络:分布保持单峰高斯,对称性不被破坏。
编码方案的出现,本质上是训练过程中发生了对称性破缺,使得神经元群体分化为不同的功能角色。
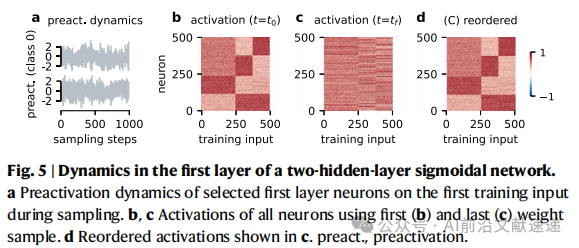
3. 与神经坍缩的联系(图6)
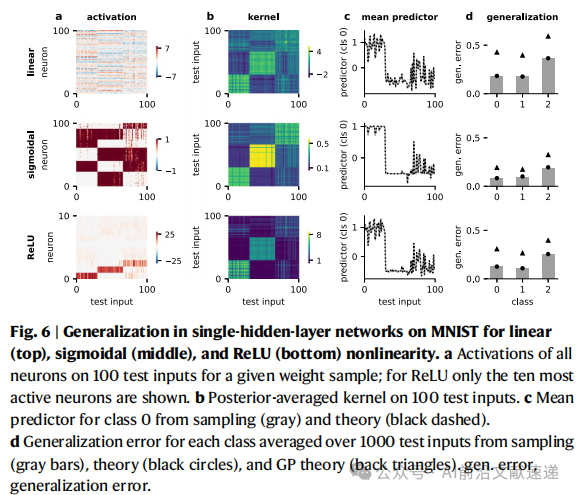
神经坍缩现象:类内收缩、类间等距。
本研究发现:Sigmoid 的冗余编码、ReLU 的稀疏编码,天然能解释这种结构。但它们提供了更细致的神经元级别解释,而不仅仅是最后一层的整体几何结构。
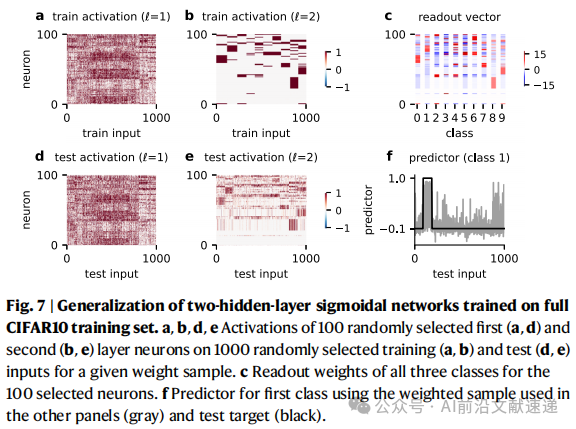
4. 泛化性能的差异(图7)
线性网络:均值预测与高斯过程相同,改进来自方差减小。
Sigmoid 网络:在 MNIST 上形成冗余编码并能泛化;在 CIFAR-10 上则不足,需要更大数据或更深结构。
ReLU 网络:稀疏编码在小数据集上泛化好,但在复杂任务中受限。
四、理论价值与应用启示
1. 理论贡献
· 提出“编码方案”作为新框架,突破了 kernel 方法的局限。
· 揭示了表示学习与对称性破缺之间的机制性联系。
· 解释了神经坍缩背后的结构来源。
2. 实践启示
· 小样本/简单任务 → ReLU 稀疏表示可能更优。
· 大样本/复杂任务 → Sigmoid 冗余表示更稳健。
3. 激活函数选择
· 正则化设计:L2 + ReLU 就能自发形成稀疏表示,无需 L1。
· 迁移学习与小样本学习:清晰的编码方案(冗余或稀疏)更利于表示迁移。
结论
我们发展了一种针对非惰性网络权重后验的理论,在无限宽度和数据集大小极限下,推导出了关于单个神经元权重和激活的解析表达。这些单神经元后验揭示了学习到的表示通过不同的编码方案嵌入到网络中。此外,我们利用这些单神经元后验推导了训练与测试输入上的平均预测器与平均核函数。我们将理论应用于两个分类任务:一个简单的玩具模型(使用正交数据和随机标签)以及图像分类任务(MNIST和CIFAR-10),以研究泛化。在这两种情况下,理论结果与权重后验的经验采样高度一致。
我们证明了:神经元嵌入学习表示的方式表现出显著结构——编码方案,不同神经元群体由激活它们的类别子集来刻画。编码方案的细节强烈依赖于非线性:线性网络呈现模拟编码方案,Sigmoid 网络呈现冗余编码方案,ReLU 网络则呈现稀疏编码方案。在多层网络中,编码方案出现在所有层,并在层间逐步“锐化”;最后一层的编码方案与单层情况相同。我们建立了对称性破缺与神经表示性质之间的直接联系。
关键数据与资源
代码开源:https://doi.org/10.6084/m9.figshare.26539129
DOI:https://doi.org/10.1038/s41467-025-58276-6
文章改编转载自微信公众号:AI前沿文献速递
原文链接:https://mp.weixin.qq.com/s/oDw3c9wrQjvMJUynQo9MPw?scene=1 | 








