本帖最后由 哈奇一 于 2025-10-9 16:42 编辑
伊辛模型作为统计物理学中的经典框架,不仅成功解释了铁磁材料的相变现象,更在量子计算、优化算法和艺术创作等领域展现出惊人的跨界潜力。本文带您穿越百年科学史,从伦茨和伊辛的原始构想出发,探索该模型如何从解释磁性的简单工具,发展为连接量子计算与艺术纹理生成的通用语言。

伊辛模型的恩斯特·伊辛肖像
什么是伊辛模型 Ising Model?
伊辛模型是统计物理中最著名的模型之一,在二维及更高维度中表现出在临界温度下的相变。它模拟了从铁磁体到神经网络的各种现象。
量子伊辛模型的起源可以追溯到20世纪初,当时威廉·伦茨提出了一个简单的晶格模型来理解铁磁性,他的学生恩斯特·伊辛在1925年分析了它的一维形式。
虽然伊辛的初步结果在一个维度上没有显示出长程秩序—似乎令人沮丧,但它为对统计力学的更深入探索奠定了基础。
后来的突破,如克莱默斯-万尼尔对偶性1941和拉尔斯·昂萨格对二维经典伊辛模型的精确解(1944),揭示了丰富的相变行为,并将该模型确立为理论物理学的基石。
量子版本的飞跃是随着横向磁场的引入而实现的,该磁场将自旋转化为非交换量子算子。
这种修改导致了横场伊辛模型 TFIM,使物理学家能够研究量子涨落如何与相互作用能竞争,特别是在出现量子相变的零温度下。
量子伊辛模型通过将硬组合问题转化为物理问题来帮助优化:最小化能量。二元决策变量映射到自旋,目标加上成对约束映射到局部域和耦合。
“最佳”解是伊辛哈密顿量的基态—因此找到最优就变成了找到最低能自旋构型。
该映射涵盖了整个 QUBO 系列(Max-Cut、路由、调度、投资组合选择、特征选择等),这就是为什么 Ising 模型是用于现实世界优化的通用编码。
动画模拟伊辛模型?
通过实验,量子伊辛模型已经在不同的平台上实现,从捕获离子和里德堡原子阵列到超导量子比特。
这些系统允许对相互作用强度和横向场进行受控调整,从而能够直接观察临界点、激发光谱和纠缠增长。
除了实验室结构之外,类似 TFIM 的行为还存在于量子磁体、某些铁电材料和分子自旋系统中,显示出其在合成和自然环境中的相关性。
它的重要性远远超出了基础物理学。在量子计算中,许多困难的优化问题可以表示为找到伊辛哈密顿量的基态。
这种映射是量子退火和绝热量子计算的核心,其中 TFIM 充当“驱动”哈密顿量,慢慢演化为问题哈密顿量。TFIM的光谱特性和动态直接影响此类算法的性能、运行时间和成功概率。
在门模型范式中,量子近似优化算法 QAOA等算法使用基于伊辛的成本函数以及受 TFIM 启发的混合器。
了解 TFIM 动力学有助于设计高效的时间表、选择参数以最大限度地提高解决方案质量以及探索可能增强算法性能的非随机驱动因素。
这使得量子伊辛模型不仅仅是一个理论结构,而且是一个量子算法工程师的实用设计工具。
该模型在量子计算中的应用非常广泛:金融中的投资组合优化、运筹学中的交通流和物流、机器学习中的特征选择,甚至计算生物学中的蛋白质折叠。
基于硬件的伊辛机和混合经典量子求解器都依赖于 TFIM 框架来建模、映射和解决这些问题。这种普遍性使该模型成为跨行业问题编码的通用语言。
量子伊辛模型之所以受欢迎,是因为它击中了一个罕见的最佳点:它足够简单,可以进行深入分析,但又足够丰富,可以捕捉基本的物理和现实世界的计算。
在凝聚态物质中,它是量子相变、对偶性和纠缠的首选游乐场;在实验室中,它很容易在捕获离子、里德堡原子阵列和超导量子比特上实现,这些量子比特带有用于调整相互作用和场的干净旋钮。
在计算方面,它通过量子退火、绝热算法和 QAOA 提供了从硬优化QUBO/Ising 成本函数到硬件的直接桥梁,使其成为对设备进行基准测试和设计启发式方法的通用语言。
如今,量子伊辛模型已成为一个统一的概念:足够简单,可以解决关键情况,足够丰富,可以捕捉复杂现象,并直接适用于新兴的量子算法领域。
对于任何从事量子技术工作的人来说,了解 TFIM 既是了解量子物质的窗口,也是计算创新的蓝图。
1920年,德国物理学家威廉·伦茨Wilhelm Lenz试图寻找一个简化的模型来解释为什么磁体在受热到一定程度时会“去磁”。
他设想了一个磁偶极子阵列,这些偶极子具有“自旋”,可以指向向上或向下(用箭头表示):
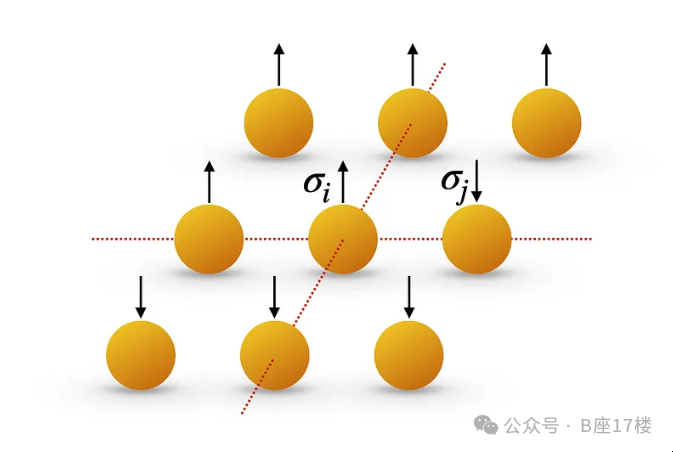
伊辛模型中用于模拟铁磁材料的二维磁偶极子阵列,自旋向上或向下。
从概念上讲,如果大多数自旋方向一致,那么对齐的偶极子场会融合形成磁体。随着自旋随机化(通过加热),场会倾向于相互抵消,从而使大尺度磁性消失。
伦茨指派他的研究生恩斯特·伊辛Ernst Ising来推导数学模型,这成为伊辛的论文Ising 1925。
伊辛进一步简化了模型,将其简化为一个一维偶极子链,其中两个最近邻会对一个偶极子的自旋产生影响。
他的分析表明,即使在低温下,所有的自旋也不会完全对齐。伊辛和伦茨都认为二维或三维阵列的结果会相同,因此该模型被认为是失败的描述性理论而被搁置。
物理学家拉尔斯·昂萨格Lars Onsager在1940年代重新研究了该模型,关注二维阵列中四个最近邻对偶极子自旋的影响。
他在1944年发表了解决方案,证明二维模型能够解释磁性随温度的变化,甚至展示了一个临界温度,标志着向去磁状态的相变Onsager 1944。
这个被称为伊辛模型的理论最初被提出作为磁体的卡通式描述。如今,它作为物理系统的简单模型被广泛使用,物理学家将其比作生物学中的模式生物——果蝇。
一本最近出版的教科书称伊辛模型为“几乎可以用来模拟所有有趣热力学现象的系统”。
它还渗透到远超物理学的众多领域,成为地震、蛋白质、大脑甚至种族隔离的模型。(Wood 2020)
在讨论物理系统建模方法时,问一句“你试过伊辛模型了吗?”几乎成了默认做法。
对于更高维度模型(三维及以上)难以找到闭合解的问题,促使人们使用模拟方法,如强大的Metropolis-Hastings算法。
Metropolis-Hastings算法
Metropolis算法的强大之处在于认识到,有时候你需要先走错方向,才能最终到达目的地。
在伊辛模型中,随机或算法选择一个自旋点并计算其能量。然后翻转该自旋并计算新能量。
如果新能量更低,则接受翻转的自旋(使整个自旋系统的能量状态降低)。
然而,不是直接拒绝较高能量状态,而是根据能量差异和一个比例因子,以一定概率接受较高能量状态。
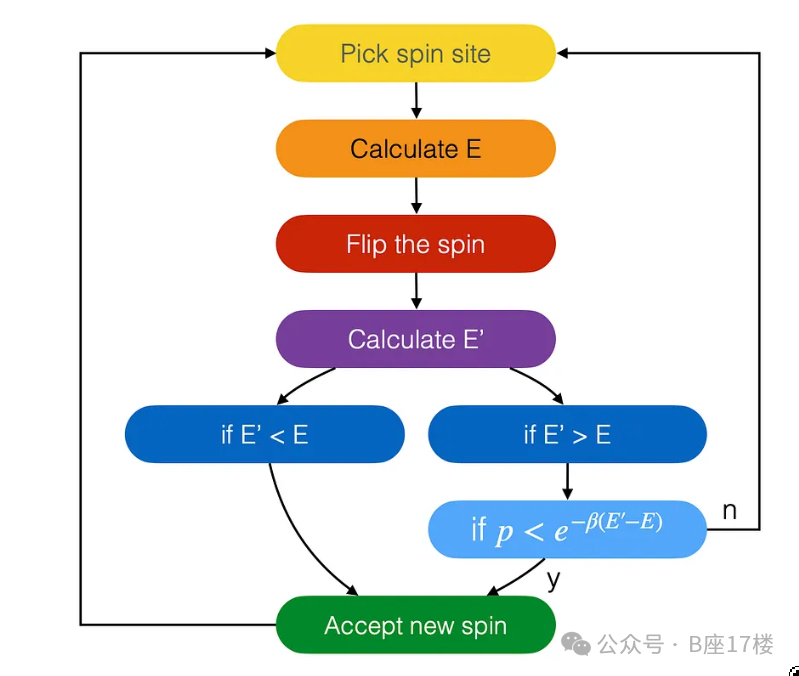
Metropolis-Hastings算法流程图 | 来源:J. van Saders
这个简单算法通过偶尔“走错路”避免陷入局部能量最小值!
上述比例因子通常与温度的倒数相关。这导致在高温下接受较高能量状态的概率更大,从而模拟了热诱导自旋翻转的效果(参见维基百科作为了解底层数学的起点)。
相变区域
以一个200×200自旋点的环面为例,可以将其展开为具有周期边界条件的二维平面(即顶部边缘实际上与底部边缘相邻),下面的图像展示了温度的影响。
在每种情况下,初始自旋是随机的,进行了100次迭代,每次迭代以随机顺序更新所有点,使用Metropolis-Hastings算法。

伊辛模型的单调(T<Tc)、有趣(T=Tc)和混乱状态(T>Tc)。(来源:J. van Saders)
拉尔斯·昂萨格(Onsager 1944)证明了上述二维模型在临界温度Tc(约为2.269)以上从有序到无序发生相变。
从美学角度看,最有趣的图案出现在临界温度Tc处。低于此温度是单调的均匀性,高于此温度则是混乱。一般来说,最有趣的事情发生在均匀与混乱的边界处。
用伊辛模型创造纹理
Yannick Meurice(Meurice 2022)最近发表了一篇有趣的论文(本文的灵感来源!),展示了如何使用伊辛模型生成类似水彩版画的纹理。他通过在伊辛模型中应用外部磁场和选择温度展示了这一点。
温度的影响已在上面展示,但外部磁场尚未讨论。伊辛模型允许对自旋偶极子集合施加外部磁场。应用的简化通常省略外部磁场。Meurice巧妙地使用非均匀外部磁场在自旋状态阵列上施加图像,在他的案例中是阿尔伯特·爱因斯坦的肖像。
虽然Meurice讨论了使用非均匀温度分布的想法,但他将其留作学生的练习。本文接受了这个任务。
通过磁化施加图像
对于研究的200×200阵列,一个+1自旋(以白色表示)的正方形创建了外部磁化模式。经过100次迭代,最初随机的自旋演变为最终状态,展示出通过将温度设为Tc而形成的纹理。

在T=Tc时施加非均匀外部场(来源:J. van Saders)
热梯度施加纹理变化

在伊辛模型上施加热梯度(来源:J. van Saders)
在阵列上施加了从5(右上角)到1(左下角)的热梯度,其中临界温度约为2.269。尽管存在周期边界条件(即顶部和底部边缘实际上是相邻的),但温度梯度影响每个点接受较高能量状态的概率。因此,效果创建了跟随热梯度的纹理。
由此产生的伊辛状态图让我想起了海岸线波浪的高对比度图像。艺术中最著名的波浪是日本浮世绘艺术家葛饰北斋的木版画《神奈川大浪》(1831)。
其分形性质似乎与伊辛模型域结构的缩放有相似之处。构建了一个粗糙的《大浪》掩模图像,并用作热图:

《大浪》的伊辛模型。来源:J. van Saders
虽然这种方法显然需要改进,但你可以看到波浪尖端形成的 интересная текстура 模式具有一定潜力。
在展示了使用伊辛模型的磁化和热梯度后,是时候进入正题了……
恩斯特·伊辛的伊辛模型肖像

来自AIP Emilio Segrè视觉档案的原始肖像,用于提取面部区域。(来源:J. van Saders)
由于阵列限于200×200个点,仅使用了上述伊辛肖像的面部区域。
提取的区域被阈值化以创建二值图像,并对其应用了一些侵蚀和膨胀操作以获得更好的图像。然后将二值图像缩放到[-1, +1]自旋。
使用了上述相同的热梯度,得到了伊辛模型的一对非均匀输入:
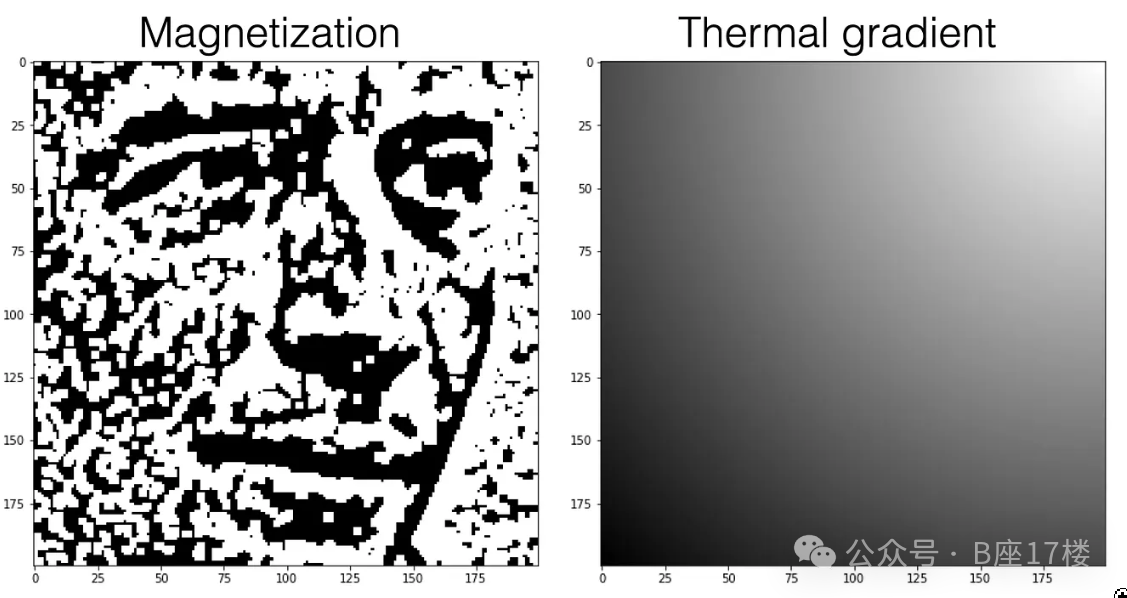
伊辛模型的外部磁化和热梯度输入丨来源:J. van Saders
从随机初始状态开始,Metropolis-Hastings算法迭代100次。最终状态在伊辛模型中呈现了恩斯特·伊辛的有趣渲染。

伊辛-伊辛元肖像丨来源:J. van Saders
结论
本文受Yannick Meurice的启发,展示了伊辛模型如何为图形艺术创造有趣的纹理。遵循他的思路,创建了恩斯特·伊辛的“元”肖像,以庆祝这一具有普适属性的模型诞生100周年。
伊辛模型还在其他艺术项目中找到了应用。George Legrady的《伊辛模型:闪烁与多联画》使用阵列中睁开和闭合的眼睛,创建了伊辛阵列演变的电影:
理解和可视化重整化的一个很好的方法是伊辛模型。
数学家证明相变对称性的普遍存在
一组数学家证明,在临界时刻,一种称为旋转不变性的对称性是众多物理系统的普遍属性。这项关于多孔介质渗透模型的研究与近期相变对称性的重要工作相关。量子杂志专栏文章作者:Allison Whitten 特约撰稿人 2021年7月8日
几何·数学物理·数学·相变·对称性·普适性·所有主题
五十多年来,数学家们一直在寻找一种严格的方法来证明:当物理系统在从一种状态转变为另一种状态的神秘临界点时,一种异常强大的对称性具有普遍性。
这种被称为共形不变性的强大对称性实际上包含三种独立的对称性。
2020年12月,五位数学家团队发表的证明首次近乎证实了共形不变性是这些物理系统在相变过程中的固有特征。
该研究确立了旋转不变性——共形不变性包含的三种对称性之一——在广泛物理系统相变临界点的存在。
"这是重大贡献。这个开放性问题存在已久,"以色列魏茨曼科学研究所的Gady Kozma表示。
旋转不变性是圆形具有的对称性:无论旋转多少度,它看起来都一样。在相变临界点的物理系统中,这意味着系统的许多特性在模型旋转后保持不变。
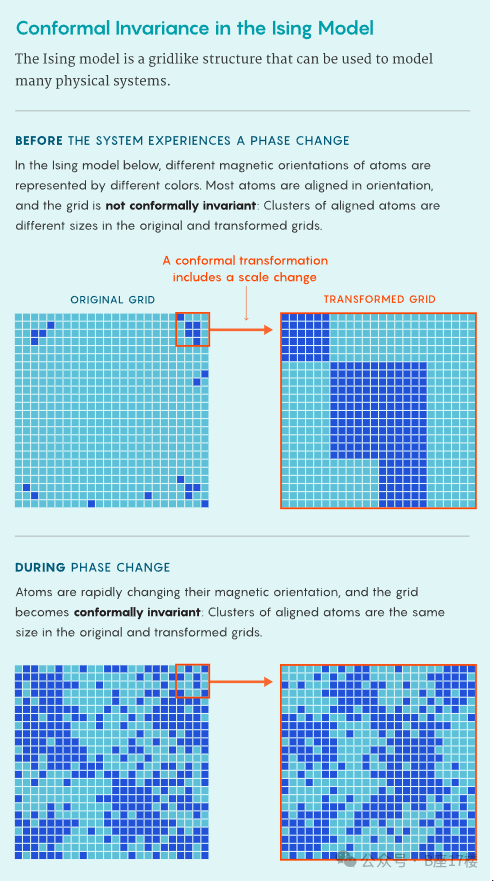
先前的研究成果已证明旋转不变性在两种特定模型中成立,但其方法缺乏普适性。这项新研究首次证明旋转不变性在广泛模型类别中具有普遍性。
"这种普适性结果更引人入胜",因为它表明不同物理系统模型会呈现相同模式,法国高等科学研究所(IHES)和日内瓦大学的Hugo Duminil-Copin表示。他是该研究的五位合著者之一。
这项研究也为证明更宏大的结果带来希望:这些物理模型具有共形不变性。过去几十年数学家已证明共形不变性在几个特定模型中成立,但始终无法证明其普遍性。这项新研究为此类全面结论奠定了基础。
"这已是重大突破",日内瓦大学的Stanislav Smirnov表示,"现在共形不变性似乎触手可及。"
神奇时刻 相变是自然界最迷人的现象之一。有些相变剧烈,如水加热汽化或冷却结冰;而本研究关注的相变则存在模糊的临界区域。
在这个临界点,系统既非前态亦非后态。
以铁磁体加热为例:超过居里温度约540℃时,铁会失去磁性。这个转变源于数百万原子磁矩的随机翻转。伊辛模型将这个复杂过程简化为二维方格上的箭头阵列。
1970年,物理学家Alexander Polyakov预测:尽管微观表现不同,这些系统在临界点都呈现共形不变性。此后数十年间,物理学家确信其正确性,但数学严格证明始终是难题。
对称性之冠 共形不变性包含平移对称性、旋转对称性和尺度对称性。"我称之为'统御一切的对称性',因为它比三者更强大,"Duminil-Copin解释道。
在临界温度下,伊辛模型中原子关联距离突增,各种尺寸的磁畴同时涌现。共形不变性意味着此时对网格进行平移、旋转或缩放都不会改变箭头关联性。
突破性进展 2001年,Smirnov首次严格证明渗流模型在三角格点上的共形不变性。2006年他又证明伊辛模型的共形不变性,这两项突破性工作助他获得菲尔兹奖。但这些证明都依赖特定模型的"魔法"特性。
新研究采用概率论的耦合技术,结合可积系统理论,首次证明旋转不变性在方形和矩形格点渗流模型中的普遍存在。"需要多学科方法多角度攻关,"Duminil-Copin强调。
最后征程 在证明旋转不变性后,研究团队将目标转向尺度不变性。若再证明这一点,结合已有的旋转不变性和无需单独证明的平移不变性,将最终确立共形不变性的普遍性。
"第三步证明很快就会实现,"Duminil-Copin预测,"可能是我们,也可能是更聪明的人,但肯定为时不远。
"虽然旋转不变性的证明耗时五年,但Smirnov对二维共形不变性的证明前景表示乐观:"可能一周,也可能五年,但我比去年十一月乐观多了。"
关键术语对照:
- conformal invariance → 共形不变性
- rotational invariance → 旋转不变性
- phase transitions → 相变
- critical point → 临界点
- Ising model → 伊辛模型
- percolation → 渗流
- universality → 普适性
- lattice → 格点
注:专业术语保持学科规范译法。
最后,但也许是最重要的事情,了解并知道模型的局限,因为人类比自旋系统复杂的多 ... 😄

参考文献
[1] 伊辛E.《铁磁理论的贡献》汉堡论文摘录1925参见http://www.fh-augsburg.de/~harsch/germanica/Chronologie/20Jh/Ising/isi-intr.html
[2] Meurice, Y.《用伊辛模型制作数字水彩版画》美国物理学杂志 90, 87 (2022)
[3] 昂萨格L《晶体统计学 I. 具有有序-无序转变的二维模型》物理评论系列II653-4117-149 (1944)
[4] 维基百科《伊辛模型》https://en.wikipedia.org/wiki/Ising_model
[5] Wood,C.《改变科学的磁体卡通图像》Quanta杂志2020年6月24日
https://www.quantamagazine.org/the-cartoon-picture-of-magnets-that-has-transformed-science-20200624/
[6] Eigenvalue Studio <e|s>Tangibit Studios的品牌,John van Saders是Tangibit Studios的创始人。他热衷于模块化艺术和弗兰克·劳埃德·赖特的建筑。他的安娜堡咨询公司Auxilus Systems利用35年以上的技术经验,将系统思维应用于商业和产品开发。https://medium.com/@TangibitStudios/membership
文章转载自微信公众号:集智俱乐部
原文链接:https://mp.weixin.qq.com/s/75GQxwWFtZT1TyttDkxLZA?scene=1&click_id=1 | 











