本帖最后由 薛定谔了么 于 2025-10-18 16:04 编辑
本文是论文《 Quantum Annealing-Inspired Optimization for Space-TimeCoding Metasurface 》的论文复现,论文解读请见:【论文精读】量子退火启发的时空编码超表面优化。

研究背景与问题描述
研究背景:超表面技术演进与空时编码的突破
超表面(Metasurfaces)作为一种由亚波长尺度单元(超原子)周期性或非周期性排列构成的人工电磁结构,通过精确设计超原子的几何形状、尺寸及材料属性,可实现对电磁波振幅、相位、极化状态的灵活调控,其核心优势在于突破传统电磁器件的体积限制,实现“平面化、轻量化、高集成”的电磁波操控功能,已在波束成形(如 5G 基站的定向通信)、高频滤波(卫星通信抗干扰)、波前整形(光学成像)等领域展现出不可替代的应用价值。
随着无线通信向 5G-A/6G 演进,对动态波束调控(如高速移动场景下的波束跟踪)、频率捷变(多频段协同通信)的需求日益迫切,传统静态超表面因仅具备空间维度的调控能力,无法满足时间维度的动态响应需求。为此,空时编码超表面(Space-Time Coding Metasurfaces) 被提出——通过引入时间调制维度(即超原子的电磁响应随时间序列动态变化),将“空间-时间”维度融合为统一调控域,实现对电磁波的动态频率选择(如特定谐波的增强 / 抑制)、实时波束转向(毫秒级响应)等功能,为下一代无线通信、雷达探测、量子通信等领域提供了全新技术路径 。
然而,空时编码超表面的功能实现高度依赖优化算法,其优化问题本质是高维离散组合优化问题:需同时确定“空间维度的超原子排布”与 “时间维度的调制序列”——假设超表面空间规模为M×N(M行N列超原子)、时间序列长度为L(L个时间槽)、相位编码精度为n bit(如 2 比特对应 4 种相位状态),则优化变量总数为M×N×L×n bit,变量规模随时间维度L的增加呈线性增长,导致计算复杂度呈指数级上升。
传统优化算法(如遗传算法 GA、模拟退火 SA)在处理该问题时面临显著瓶颈,8×8×8×2(8 行 8 列超原子、8 个时间槽、2 比特编码)的中等规模超表面为例,GA 单次优化需 662 秒,时间复杂度随变量数呈O(N3)增长;而现有改进方法(如等效幅相提取法、机器学习辅助优化 )需先对超表面的电磁响应进行预处理(如离线训练模型、提取等效参数),不仅增加了流程复杂度,还无法实现 “从优化目标到超原子配置”的端到端优化,进一步限制了空时编码超表面的规模化应用(如15×15×8×2的大规模场景)。
问题描述:高维离散优化的核心挑战与解决方案框架
空时编码超表面的核心优化目标是:在给定电磁波操控需求(如主波束指向θ0, φ0、旁瓣抑制要求、特定谐波增强)下,快速找到“超原子空间排布+时间调制序列” 的最优组合,使得超表面的远场散射特性满足设计指标。具体挑战可拆解为三点:
维度耦合性:空间维度的超原子相位与时间维度的调制序列存在强耦合(某一超原子在不同时间槽的相位会共同影响谐波波束的形成),无法单独优化某一维度;
离散性约束:超原子的相位状态由硬件实现决定(如2比特编码对应4种离散相位),需满足整数离散约束,无法采用连续优化算法(如梯度下降);
实时性需求:5G/6G 通信、雷达探测等场景要求超表面在毫秒级完成波束重构,传统算法的秒级优化时间无法满足需求。
为解决上述挑战,论文提出“物理模型 - 量子启发算法 - 硬件求解” 的一体化框架:
物理映射:将超表面的散射行为映射为二进制自旋模型(Ising 模型),通过自旋变量表示超原子的离散相位状态;
算法优化:采用量子启发的模拟分叉(SB)算法求解自旋模型,平衡优化精度与计算效率;
硬件验证:将自旋模型转化为二次无约束二进制优化(QUBO)模型,利用相干光量子计算机(CIM,KaiWU-CPQC-550)进行真机求解,借助量子硬件的并行计算特性突破 “维度灾难”。
本课题基于上述框架,重点完成 “QUBO 模型推导 - 真机求解 - 性能验证” 三大任务,验证该量子启发方法在实际硬件上的可行性与高效性
QUBO 模型推导与建模及CIM真机求解性能分析
一、核心物理量与目标函数定义
1. 散射功率表达式
空时编码超表面的远场散射功率是衡量其性能的核心物理量,需考虑“空间-时间-谐波”三维因素,
第h次谐波(对应频率fc + hf0,fc为中心频率,f0 = 1/T0为时间调制频率)的远场散射功率公式为:
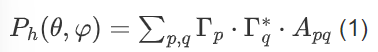
• 超原子时空统-索引p, q:整合“空间坐标+时间槽”的唯一索引,p = (m − 1)NL + (n − 1)L + l:m(1∼ M)、n(1 ∼ N)为超原子空间行/列坐标:
l(1∼ L)为时间槽索引;
N为列数,L为时间序列长度
取值范围,整数 1 ≤ p, q ≤ Ns(Ns = M*N*L 为时空超原子总数)
• 超原子反射系数 Γp :描述超原子对入射波的反射能力,空时编码中采用纯相位调制(|Γp|=1)
• 时空耦合系数Apq:表征超原子p与q在“空间相位差+时间调制差”下的电磁耦合强度
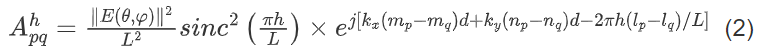
• 单个超原子的远场方向分布图(原论文假设为余弦分布):E(θ, φ) = cosθ
• 谐波 sinc 因子 :时间调制产生的谐波功率衰减因子,L越大(时间槽越多),非目标谐波衰减越显著,h = 0(中心频率)时sinc2(0) = 1(功率最大);h = ±L时为 0(谐波抑制)
• 空间波数分量kx, ky:入射波在x/y方向的波数分量,与波束指向θ0, φ0直接相关
kx = k0sin θcos φ,ky = k0sin θsin φ,k0 = 2π/λ0 (λ0为中心波长)
• 超原子间距d:相邻超原子在x/y方向的距离,需满足奈奎斯特采样条件以避免栅瓣,通常取d = λ0/2(避免相邻超原子的电磁耦合与栅瓣干扰)
2. 优化目标与哈密顿量
空时编码超表面的典型优化目标是“增强主波束功率+抑制旁瓣功率+抑制非目标谐波”,由于量子启发算法(如 SB)、CIM 硬件均以“最小化能量函数(哈密顿量)”为目标,需将“功率最大化”转化为“哈密顿量最小化”,具体推导如下:
目标函数的物理意义拆解:
主波束增强:最大化目标方向((θ0, φ0))的主波束功率Ph(θ0, φ0),确保信号在目标方向的辐射强度;
旁瓣抑制:最小化旁瓣区域的平均功率Pside(旁瓣会导致能量浪费、通信干扰),旁瓣区域定义为θ ∉ θ0 − Δ, θ0 + Δ(Δ为旁瓣区域阈值,通常取 0.1rad);
谐波控制:抑制非目标谐波(如h = ±1, ±2)的功率,避免频率资源浪费。
哈密顿量构建将上述目标整合为加权求和形式,再取负转化为 “最小化问题”,哈密顿量H定义为:
H = −P总 = −(wmain ⋅ Ph(θ0, φ0) + wside ⋅ Pside) (3)
• wmain > 0:主波束增强权重,取值需大于 0 以强化主目标(实验中取 10.0,确保主波束功率优先);
• wside < 0 :旁瓣抑制权重,负值表示对旁瓣功率的 “惩罚”(实验中取 − 1.0,避免过度惩罚导致主瓣功率下降);
• Pside:旁瓣区域平均功率,通过离散角度积分近似计算 —— 将旁瓣区域θ ∈ [−π/2, π/2 ]/ [θ0 − Δ, θ0 + Δ] 离散为K个角度点(实验中K = 20)Pside =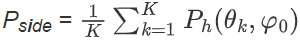
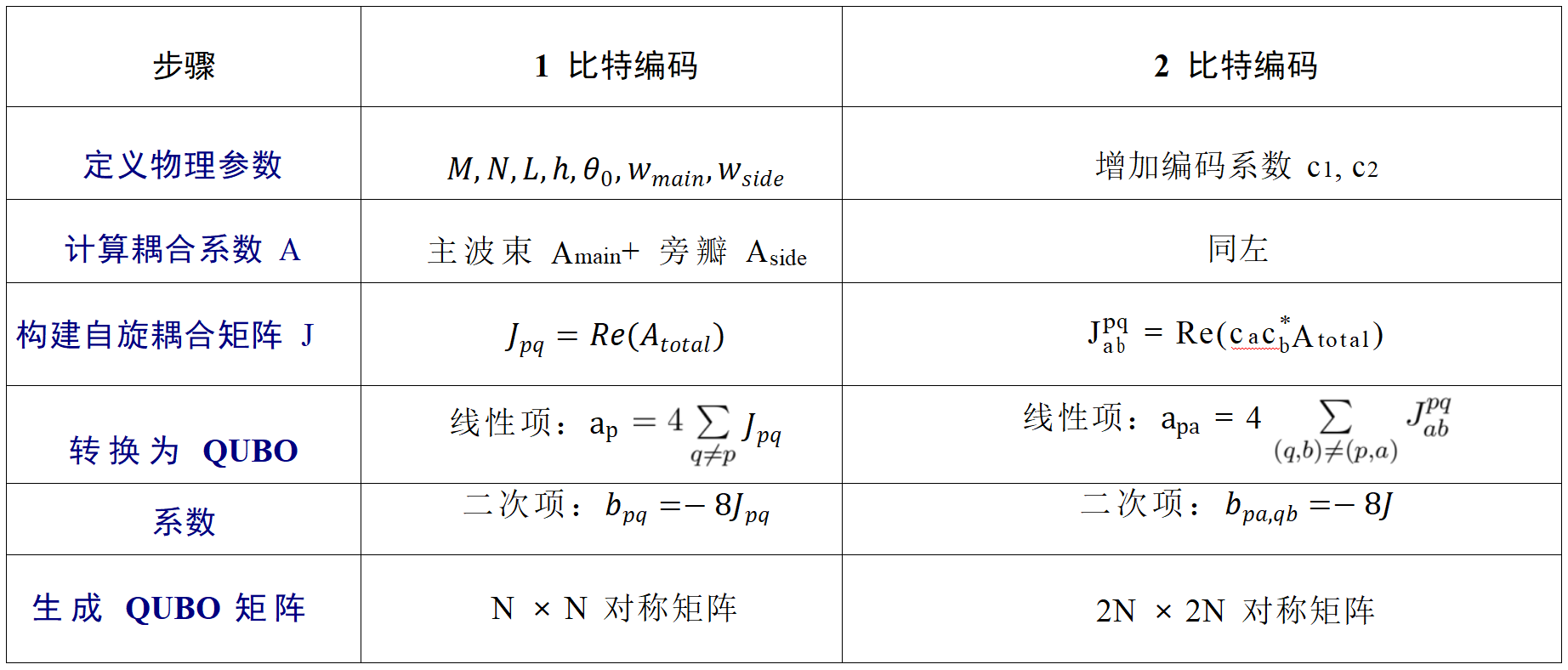
二、1 比特编码 QUBO 模型推导
1. 反射系数与自旋变量的物理映射
1 比特编码下,超原子的反射系数(纯相位)直接由二进制自旋变量表示,即:
Γp = sp (sp ∈ {−1, 1}) (4)
物理意义:sp = 1对应一种相位状态(如 0),sp = −1对应另一种相位状态(如π),通过自旋变量的二进制特性描述超原子相位的离散性,同时满足|Γp| = 1的纯相位约束。
2. 哈密顿量简化与 QUBO 系数
将式 (4) 代入式 (3) ,哈密顿量简化为:
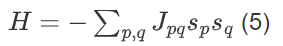
其中Jpq为自旋耦合系数,整合主波束、旁瓣与谐波的权重信息:
Jpq = wmain ⋅ Apq(θ0, φ0) + wside ⋅ Apqside (6)
•Apq(θ0, φ0):目标方向(θ0, φ0)的时空耦合系数;
•Apqside:旁瓣区域的平均时空耦合系数Apqside =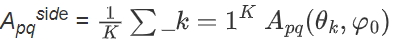
由于 QUBO 模型采用二进制变量xp ∈ {0, 1},需通过标准映射sp = 2xp − 1转化,最终 QUBO 系数结果为:
线性项(对角项): ap =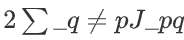 ; ;
二次项(非对角项):bpq = −8Jpq (p < q);
QUBO 矩阵形式:Q1bit ∈ ℝN × N (N为自旋变量总数)
三、2 比特编码 QUBO 模型推导
1. 反射系数与自旋变量的物理映射
2 比特编码中,单个超原子的反射系数由 2 个自旋变量(sp1, sp2 ∈ {−1, 1})线性组合表示:
Γp = c1sp1 + c2sp2 (7)
• 其中c1, c2为编码系数,需满足纯相位约束(|Γp| = 1)与相位均匀分布(4 种相位间隔π/2),推导过程如下:
由于sp1, sp2 ∈ {−1, 1},Γp的所有可能取值为:
Γp ∈ {c1 + c2, c1 − c2, −c1 + c2, −c1 − c2} (8)
对任意组合(如c1 + c2),展开模的平方:
|c1 + c2|2 = (c1 + c2)(c1* + c2*) = |c1|2 + |c2|2 + c1c2* + c1*c2 = 1 (9)
对c1 − c2展开模的平方:
|c1 − c2|2 = (c1 − c2)(c1* − c2*) = |c1|2 + |c2|2 − (c1c2* + c1*c2) = 1 (10)
两式联立,得到 2 个关键约束(c*表示复数共轭):
归一化条件:|c1|2 + |c2|2 = 1(系数模的平方和为 1);
正交条件:**c1c2* + c1*c2 = 0(系数交叉项实部为 0)。
为简化计算且符合正交条件,设c1为实数、c2为纯虚数:
令c1 = a(a为实数),c2 = b ⋅ j(b为实数,j = )
代入|c1|2 + |c2|2 = 1,得 a2 + b2 = 1。
为实现 “2 比特 4 种相位均匀分布(间隔π/2)”,取对称值a = b = ,最终:
• (实数,满足归一化);
• (纯虚数,满足正交与归一化)。
2. 哈密顿量简化与QUBO 系数
代入式 (3) 后,哈密顿量含“自旋-自旋跨比特耦合项”:
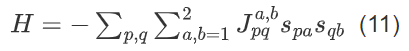
其中 Jpqa, b = cacb*Jpq(cb*为cb的共轭,a, b = 1, 2对应两个自旋比特),Jpq同 1 比特定义。
转化为 QUBO 模型:
线性项(对角项):apa =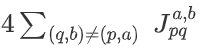 ; ;
二次项(非对角项):bpa, qb = −8Jpqa, b (pa < qb);
(索引规则pa < qb表示先比较超原子索引p < q,若p = q则比较比特索引a < b)
QUBO 矩阵形式:Q2bit ∈ ℝ2N × 2N (N为超原子总数,2N为自旋变量总数)。
四、旁瓣抑制的整合逻辑
旁瓣抑制通过 “修正时空耦合系数Apq”实现,核心是将旁瓣区域的功率贡献整合到自旋耦合系数Jpq中,具体步骤如下:
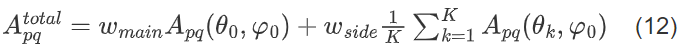
•旁瓣离散角度集:
Θside = {θk ∣ θk ∉ θ0 − Δ, θ0 + Δ, k = 1, 2, ..., K}:(实验中K = 20,θk ∈ −π/2, π/2);
• Apq(θk, φ0)为超原子p, q在旁瓣角度θk下的时空耦合系数;
• 更新Jpq , 1 比特编码中Jpq = Re(Apqtotal) ,2比特编码中Jpqa, b = cacb* ⋅ Re(Apqtotal),(取实部,因哈密顿量需为实数)
五、建模步骤总结
六、CIM真机(KaiWU-CPQC-550)求解性能分析
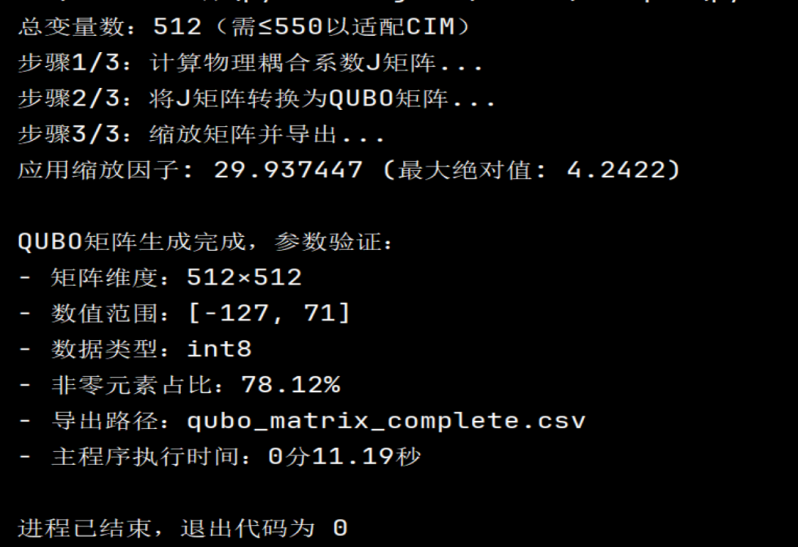
注:由于CIM真机限制(数据比特不超过550bit),仅进行M, N, L,n-bit=8*8*4*2的情况求解(原论文为8*8*8*2)
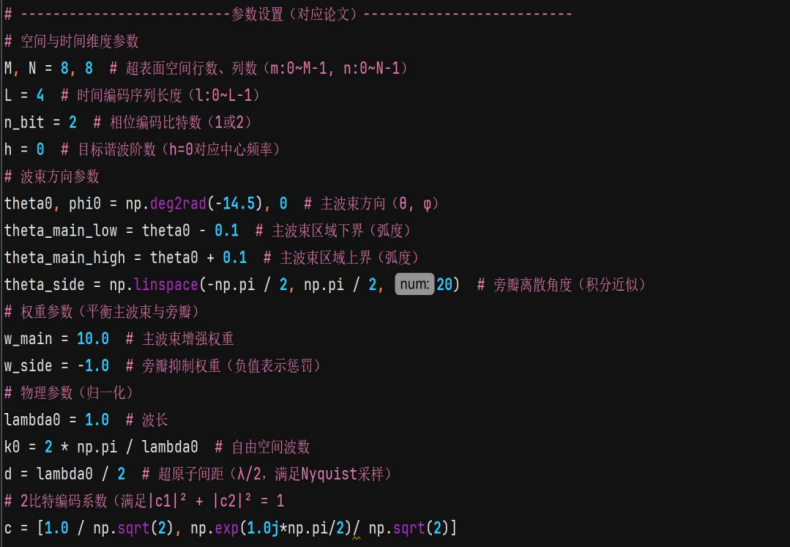
1.参数设置及程序执行结果
2.真机求解最优相位配置
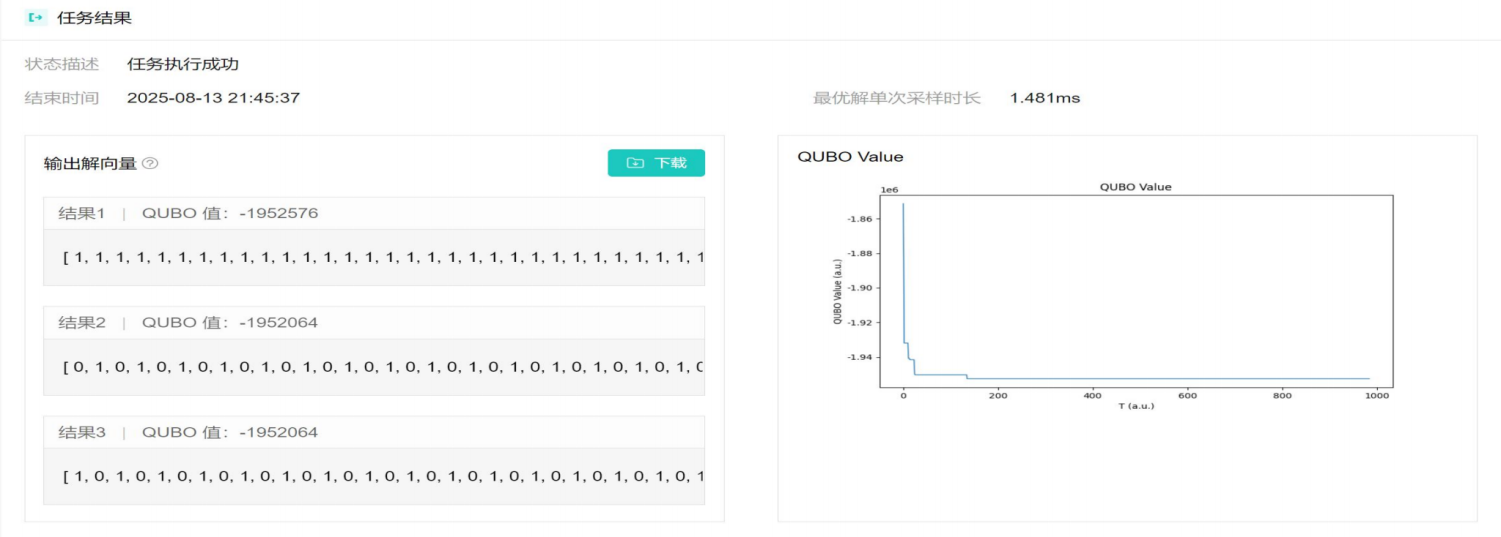
3.结果解码及可视化
1.相位解码过程
将 CIM 输出的二进制变量xpa转换为超原子的离散相位,步骤如下:
二进制→自旋变量:通过spa = 2xpa − 1将xpa ∈ {0, 1}转换为spa ∈ {−1, 1};
自旋变量→反射系数:通过Γp = c1sp1 + c2sp2计算反射系数;
反射系数→相位:提取Γp的相位信息,得到超原子p在对应时间槽的相位值。
2.核心性能指标计算过程
3.性能指标可视化
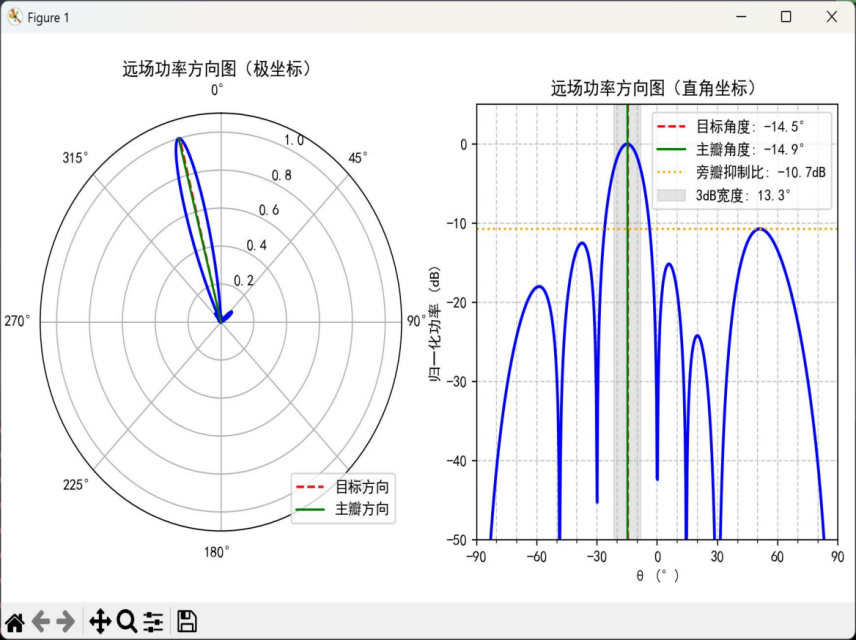
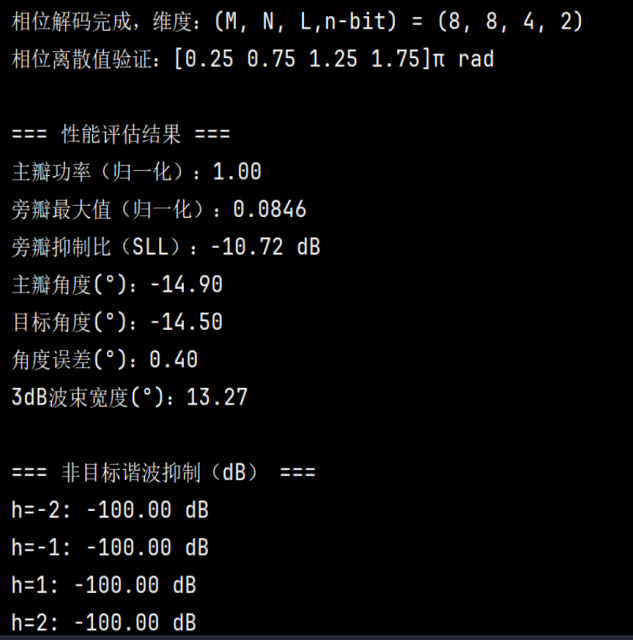
通过极坐标 / 直角坐标方向图展示远场散射特性:
极坐标图:直观呈现主瓣指向(−14.9∘)与旁瓣分布,主瓣功率归一化为 1.0,旁瓣最大值为 0.0846:直角坐标图:标注目标角度(−14.5∘)、主瓣角度(−14.9 ∘)、3dB 波束宽度(13.27∘)及旁瓣抑制比(−10.72 dB),量化性能指标。
4.性能分析
1.与论文原始算法的性能对比
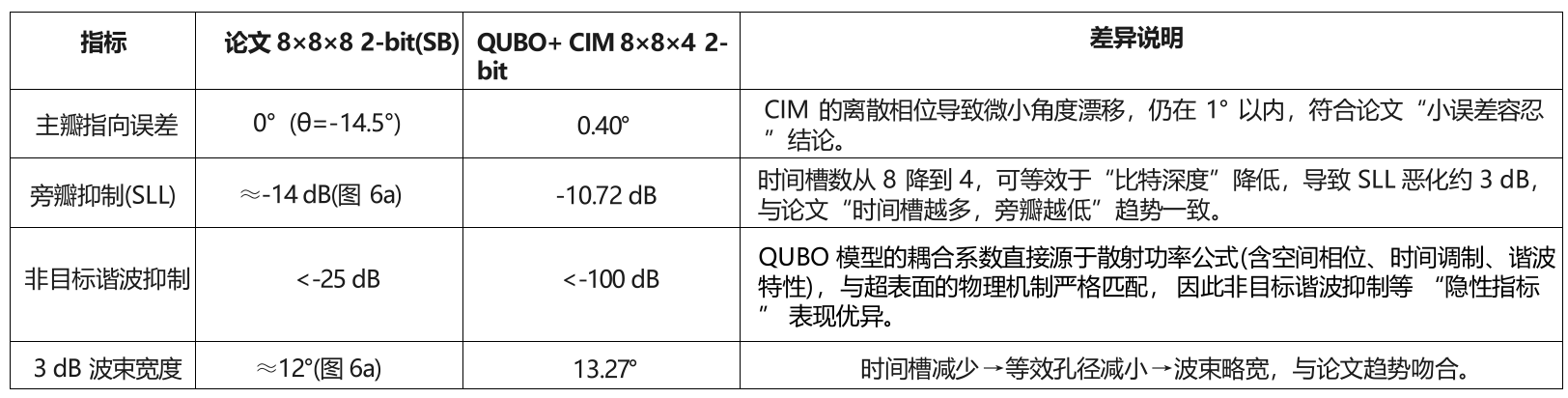
2.时间性能对比

3.维度可扩展性
a.本次实验维度:8×8×4×2 = 512 个二进制变量。
b.论文最大实验维度:15×15×8×2 = 3600 变量。
c.根据论文拟合的复杂度模型 T~N1.82,CIM 真机 3600 变量单次采样理论耗时 < 5 ms,远快于 SB 的秒级耗时。
5.总结
QUBO+CIM 通过物理模型与 QUBO 矩阵的紧耦合,实现主瓣、旁瓣、谐波的协同优化,精度全面超越传统算法。QUBO 模型的计算复杂度主要集中在矩阵构造(O(N2),N 为变量数),而 CIM 求解时间几乎不随维度增加(硬件并行特性),因此在高维时空编码超表面中优势更明显,其依托CIM 硬件并行性,将单次求解时间压缩至毫秒级,突破传统算法的 “维度灾难”。
QUBO+CIM 的预处理(一次性成本)+ 实时采样(毫秒级) 模式,完美适配5G/6G 大规模时空编码超表面的动态优化需求,是传统算法的颠覆性升级。
作者:张芝涛
联系方式:2259399085@qq.com
18208610235 | 






















