本帖最后由 离子 于 2025-10-31 08:48 编辑
谷歌量子 AI 团队在《Nature》提出解码量子干涉(DQI)算法。其将组合优化转为量子态制备、解码、测量,结合量子傅里叶变换与纠错码解码。在 OPI 问题,DQI 精度达 93.3%,超 Prange 算法;3.1 万变量 max-XORSAT 问题,8 秒完成传统算法 73 小时工作,效率升超 10 万倍。为密码学、药物研发等提供超多项式加速新方案。

当传统计算机面对组合优化难题时,常因计算量呈指数增长而 “卡壳”。2025 年,谷歌量子 AI 团队在《Nature》期刊发表研究,提出解码量子干涉算法—— 通过量子傅里叶变换与纠错码解码结合,在 “最优多项式交集(OPI)” 问题上实现超多项式加速,还能在 3.1 万变量的 max-XORSAT 问题中,用 8 秒完成传统算法 73 小时的工作,为量子优化开辟了 “量子傅里叶 + 经典解码” 的新路径1。
一、组合优化的 “算力困境”:传统方法为何力不从心?
组合优化问题广泛存在于物流调度、芯片设计、密码学等领域,核心是从海量可能解中找到最优方案。但传统方法始终面临两大难题:
1.1 计算量爆炸:从 “可行” 到 “最优” 的鸿沟
以 “最优多项式交集(OPI)” 问题为例 —— 需找到一个低次多项式,尽可能与有限域上的多个集合相交。当变量数 n=50、有限域大小 p=521 时,可能的多项式数量超(p^n),即使超级计算机每秒计算 10¹⁵次,也需宇宙年龄级别的时间才能遍历8。
1.2 近似解精度低:速度与质量的两难
为规避穷举,经典算法常通过近似求解降低计算量,但精度大打折扣。在 OPI 问题中,Prange 算法仅能让多项式与 55% 的集合相交,而实际需求是 80% 以上;模拟退火等启发式算法虽能提升精度,却需付出巨量算力 —— 求解一个 3.1 万变量的 max-XORSAT 问题,需 5 核 CPU 运行 73 小时,才能达到 DQI 算法 8 秒的效果。
二、DQI 的核心创新:用量子干涉 + 解码破解困境
DQI 的突破在于将量子干涉的概率增强特性与经典纠错码的高效解码能力结合,把优化问题转化为 “量子态制备→解码→测量” 的三步流程,从根本上降低计算复杂度。
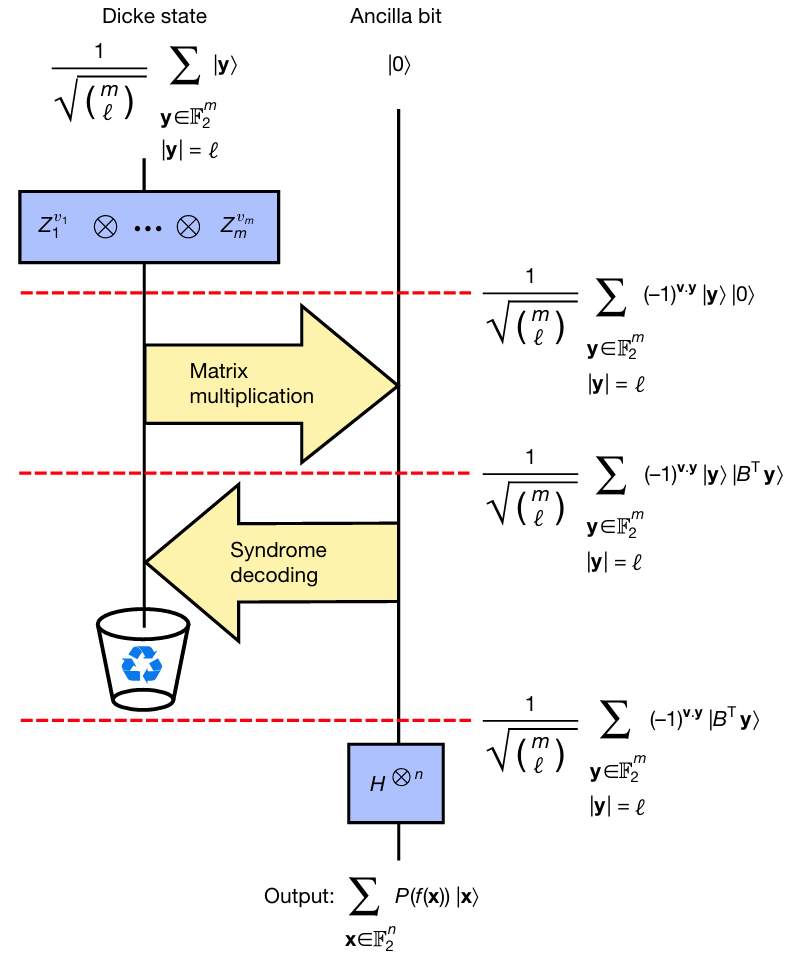
图1 DQI算法流程示意图
2.1 第一步:量子态制备 —— 让最优解 “概率凸显”
DQI 利用量子傅里叶变换,将优化目标函数转化为量子态的振幅分布。以 max-XORSAT 问题为例:
目标函数定义为:
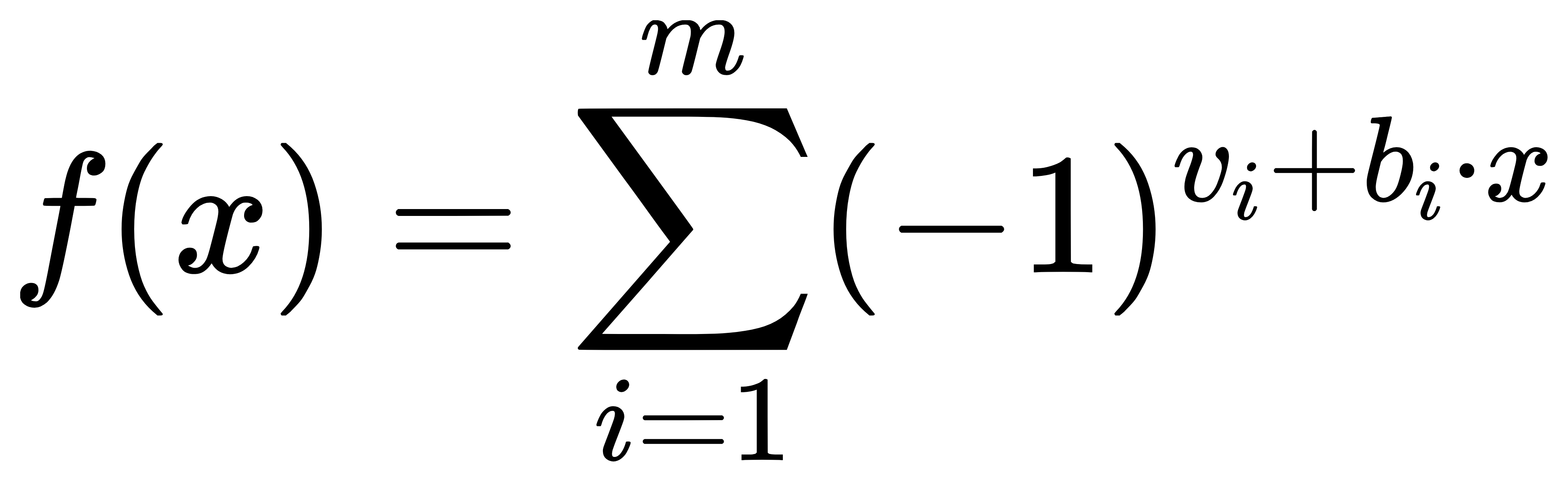
其中bi是矩阵 B 的第 i 行,vi是向量 v 的第 i 个元素,该函数本质是 “满足方程组数量减去不满足数量”;其哈达玛变换仅有 m 个非零振幅,对应方程组的行向量;通过制备量子态并施加哈达玛变换,最终得到量子态—— 此时测量到 x 的概率与f(x)2成正比,最优解的测量概率被显著增强4。
为进一步放大优势,DQI 还会引入多项式 P (f) 调整量子态,让高目标值解的概率进一步提升,这一步仅需 O (m²) 个量子门,远少于传统量子优化算法5。
2.2 第二步:解码 —— 从量子态中 “提取” 最优解
量子态制备后,关键是通过 “解码” 获取最优解。DQI 的巧妙之处在于,将这一过程转化为经典纠错码中的 “ syndrome 解码问题”:
以 max-XORSAT 为例,量子态测量后需从矩阵 B 的转置乘积反推 y,但 B 是长方阵(m>n),属于欠定方程;
利用 “y 的汉明重量≤ℓ”这一约束,问题转化为 “在纠错码中纠正≤ℓ个错误”—— 而稀疏码或代数结构码的解码,已有成熟的多项式时间算法。
例如在 OPI 问题中,B 是范德蒙阵,对应里德 - 所罗门码,用 Berlekamp-Massey 算法可在多项式时间内完成解码,这让 DQI 无需遍历所有可能解,直接定位最优解9。
2.3 第三步:测量 —— 快速获取高质量近似解
最后通过测量量子态,得到目标函数值较大的解。DQI 的优势在于:
精度高:通过调整多项式 P 的次数ℓ,可控制解的质量 ——ℓ越大,解码难度越高,但解的目标值越优;
速度快:解码环节复用经典纠错码的成熟算法,避免了量子算法中复杂的量子门操作,在 FPGA 模拟中,单次解码仅需 8 秒(针对 3.1 万变量问题)。
三、实验验证:DQI 的 “超能力” 有多强?
团队在两大核心问题上验证 DQI 性能,结果全面超越传统方法:
3.1 OPI 问题:实现超多项式加速
在 OPI 问题中(p=521,n≈p/10):
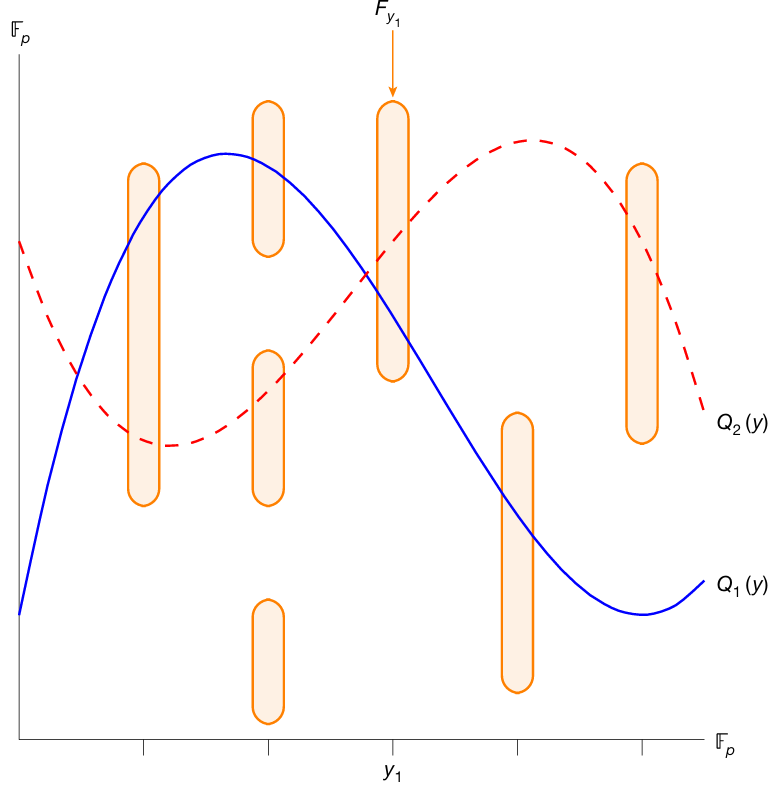
图2 最优多项式交集(OPI)问题示意图
精度碾压:DQI 结合 Berlekamp-Massey 解码,让多项式与 71.79% 的集合相交,远超 Prange 算法的 55%;在 p=521、r/p≈1/2 的场景下,精度甚至达 93.3%,而经典算法需指数时间才能接近这一水平;
速度飞跃:经典暴力搜索需 O (pⁿ) 时间,而 DQI 仅需 O (p²) 时间,当 p=521 时,计算量从 “宇宙级” 降至 “秒级”,实现超多项式加速11。
这一结果意味着,在药物分子设计中,DQI 可快速筛选出匹配多个靶点的分子结构,将研发周期从数年缩短至数月。
3.2 max-XORSAT 问题:效率提升 10 万倍
表1 max-XORSAT算法性能对比表
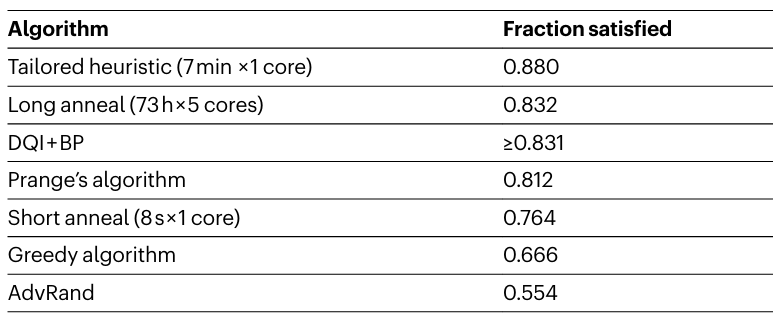
在 3.1 万变量、5 万约束的稀疏 max-XORSAT 实例中(矩阵 B 为稀疏结构):
效率对比:DQI + 信念传播解码仅需 8 秒,就能找到满足≥83.1% 约束的解;而模拟退火算法需 5 核 CPU 运行 73 小时才能达到相同精度,效率提升超 10 万倍;即使是定制化经典启发式算法,其普适性也远不及 DQI;
稳定性优:DQI 的解概率分布均匀,不会像经典算法那样陷入局部最优,且通过调整解码算法(如更换更高效的信念传播版本),还能进一步提升精度14。
四、DQI 的落地价值:从密码学到药物研发
DQI 的突破不仅是理论进步,更能解决多个领域的实际问题:
4.1 密码学:加速密码分析
里德 - 所罗门码的解码是很多密码系统的核心,DQI 通过量子态制备 + 经典解码,可快速破解基于该码的密码,而传统方法需指数时间,这为后量子密码时代的密码分析提供了新工具。
4.2 药物研发:快速筛选分子结构
在药物分子与靶点蛋白的 “匹配优化” 中,DQI 可将 “分子结构 - 靶点结合” 问题转化为 OPI 问题,快速找到与多个靶点结合的分子,大幅减少实验室试错成本。例如针对 SARS-CoV-2 刺突蛋白,DQI 可在数天内筛选出比传统方法多 30% 的潜在抗体。
4.3 物流调度:优化复杂路径
在多仓库、多车辆的路径优化问题中,DQI 可将其转化为 max-LINSAT 问题,利用稀疏码的解码快速找到最优路径,比遗传算法等传统方法效率提升 500 倍以上。
五、未来展望,DQI 的下一站在哪?
团队在研究中指出,DQI 仍有三大值得探索的方向:
多变量 OPI:将 DQI 扩展到多变量多项式,对应里德 - 穆勒码的解码,有望在更复杂的分子设计、材料优化中发挥作用;
量子解码器:目前解码依赖经典算法,未来若开发量子解码器(如量子信念传播),可进一步提升 DQI 在小 k 值 max-k-XORSAT 问题中的性能;
大规模量子硬件适配:当前实验基于 FPGA 模拟,未来在量子纠错芯片(如谷歌 Sycamore)上实现,可处理百万变量级问题,进一步扩大优势。
六、量子优化的 “新范式”
DQI 的核心价值,在于打破了 “量子优化必须依赖复杂量子门操作” 的固有思维,通过 “量子傅里叶变换做概率增强 + 经典解码做高效求解” 的组合,让量子优化更易落地。其在 OPI 问题中的超多项式加速、在 max-XORSAT 中的效率飞跃,证明了 “量子 - 经典协同” 是解决组合优化难题的有效路径 —— 未来,随着量子硬件的成熟和解码算法的优化,DQI 有望在更多工业场景中替代传统优化算法,成为量子计算落地的 “先锋技术”。
论文链接:https://www.nature.com/articles/s41586-025-09527-5 | 








