本帖最后由 Jack小新 于 2025-1-23 16:02 编辑
算力网络,简单来说,就是将计算能力像水电一样进行输送的网络。想象一下,我们平时使用的手机、电脑等设备,都需要处理器来计算和运行各种程序。而算力网络就像是一个超级大的“处理器仓库”,它将分散在各地的计算资源整合起来,通过互联网进行优化分配,以满足不同用户和场景的计算需求。
举个例子,当我们观看高清视频、玩大型游戏或者进行复杂的数据分析时,这些操作都需要大量的计算能力。算力网络就像是一个智能的“电力系统”,能在短时间内为我们提供所需的计算资源,确保我们的使用体验流畅、高效。这样一来,我们就可以随时随地享受到强大的计算能力,而不用担心设备性能不足的问题。
算力网络面临的挑战
•资源分配效率: 算力网络需要高效地分配计算资源以满足不同用户和应用的多样化需求。这要求网络能够实时监测资源使用情况,并动态调整资源分配策略,以避免资源闲置或过载。
•网络延迟: 计算任务的快速响应需要低延迟的网络环境。算力网络必须解决数据在网络中传输的延迟问题,特别是在处理实时性要求高的应用时,如自动驾驶等。
•成本要低: 搭建和维护算力网络需要投入大量资金,所以需要在保证性能的同时,尽量降低成本。
算力网络的组成部分
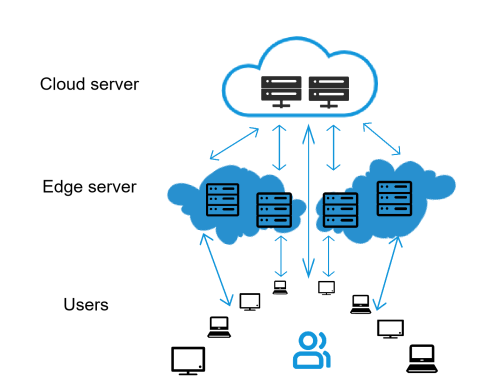
算力网络主要由三个部分组成:
•端侧设备: 也就是各种智能设备,它们负责收集数据。
•边缘服务器: 位于设备附近,负责处理部分数据,并减轻云端服务器的负担。
•云端服务器: 位于数据中心,拥有强大的计算能力,负责处理更复杂的数据。
赛题内容
考虑一个特定区域的算力网络布局优化问题。将区域划分成若干相邻正方形网格,算力需求分布数据提供了各个网格内的算力需求。数据中的坐标值为所在网格的中心坐标,为简化问题,将各网格内的算力需求点统一到所在网格中心点(即可认为是一个网格对应一个需求点)。
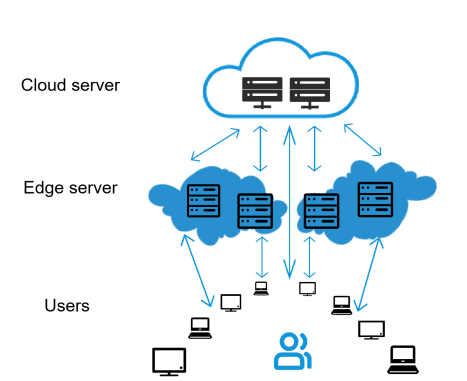
网格内的算力需求由端侧设备产生,端侧设备是连接到网络的终端设备,例如传感器、智能手机、工业机器人等。算力网络中的算力需求由边缘服务器和云端服务器满足。边缘服务器位于网络的“边缘”,通常靠近终端用户或设备。它们的任务是在离用户更近的地方处理数据,以提高响应速度和效率。边缘服务器可以更快地处理请求,因为它们距离用户更近。边缘服务器可以减轻核心云基础设施的负担,提高整体操作效率。云端服务器位于远离用户的数据中心,具有强大的计算和存储能力。当边缘服务器容量不足时,云端服务器可以作为补充。边缘服务器和云端服务器之间的协同作用可以优化整个系统的性能和可靠性。
问题1: 在问题1中我们只考虑由边缘服务器满足计算区域内的需求。 假设要在算力需求分布的网格区域内开设2个边缘服务器,每个边缘服务器的覆盖半径为1。 要求建立QUBO模型,确定在哪些点放置边缘服务器可以覆盖最多的算力需求。
问题2: 当边缘服务器无法满足算力需求时,将由上游云端服务器提供计算服务。现在网格区域外部增设云端服务器,端侧和边缘服务器可以选择连接到云端节点,当边缘服务器接受的计算需求超过容量限制时,边缘服务器多余的需求将直接被分配到云端服务器。 每个端侧节点的算力需求都必须被满足,且只能由一个服务器服务,这个计算节点可以是云端节点,也可以是边缘服务器。由于边缘服务器存在资源容量上限约束,假设每个边缘服务器的可用计算资源容量为12,云端服务器的可用计算资源容量为无穷大, 即不考虑云端服务器的可用计算资源限制。服务器存在一定的覆盖半径,假设边缘服务器的覆盖半径为3,云端服务器的覆盖半径为无穷大,即不考虑云端服务器的覆盖范围。
开设边缘服务器通常需要成本,该成本由固定成本,计算成本和传输成本组成。其中固定成本与是否开设以及开设位置有关;计算成本与请求的计算资源量成正比,计算方法为:单位计算成本乘以计算量。云端服务器的单位计算量成本为1,边缘服务器的单位计算量成本为2。 同时,从端侧到边侧、从边侧到云侧、从端侧到云侧之间的传输也存在传输成本,传输成本计算方式为:传输的算力需求量乘以传输距离乘以单位传输成本,其中传输距离的计算使用欧式距离保留两位小数,按照单边距离计算(不考虑往返传输)。从端侧到边侧以及从边侧到云侧的单位传输成本为1,从端侧到云侧的单位传输成本为2。
如果要满足区域内全部的端侧算力需求,建立QUBO模型,求解给出整体成本最小的算力网络布局,即边缘服务器的位置、数量,以及端侧到边侧、边侧到云侧和端侧到云侧节点之间的连接关系。
问题本质
在算力网络布局优化问题中,表面上看,我们可能会联想到经典的资源调度问题或网络流优化问题,并尝试通过传统的贪心算法或动态规划方法来求解“如何在不同区域间分配资源以最小化成本”。这些方法或许能够帮助我们找到某一时刻的局部最优解,但这个问题的复杂性远超表面。我们不仅需要考虑每个计算节点的资源分配,还要全局性地优化整个网络的布局,保证每个资源都得到合理利用,并且在多个区域之间保持高效的计算和通信。
深入分析
算力网络布局优化问题的核心是如何在整个网络中找到一种资源分配和节点布局的最优方案,类似于在图G上寻找最优的计算节点布局和通信路径组合。这实际上是一个组合优化问题,需要从所有可能的网络布局中挑选出最优解,而这些可能的布局数目是巨大的。例如,如果我们有n个潜在的边缘服务器部署位置和m个计算任务点,那么这些位置和任务的组合数量将以指数级别增长,即n^m种可能的布局方式。
显然,简单的穷举法是不现实的,因为即使是中等规模的网络,其组合数量也是天文数字,远远超出了经典计算机的处理能力。就像旅行商问题中的路径选择一样,我们在这里面临着一个排列组合的难题,网络中的每个节点和资源配置都可能影响整体的优化结果。
换句话说,随着问题规模的扩大,算法的时间复杂度呈现非多项式增长,难以在合理时间内求解。由此可见,问题的关键并不在于如何局部优化某一个资源配置,而在于如何全局性地优化整个算力网络的布局,找到那条能够最小化整体计算成本的最优布局路径。这个问题的复杂性不仅仅是计算量的增加,更在于需要在多维度上同时进行优化,寻找全局最优解。
第一问参考模型
第一问重述
在一个4x4的网格中,每个网格代表一定的计算需求区域。我们的目标是确定在哪些网格中部署边缘计算节点,以便最大化覆盖的用户需求。
符号定义

决策变量

目标函数
最大化总覆盖的计算需求量:

约束条件
•每个用户网格的覆盖状态不超过其周围边缘节点的覆盖状态:

•部署的边缘计算节点总数等于 :

简化模型(容斥原理)

第二问参考模型
问题概述
•6×6的网格,每个网格内都有一定的计算需求(只有11个网格中的计算需求为非零值),需要满足所有计算需求
•5个开设边缘服务器的候选位置,边缘服务器具有计算容量限制; 当边缘服务器接收的计算请求超过容量时,将多出的计算请求发送给云端服务器
•1个位置开设了云端服务器,云端服务器无容量限制
•用户可以连接边缘服务器或者云端服务器(只能连一个); 边缘服务器容量不够可以连接云端服务器
•最小化成本:固定成本 + 可变成本(计算成本) + 传输成本(=单位成本*距离*传输量)

符号定义

中间变量

决策变量

数学模型
目标函数:

其中


约束条件:
•算力需求点被分配到边侧或云侧,且只被一个服务

•覆盖关系,且只有开了边侧才可以从需求点连接

•边侧连接云侧和开启边侧的关系

•当且仅当边侧服务器 收到的计算需求超过其容量限制时, 取值为

预处理

参考代码
第一问代码
class CIMSolver:
# 准备数据
def prepare_data(self,path):
# 初始化一个字典来存储算力需求分布数据
DEM = {}
path = os.path.join(path, '算力需求分布数据_test.csv')
# 打开一个CSV文件,读取算力需求分布数据(替换成自己的路径)
with open(path, 'r') as f:
reader = csv.reader(f, delimiter=',', quotechar='|')
# 跳过文件头
next(f)
# 遍历每一行数据
for row in reader:
# 将算力需求数据存储在DEM字典中,键为位置坐标,值为算力需求
DEM[(row[0] + ',' + row[1])] = int(row[2])
# 创建一个列表,包含所有的位置坐标
LOC_SET = list(DEM.keys())
# 初始化一个字典来存储位置之间的距离
DIST = {}
# 遍历所有位置坐标,计算每对位置之间的距离
for i in LOC_SET:
for j in LOC_SET:
# 计算欧几里得距离
DIST[(i, j)] = np.sqrt((int(i.split(',')[0]) - int(j.split(',')[0])) ** 2 + (int(i.split(',')[1]) - int(j.split(',')[1])) ** 2)
# 设置边缘计算节点的覆盖半径
RANGE = 2
# 设置目标边缘计算节点个数
P = 2
# 初始化一个字典来存储位置之间的覆盖关系
ALPHA = {}
for i in LOC_SET:
for j in LOC_SET:
# 如果距离小于等于覆盖半径,则ALPHA为1,否则为0
if DIST[(i, j)] <= RANGE:
ALPHA[(i, j)] = 1
else:
ALPHA[(i, j)] = 0
# 将计算结果存储在类的实例变量中
self.ALPHA = ALPHA
self.DIST = DIST
self.DEM = DEM
self.RANGE = RANGE
self.P = P
# 计算位置坐标的数量
self.d = int(math.sqrt(len(self.DEM)))
# 准备QUBO模型
def prepare_model(self, lam):
# 创建二进制变量数组x和z,用于表示边缘计算节点的位置和需求覆盖情况
self.x = kw.qubo.ndarray((self.d, self.d), 'x', kw.qubo.binary)
self.z = kw.qubo.ndarray((self.d, self.d), 'z', kw.qubo.binary)
# 初始化松弛变量
self.num_bin = 1
self.slack = kw.qubo.ndarray((self.d, self.d, self.num_bin), 'slack', kw.qubo.binary)
# 设置惩罚系数
self.lam = lam
# 定义目标函数,即最小化算力需求的总和
self.obj = sum(self.DEM[f'{i+1},{j+1}']*self.z[i,j] for i in range(self.d) for j in range(self.d))
# 定义第一个约束条件,即边缘计算节点的数量等于P
self.constr1 = (np.sum(self.x)-self.P)**2
# 初始化第二个约束条件的值
self.constr2 = 0
# 遍历所有位置坐标,构建第二个约束条件
for i in range(self.d):
for j in range(self.d):
# 对于每个位置,需求覆盖情况z应小于等于该位置与所有边缘计算节点覆盖关系的总和
self.constr2 += (self.z[i,j]+ np.sum(self.slack[i, j, _]*(2**i) for _ in range(self.num_bin)) \
- np.sum(self.ALPHA[f'{i+1},{j+1}', f'{i1+1},{j1+1}'] * self.x[i1, j1] \
for i1 in range(self.d) for j1 in range(self.d)))**2
# 构建无约束QUBO模型,包括目标函数和惩罚项
Q = self.lam * (self.constr1 + self.constr2) - self.obj
self.model = Q
# 解析QUBO表达式
Q = kw.qubo.make(Q)
# 转化成Ising模型
ci = kw.qubo.cim_ising_model(Q)
self.obj_ising = ci
ising = ci.get_ising()
self.matrix = ising["ising"] # 存储Ising模型的矩阵
# print(self.matrix.size)
bias = ising["bias"] # 存储Ising模型的偏置
def sa(self, ss=None, T_init=1000, alpha=0.99, T_min=0.0001, iterations_per_T=10):
"""
使用模拟退火算法寻找QUBO问题的最优解。
参数:
ss -- 初始解(可选)
T_init -- 初始温度
alpha -- 降温率
T_min -- 最小温度
iterations_per_T -- 每个温度下的迭代次数
返回:
best -- 最优解
"""
# 执行模拟退火算法
output = kw.classical.simulated_annealing(
self.matrix,
s = ss,
T_init = T_init,
alpha=alpha,
T_min = T_min,
iterations_per_T = iterations_per_T)
# 使用最优采样器从模拟退火的结果中获取最优解
opt = kw.sampler.optimal_sampler(self.matrix, output, bias=0, negtail_ff=True)
best = opt[0][0]
return best
def recovery(self, best, option='inequality'):
"""
从QUBO解中恢复原始问题的解,并检查解的可行性。
参数:
best -- QUBO问题的最优解
option -- 指定是检查等式约束还是不等式约束
返回:
解的状态信息(最优解、可行解或不可行解)
"""
# 获取QUBO模型中的变量
vars = self.obj_ising.get_variables()
# 将最优解转换为变量值的字典
sol_dict = kw.qubo.get_sol_dict(best, vars)
# 计算目标函数的值
obj_val = kw.qubo.get_val(self.obj, sol_dict)
# 计算第一个约束条件的值
constr1_val = kw.qubo.get_val(self.constr1, sol_dict)
# 根据选项检查第二个约束条件
if option == 'equality':
constr2_flag = kw.qubo.get_val(self.constr2, sol_dict) == 0
elif option == 'inequality':
constr2_flag = True
for i in range(self.d):
for j in range(self.d):
# 检查每个位置的需求覆盖情况是否满足约束
zij_val = kw.qubo.get_val(self.z[i, j], sol_dict)
x_total_val = kw.qubo.get_val(sum(self.ALPHA[f'{i+1},{j+1}', f'{i1+1},{j1+1}'] * self.x[i1, j1]
for i1 in range(self.d) for j1 in range(self.d)), sol_dict)
if zij_val > x_total_val:
constr2_flag = False
break
# 根据约束条件的满足情况返回解的状态
if constr1_val == 0 and constr2_flag:
print('find a feasible solution')
print('obj_val', obj_val)
def main():
# 创建 CIMSolver 类的实例
solver = CIMSolver()
# 准备数据, 路径为存放数据的文件夹Data
path = 'C:/Users/admin/Desktop/try/kaiwu-sdk-enterprise/Data'
solver.prepare_data(path)
# 准备 QUBO 模型,设置惩罚系数 lambda
lam = 100 # 这个值自行设定
solver.prepare_model(lam)
# 使用模拟退火算法寻找最优解
best_solution = solver.sa()
# 从 QUBO 解中恢复原始问题的解,并检查解的可行性
solver.recovery(best_solution)
if __name__ == "__main__":
main()
第二问代码
# 定义CIMSolver类
class CIMSolver:
# 初始化数据
def prepare_data(self, path, CAP_EDGE=10):
cloud_path = os.path.join(path, 'cloud_data_within100bits.csv')
edge_path = os.path.join(path, 'edge_data_problem2_within_100bits.csv')
user_path = os.path.join(path, 'demand_data_problem2_within_100bits.csv')
# 初始化云服务器成本
C_FIX_CLOUD = {}
LOC_SET_OUTTER = []
with open(cloud_path, 'r') as f:
reader = csv.reader(f, delimiter=',', quotechar='|')
next(f)
for row in reader:
C_FIX_CLOUD[row[1] + ',' + row[2]] = int(row[3])
LOC_SET_OUTTER.append(row[1] + ',' + row[2])
self.C_FIX_CLOUD = C_FIX_CLOUD
self.LOC_SET_OUTTER = LOC_SET_OUTTER
# 初始化边缘服务器成本
C_FIX_EDGE = {}
self.LOC_EDGE = []
with open(edge_path, 'r') as f:
reader = csv.reader(f, delimiter=',', quotechar='|')
next(f)
for row in reader:
C_FIX_EDGE[row[1] + ',' + row[2]] = int(row[3])
self.LOC_EDGE.append(row[1] + ',' + row[2])
self.C_FIX_EDGE = C_FIX_EDGE
# 初始化变量成本
C_VAR_CLOUD = 1
C_VAR_EDGE = 2
self.C_VAR_CLOUD = C_VAR_CLOUD
self.C_VAR_EDGE = C_VAR_EDGE
# 初始化用户需求
DEM = {}
LOC_SET_INNER = []
LOC_SET_INNER_full = []
with open(user_path, 'r') as f:
reader = csv.reader(f, delimiter=',', quotechar='|')
next(f)
for row in reader:
LOC_SET_INNER_full.append(row[0] + ',' + row[1])
if int(row[2]):
DEM[row[0] + ',' + row[1]] = int(row[2])
LOC_SET_INNER.append(row[0] + ',' + row[1])
self.DEM = DEM
self.LOC_SET_INNER = LOC_SET_INNER
# 初始化传输成本
C_TRAN_ij = 1 # 端到边
C_TRAN_ik = 2 # 端到云
C_TRAN_jk = 1 # 边到云
self.C_TRAN_ij = C_TRAN_ij
self.C_TRAN_ik = C_TRAN_ik
self.C_TRAN_jk = C_TRAN_jk
# 全部节点
LOC_SET = LOC_SET_INNER_full + LOC_SET_OUTTER
self.LOC_SET = LOC_SET
self.num_cloud = len(self.LOC_SET_OUTTER)
self.num_edge = len(self.LOC_EDGE)
self.num_user = len(self.LOC_SET_INNER)
# 计算距离
DIST = {}
for i in LOC_SET:
for j in LOC_SET:
DIST[(i, j)] = round(np.sqrt((int(i.split(',')[0]) - int(j.split(',')[0])) ** 2 + (
int(i.split(',')[1]) - int(j.split(',')[1])) ** 2), 2)
self.DIST = DIST
# 边缘计算节点覆盖半径
RANGE = 3
self.RANGE = RANGE
# 计算覆盖关系
ALPHA = {}
for i in LOC_SET:
for j in LOC_SET:
if DIST[(i, j)] <= RANGE:
ALPHA[(i, j)] = 1
else:
ALPHA[(i, j)] = 0
self.ALPHA = ALPHA
self.CAP_EDGE = CAP_EDGE
# 准备模型
def prepare_model(self, lam_equ = None, lam = None):
# 设置等式约束的惩罚系数,默认值为[10000, 10000, 10000]
if lam_equ is None:
lam_equ = [10000, 10000, 10000]
if lam is None:
lam = [10000, 10000]
self.lam_equ = lam_equ
# 设置不等式约束的惩罚系数
self.lam = lam
# 计算每条边的最大需求
self.max_ujk = []
for j in self.LOC_EDGE:
self.max_ujk.append(sum(self.DEM * self.ALPHA[i, j] for i in self.LOC_SET_INNER))
# print('self.max_ujk', self.max_ujk)
# 初始化决策变量
self.x_edge = kw.qubo.ndarray(self.num_edge, 'x_edge', kw.qubo.binary)
self.yij = kw.qubo.ndarray((self.num_user, self.num_edge), 'yij', kw.qubo.binary)
self.yjk = kw.qubo.ndarray((self.num_edge, self.num_cloud), 'yjk', kw.qubo.binary)
self.yik = kw.qubo.ndarray((self.num_user, self.num_cloud), 'yik', kw.qubo.binary)
# 对于每条边,如果最大需求不超过边的容量,设置对应的yjk为0
for j in range(self.num_edge):
if self.max_ujk[j] <= self.CAP_EDGE:
self.yjk[j][0] = 0
# 约束2:初始化约束表达式
self.constraint2 = 0
for i in range(self.num_user):
for j in range(self.num_edge):
if self.ALPHA[(self.LOC_SET_INNER, self.LOC_EDGE[j])] == 0:
self.yij[j] = 0
else:
self.constraint2 += self.yij[j] * (1 - self.x_edge[j])
# 初始化ujk相关变量
self.ujk = np.zeros(shape=(self.num_edge, self.num_cloud), dtype=QuboExpression)
self.ujk_residual = np.zeros(shape=self.num_edge, dtype=QuboExpression)
for j in range(self.num_edge):
self.ujk_residual[j] = sum(
self.DEM[self.LOC_SET_INNER] * self.yij[j] for i in range(self.num_user)) - self.CAP_EDGE
for k in range(self.num_cloud):
self.ujk[j][k] = self.yjk[j][k] * self.ujk_residual[j]
# 目标函数
self.c_fix = sum(self.C_FIX_EDGE[self.LOC_EDGE[j]] * self.x_edge[j] for j in range(self.num_edge))
self.c_var = self.C_VAR_CLOUD * sum(sum(self.DEM[self.LOC_SET_INNER] * self.yik[k]
for i in range(self.num_user)) for k in range(self.num_cloud))
self.c_var += self.C_VAR_EDGE * sum(
sum(self.DEM[self.LOC_SET_INNER] * self.yij[j] for i in range(self.num_user))
for j in range(self.num_edge))
self.c_var += (self.C_VAR_CLOUD - self.C_VAR_EDGE) * sum(sum(self.ujk[j][k] for j in range(self.num_edge)) for k
in range(self.num_cloud))
self.c_tran = self.C_TRAN_ij * sum(
sum(self.DEM[self.LOC_SET_INNER] * self.DIST[(self.LOC_SET_INNER, self.LOC_EDGE[j])] * self.yij[j]
for i in range(self.num_user)) for j in range(self.num_edge))
self.c_tran += self.C_TRAN_ik * sum(sum(
self.DEM[self.LOC_SET_INNER] * self.DIST[(self.LOC_SET_INNER, self.LOC_SET_OUTTER[k])] * self.yik[k]
for i in range(self.num_user)) for k in range(self.num_cloud))
self.c_tran += self.C_TRAN_jk * sum(sum(self.DIST[(self.LOC_EDGE[j], self.LOC_SET_OUTTER[k])] * self.ujk[j][k]
for j in range(self.num_edge)) for k in range(self.num_cloud))
self.obj = self.c_fix + self.c_var + self.c_tran
# 约束1:确保每个用户的服务需求仅被分配到一个位置(边侧或云侧)
self.constraint1 = 0
for i in range(self.num_user):
self.constraint1 += (sum(self.yij[j] for j in range(self.num_edge))
+ sum(self.yik[k] for k in range(self.num_cloud)) - 1) ** 2
# 不等式约束1:需求减去边的最大容量后,应该满足yjk约束
self.ineq_constraint1 = []
self.ineq_qubo1 = 0
self.len_slack1 = math.ceil(math.log2(max(self.max_ujk) + 1))
self.slack1 = kw.qubo.ndarray((self.num_edge, self.num_cloud, self.len_slack1), 'slack1', kw.qubo.binary)
for j in range(self.num_edge):
self.ineq_constraint1.append([])
for k in range(self.num_cloud):
if self.yjk[j][k] == 0:
self.ineq_constraint1[j].append(0)
else:
self.ineq_constraint1[j].append(
self.ujk_residual[j] - (self.max_ujk[j] - self.CAP_EDGE) * self.yjk[j][k])
self.ineq_qubo1 += (self.ineq_constraint1[j][k] + sum(
self.slack1[j][k][_] * (2 ** _) for _ in range(self.len_slack1))) ** 2
# 不等式约束2:边的容量应大于等于需求
self.ineq_qubo2 = 0
self.ineq_constraint2 = []
self.len_slack2 = math.ceil(math.log2(max(self.max_ujk) + 1))
self.slack2 = kw.qubo.ndarray((self.num_edge, self.num_cloud, self.len_slack2), 'slack2', kw.qubo.binary)
for j in range(self.num_edge):
self.ineq_constraint2.append([])
for k in range(self.num_cloud):
if self.yjk[j][k] == 0:
self.ineq_constraint2[j].append(0)
else:
self.ineq_constraint2[j].append(self.yjk[j][k] * self.CAP_EDGE -
sum(self.DEM[self.LOC_SET_INNER] * self.yij[j] for i in
range(self.num_user)))
self.ineq_qubo2 += (self.ineq_constraint2[j][k] + sum(self.slack2[j][k][_] * (2 ** _)
for _ in range(self.len_slack2))) ** 2
# 约束3:确保yjk与x_edge之间的关系
self.constraint3 = 0
for j in range(self.num_edge):
for k in range(self.num_cloud):
self.constraint3 += self.yjk[j][k] * (1 - self.x_edge[j])
# 构建最终模型
self.model = self.obj
self.model += self.lam_equ[0] * self.constraint1 + self.lam_equ[1] * self.constraint2 \
+ self.lam_equ[2] * self.constraint3
self.model += self.lam[0] * self.ineq_qubo1 + self.lam[1] * self.ineq_qubo2
# 将模型转换为Ising模型
Q = self.model
Q = kw.qubo.make(Q)
ci = kw.qubo.cim_ising_model(Q)
self.obj_ising = ci
ising = ci.get_ising()
self.matrix = ising["ising"]
bias = ising["bias"]
def sa(self, max_iter, ss = None, T_init = 1000, alpha = 0.99, T_min = 0.0001, iterations_per_T = 10):
"""
执行模拟退火算法来寻找问题的最优解。
参数:
- max_iter: 最大迭代次数
- T_init: 初始温度
- alpha: 温度衰减系数
- T_min: 最低温度
- iter_per_t: 每个温度下的迭代次数
- size_limit: 解的大小限制
"""
iter = 0
current_best = math.inf # 初始化当前最佳解为无穷大
opt_obj = 0 # 期望的最优目标值(可以根据具体问题调整)
init_solution = None # 初始化解
while (iter < max_iter and current_best > opt_obj):
print(f'第 {iter} 次迭代开始,当前最佳解 = {current_best}')
# print('当前最佳解 = ', current_best)
# 执行模拟退火算法
output = kw.classical.simulated_annealing(
self.matrix,
s=ss,
T_init=T_init,
alpha=alpha,
T_min=T_min,
iterations_per_T=iterations_per_T)
# 从模拟退火输出中获取最优解
opt = kw.sampler.optimal_sampler(self.matrix, output, bias=0, negtail_ff=True)
for vec in opt[0]:
# 恢复解并计算目标值
flag, val_obj = self.recovery(vec)
if flag:
# print('可行解,目标值:', val_obj)
current_best = min(current_best, val_obj) # 更新当前最佳解
iter += 1
# print(self.recovery(opt[0][0]))
print('最优解:', current_best)
def recovery(self, best):
"""
恢复最优解并计算约束条件和目标值。
参数:
- best: 最优解向量
返回:
- (flag, val_obj): flag表示解是否可行,val_obj是目标值或不等式违反的数量
"""
vars = self.obj_ising.get_variables() # 获取变量集合
sol_dict = kw.qubo.get_sol_dict(best, vars) # 获取解的字典表示
self.val_eq1 = kw.qubo.get_val(self.constraint1, sol_dict) # 计算约束1的值
self.val_eq2 = kw.qubo.get_val(self.constraint2, sol_dict) # 计算约束2的值
self.val_eq3 = kw.qubo.get_val(self.constraint3, sol_dict) # 计算约束3的值
num_ineq_vio = 0 # 不等式违反数量计数器
Flag = True # 标记解是否可行
# 检查等式约束
if self.val_eq1 + self.val_eq2 + self.val_eq3:
Flag = False
# 检查不等式约束1
for j in range(self.num_edge):
for k in range(self.num_cloud):
if self.ineq_constraint1[j][k] != 0 and kw.qubo.get_val(self.ineq_constraint1[j][k], sol_dict) > 0:
Flag = False
num_ineq_vio += 1
# 检查不等式约束2
for j in range(self.num_edge):
for k in range(self.num_cloud):
if self.ineq_constraint2[j][k] != 0 and kw.qubo.get_val(self.ineq_constraint2[j][k], sol_dict) > 0:
Flag = False
num_ineq_vio += 1
# 返回结果:如果解可行,返回目标值,否则返回不等式违反数量
return (True, kw.qubo.get_val(self.obj, sol_dict)) if Flag else (False, num_ineq_vio)
def main():
# 创建 CIMSolver 类的实例
solver = CIMSolver()
# 准备数据, 路径为存放数据的文件夹Data
path = 'C:/Users/admin/Desktop/try/kaiwu-sdk-enterprise/Data'
solver.prepare_data(path)
# 准备 QUBO 模型,设置惩罚系数 lambda
solver.prepare_model()
# 使用模拟退火算法寻找最优解
max_iter = 100
solver.sa(max_iter)
if __name__ == "__main__":
main()
|












