本帖最后由 Akkio 于 2026-1-16 02:47 编辑
本文衔接生成式模型基础,聚焦随机量子化与扩散模型的核心关联及机制。随机量子化通过引入虚构时间与Langevin方程,使量子场经布朗运动收敛至路径积分权重对应的平衡分布,Fokker-Planck方程验证了该平衡态的稳定性。扩散模型则通过正向加噪、反向去噪过程生成样本,其核心与随机量子化深度对接,Score函数对应Langevin方程中的有效力场,本质是概率分布的对数梯度。因正向加噪后分布难以解析,需通过神经网络学习Score函数,为扩散模型在格点场论采样中的应用奠定物理与理论基础。
上一篇:物理学家用扩散模型(一):生成式模型基础——KL 散度理论与格点场论采样需求
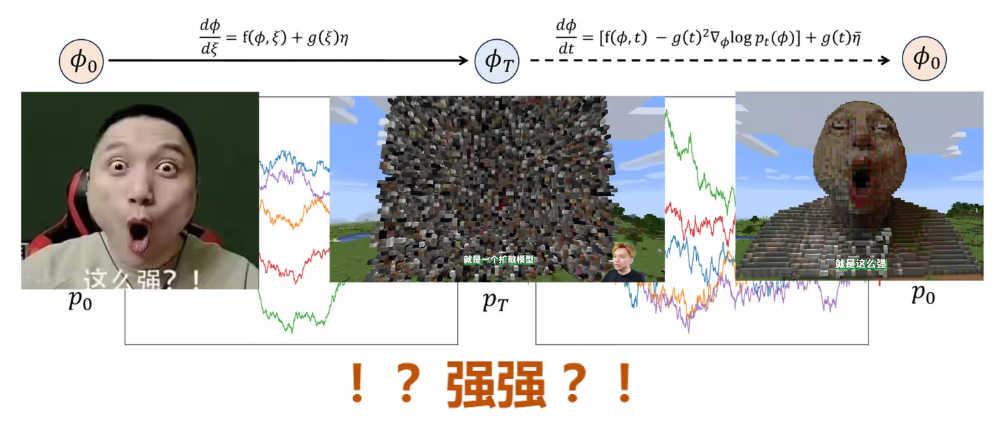
3.1 基础铺垫:随机量子化
3.1.1 核心思想
Parisi和吴咏时1981年提出随机量子化,为格点量子场论提供重要工具。其核心是引入虚构时间τ(Langevin时间),让量子场在该时间上做布朗运动,最终达到的平衡分布恰好等价于量子场论的路径积分权重。
3.1.2 Langevin方程与平衡分布
Langevin方程:
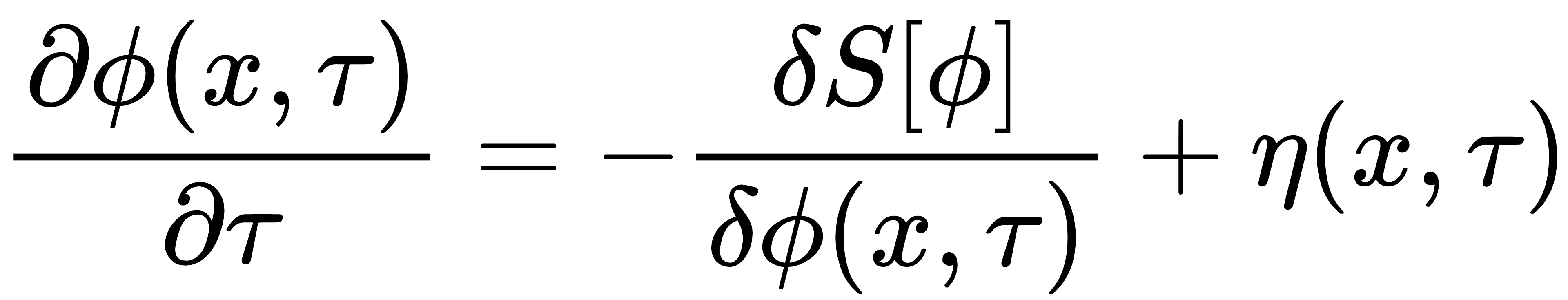
其中,漂移项使系统沿作用量负梯度下降,趋于最小作用量;噪声项保证遍历所有场构型,满足 。 。
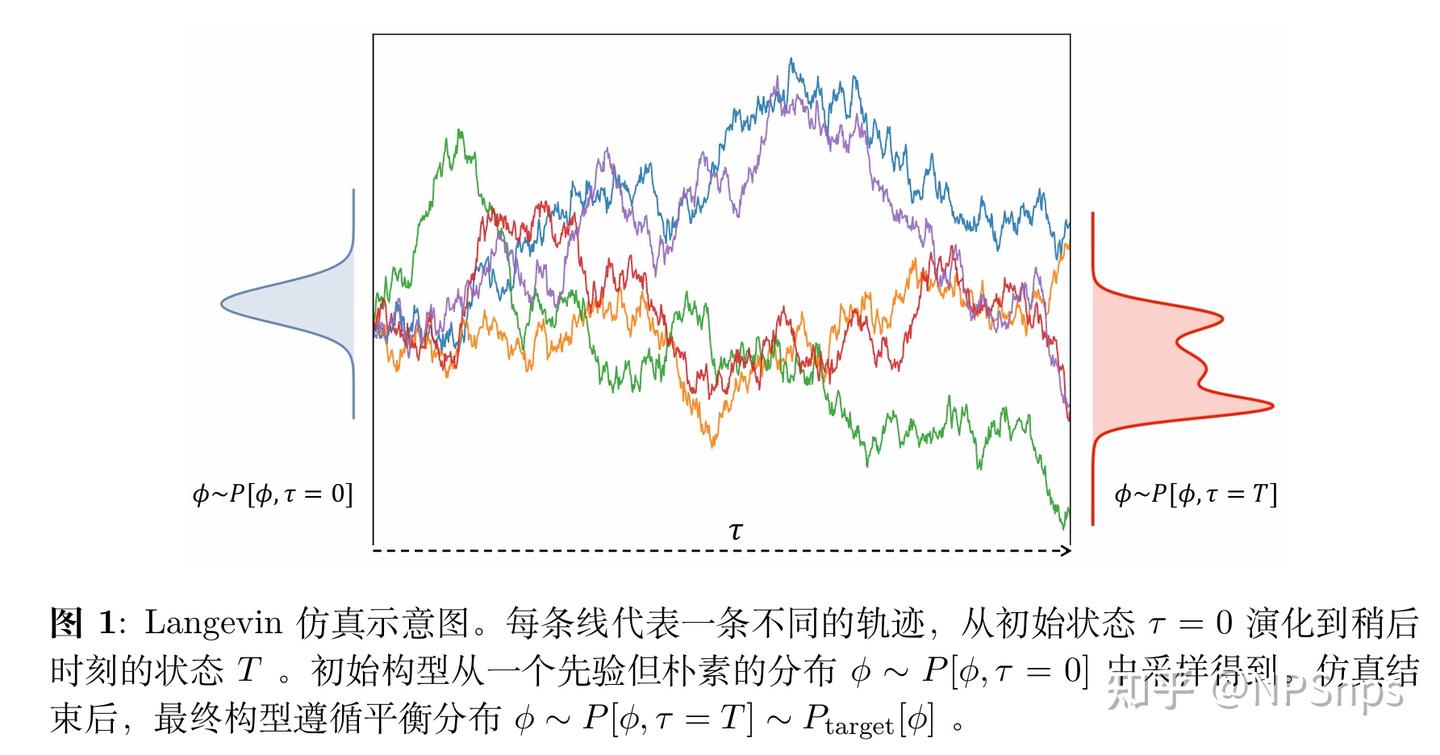
平衡分布:当τ→∞时,Langevin动力学达到平衡分布,量子涨落由噪声产生,作用量驱动系统向“量子平衡”收敛,这是随机量子化等价于传统路径积分的核心原因。
3.1.3 Fokker-Planck方程
Langevin随机微分方程(SDE)对应的概率密度满足Fokker-Planck方程,以一维情况为例:
一维Langevin方程:
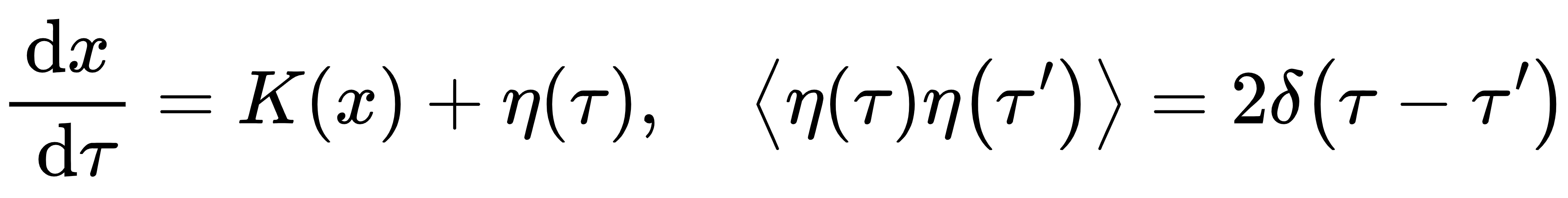
小步长Δτ下的离散形式:( 为标准正态分布变量)
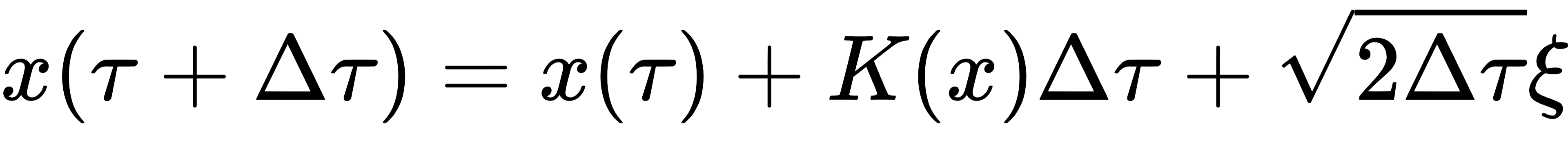
其中,ε服从标准正态分布变量
将 Langevin 方程在一个小步长Δτ上积分
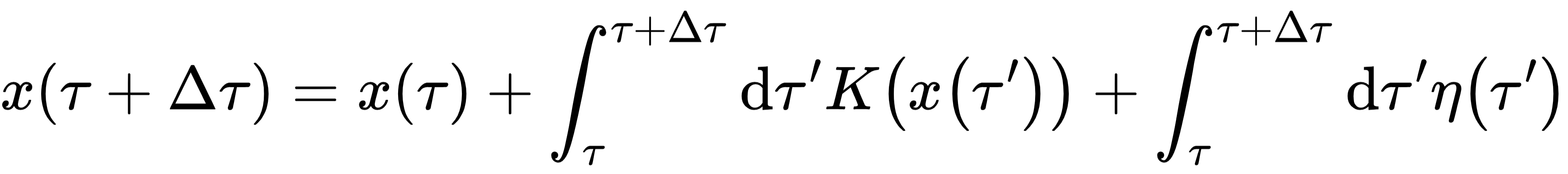
定义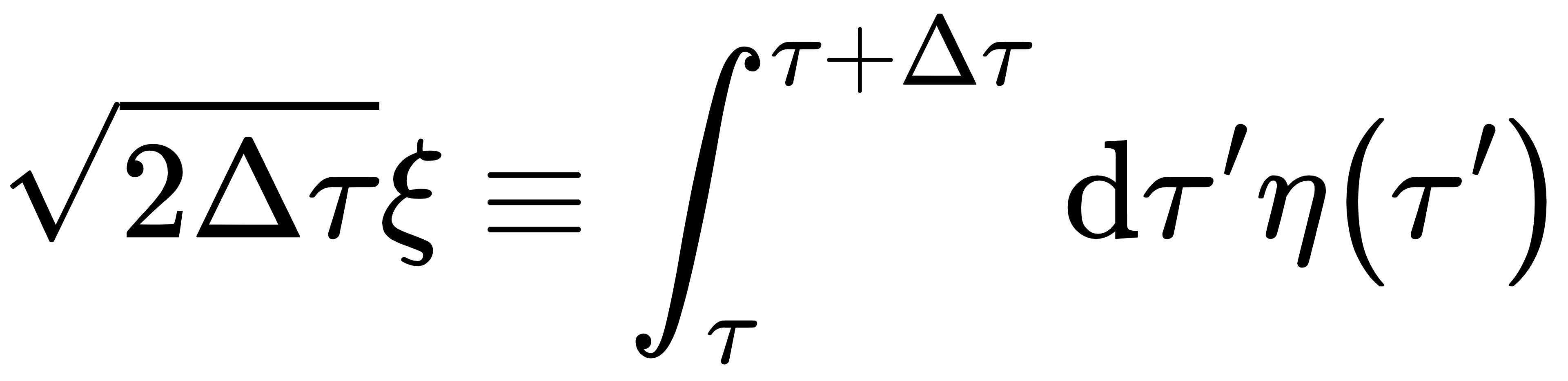 ,其统计性质有 ,其统计性质有
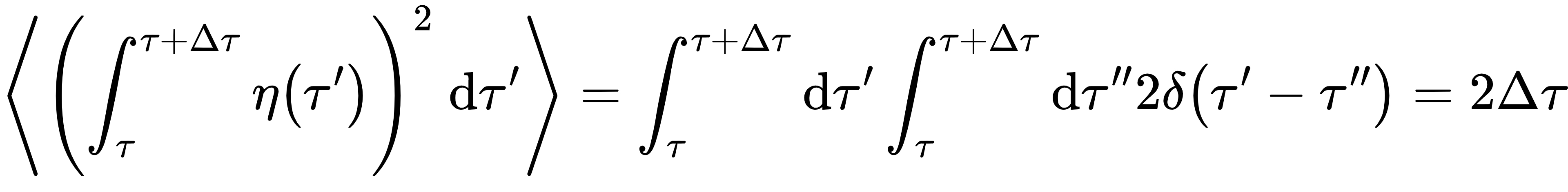
因此 ,ε是标准正态分布变量
Fokker-Planck方程:
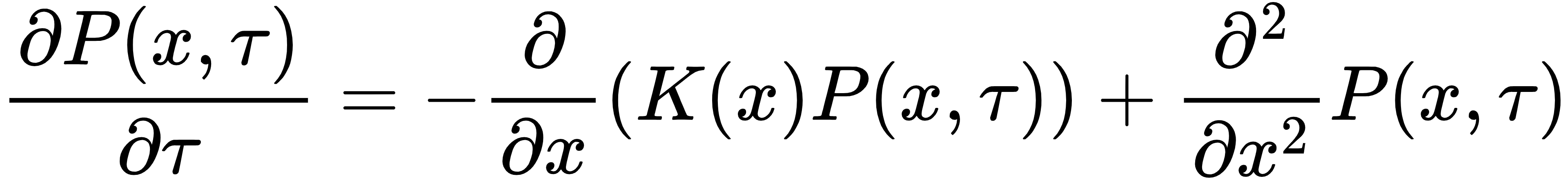
场论推广:将一维情况推广到场变量,Langevin方程变为 :

3.1.4 Langevin时间演化的稳定性验证
当τ→∞时,存在稳定平衡态Peq[Φ]满足∂τPeq=0 。物理直觉上,这是“热浴+力”的平衡:Φ为粒子坐标,S[Φ]为粒子势能,η为温度T=1的热浴,τ为真实时间,Langevin动力学长期行为必然是玻尔兹曼分布。
验证:将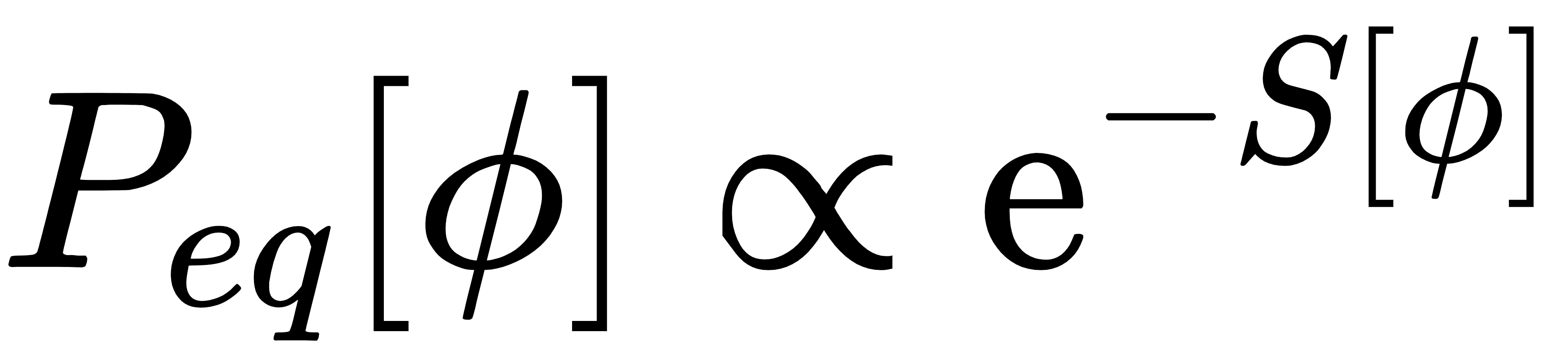 代入Fokker-Planck方程,可得: 代入Fokker-Planck方程,可得:
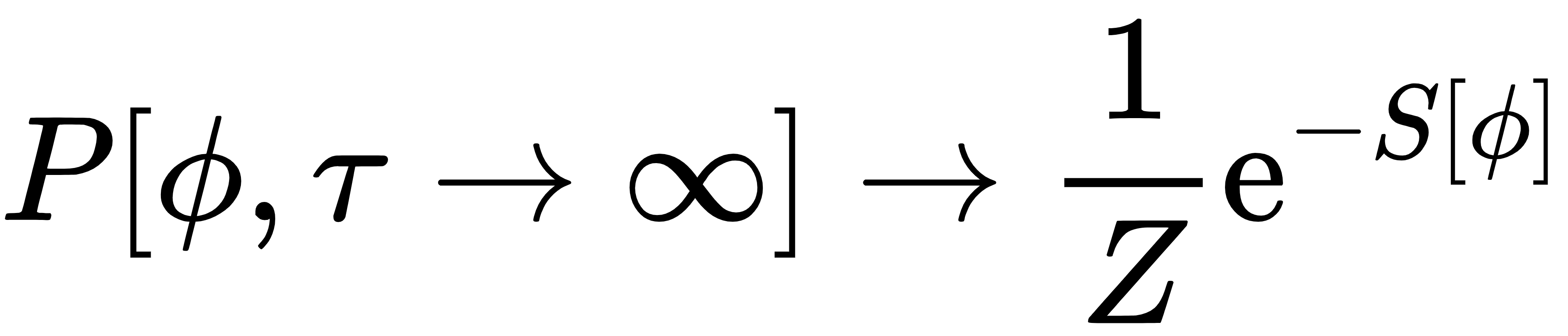
即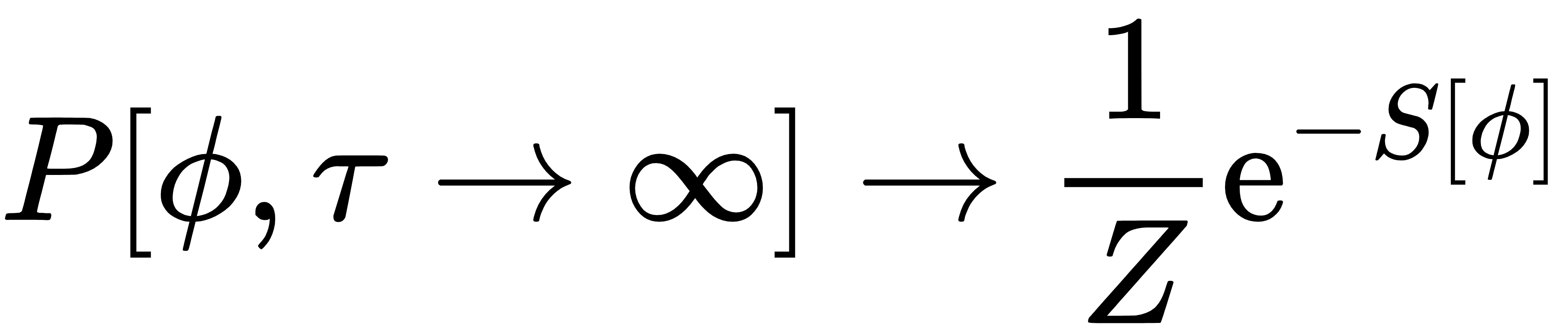 ,验证了平衡分布的正确性。 ,验证了平衡分布的正确性。
3.2 Diffusion Model的核心机制
3.2.1 与随机量子化的对接
随机量子化是真实的动力学微分方程演化,Diffusion Model是学习出来的概率生成器。
随机量子化:解真实的随机微分方程(SDE),依赖 ,每一步具有明确物理意义。
Diffusion Model:学习反向生成过程,仅需样本,中间步骤为计算工具,核心是学习“有效Langevin力”。
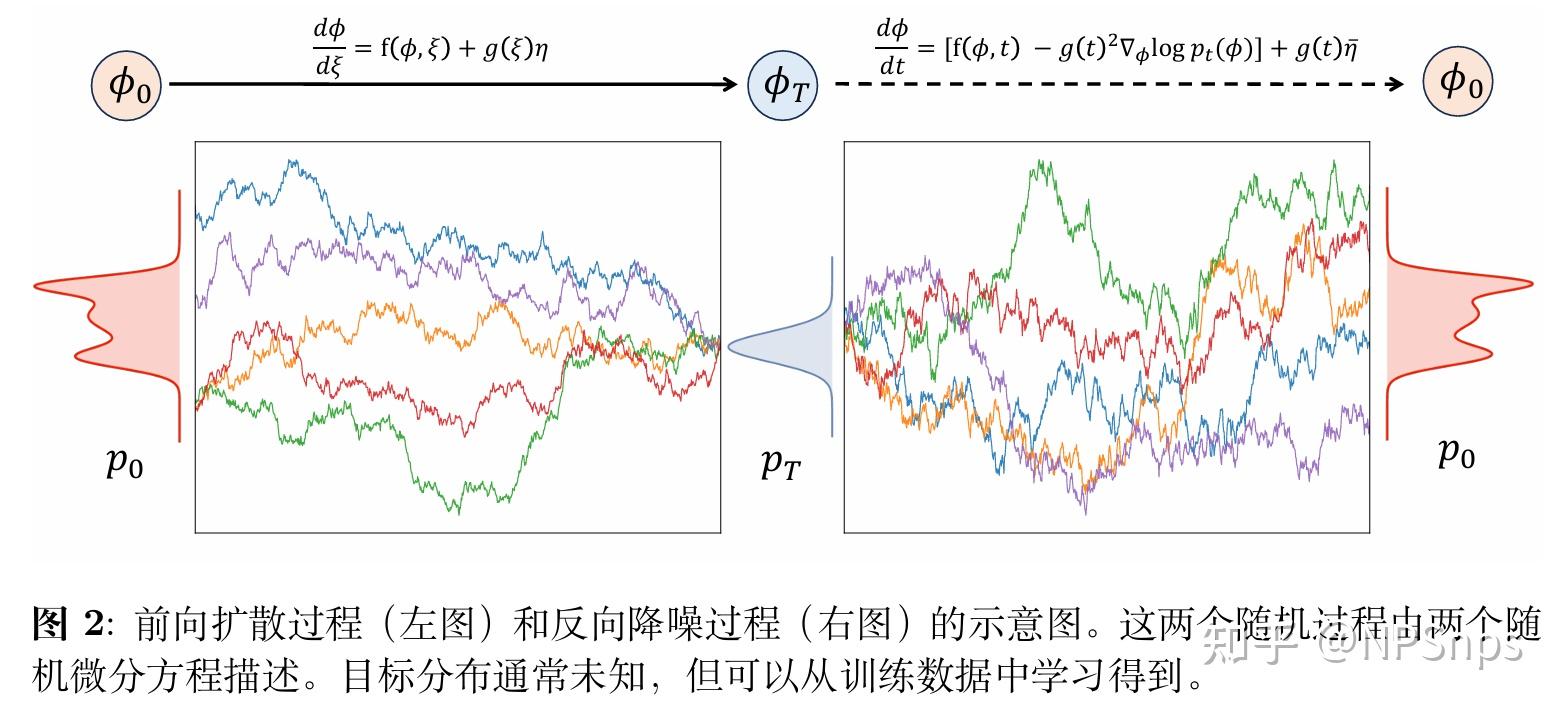
3.2.2 核心思想:正向过程与反向过程
正向扩散过程(Forward process):人为定义的加噪过程,从真实分布p0(Φ)出发,不断加入噪声(ξ为噪声变量,随时间衰减的系数αt∈(0,1)用于控制每步的噪声大小),使分布逐渐平坦:
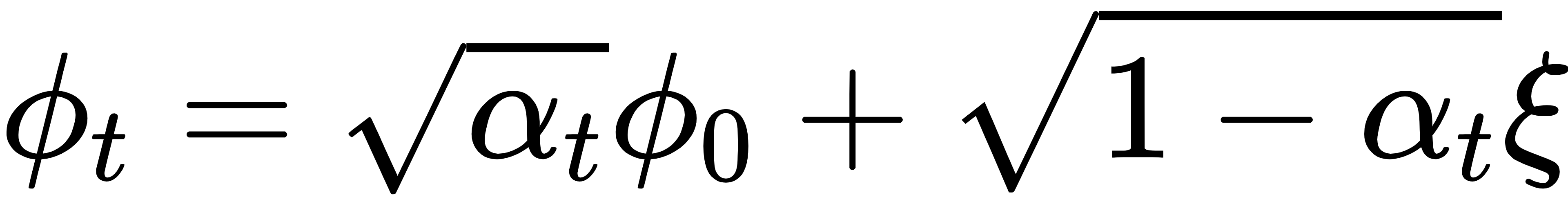
反向扩散过程(Reverse process):机器学习的核心,理论上存在反向SDE:
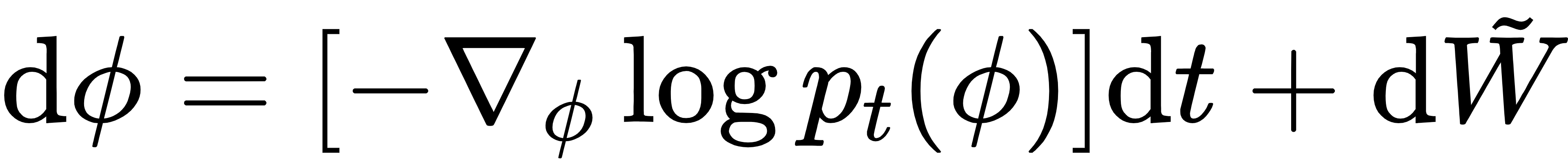
Diffusion Model 用神经网络学习score函数 ,再从高斯噪声出发,通过反向SDE生成样本。 ,再从高斯噪声出发,通过反向SDE生成样本。
3.2.3 Score函数的物理意义
定义:对概率密度p(x),score函数为概率密度对变量的对数梯度:score(x)=▽x log p(x),该梯度指向概率更大的方向。
与随机量子化的关联:在随机量子化中,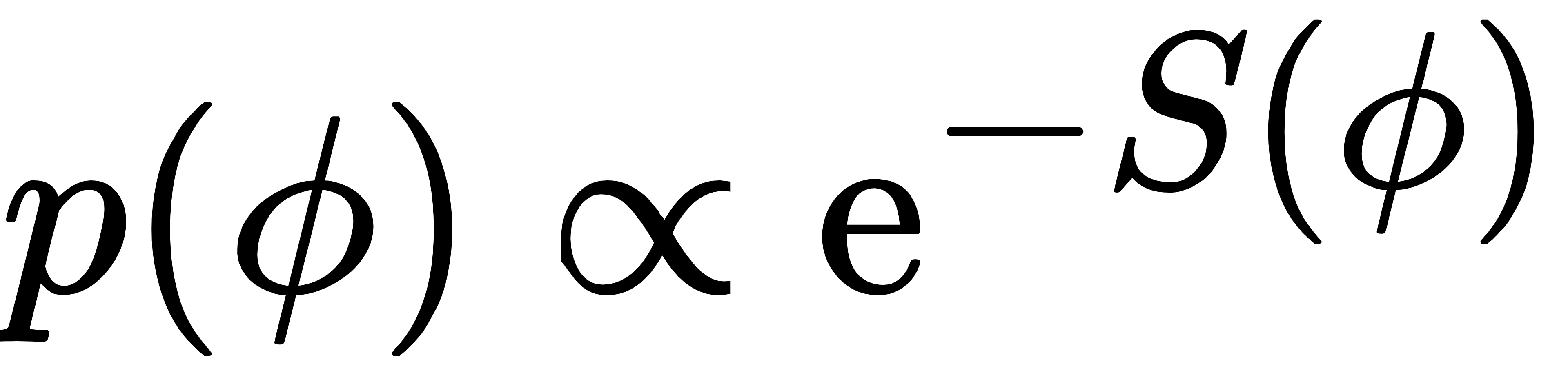 ,因此 ,因此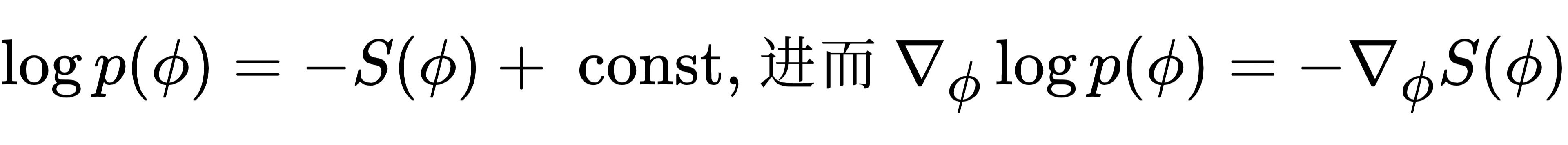 ,即score函数等于“负的作用量梯度”,恰好是Langevin方程中的力。 ,即score函数等于“负的作用量梯度”,恰好是Langevin方程中的力。
回顾 Langevin SDE,Langevin 就是沿着 score 方向漂移,再加噪声
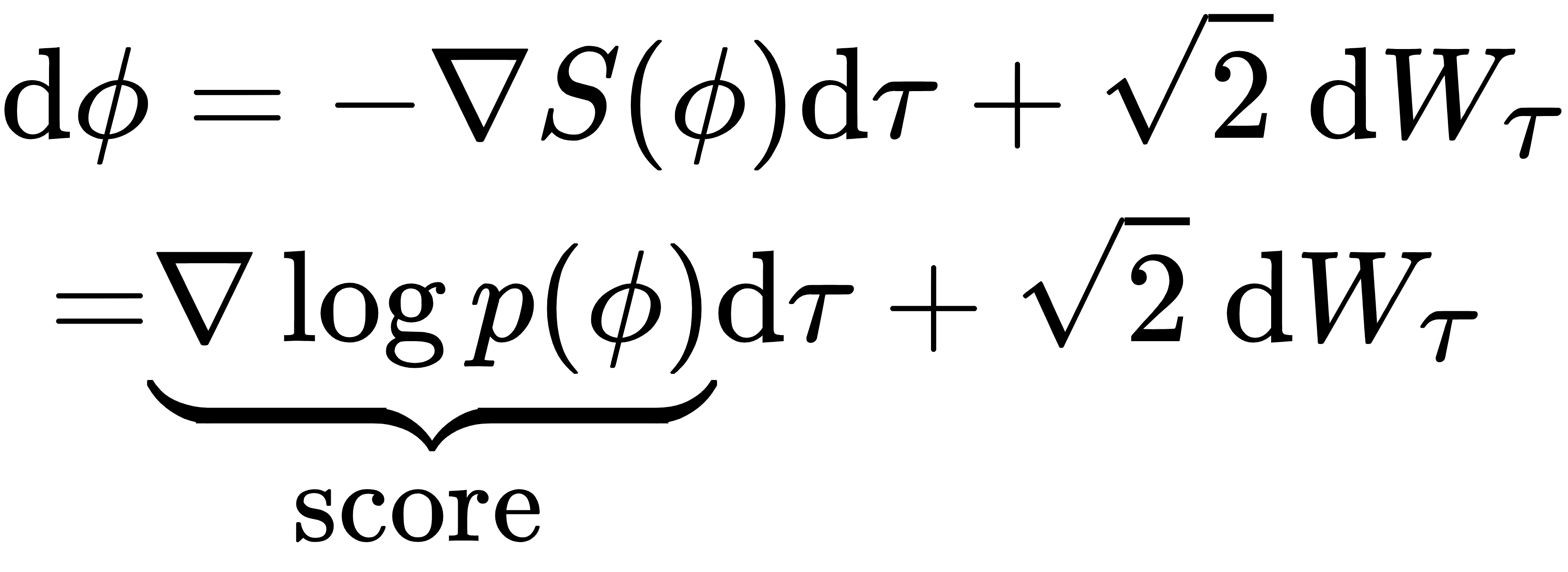
score 函数是“概率分布在构型空间中的力场”,在随机量子化中,它是-δS/δΦ,在 Diffusion Model 中,它是被神经网络学习出来的。
3.2.4 Score函数的学习必要性与获取方式
权重函数 ,因高维、非线性强耦合、拓扑扇区分离等问题不可直接求解。Langevin方法虽仅需当前 ,但存在自关联时间长、隧穿慢、临界减速等缺陷。 ,因高维、非线性强耦合、拓扑扇区分离等问题不可直接求解。Langevin方法虽仅需当前 ,但存在自关联时间长、隧穿慢、临界减速等缺陷。
在t=0处,若作用量S可算,则目标分布处p0(x)和score 函数已知。但在t≠0处,Forward diffusion重新定义了分布
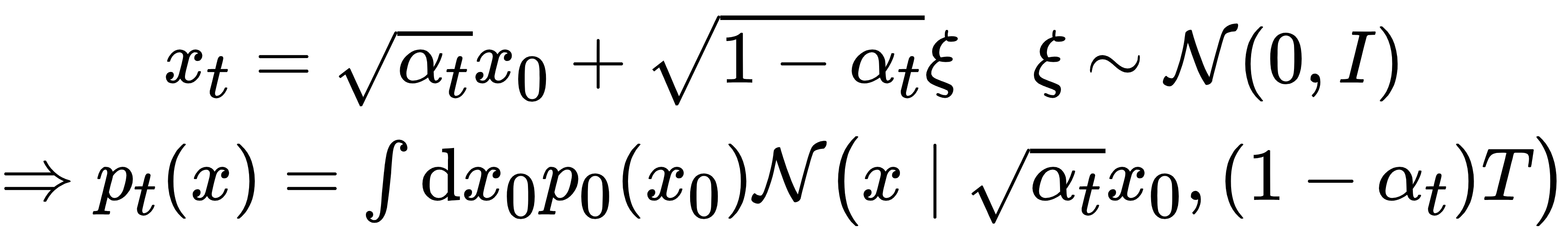
因此在Diffusion Model中,正向扩散后的分布pt(x)是卷积后的分布,难以写出解析形式,score函数的分子、分母均为高维积分,计算成本极高,因此必须通过神经网络学习。

Diffusion Model中,需要获得score函数: Forward diffusion 中人为加噪声,pt(x)变得越来越平;Reverse diffusion 为了生成样本,需要解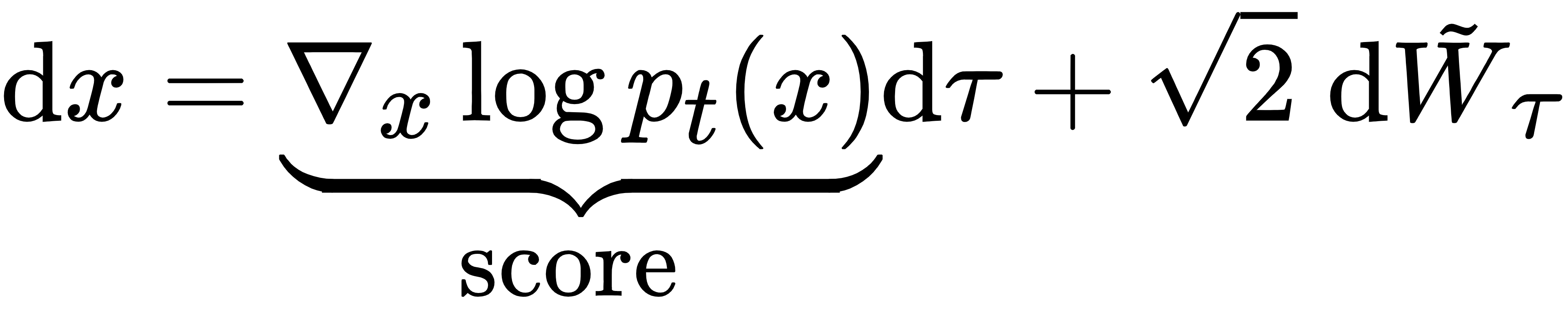 。但正向扩散的每一步的分布pt(x)是无法直接计算的(因为是加噪后的复杂分布),所以也不知道score 函数。解决办法是:用神经网络学习 score 函数—— 训练一个带参数θ的网络sθ(x,t),让它近似等于真实的 score 函数。 。但正向扩散的每一步的分布pt(x)是无法直接计算的(因为是加噪后的复杂分布),所以也不知道score 函数。解决办法是:用神经网络学习 score 函数—— 训练一个带参数θ的网络sθ(x,t),让它近似等于真实的 score 函数。

文章改编转载自知乎作者:NPSnps
原文链接:https://zhuanlan.zhihu.com/p/1993278533036963266 | 











