本帖最后由 Akkio 于 2026-1-22 01:16 编辑
上一篇:物理学家用扩散模型(二):随机量子化+Score函数=扩散模型
3.3 正向与反向扩散的数学基础:Anderson定理
Anderson定理揭示了正向与反向SDE的关系:
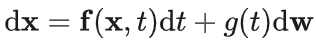
正向扩散SDE:对应的Fokker-Planck方程(前向Kolmogorov方程,KFE):
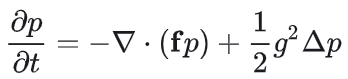
反向生成扩散SDE:取时间逆转dt-=-dt,设反向SDE(Reverse-Time SDE)为
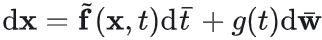
则反向Fokker-Planck方程(后向Kolmogorov方程,KBE)为:
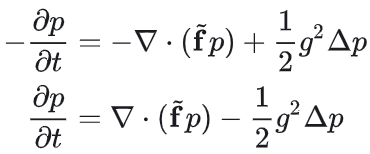
由于KFE与KBE都描述了同一-p(x,t)在正、反时间下的演化率,因此有
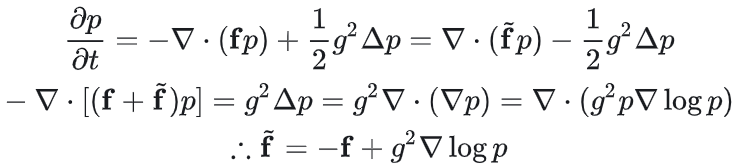
此即 Anderson (1982) 论文中的结论,因此反向SDE为:
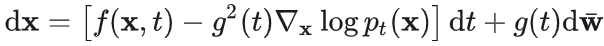
3.4 从噪声生成目标分布的具体过程
3.4.1 反向生成 SDE
忽略正向漂移项f(Φ,t),反向SDE简化为:
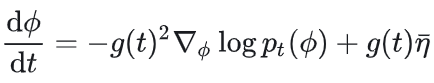
定义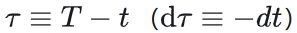 ,则: ,则:
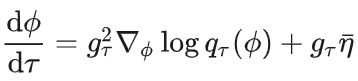
离散化后:
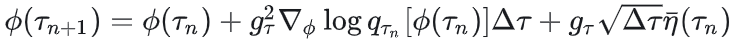
其中噪声尺度满足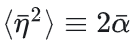 ,时间尺度为 ,时间尺度为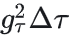 。 。
3.4.2 对应的Fokker-Planck方程与平衡分布
反向SDE对应的Fokker-Planck方程:
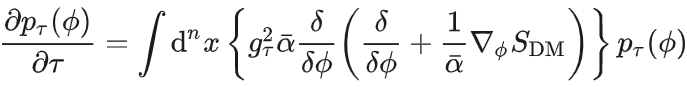
其中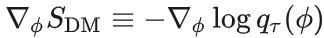 。当τ→T时,平衡分布 。当τ→T时,平衡分布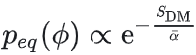 ,最终收敛到目标分布 ,最终收敛到目标分布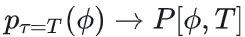 。 。
3.4.3 核心特点
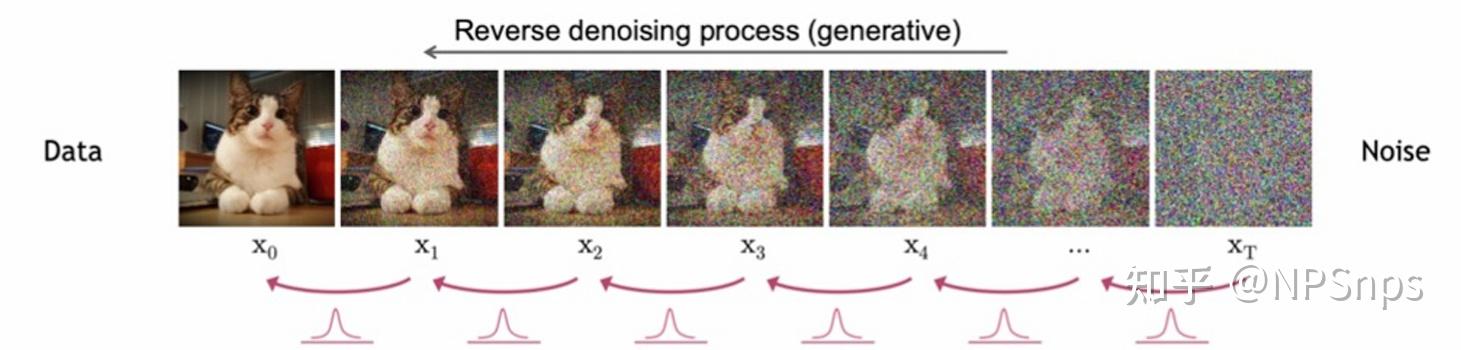
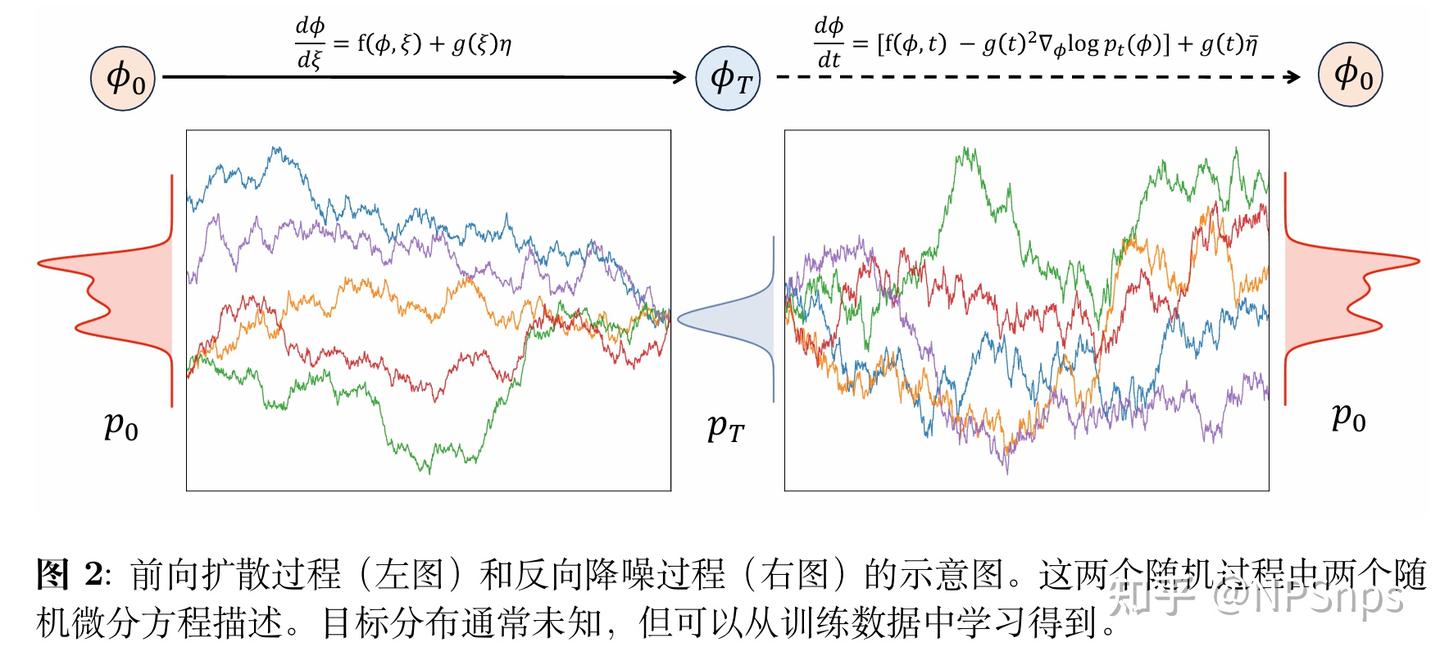
在已知 “正向加噪扩散” 的前提下,反向过程是 “从纯噪声逐步去噪、最终生成真实样本” 的概率分布层面过程,而非 “正向的逆轨迹”:
· 正向扩散是 “无条件、无记忆” 的加噪过程,单条轨迹无法倒推;
· 反向扩散是 “概率分布层面” 的演化:score 函数提供 “概率力场”,在每个噪声尺度下,将构型往 “真实样本所在的高概率区域” 拉回。
score 函数并非直接学习作用量S(x),而是学习 “典型构型附近ΔS(x)的形式。
· Langevin/HMC:依赖完整的势能函数,每一步沿 “本地梯度” 演化;
· Diffusion/score:不重建全局分布,仅在 “常被访问的高概率区域” 学习 “高效路径”,快速覆盖真实样本区域。
Diffusion Model 学习的 score 函数是近似、全局的力sθ(x)~∇S(x)。
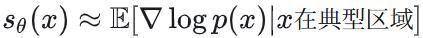 ,在物理上等价于积掉高频自由度后的有效力。不同时间下的有效作用量在改变,类似于粗粒化重整化群流。 ,在物理上等价于积掉高频自由度后的有效力。不同时间下的有效作用量在改变,类似于粗粒化重整化群流。
最后,反向过程生成的样本需通过Metropolis Hastings 接受 - 拒绝步骤,确保最终分布严格匹配目标分布。
下一篇:物理学家用扩散模型(四):Score Matching + 加噪=NCSN
文章改编转载自知乎作者:NPSnps
原文链接:https://zhuanlan.zhihu.com/p/1993655834497003850 | 











