本帖最后由 Akkio 于 2026-1-22 01:24 编辑
上一篇:物理学家用扩散模型(三):反向SDE从噪声生成目标分布
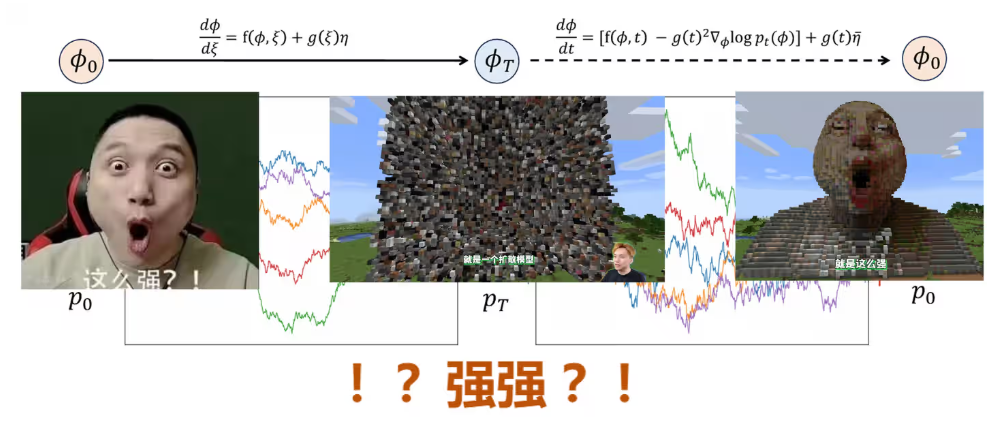
3.5 Score Matching
3.5.1 Fisher散度与训练目标
引入Fisher散度衡量真实分布与模型分布的差异:
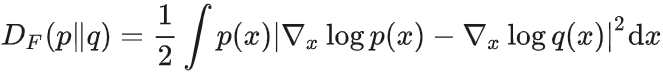
对比正向KL散度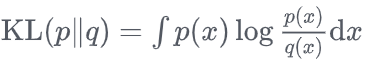 可知 Fisher 散度是Forward型、但比较的是log密度的梯度。 可知 Fisher 散度是Forward型、但比较的是log密度的梯度。
最小化Fisher散度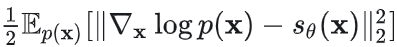 等价于训练score函数。 等价于训练score函数。
对于一维情形:
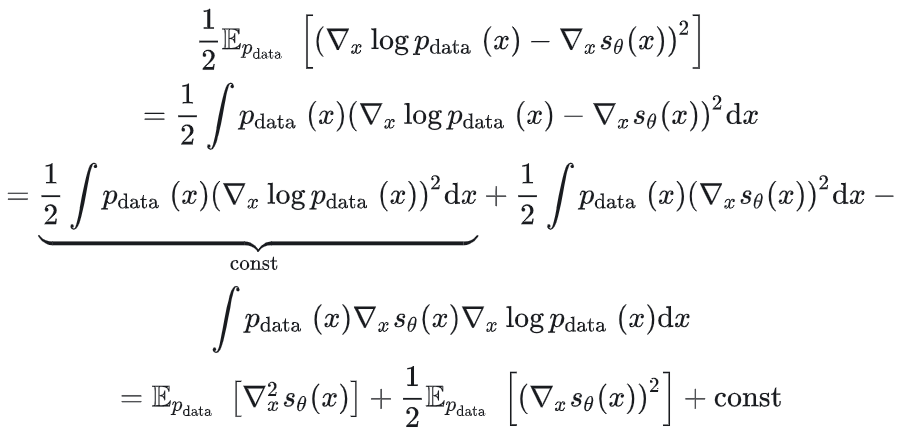
其中分部积分
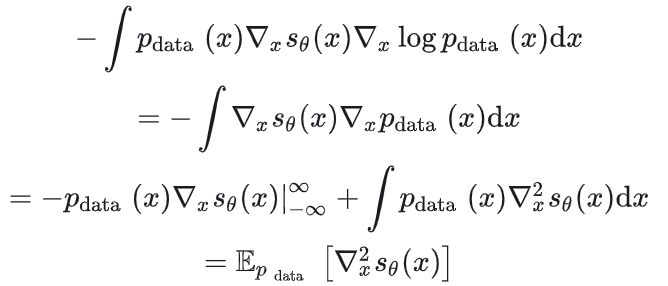
对于多变量,则是最小化
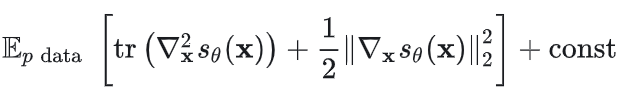
因此最小化 Fisher 散度等价于
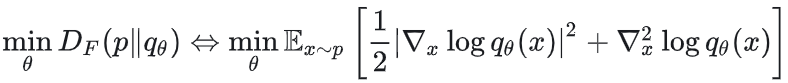
3.5.2 二阶梯度的计算
对于大多数神经网络,一阶梯度项可以用反向传播直接算,成本是和前向传播同量级
前向传播:输入数据x经层f1,f2,...,fL得到输出^y=fL○...○f1(x)记录每层输出以计算损失;
反向传播:通过损失L对第i层权重Wi的变化率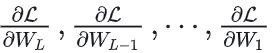 调整网络权重。 调整网络权重。
而对于二阶梯度项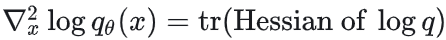 ,出现了Hessian矩阵的迹,在x维度高时(如场论)下存在问题: ,出现了Hessian矩阵的迹,在x维度高时(如场论)下存在问题:
计算成本极高:Hessian是大型矩阵,迹需访问所有对角元;
自动微分框架限制:自动微分的反向传播天然是输出对中间变量和参数的一阶梯度,而 Hessian元素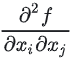 需额外计算,且自动微分框架无法仅算对角线,前向+反向传播计算梯度的过程会涉及到所有节点。 需额外计算,且自动微分框架无法仅算对角线,前向+反向传播计算梯度的过程会涉及到所有节点。
解决方案(噪声条件得分网络,NCSN):对数据加高斯噪声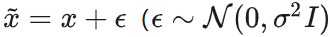 ,得到平滑分布 ,得到平滑分布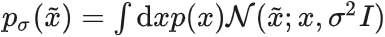 ,考虑采用加噪版本的Fisher散度: ,考虑采用加噪版本的Fisher散度:
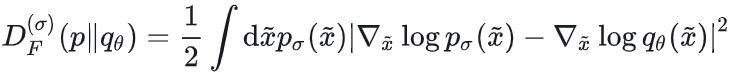
有关键恒等式:
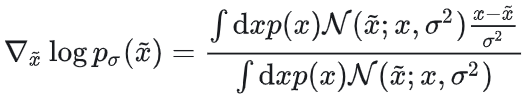
给定~x时,score指向“最可能生成~x的干净样本 ”的方向,尽管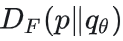 与 与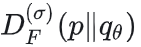 数值上不相等,但若模型足够强,则 数值上不相等,但若模型足够强,则
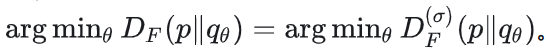

3.5.3 显式分数匹配与降噪分数匹配
显式分数匹配 Explicit Score Matching(ESM,SM)定义:
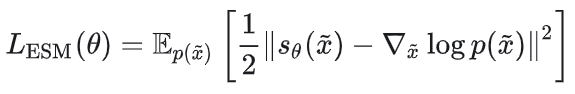
降噪分数匹配 Denoising Score Matching(DSM)定义:
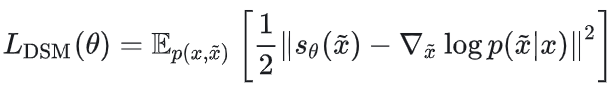
可证明定理:
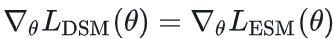
即两种训练方法的梯度等价。
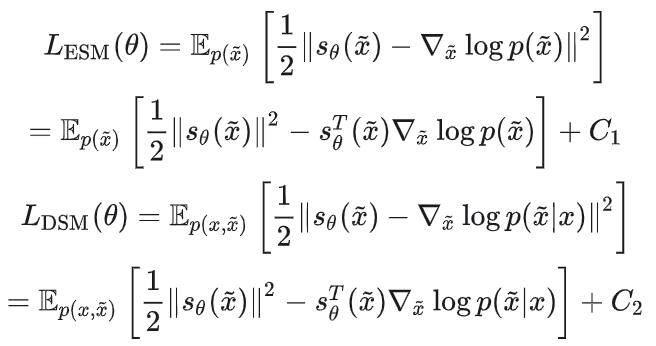
因此只要证明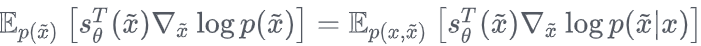 ,而 ,而
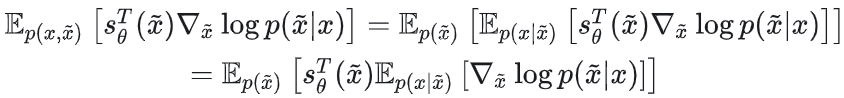
因此只要证明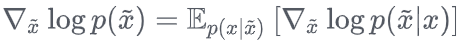 ,展开可得 ,展开可得
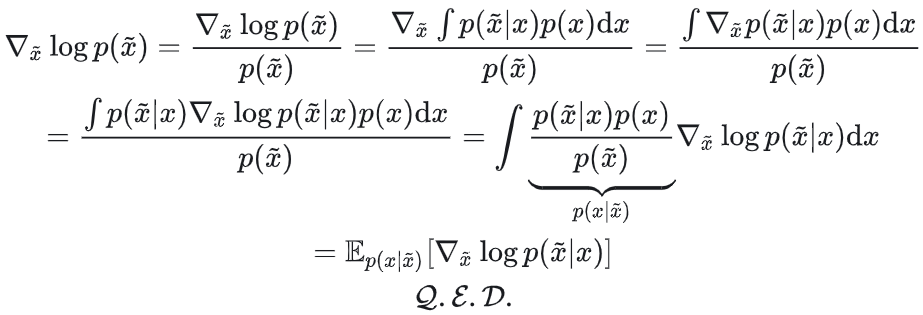
3.5.4 实际计算中的近似
高斯噪声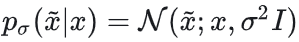 ,则 ,则
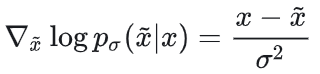
联合分布积分有
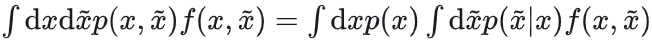
期望近似:
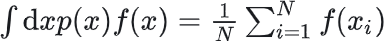
(其中xi~p(x),通过随机抽样估算期望)
3.6 Diffusion Model与传统采样的核心差异
样本≠生成机制 Diffusion Model 学的不是“已有样本”,而是一个可泛化、可条件化、可加速的 生成动力学。
样本只是被动数据 不能重新加权、快速生成独立样本、改变概率分布参数。
样本≠概率分布 传统方法仅能获取样本,无法知晓概率分布解析形式;而 Diffusion Model 学习从噪声生成数据的过程,间接逼近概率分布。
Diffusion≠复刻已有样本 可从噪声生成无限新样本,生成样本之间的相关性可控,可用作proposal distribution,可替代或加速蒙特卡洛采样。
文章改编转载自知乎作者:NPSnps
原文链接:https://zhuanlan.zhihu.com/p/1993827238261577588 | 











