本帖最后由 graphite 于 2026-1-26 18:59 编辑
PsiQuantum 与空客团队提出扩展型量子格子玻尔兹曼算法,通过卡尔曼嵌入将非线性流体方程线性化,首次融入壁面、进出口、外力等真实边界条件。实验验证显示,该算法在Nc=2时,圆柱绕流相对误差从 7% 降至 2.5%,顶盖驱动方腔流能准确复现回流结构,条件数随 Re 弱缩放保持量子优势。其量子门复杂度额外开销为O(4Nc),辅助比特数线性增长,为复杂流动的量子模拟提供了工程可行的框架。

计算流体动力学(CFD)是航空航天、海洋工程等领域的核心工具,但传统模拟面临 “高雷诺数下计算复杂度爆炸”“复杂边界条件难适配” 的困境。PsiQuantum 与空客团队联合在预印本发表研究,提出扩展型量子格子玻尔兹曼算法,通过卡尔曼嵌入(Carleman Embedding)将非线性流体动力学方程转化为高维线性系统,首次融入壁面、进出口、外力等真实边界条件,在保持量子优势渐近缩放的同时,实现对驱动泰勒 - 格林涡、顶盖驱动方腔流、圆柱绕流等典型流动的精准模拟,为量子 CFD 走向工程应用铺平道路。
一、传统流体模拟的 “算力天花板”
流体流动遵循非线性的纳维 - 斯托克斯方程,传统 CFD 模拟(如有限体积法、谱元法)面临两大核心瓶颈:
非线性难解:方程中的对流项(u⋅∇u)导致非线性耦合,经典计算机需通过大量网格离散逼近求解,计算复杂度随雷诺数(Re)立方增长;
边界条件适配难:真实场景中的壁面无滑移、进出口自由流等非周期性边界,会大幅增加经典算法的通信开销与代码复杂度;
算力需求巨大:模拟高雷诺数湍流或复杂几何绕流(如飞机起落架、风力机),即使超级计算机也需数周甚至数月,难以满足工程设计的快速迭代需求。
二、量子算法的 “破局之道”:卡尔曼嵌入 + 格子玻尔兹曼
量子格子玻尔兹曼算法(QLBM)的核心是 “非线性线性化 + 量子并行计算”,通过两大关键步骤破解传统困境:
2.1 格子玻尔兹曼方法(LBM):简化流体建模
LBM 从介观角度描述流体,将流体视为离散速度的粒子群,通过 “碰撞 - 流动” 两步演化逼近纳维 - 斯托克斯方程:
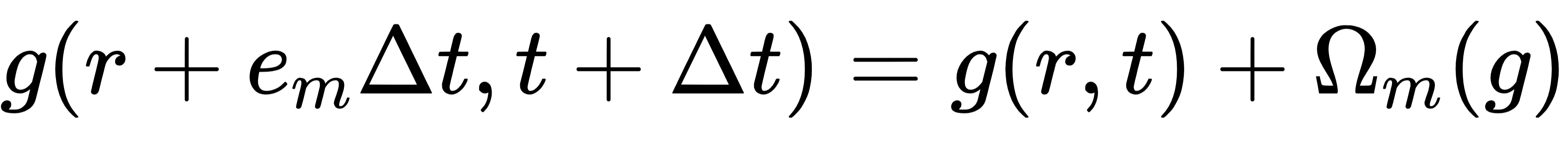
其中g(r,t)是粒子分布函数,em是离散速度,Ωm是碰撞算子(采用 BGK 近似),该形式天然适合并行计算,为量子化奠定基础。
2.2 卡尔曼嵌入:非线性转线性
量子算法仅能处理线性运算,需通过卡尔曼嵌入将非线性项转化为高维线性系统。核心是构造卡尔曼向量:
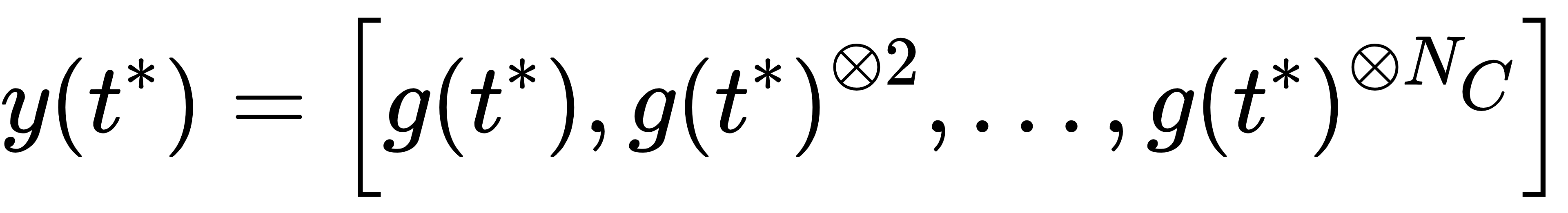
其中NC是卡尔曼截断阶数,向量维度dC=d(dNc−1)/d−1(d=NQ为原始系统维度,N为空间格点数,Q为离散速度数)。嵌入后,非线性演化转化为线性矩阵乘法:
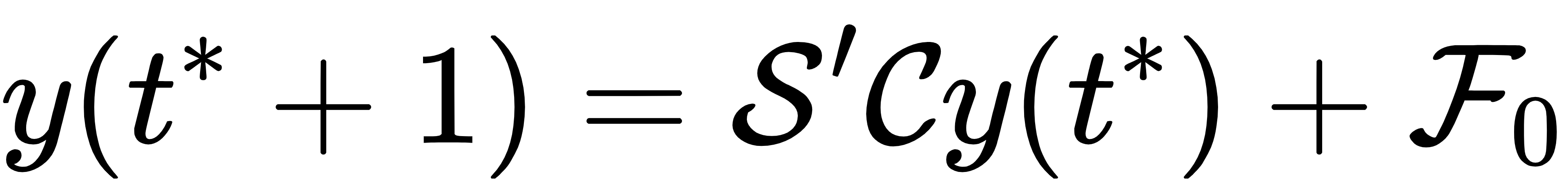
S′和C分别为卡尔曼流动物理矩阵和碰撞矩阵,F0为外力驱动项,该线性系统可通过量子线性求解器(QLS)高效处理。
2.3 边界条件扩展:适配真实场景
团队首次将非周期性边界条件融入量子算法,核心创新包括:
壁面无滑移条件:通过反弹 - back 规则修改流动矩阵,保持矩阵幺正性,可直接通过量子电路实现;
进出口边界:采用非平衡外推方案处理出口自由流,通过部分置换矩阵编码边界节点与内部节点的关联;
外力驱动:通过离散速度空间的力项离散,构造卡尔曼驱动矩阵D,适配移动壁面、体积力等驱动场景。
三、实验验证:三大典型流动的精准预测
团队通过经典数值模拟验证量子算法的有效性,核心结果如下:
3.1 驱动泰勒 - 格林涡
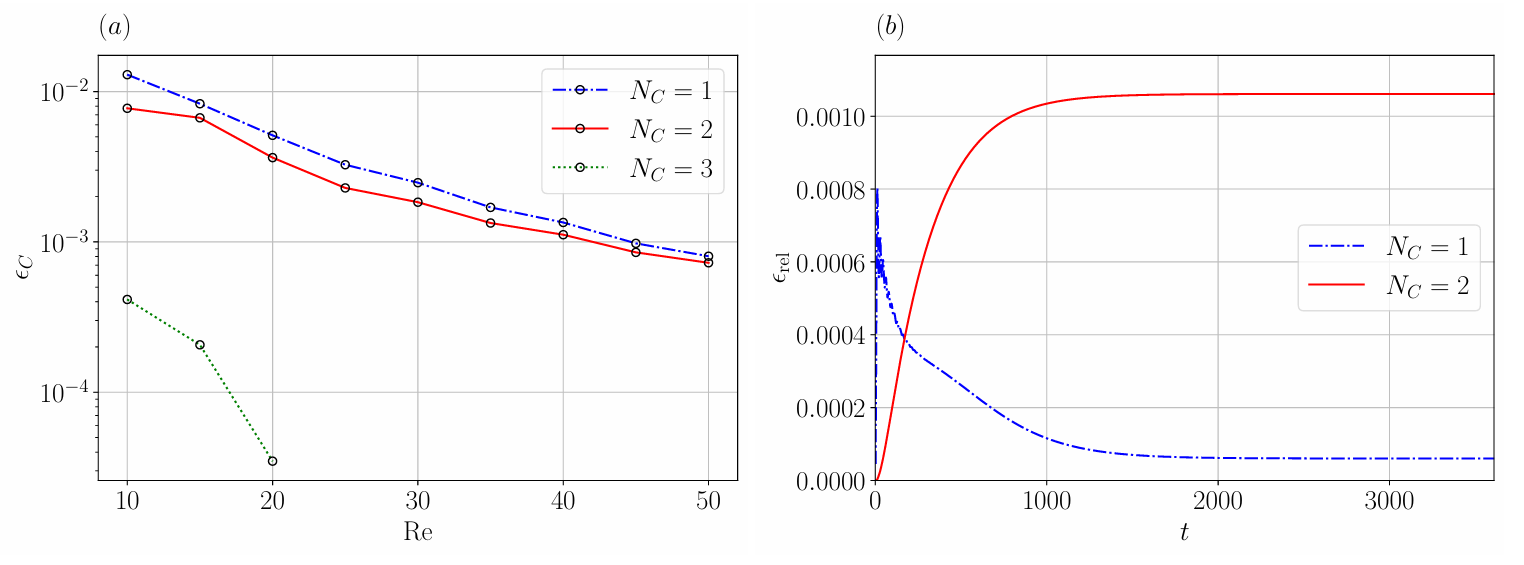
图1 驱动泰勒 - 格林涡的卡尔曼截断误差
当卡尔曼截断阶数NC=3时,相对误差显著降低,在 Re=50、β=0.75条件下,误差随时间演化趋于稳定,不出现发散;
验证了外力驱动下流体从初始零状态向稳态演化的全过程,卡尔曼嵌入能精准捕捉能量守恒与粘性耗散。
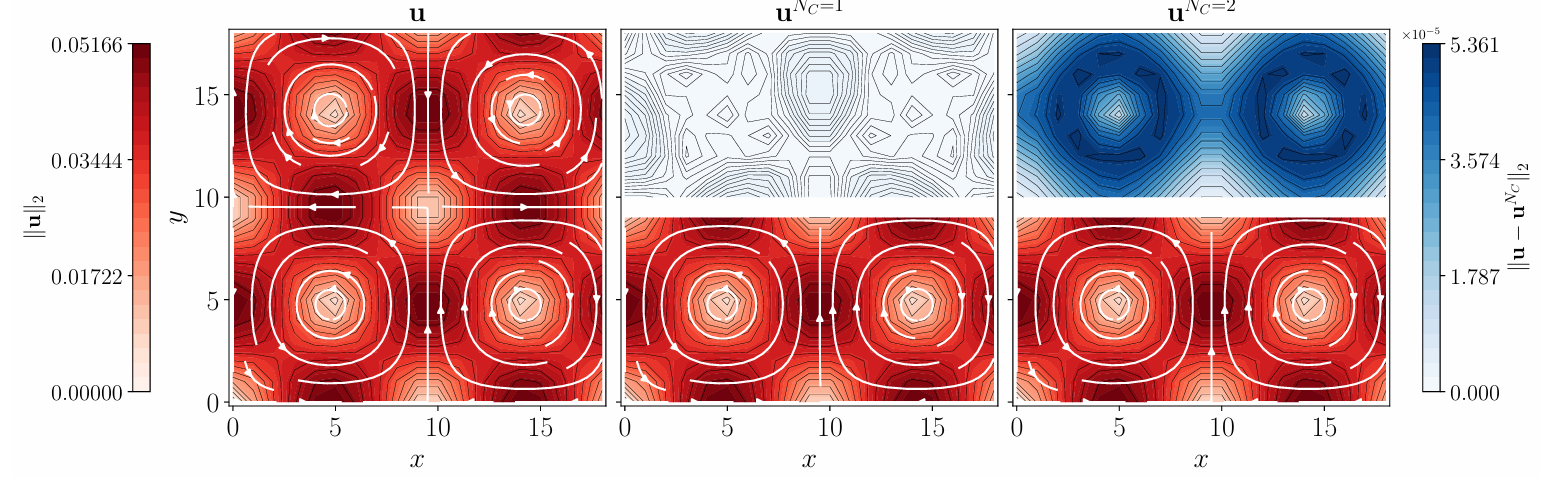
图2 驱动泰勒 - 格林涡的流场空间分布
3.2 顶盖驱动方腔流
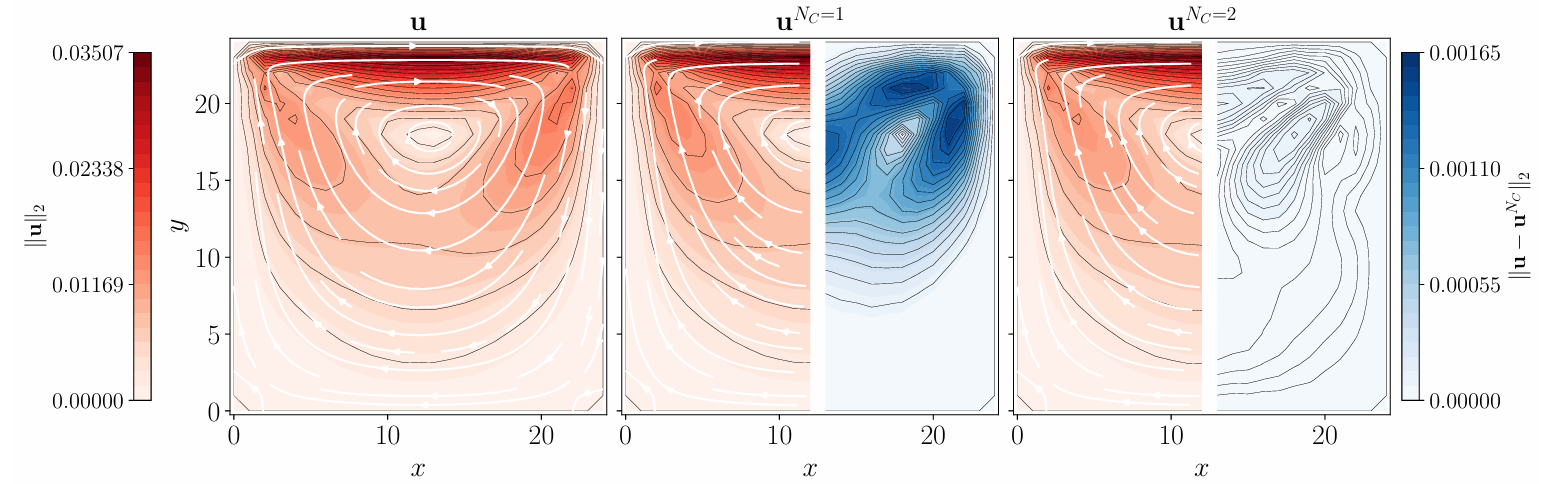
图3 顶盖驱动方腔流的流场与误差
模拟顶盖以恒定速度运动驱动的方腔回流,NC=2较NC=1的截断误差大幅降低,能准确复现腔体内的主回流与角部二次涡;
即使 Re 增至 50,误差仍呈可控增长,证明算法对强剪切流动的适配性。
3.3 圆柱绕流
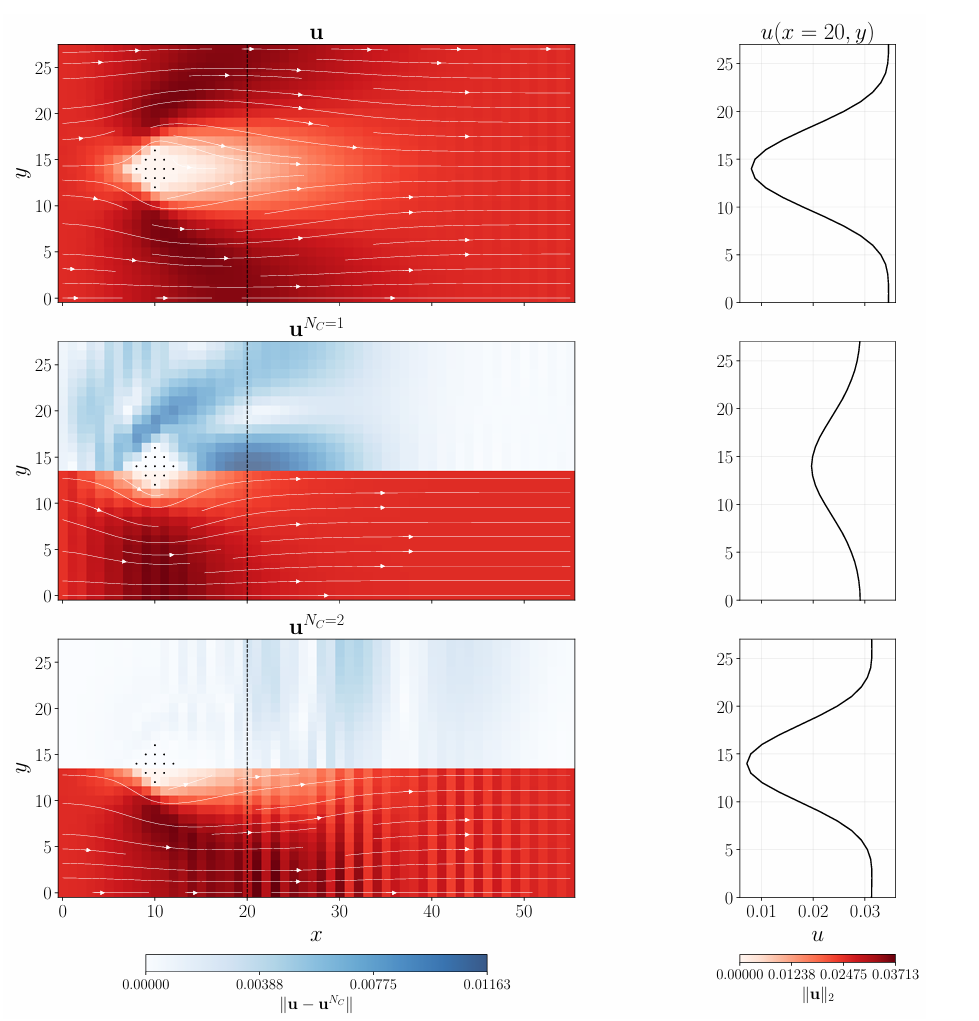
图4 圆柱绕流的流场分布与下游速度剖面
成功模拟低雷诺数(Re≤10)下流体绕圆柱的流动,准确捕捉圆柱后方的速度亏损区与尾流结构;
NC=2时相对误差从NC=1的 7% 降至 2.5%,验证了进出口边界条件处理的有效性。
3.4 量子优势保持
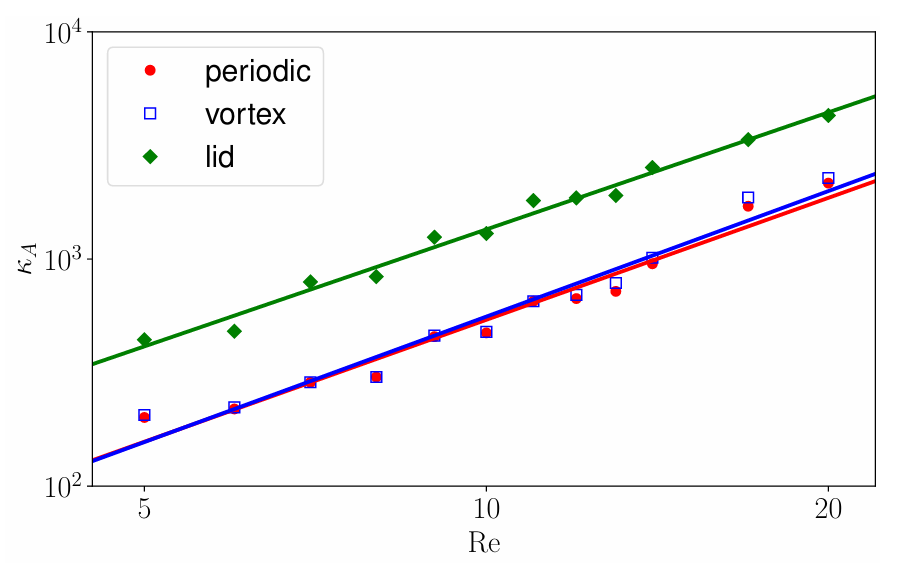
图5 不同流动场景的线性系统条件数
数值分析显示,加入边界条件后,线性系统的条件数κA仍随 Re 弱缩放(O(Re0.375)),远低于经典算法的O(Re2.25),确保量子算法的渐近优势不受影响。量子线性求解器可通过O(αAκAlog1/ϵ)次量子门操作求解,其中αA为块编码系数,展现出指数级算力提升潜力。
四、核心公式:量子线性系统与复杂度
量子算法的最终核心是求解卡尔曼嵌入后的线性方程组:
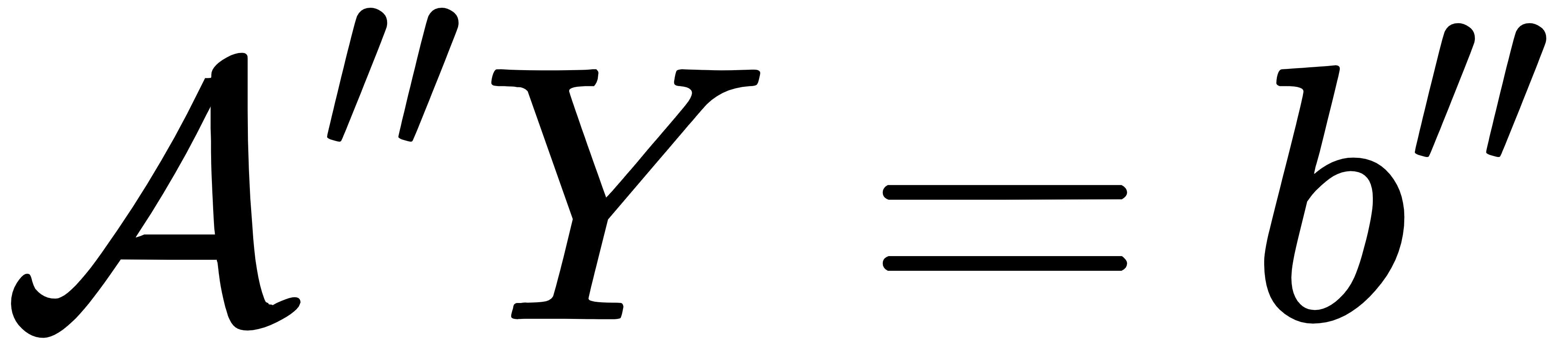
其中A′′是包含流动、碰撞、边界、驱动的高维线性矩阵,Y是卡尔曼历史状态向量。关键复杂度指标为:
量子门复杂度:因边界与驱动引入的额外开销为O(4Nc),随卡尔曼阶数NC多项式增长(NC*通常取 2-3 即可满足精度);
辅助量子比特数:增加5NC+logNC+1个,资源开销可控。
五、应用前景
该算法的突破为量子 CFD 的工程化应用打开广阔空间:
航空航天:快速模拟飞机机翼绕流、发动机内流场,缩短气动设计迭代周期;
海洋工程:精准预测船舶兴波阻力、海洋平台涡激振动,优化结构抗流设计;
能源领域:高效模拟风力机阵列流场、换热器内对流换热,提升能源利用效率。
六、总结
扩展型量子格子玻尔兹曼算法的核心价值,在于首次将量子流体模拟从 “理想周期性流动” 推向 “真实复杂边界流动”,既保持了量子计算对非线性问题的指数级加速潜力,又通过卡尔曼嵌入与边界条件扩展解决了工程适配性难题。尽管目前仍依赖容错量子计算机实现,但该研究已验证量子算法处理真实 CFD 问题的可行性,未来随着量子硬件的成熟,有望将复杂流动模拟时间从数周缩短至小时级,彻底革新工程流体力学的研发范式。
论文链接:[2512.05781] Simulating non-trivial incompressible flows with a quantum lattice Boltzmann algorithm | 











