研究团队与论文信息
论文题目:Advances in physics-informed neural networks for solving complex partial differential equations and their engineering applications
作者:Jiangtao Guoa,b, Hao Zhua,b ,∗, Yujie Yangb, Chenrui Guob
单位:a Key Laboratory of Deep Earth Science and Engineering (Sichuan University), Ministry of Education, Chengdu, 610065, China
b Failure Mechanics and Engineering Disaster Prevention, Key Laboratory of Sichuan Province & Department of Mechanics and Engineering Science, Sichuan University, Chengdu, 610065, China
00 摘要
偏微分方程在工程和科学领域中被广泛用于描述复杂物理系统。然而,传统数值方法在处理高维、强非线性或复杂边界条件问题时,往往面临高昂的计算成本和实现难度。近年来,物理信息神经网络(Physics-Informed Neural Networks, PINNs)作为一种新兴的计算方法,通过将物理定律直接嵌入神经网络训练过程,为求解偏微分方程提供了一种统一而灵活的框架。
本文系统综述了 PINNs 在求解复杂偏微分方程方面的研究进展及其在工程领域中的应用。首先,介绍了 PINNs 的基本原理和数学框架;随后,总结了针对收敛性、稳定性和精度问题所提出的改进策略;进一步讨论了 PINNs 在流体力学、固体力学、电磁学和多物理场问题中的代表性应用;最后,分析了当前方法面临的挑战,并对未来研究方向进行了展望。本文旨在为相关领域研究人员提供系统性的参考和方法总结。
01 研究背景
偏微分方程(Partial Differential Equations, PDEs)是描述自然现象和工程问题的核心数学工具,广泛应用于流体力学、固体力学、电磁学、传热学以及多物理场耦合系统。然而,随着问题维度的提升、几何结构的复杂化以及非线性和多尺度特性的引入,传统数值方法(如有限元法、有限差分法和有限体积法)在计算成本、网格生成和稳定性方面面临明显挑战。
近年来,深度学习方法被逐步引入科学计算领域,其中物理信息神经网络(Physics-Informed Neural Networks, PINNs)通过将控制方程、初始条件和边界条件直接嵌入损失函数,为求解 PDE 提供了一种无需网格的计算框架。该论文系统回顾了 PINNs 在复杂 PDE 求解及工程应用中的最新研究进展,重点分析了方法原理、改进策略、典型应用和未来发展方向。
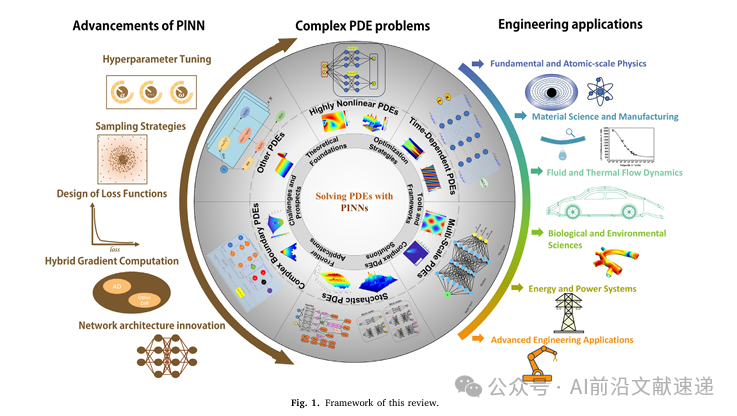
02 PINNs 的基本原理与数学框架
2.1 核心思想
PINNs 的核心思想是使用神经网络近似 PDE 的解函数,并通过自动微分精确计算网络输出关于空间和时间变量的导数。与传统纯数据驱动模型不同,PINNs 将物理控制方程作为约束条件直接引入损失函数,从而减少对大量标注数据的依赖。
在数学形式上,假设 PDE 表达为:
N[u(x,t)]=0
其中N表示微分算子,PINNs 通过构建神经网络 uθ(x,t)来逼近真实解。
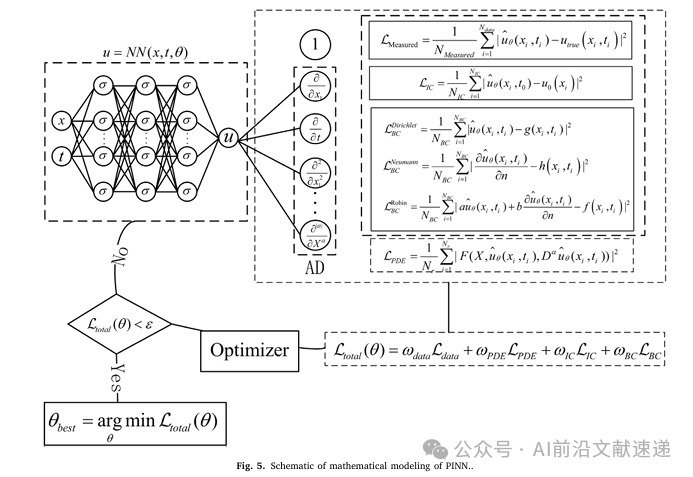
2.2 损失函数构成
论文指出,PINNs 的损失函数通常由以下三部分组成:
1.PDE 残差损失:衡量神经网络预测结果是否满足控制方程;
2.初始条件损失:确保在初始时刻的解满足物理约束;
3.边界条件损失:保证解在边界上的一致性。
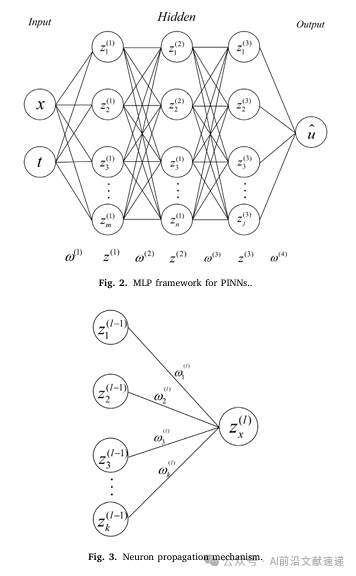
该结构在论文图 2中以示意图形式进行了总结,清晰展示了 PINNs 的训练流程和信息流向(对应原文 Fig. 2)。
03 PINNs 在复杂 PDE 中的关键改进策略
论文系统总结了针对传统 PINNs 在实际应用中暴露的问题所提出的多种改进方法。
3.1 训练稳定性与收敛性改进
原始 PINNs 在面对刚性问题或多尺度 PDE 时,常出现训练不稳定或收敛缓慢的问题。对此,研究者提出了:
· 自适应损失权重策略
· 基于梯度归一化的优化方法
· 多阶段或分域训练策略
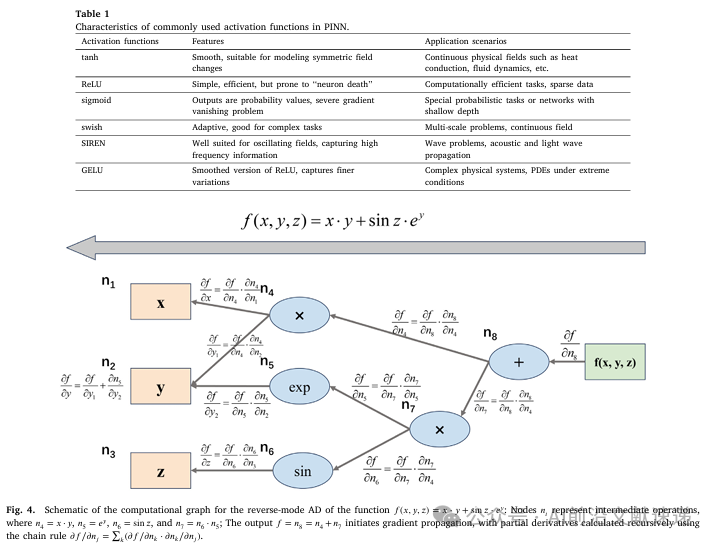
这些方法在论文表 1中进行了归纳对比(对应原文 Table 1)。
3.2 网络结构与表示能力增强
为提升网络对高频解和复杂结构的表达能力,论文总结了以下方向:
· 使用残差网络或深层全连接网络
· 引入傅里叶特征映射(Fourier features)
· 采用多尺度神经网络结构
相关网络结构示意在论文图 5中给出(对应原文 Fig. 5)。
3.3 数据融合与混合方法
论文还指出,PINNs 可与实验数据或高保真数值解相结合,形成“数据—物理混合驱动”的建模框架。这类方法在处理噪声数据或不完全物理模型时具有优势(见原文 Fig. 7)。
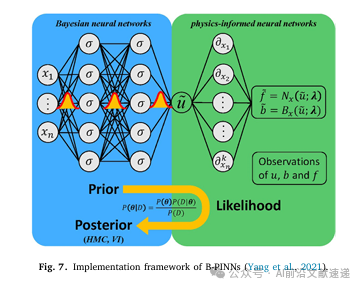
04 工程领域中的典型应用
4.1 流体力学问题
在流体力学中,PINNs 被用于求解 Navier–Stokes 方程,包括层流、湍流以及复杂边界流动问题。论文通过多个案例展示了 PINNs 在无网格条件下重构流场的能力,对应示例结果见图 9。
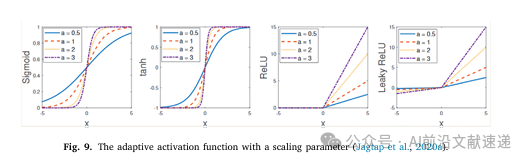
4.2 固体力学与结构分析
针对弹性力学和断裂力学问题,PINNs 能够在不显式构建网格的情况下预测应力和位移场。相关数值结果和误差分析见论文图 11。
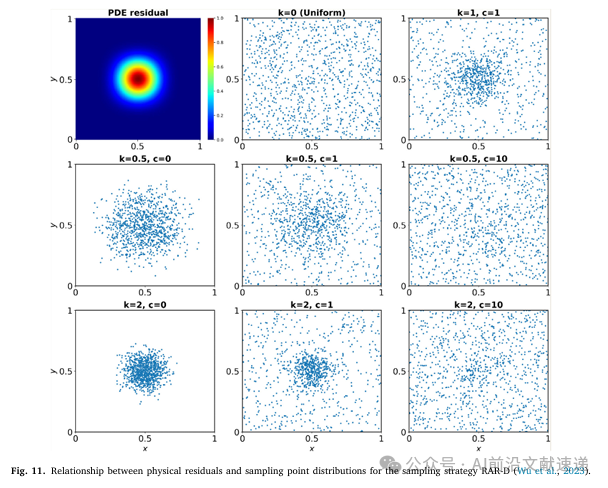
4.3 多物理场耦合问题
论文强调,PINNs 在处理热-结构、电-磁-力耦合等多物理场问题时具有统一建模优势。典型应用示例在图 13中给出。
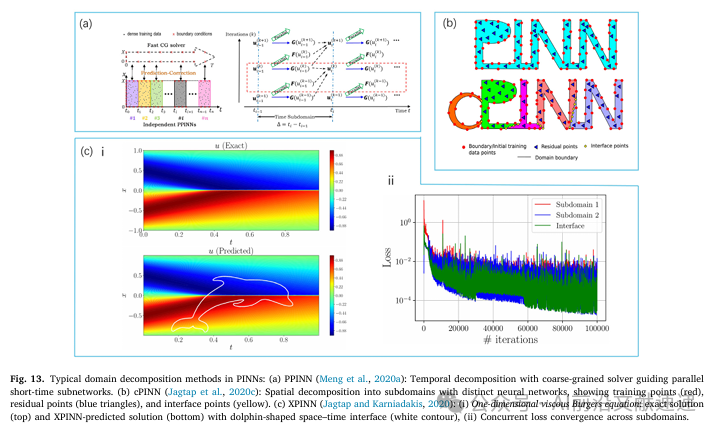
05 当前挑战与发展趋势
尽管 PINNs 在多个领域展现出潜力,但仍存在以下挑战:
· 高维问题中的计算效率问题
· 超参数选择的经验依赖性
· 理论收敛性与误差界限尚不完善
针对这些问题,作者提出未来研究可集中于理论分析、算法加速以及与传统数值方法的深度融合。
06 结论(完整翻译)结论
物理信息神经网络作为一种将物理约束与深度学习相结合的新型计算方法,为求解复杂偏微分方程提供了新的思路。本文系统回顾了 PINNs 的基本原理、关键改进方法及其在工程领域中的典型应用。现有研究表明,PINNs 在高维、非线性和多物理场问题中具有显著优势,但在计算效率、训练稳定性和理论分析方面仍面临挑战。
未来,随着算法改进、计算硬件发展以及理论研究的深入,PINNs 有望在科学计算和工程建模中发挥更加重要的作用。本文的综述可为相关领域研究人员理解和应用 PINNs 提供参考。
论文链接:https://www.sciencedirect.com/science/article/pii/S0952197625020524
本推文仅对原文献进行简要分享,研究团队的相关信息已在开头注明,如有侵权或信息不准确之处,请通过后台联系。
文章改编转载自微信公众号:AI前沿文献速递
原文链接:https://mp.weixin.qq.com/s/z8da-OTuGOCFzg61HrJ07A?scene=1&click_id=2 | 











