3.1 适配参数精度（8bit整数）

在实际问题的求解中，量子硬件平台对参数精度存在较为严格的限制，如相干伊辛机CIM仅支持8位整数范围$[-128,127]$，使得建模时必须精密控制系数动态范围以确保计算可行性。值得注意的是，虽然Ising模型更贴近物理实现，但QUBO模型因其直观的二进制变量表达和约束处理机制，仍是组合优化问题建模的首选形式。这也解释了为何在8位精度限制下，我们仍需要通过QUBO建模后再进行模型转换。

当用户构建QUBO模型时，需特别关注以下两个核心环节：首先，模型转换过程必须保证Ising矩阵的系数严格落在硬件支持的动态范围内；其次，针对不同问题特性，需要灵活选择精度适配策略（如动态范围压缩或变量拆分）。本节提供了四种使用Kaiwu SDK降精度的参考方案。需要强调的是，最优方法往往取决于具体问题的矩阵特性——对于元素差异较小的稀疏矩阵，直接缩放取整可能已足够；而对于存在极端值的密集矩阵，则需采用更精细的变量拆分技术。

通过本节内容学习，在面对8位精度的硬件限制，各位开发者可充分利用QUBO模型的建模优势，最终转化为符合量子计算硬件要求的Ising模型。本节以Kaiwu SDK最新版本v1.3.0版本为例。

1. 背景介绍

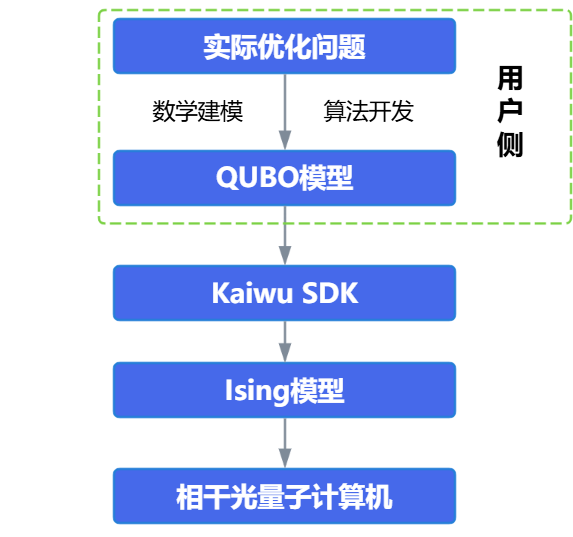
如上图所示，因为QUBO模型只是数学模型，Ising模型是贴近物理实现的模型，所以无论使用的是QUBO还是Ising模型，最终进行CIM真机求解的都是Ising模型。因此，前文提到的8位整数范围的精度限制，是对Ising模型的精度限制，而非对QUBO模型的限制。为了更好地检查如何限制QUBO矩阵，使得建模符合精度限制，下文将讲解QUBO转化为Ising模型的方法，并介绍这样限制的原因。

1.1 为什么要降精度为8bit？

在计算机科学和数字硬件设计中，八位整数（8-bit Integer）是指用8个二进制位（bit）存储的整数。我们所讲的8位整数的取值范围为有符号整数情况下的，最小负数为-128，最大正数为127。

在使用CIM进行计算时，采用8位整数范围（即$[-128,127]$）作为参数精度的标准并非随意选择，而是由量子硬件的物理特性与计算需求共同决定的，也即目前而言，8位精度在计算精度与硬件可实现性之间达到了最佳平衡。随着技术的发展，未来可能通过误差校正等手段突破这一限制，但在当前阶段，理解并适应8位精度的特性才是充分发挥量子优势的关键。

1.2 如何QUBO转Ising？

这里将回顾下QUBO如何转化为Ising模型，以便于理解动态范围检查如何限制QUBO矩阵。

QUBO模型的哈密顿量表示为：

$${\mathcal{H}}_{QUBO}=\sum _i{q}_{ii}{x}_i+\sum _{i\ne j}{q}_{ij}{x}_i{x}_j$$

其中$x_i\in \{0,1\}$为二进制变量，$q_{ii}$和$q_{ij}$分别为线性项和二次项的系数，由于二进制变量满足$x_i^2=x_i$，QUBO模型的对角线元素可直接表示线性项。

Ising模型的变量定义为：自旋变量$si\in \{-1,+1\}$，其哈密顿量为：

$${\mathcal{H}}_{Ising}=\sum _i{h}_i{s}_i+\sum _{i<j}{J}_{ij}{s}_i{s}_j$$

其中$h_i$为局部磁场，$J_{ij}$为自旋间耦合强度。

为了将QUBO模型映射到Ising模型，需进行变量替换。令$s_i=2x_i-1\in \{1,-1\}$，将$x_i$代入QUBO哈密顿量后展开：

$$\begin{array}{rl}{\mathcal{H}}_{Ising}=& \sum _i{q}_{ii}\cdot \frac{s_i+1}{2}+\sum _{i\ne j}{q}_{ij}\cdot \frac{(s_i+1)(s_j+1)}{4}\\ =& \sum _{i\ne j}\frac{q_{ij}}{4}{s}_i{s}_j+\sum _i(\frac{q_{ii}}{2}+\frac{\sum _{k\ne i}(q_{ik}+q_{ki})}{4})s_i+(\frac{\sum _i{q}_{ii}}{2}+\frac{\sum _{i\ne j}{q}_{ij}}{4})\end{array}$$

由此可得Ising模型的系数：

$$\begin{array}{rl}{J}_{ij}& =\frac{q_{ij}}{4}\\ h_i& =\frac{q_{ii}}{2}+\frac{1}{4}\sum _{k\ne i}(q_{ik}+q_{ki})\end{array}$$

其中$h_i$为线性项，因为CIM真机无法直接解决包含线性项的伊辛问题，需要增加一个辅助变量转化为二次项，故将QUBO矩阵转化为Ising矩阵时，Ising矩阵通常会多一个比特（即变量），辅助变量取1和-1时可以分别对应到添加辅助变量前的两组解，故添加辅助变量后与原问题等价，此为正常现象，用户无需过多担心。

1.3 常见问题说明

（1）Ising矩阵强调的8位整数范围和矩阵内的具体数字没有直接关系，若矩阵元素整体缩放同比例后仍处于8位整数范围内，同样符合计算要求。例：（1280，1000）等价于（128，100）；

（2）为什么Ising矩阵的线性项不能放在对角线元素上？

QUBO变量满足$x^2=x$，可以用矩阵的对角线元素表达线性项，而Ising模型$x^2=1$，不能这样表示。常数项在优化过程中通常可忽略，但在计算总能量时需额外累加，常数项单独记录，在计算最终哈密顿量时加上即可。

以一个简单的QUBO模型为例：

$$\begin{array}{r}{x}^{\mathrm{\top }}\left(\begin{array}{ll}0& 2\\ 1& 1\end{array}\right)x\end{array}$$

经过变换之后的Ising模型为：

$$\begin{array}{r}{s}^{\mathrm{\top }}\left(\begin{array}{lll}0& 3/8& 3/8\\ 3/8& 0& 5/8\\ 3/8& 5/8& 0\end{array}\right)s+3/2\end{array}$$

（3）QUBO矩阵转Ising矩阵时增加一个比特（变量）的说明

引入一个辅助自旋变量$s_a$，并将问题重新表述为：

$$mi{n}_{s_a,s_1,s_2,...s_N}-\sum _{i=1}^N{h}_i{s}_i{s}_a-\sum _{i\ne j}{J}_{ij}{s}_i{s}_j$$

这种重新表述消除了线性项，使其适合于不支持偏置项的CIM真机，但这导致的辅助伊辛问题有两个简并解：$[\{\widehat{s_i}{\}}_{i=1}^N,{\hat{s}}_a=1]$和$[\{-\widehat{s_i}{\}}_{i=1}^N,{\hat{s}}_a=-1]$，其中$\{\widehat{s_i}{\}}_{i=1}^N$表示原始伊辛问题的解，因此可以从辅助问题的解中获得原始问题的解。

证明

要解决的伊辛问题是：

$$J(\hat{\mathbf{s}})=\underset{\mathbf{s}\in \{-1,1{\}}^N}{min}-{\mathbf{h}}^T\mathbf{s}-{\mathbf{s}}^T\mathbf{J}\mathbf{s}$$

其中$\hat{\mathbf{s}}$是最优解，辅助伊辛问题定义为：

$$J_a(\overline{\mathbf{s}},{\hat{s}}_a)=\underset{\mathbf{s}\in \{-1,1{\}}^N\text{,}{s}_a\in \{-1,1\}}{min}-({\mathbf{h}}^T\mathbf{s})s_a-{\mathbf{s}}^T\mathbf{J}\mathbf{s}$$

其中$(\overline{\mathbf{s}},{\hat{s}}_a)$表示辅助伊辛问题的最优解，$\overline{\mathbf{s}}$和$\hat{\mathbf{s}}$都是$N\times 1$自旋向量。如果$\widehat{s_a}=1$，则$J_a(\overline{\mathbf{s}},1)=J(\hat{\mathbf{s}})$。

下面将证明$\widehat{s_a}=-1$时，$J_a(\overline{\mathbf{s}},-1)=J(\hat{\mathbf{s}})$。

假设相反的情况：

• 如果$J_a(\overline{\mathbf{s}},-1)<J(\hat{\mathbf{s}})$，则$J(-\overline{\mathbf{s}})<J(\hat{\mathbf{s}})$，这与$\hat{\mathbf{s}}$的最优性相矛盾；

• 如果$J_a(\overline{\mathbf{s}},-1)>J(\hat{\mathbf{s}})$，则$J_a(\overline{\mathbf{s}},-1)>J_a(-\hat{\mathbf{s}},-1)$，这与$(\overline{\mathbf{s}},-1)$在辅助问题中的最优性相矛盾。

因此，$J_a(\overline{\mathbf{s}},{\hat{s}}_a)=J(\hat{\mathbf{s}})$。

注意，辅助伊辛问题有两个简并解$(\overline{\mathbf{s}},1)$和$(-\overline{\mathbf{s}},-1)$，其中$\overline{\mathbf{s}}$也是原始伊辛问题的最优解，因此可以从辅助问题的解通过$\hat{\mathbf{s}}=\overline{\mathbf{s}}\cdot \widehat{s_a}$得到原始问题的解。

2. Kaiwu SDK降低精度的方法

Kaiwu SDK提供了四种降低参数精度的方法，分别是直接截断（adjust_ising_matrix_precision）、 动态范围压缩（perform_precision_adaption_mutate）、变量拆分（perform_precision_adaption_split）以及整合了适应性截断和变量拆分的降低精度装饰类（PrecisionReducer）：

• 直接截断方法最简单方便，但是若存在极端值会导致严重的精度损失；
• 动态范围压缩方法在修改矩阵的同时能够保持矩阵的解不变，但能够改变精度的程度取决于矩阵本身的可下降空间；
• 变量拆分方法能够将矩阵修改到任意精度，但是新矩阵的比特数随着精度变化量增长较快。

2.1 方法一：直接截断（adjust_ising_matrix_precision）

直接取整法是最简单的精度调整方案，其实现原理是将矩阵元素全部线性缩放到目标位宽（如8位整型范围-128~127），再执行四舍五入取整。该方法可以通过kaiwu.ising.adjust_ising_matrix_precision或kaiwu.qubo.adjust_qubo_matrix_precision函数实现。

如下表所示，kaiwu.ising.adjust_ising_matrix_precision是用于调整Ising矩阵精度的直接取整法函数，而kaiwu.qubo.adjust_qubo_matrix_precision能够将QUBO矩阵转换为Ising矩阵，在用直接取整法调整完生成的Ising矩阵的精度后，再将矩阵变为QUBO矩阵的形式输出。

函数	kaiwu.ising.adjust_ising_matrix_precision	kaiwu.qubo.adjust_qubo_matrix_precision
输入	Ising矩阵	QUBO矩阵
方法	直接取整法	直接取整法
流程	Ising矩阵>>>调节后的Ising矩阵	QUBO矩阵>>>对应的Ising矩阵>>>调节后的Ising矩阵>>>调节后对应的QUBO矩阵
输出	调节后的Ising矩阵	调节后的QUBO矩阵

示例代码如下：

import numpy as np
import kaiwu as kw
# 原始矩阵包含微小差异项
ori_ising_mat1 = np.array([[0, 0.22, 0.198],
                           [0.22, 0, 0.197],
                           [0.198, 0.197, 0]])
ising_mat1 = kw.preprocess.adjust_ising_matrix_precision(ori_ising_mat1)
print("调整后矩阵:\n", ising_mat1)

调整前后矩阵的对比如下：

$$\left[\begin{array}{ccc}0& 0.22& 0.198\\ 0.22& 0& 0.197\\ 0.198& 0.197& 0\end{array}\right]\to \left[\begin{array}{ccc}0& 127& 114\\ 127& 0& 114\\ 114& 114& 0\end{array}\right]$$

必须注意，该方法对元素间差异较小的矩阵效果较好，但当矩阵存在极端值时，直接取整会导致严重精度损失。例如对于存在极端值的矩阵：

# 包含极端值的矩阵
ori_ising_mat2 = np.array([[0, 0.22, 0.198],
                           [0.22, 0, 50],
                           [0.198, 50, 0]])
ising_mat2 = kw.preprocess.adjust_ising_matrix_precision(ori_ising_mat2)
print("极端值调整后矩阵:\n", ising_mat2)

输出结果为：

$$\left[\begin{array}{ccc}0& 0.22& 0.198\\ 0.22& 0& 50\\ 0.198& 50& 0\end{array}\right]\to \left[\begin{array}{ccc}0& 1& 1\\ 1& 0& 127\\ 1& 127& 0\end{array}\right]$$

此时，微小项0.22和0.198都被压缩为1，而极端值50被放大到127，但是两者的相对比值由于精度上限(127)以及整数的限制(1)而被扭曲，导致求解结果偏离真实最优解。因此，直接取整法仅推荐在动态范围较小的场景下使用。对于复杂问题，应优先选择下面将要讲到的动态范围压缩或变量拆分方案。

2.2 方法二：动态范围压缩（perform_precision_adaption_mutate）

动态范围（Dynamic Range, DR） 是衡量矩阵系数分布的关键指标，适用于QUBO矩阵和Ising矩阵，通过减小动态范围，可以降低原矩阵所需要的参数精度。

动态范围定义为：

$$DR(X):=lo{g}_2\left(\frac{\hat{D}(X)}{\check{D}(X)}\right)$$

其中，$X$为系数矩阵，$\hat{D}(X)=\underset{i,j}{max}|X_{ij}|$为$X$元素的最大距离，$\check{D}(X)=\underset{i,j}{min}|X_{ij}|$ 为$X$元素的最小距离。

通过矩阵元素重缩放与四舍五入操作，将原始矩阵$Q$映射到硬件支持的8位整数范围（-128~127），同时保持最优解不变。

具体步骤为：首先，设缩放因子为$\alpha$，构造变换$Q^{\prime }=\lfloor \alpha Q\rceil$，其中$\lfloor \cdot \rceil$表示四舍五入取整。

缩放因子需满足：

$$\alpha \le \frac{127}{\hat{D}(Q)}$$

此时变换后的矩阵满足$Q_{ij}^{\prime }\in [-128,127]$。

理论证明，当$\alpha$满足：

$$\alpha >\frac{\mathrm{\Delta }}{2\check{D}(Q)}$$

（其中$\mathrm{\Delta }$为相邻可区分参数的最小间隔），可保证$Q\subseteq Q^{\prime }$，即原问题最优解包含于新问题解集中。

动态范围的定义可以适用于QUBO矩阵和Ising矩阵，通过减少动态范围，可以降低原矩阵所需要的参数精度。由于最终在Ising矩阵上进行计算，所以Kaiwu SDK降低动态范围的操作直接作用于Ising矩阵。

Kaiwu SDK主要使用函数perform_precision_adaption_mutate进行动态范围压缩。以下矩阵为例：

$$Q_0=\left[\begin{array}{ccccc}0& -20& 0& 40& 1.1\\ 0& 0& 12240& 1& 120\\ 0& 0& 0& 0& -10240\\ 0& 0& 0& 0& 2.05\\ 0& 0& 0& 0& 0\end{array}\right]$$

经过perform_precision_adaption_mutate处理后，动态范围从$DR(Q_0)=13.2$降至$DR(Q^{\prime })=7.1$，同时保持最优解不变。

详细代码如下：

import kaiwu as kw
import numpy as np
# 原始QUBO矩阵
mat0 = np.array([[0, -20, 0, 40, 1.1],
                [0, 0, 12240, 1, 120],
                [0, 0, 0, 0, -10240],
                [0, 0, 0, 0, 2.05],
                [0, 0, 0, 0, 0]])
# 执行mutate方法降低精度
mutated_mat = kw.preprocess.perform_precision_adaption_mutate(mat0)
print("调整后矩阵:\n", mutated_mat)

运行该程序，得到调整后的矩阵为：

$$Q^{\prime }=\left[\begin{array}{ccccc}0& -2.05& 0& 40& 0\\ 0& 0& 4.1& 0& 0\\ 0& 0& 0& 0& -2.05\\ 0& 0& 0& 0& 2.05\\ 0& 0& 0& 0& 0\end{array}\right]$$

2.3 方法三：变量拆分（perform_precision_adaption_split）

由于当前量子计算机对Ising系数的存储方式为定点数，且只有8位精度，对于最大最小值的比值超过$2^8$的多项式，需要将系数大的项分拆。实现方式为将原式中的比特替换成值相等的多个等价比特，相等条件由约束项实现，从而使得每一项的系数都能够缩小。当矩阵参数动态范围超过硬件支持的$2^8$时，需采用变量拆分技术。

设目标函数为：

$$f(\mathbf{x})=\sum _i{q}_i{x}_i+\sum _{i<j}{q}_{ij}{x}_i{x}_j$$

对于满足$|q_{ij}|>2^{16}$的项，引入辅助变量${\mathbf{x}}^{\prime }$将其分解，构造等价问题：

$$\begin{array}{rl}\underset{\mathbf{x},{\mathbf{x}}^{\prime }}{min}& f(\mathbf{x},{\mathbf{x}}^{\prime })+M\sum _k(x_k-x_k^{\prime }{)}^2\\ \text{其中}& f(\mathbf{x},{\mathbf{x}}^{\prime })=\sum _i{q}_i{x}_i+\sum _{i<j}\lfloor \frac{q_{ij}}{2}\rfloor x_i{x}_j+\sum _{i<j}\lceil \frac{q_{ij}}{2}\rceil x_i^{\prime }{x}_j^{\prime }\end{array}$$

拆分的方式将$f(\mathbf{x})$转化为：

$$\begin{array}{rl}& f(\mathbf{x},{\mathbf{x}}^{\prime })+M\sum _i(x_i-x_{i1}{)}^2+M\sum _{i,j}(x_{ij}-x_{i(j+1)})=\\ & f(\mathbf{x},{\mathbf{x}}^{\prime })+M\sum _i(x_i+x_{i1}-2x_i{x}_{i1})+M\sum _{i,j}(x_{ij}+x_{i(j+1)}-2x_{ij}{x}_{i(j+1)})\end{array}$$

例如，对于$x_1+2x_2+200x_3$，要求多项式系数最大最小值的比值不能超过150，那么将多项式修改为：

$$x_1+2x_2+100x_3+100x_{31}+50(x_3-x_{31}{)}^2=x_1+2x_2+100x_3+100x_{31}+50(x_3+x_{31}-2x_3{x}_{31})$$

import kaiwu as kw
import numpy as np
mat = np.array([[0, -15,0, 40],
                [-15,0, 0, 1],
                [0,  0, 0, 0],
                [40, 1, 0, 0]])
splitted_ret, last_idx = kw.preprocess.perform_precision_adaption_split(mat, 4)
print(splitted_ret)

min_increment计算得到默认值为1，精度设置为4个比特，范围在$[-7,7]$，也即绝对值应该小于7。程序输出转换后的矩阵如下：

如图所示，红色的箭头指示出拆分前后的对应关系，蓝色框中的数字则是用于限制新建的变量的值保持一致的惩罚项，通过这样拆分变量，可以在保持原矩阵的解的情况下，将参数精度降低。降低精度的过程通过param_bit，min_increment，penalty，round_to_increment等参数来调节。

其中，min_increment（最小步长）参数用于降低元素精度，同时保持原始数据的相对差异。该参数使矩阵的值满足min_increment的整数倍（如min_increment=0.5时，元素只能为 0, 0.5, 1.0 等），其默认值为自动计算矩阵元素间的最小正差值（如矩阵中有 0.1 和 0.3，则默认min_increment=0.2）。

round_to_increment（舍入策略）参数为了使得调整元素时，确保所有元素之和严格等于原值。例如，不启用reduce_error时，15将被拆分成7.5+7.5，若分别近似取整会变成8+8，总和发生偏离（15 → 16）。启用reduce_error=True后，通过动态调整部分元素的舍入方向（ 7.5 → 7 或 8），使总和严格等于原值（如 15 → 7+8=15）。

演示代码如下：

splitted_ret2, last_idx2 = kw.preprocess.perform_precision_adaption_split(mat, 4, min_increment=3, round_to_increment=True)
print(splitted_ret2)

结果为：

$$\left[\begin{array}{cccccc}0& 21.& -6.& 0.& 3.& 12.\\ 21& 0.& -9.& 0.& 12.& 12.\\ -6& -9.& 0.& 0.& 0.& 0.\\ 0& 0.& 0.& 0.& 0.& 0.\\ 3& 12.& 0.& 0.& 0.& 21.\\ 12& 12.& 0.& 0.& 21.& 0.\end{array}\right]$$

对拆分后精度满足要求的矩阵进行求解后，可以通过restore_splitted_solution函数将其恢复成原矩阵的解。

worker = kw.cim.SimulatedCIMOptimizer(iterations=1000)
output = worker.solve(splitted_ret)
sol = output[0]
org_sol = kw.preprocess.restore_splitted_solution(sol, last_idx)
print(org_sol)

结果为：

$$\left[\begin{array}{cccc}-1.& 1.& -1.& -1.\end{array}\right]$$

2.4 方法四：降低精度装饰类（PrecisionReducer）

降低精度装饰类（PrecisionReducer）是Kaiwu SDK中一种智能化的精度适配方案，其核心思想是：通过截断与变量拆分的组合策略，将原始矩阵参数适配到硬件支持的精度范围内。该方案以装饰器模式实现，用户可将任意优化器作为基础组件传入，PrecisionReducer会在求解过程中自动完成矩阵精度调整，同时保证解的可行性。即当用户在提交量子计算机求解时，可以在CIMOptimizer之外再套一个PrecisionReducer，然后把PrecisionReducer作为Optimizer传给Solver。

装饰类的工作原理分为两个阶段：截断与变量拆分决策。当用户设定目标精度（precision参数）后，装饰类首先计算矩阵的动态范围，若动态范围超过硬件限制（由target_bits参数控制），则优先尝试通过一定程度上的适应性截断降低动态范围；若截断后仍无法满足精度要求，则自动触发变量拆分操作，将大系数项分解为多个等效变量，并通过惩罚项约束其等价性。详细示例代码如下：

import kaiwu as kw
# 启用详细日志输出
kw.utils.set_log_level("INFO")
# 定义原始Ising矩阵
matrix = -np.array([[ 0. ,  1.23 ,  0. ,  1. ,  1. ],
                    [ 1.23 ,  0. ,  0. ,  1.,   1. ],
                    [ 0. ,  0. ,  0. ,  1.,   1. ],
                    [ 1. ,  1.,   1. ,  0. ,  1. ],
                    [ 1. ,  1.,   1. ,  1. ,  0. ]])
# 创建基础优化器（模拟退火）
base_optimizer = kw.classical.SimulatedAnnealingOptimizer(
    initial_temperature=100,
    alpha=0.99,
    cutoff_temperature=0.001,
    iterations_per_t=10,
    size_limit=5
)
# 添加精度降级装饰器（目标精度8位）
precision_optimizer = kw.cim.PrecisionReducer(base_optimizer, precision=8)

# 执行求解
solution = precision_optimizer.solve(matrix)

装饰类的核心参数only_feasible_solution控制解的可行性验证。当设为True时，装饰类会过滤所有违反拆分约束的解（通过惩罚项判断），若所有解均不可行则抛出异常；当设为False时，允许返回非可行解（可能存在拆分变量不一致的情况）。

更多使用细节，可直接参考kaiwu.preprocess package文档：https://kaiwu-sdk-docs.qboson.com/zh/v1.2.0/source/modules/kaiwu.preprocess.html