4.2 调整惩罚系数
案例:基于松弛变量的JSP问题QUBO建模
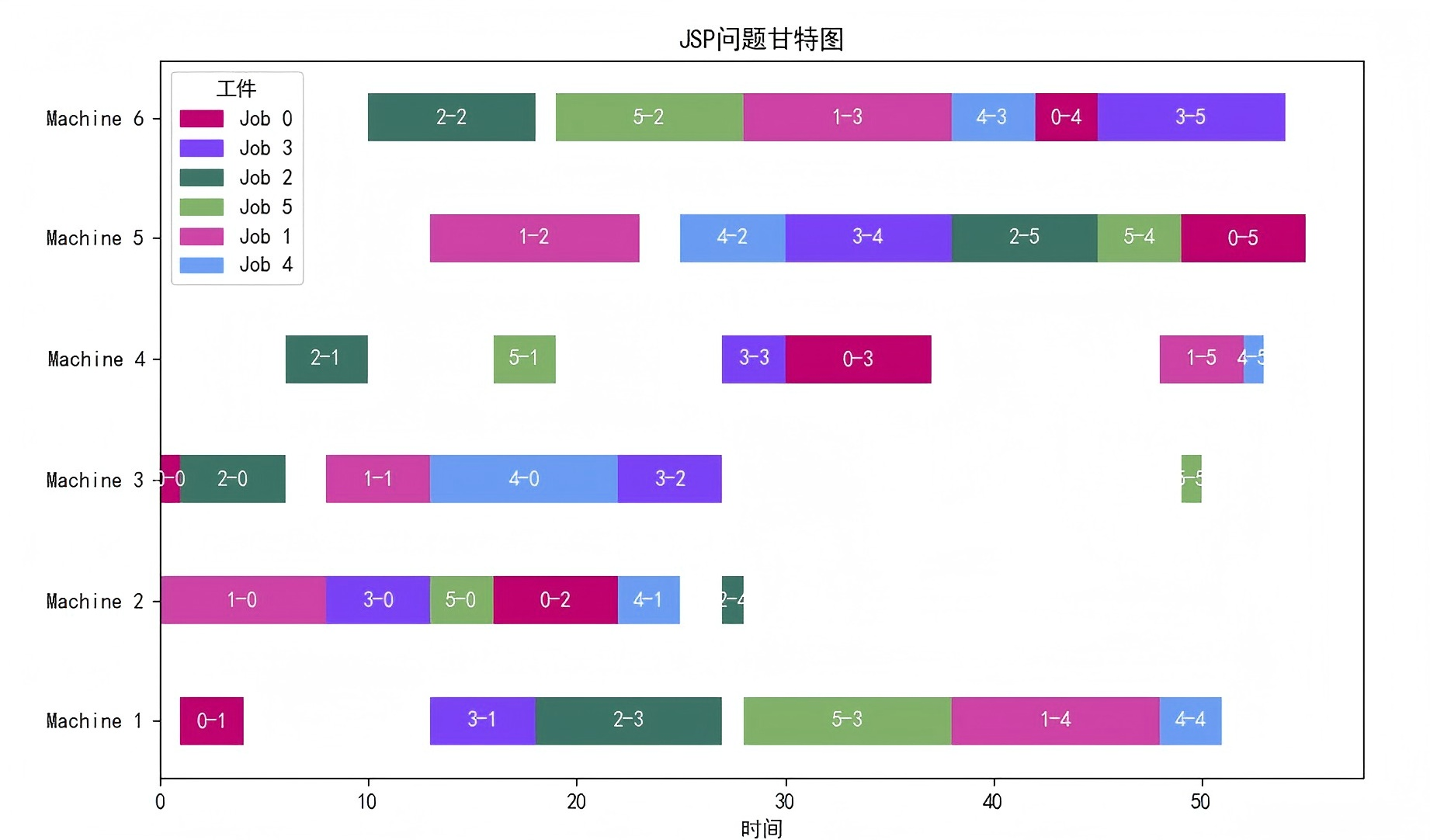
JSP问题是一个复杂的组合优化问题,目标是在满足一定的约束条件下,合理地分配资源,优化生产过程中的作业顺序,以最小化完成所有任务的总时间、最大化资源利用率或降低成本等,基于CIM和Kaiwu SDK可以轻松求解。
在任务调度模型中,假设与约束条件总结如下:
(1)各任务仅包含一道工序;
(2)各任务的加工时间已知,与机器无关;
(3)一台机器在任意时刻最多只能处理一个任务;
(4)每个任务可以分配到任意一台机器加工,且只能在一台机器上加工;
(5)每个机器可以有不同的空闲开始时间。
 JSP示意图
JSP示意图 和任务调度模型一样,这个问题的QUBO建模常常包含多种约束,每种约束针对不同实体会产生多个约束条件。使用QUBO建模需要将约束条件转为约束项并给定合适的惩罚系数,如果惩罚系数过大,会导致系数矩阵的精度超过相干光量子计算机的精度限制,如果惩罚系数过小,会导致求解的过程中的约束条件无法优先满足,最优解不是可行解的情况。因此,对于这种存在大量约束条件的问题,需要一些方法自动为每个约束确定惩罚系数。
定义变量
约束(1)表示最晚完成时间
将上面的模型转为QUBO形式,由于
其中
下一步将不等式约束(1)通过增加松弛变量
由于松弛变量也是整数,将其二进制化,约束(1)可进一步表示为:
为了将等式约束化为目标函数的一部分从而满足QUBO形式,将等式约束改写为
其中,我们需要处理两类核心约束:
(1)任务分配约束(硬约束)
该约束确保每个任务必须分配到唯一机器,使用下界法计算惩罚系数下界:
(2)机器时间约束(松弛等式)
该约束通过松弛变量转化,需计算二次惩罚项系数:
总结
本文介绍了自动确定惩罚系数的方法,包括惩罚法(Penalty Method)、下界法直接估计和迭代确定三种思路。这些方法可有效解决在量子计算中惩罚系数难以确定的问题,为求解大规模组合优化问题提供新的思路。通过不断优化惩罚系数,可以在满足约束条件的同时,更好地优化目标函数,从而提高求解效率和质量。
显然,基于Kaiwu SDK,用户只需关注建立与场景所对应的数学模型,SDK提供的方法可以自动确定惩罚系数,这将极大降低使用相干光量子计算机求解实际问题的难度。
