4.1 处理约束问题

案例：最小顶点覆盖问题（MVCP）

为了更好地巩固前面所学的处理约束方法，本节将以图论中一个经典优化问题——最小顶点覆盖问题（MVCP） 为例，对其约束过程进行详细讲解。MVCP在电力、社交网络等领域应用非常广泛，如电力数据网的探针部署问题就可以抽象为无向图的最小顶点覆盖问题。

给定一个无向图，其顶点集为$V$，边集为$E$，顶点覆盖是指顶点的一个子集，使得图中的每条边至少有一个端点属于该子集。最小顶点覆盖问题的目标是找到包含最少顶点的覆盖子集。设二元变量$x_j=1$表示顶点$j$被选入覆盖子集，否则$x_j=0$。则该问题的标准带约束0-1线性规划模型为：

$$\begin{array}{rl}min& \sum _{j\in V}{x}_j\\ s.t.& x_i+x_j\ge 1\mathrm{\forall }(i,j)\in E\\ & x_j\in \{0,1\}\end{array}$$

其表示最优化目标是最小化覆盖子集的顶点数量，约束条件确保每条边的至少一个端点被选入覆盖子集。值得注意，每条边对应一个逻辑或约束条件，因此即使对于中等规模的图，约束数量也可能非常庞大。

在QUBO模型中，每个约束将通过向目标函数添加惩罚项的方式隐式处理。根据前文表格中列出的方法，约束条件$x_i+x_j\ge 1$可转化为惩罚项：$P\cdot (1-x_i-x_j+x_i{x}_j)$。因此，原带约束模型可等价转化为无约束QUBO模型：

$$\text{min}\sum _{j\in V}{x}_j+P\sum _{(i,j)\in E}(1-x_i-x_j+x_i{x}_j)$$

忽略常数项后，可将其重写为标准QUBO形式：

$$\text{min}{\mathbf{x}}^{T}Q\mathbf{x}$$

其中$Q$矩阵通过合并线性项和二次项系数构建。若每个顶点$j$具有权重$w_j$，则加权最小顶点覆盖问题的QUBO模型为：

$$\text{min}\sum _{j\in V}{w}_j{x}_j+P\sum _{(i,j)\in E}(1-x_i-x_j+x_i{x}_j)$$

接下来我们考虑一个实际例子，对于下面这个有n=6条边和m=5个节点的图，我们想确定最小的顶点覆盖度。

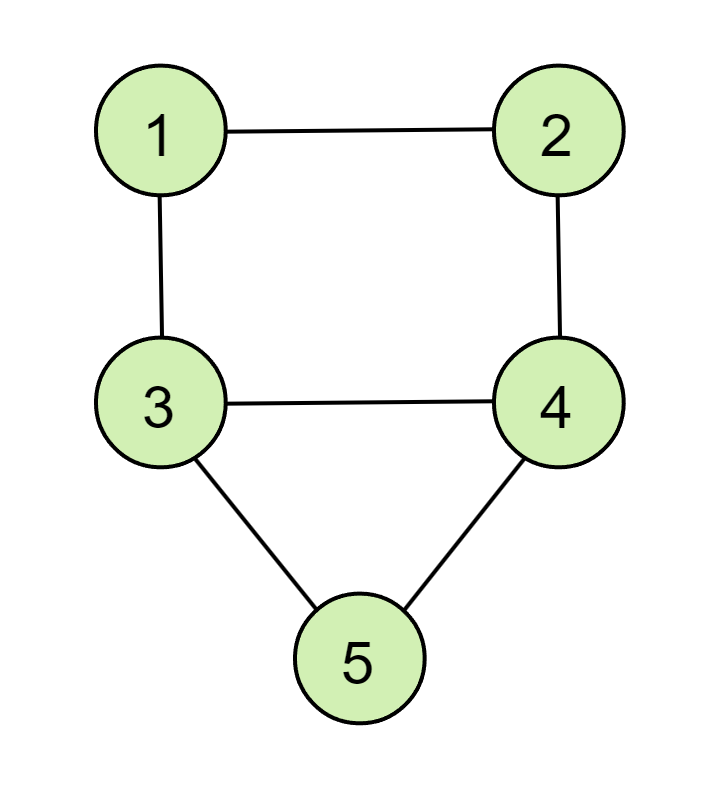
此时，优化问题可以写成：

$$\begin{array}{rl}\text{Minimize }y& =x_1+x_2+x_3+x_4+x_5\\ & +P(1-x_1-x_2+x_1{x}_2)\\ & +P(1-x_1-x_3+x_1{x}_3)\\ & +P(1-x_2-x_4+x_2{x}_4)\\ & +P(1-x_3-x_4+x_3{x}_4)\\ & +P(1-x_3-x_5+x_3{x}_5)\\ & +P(1-x_4-x_5+x_4{x}_5)\end{array}$$

简化后可以得到：

$$\begin{array}{rl}y& =(1-2P)x_1+(1-2P)x_2+(1-3P)x_3\\ & +(1-3P)x_4+(1-2P)x_5\\ & +P(x_{12}+x_{13}+x_{24}+x_{34}+x_{35}+x_{45})+6P\end{array}$$

任意选择P等于8，去掉加性常数（6P = 48）得到我们的QUBO模型

$$min{x}^{T}Qx$$

其中对称矩阵$Q$为：

$$Q=\left[\begin{array}{ccccc}-15& 4& 4& 0& 0\\ 4& -15& 0& 4& 0\\ 4& 0& -23& 4& 4\\ 0& 4& 4& -23& 4\\ 0& 0& 4& 4& -15\end{array}\right]$$

至此，我们从一个包含5个变量和6个约束的受限模型转换为一个具有相同5个变量的无约束QUBO模型。

求解该 QUBO 模型得到：$x^{T}Qx=-45,x=(0,1,1,0,1)$，对应的目标函数值为：$y=48-45=3$。最小顶点覆盖由节点2、3和5组成。

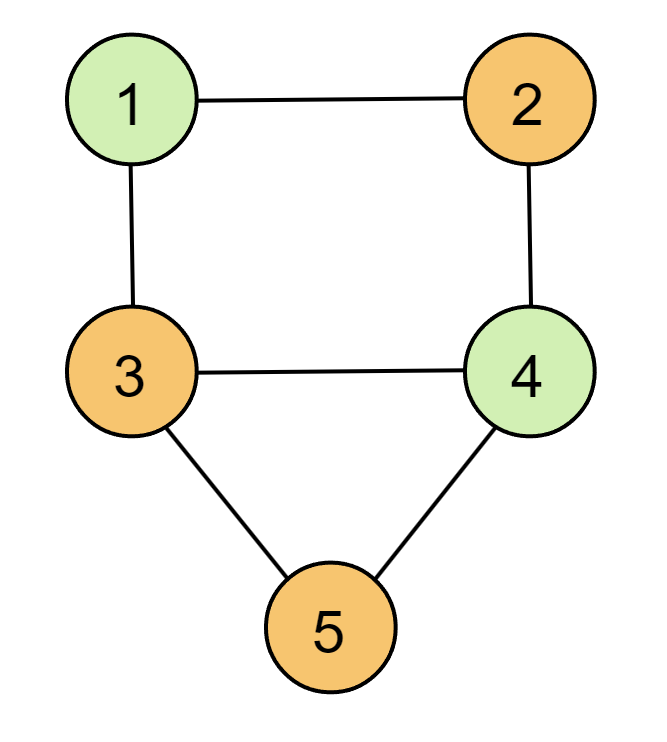
容易验证，在该解下所有惩罚函数均为0。

惩罚法的优缺点

优点

• 简单易实现：惩罚法通过将约束转化为惩罚项，避免了直接求解带约束的优化问题，计算过程相对简单，仅需将约束改写为二次惩罚项，即可直接映射到伊辛模型进行求解；
• 灵活性强：惩罚因子作为可调节的超参数，为不同场景提供弹性控制：
  • 对于硬约束（如电路设计中的物理连接限制），可采用指数增长的动态惩罚策略；
  • 对于软约束（如资源分配的偏好条件），可设置渐进式惩罚因子。这种灵活性在混合整数规划问题中尤为突出，例如在物流路径优化中，时间窗约束与运输成本可通过差异化的惩罚因子实现多目标权衡。
• 适应性好：惩罚法可以处理各种类型的约束，比如不等式约束、等式约束及逻辑约束。

缺点

• 惩罚因子选择困难：惩罚因子的选择对求解结果影响较大。如果选择不当，可能导致约束无法得到充分满足，或者目标函数过于偏离原始目标；
• 可能导致收敛性问题：在某些情况下，如果惩罚因子设置过大，优化过程可能会过于关注约束的满足，而忽视了目标函数的最小化，导致算法收敛到一个不理想的解；
• 可能产生不精确的解：由于惩罚法是间接处理约束，优化过程可能会得到一个不完全满足约束的解，尤其是在惩罚因子较小的情况下。

结论

惩罚法是处理QUBO模型中约束问题的常见方法，通过引入惩罚项，可以有效地将约束条件转化为目标函数的一部分。对于不等式约束，惩罚法通过引入松弛变量来允许部分违约，并通过惩罚项对违约进行惩罚；对于等式约束，惩罚法通过直接在目标函数中加入约束违背的平方惩罚项来确保等式满足。惩罚法的优势在于其简单性和灵活性，但在应用时需要谨慎选择惩罚因子，以避免可能的收敛性问题。

总体而言，惩罚法是一种简单有效的处理约束的技术，适用于多种实际优化问题。