案例解析：均衡传播算法

均衡传播算法借鉴生物神经网络的局部学习规则，通过模拟大脑突触的双阶段动态平衡，使玻尔兹曼机等能量模型摆脱传统对比散度的低效束缚。这种“神经动力学+概率建模”的耦合，不仅为生成式AI提供了更接近生物学习范式的训练框架，更在量子退火硬件上展现出指数级加速潜力，有望推动更高效、节能的神经计算硬件的发展。

本节将以均衡传播算法为例，讲述量子计算在人工智能领域的应用与创新。

附视频讲解： 均衡传播与CIM驱动的神经网络创新应用

1. Ising模型

1.1 伊辛模型的基本概念

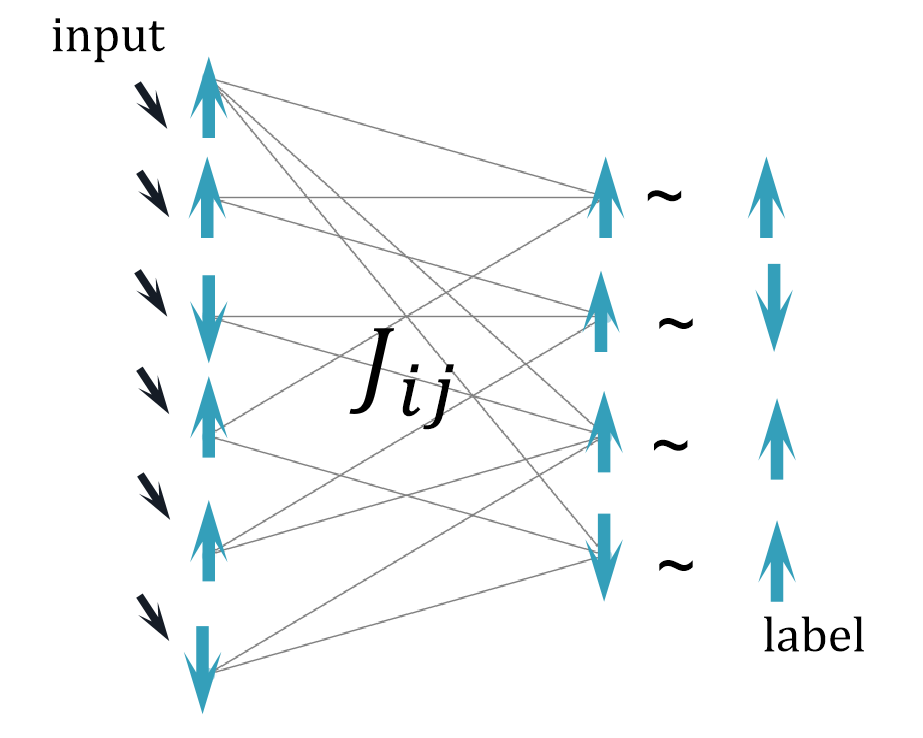
Ising模型最初是为解释铁磁相变现象提出的经典物理模型。其核心结构由二维晶格上的离散自旋系统构成：每个晶格节点$i$（$i=1,2,3,...$）具有±1两种自旋状态，相邻节点间通过耦合权重$J_{ij}$连接。系统总能量可表示为：$H=-\sum _{i,j}{J}_{ij}{s}_i{s}_j$，其中求和范围覆盖所有连接节点对。

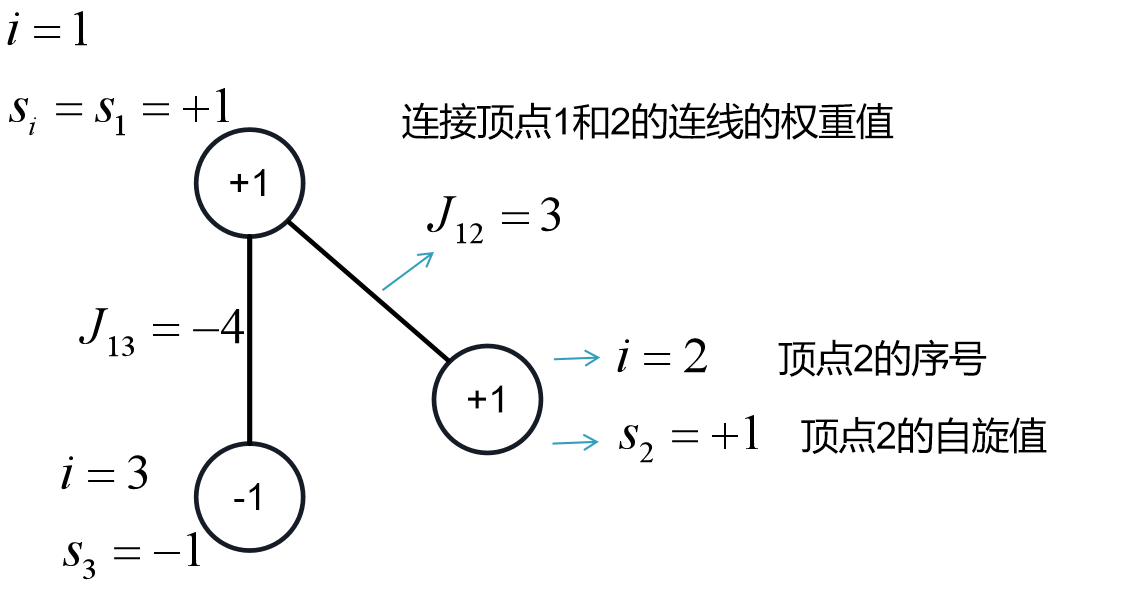
以图示的三节点系统为例：节点$s_1$与$s_2$、$s_1$与$s_3$分别通过权重为2和5的边连接，当自旋状态分别为$(+1,+1,-1)$时，系统总能量计算为：

$$\begin{array}{rl}H& =-\sum _{i,j}{J}_{ij}{s}_i{s}_j=-J_{12}{s}_1{s}_2-J_{13}{s}_1{s}_3\\ & =-3\cdot (+1)\cdot (+1)-(-4\cdot (-1)\cdot (+1))\\ & =-7\end{array}$$

1.2 伊辛模型与神经网络

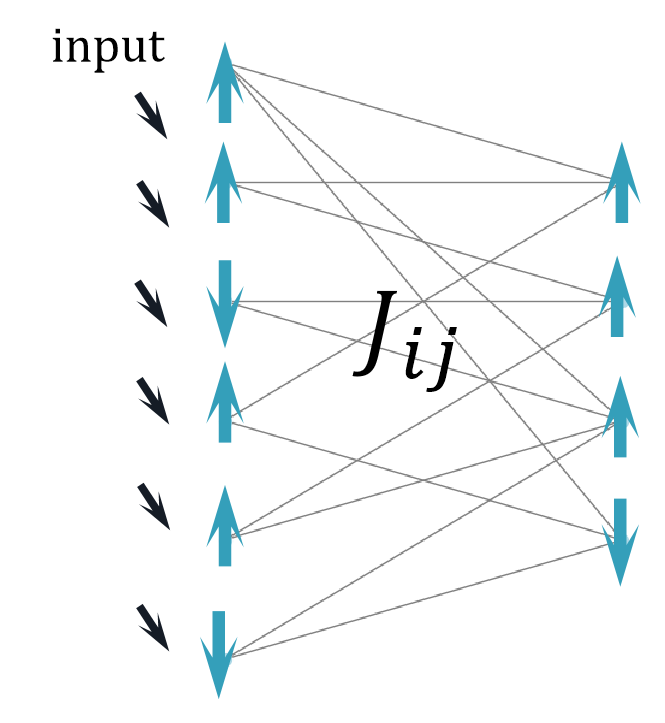
Ising模型是一个有着广泛应用的模型，我们来看一下它和神经网络之间的一些联系。Ising模型的自旋演化机制与神经网络神经元更新规则存在深刻关联。在Ising系统中，相邻自旋通过耦合作用相互影响：

$$H(\sigma )=-\sum _{i,j}{J}_{ij}{\sigma }_i{\sigma }_j-\mu \sum _i{h}_i{\sigma }_i$$

当耦合系数$J_{ij}>0$时，系统倾向于使相邻自旋方向一致（铁磁耦合）；当$J_{ij}<0$时则促使自旋方向趋于相反（反铁磁耦合）。系统会逐渐演化到平衡态，这个过程中系统能量会降低。而对于神经网络而言，神经元的更新规则类似于自旋的演化：

$$f_Q(x)=\sum _{i⩽j}{q}_{ij}{x}_i{x}_j$$

若输入神经元激活值为$+1$且连接权重为正，则该信号将促使下游神经元趋向正激活状态。以水果分类任务为例，构建包含重量、颜色两个输入特征，隐藏层及苹果/橘子输出层的神经网络。该网络通过层级连接权重计算特征组合，最终实现分类决策。值得注意的是，这种网络拓扑结构既可表征传统神经网络，也可映射为Ising模型的晶格结构，揭示了两者在计算本质上的相通性。

实际上，Ising模型的求解是很困难的，属于NP-hard组合优化问题，传统算法面临指数级复杂度挑战。本文后面将详细讨论Ising模型的高效求解方案——相干伊辛机（Coherent Ising Machine, CIM）。2018年《Science》报道的CIM突破性研究显示，CIM的光学计算架构在求解2000自旋问题时，速度较经典模拟退火算法提升近两个数量级，为复杂优化问题提供了物理计算的新的解决方案。

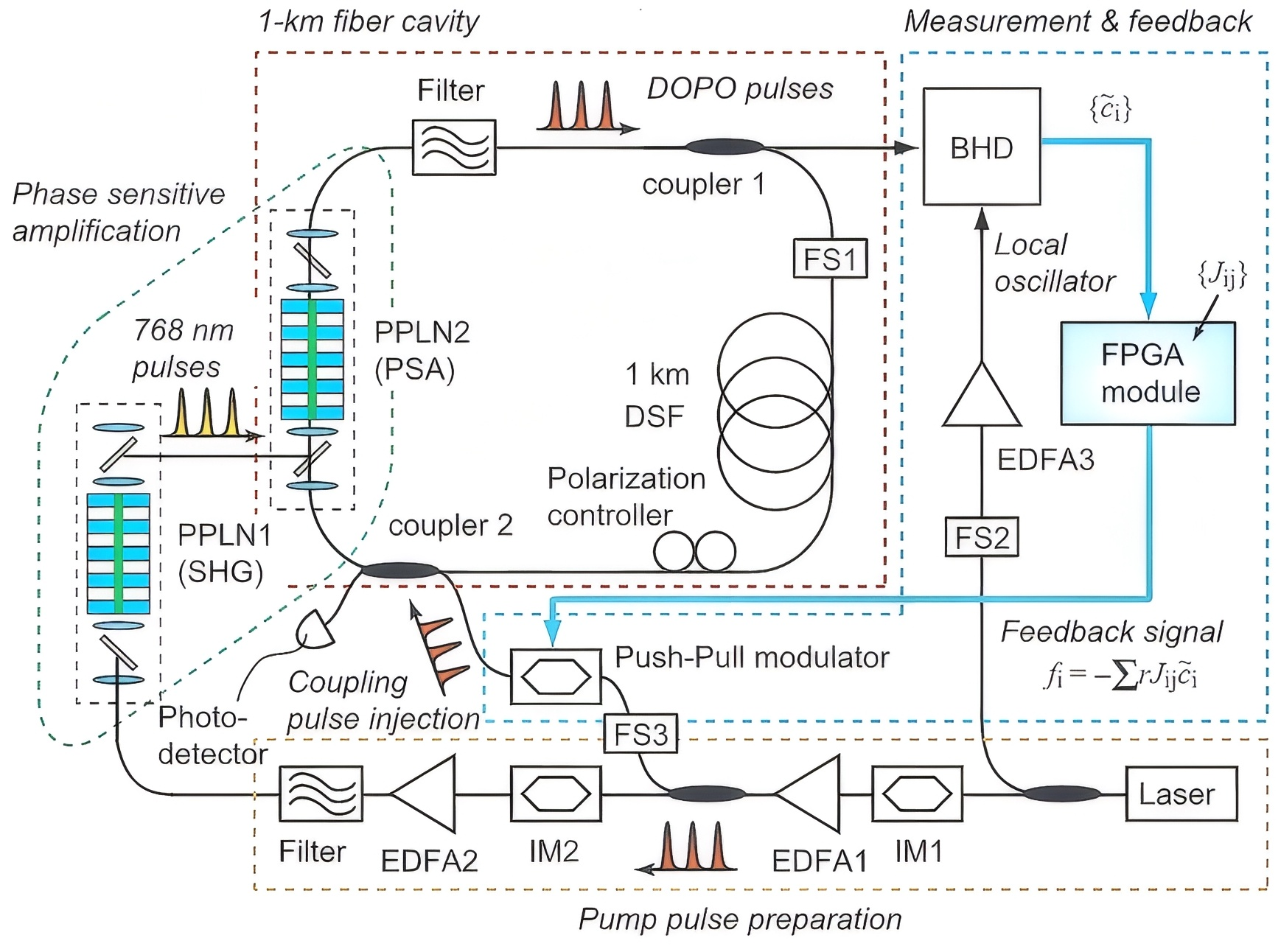
2. 均衡传播

2.1 均衡传播与反向传播

为深入理解均衡传播(Equilibrium Propagation, EP)的创新性，需系统对比其与传统反向传播(Backpropagation, BP)的算法差异。传统反向传播算法需要构建完整的计算图，通过链式法则将输出端的误差信号逐层逆向分解，每个神经元的权重更新都严格依赖于后续层的梯度信息：给定损失函数$L(\theta )=𝔼[\ell (f_{\theta }(x),y)]$，其梯度计算遵循$\partial L/\partial \theta =\partial \ell /\partial f_{\theta }·\partial f_{\theta }/\partial \theta$。

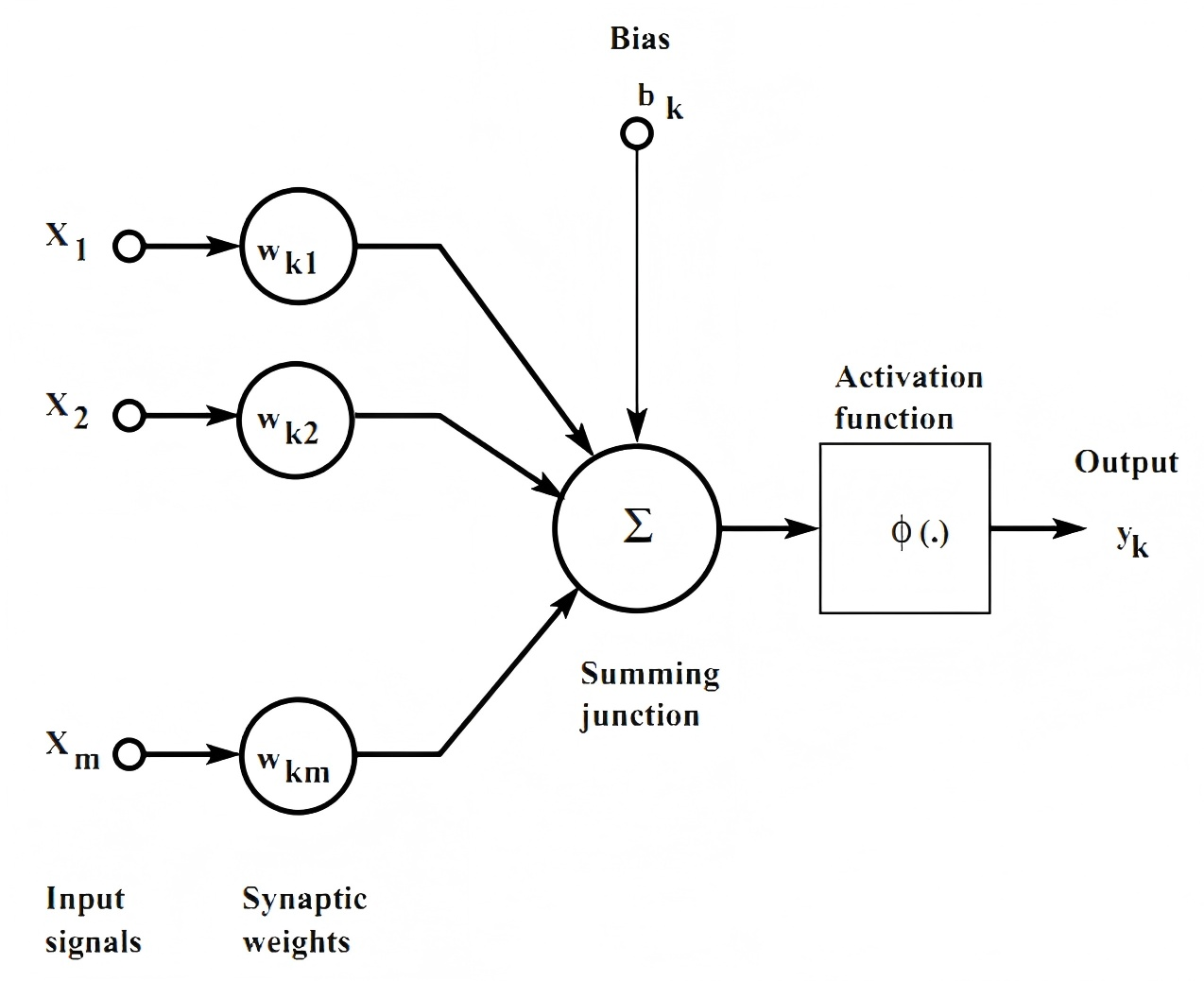
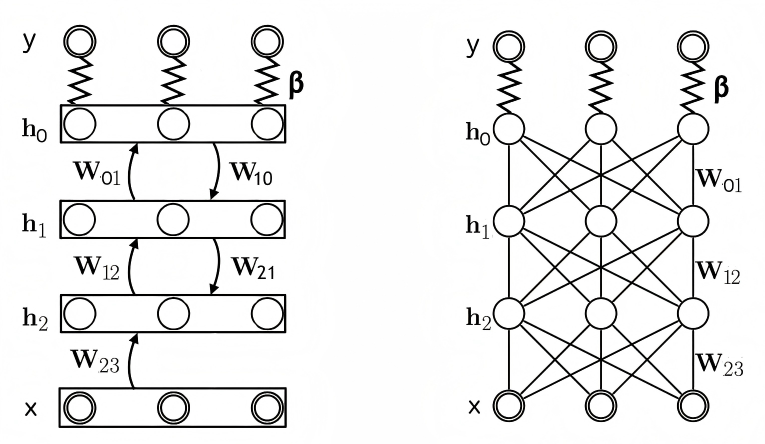
与反向传播相比，均衡传播具有如下图所示的优势。均衡传播建立在能量基模型(Energy-Based Models, EBMs)框架下，将网络视为动态系统，其状态演化由能量函数$E(s,\theta )$驱动，最终收敛于能量极小点$s\ast =argmi{n}_{s}E(s,\theta )$。在能效比和硬件友好性方面，均衡传播均表现优异，而且这种只依赖局部信息的学习规则，和我们的真真实实的人类神经更加符合。

2.2 均衡传播的训练过程

均衡传播的训练过程主要分为四个阶段：初始化参数、自由阶段、约束阶段和更新权重阶段。

（1）初始化参数： 网络由节点（神经元或自旋变量）和连接权重构成，节点状态$s_i\in \{-1,+1\}$表示激活状态，权重$J_{ij}$定义节点间的相互作用强度。初始，权重$J_{ij}$随机赋值，输入层节点固定为数据$x$，输出层目标为$y$。

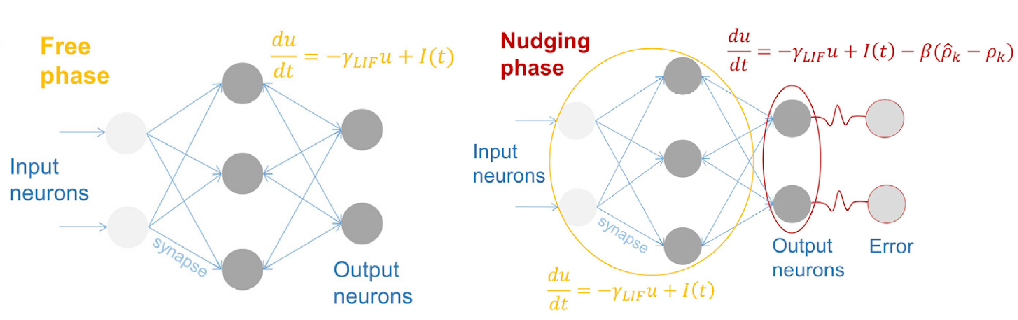
（2）自由阶段(Free Phase)： 系统在输入数据$x$驱动下自发演化至平衡态。此阶段能量函数仅包含网络内部相互作用，不进行约束也没有任何标签输入：

$$E_{\theta }(s)=-\sum _{i<j}{J}_{ij}{s}_i{s}_j-\sum _i{b}_i{s}_i$$

节点状态遵循梯度动力学方程：

$$\frac{d{s}_i}{dt}=-\frac{\partial E_{\theta }}{\partial s_i}=\sum _j{J}_{ij}{s}_j+b_i$$

当 $t\to \mathrm{\infty }$ 时，系统收敛至稳态 $s^0$，此时输出层 $s_Y$为网络对输入$x$的自然响应（无监督预测）。该阶段演化过程如下图所示：

（3）引导阶段(Nudge Phase)： 在自由阶段基础上，对输出层施加目标导向的约束，修正能量函数：

$$E_{\theta }^{\beta }(s)=E_{\theta }(s)+\beta C(s_Y,y)$$

其中约束项$C(s_Y,y)=\frac{1}{2}\sum _{i\in Y}(s_i-y_i{)}^2$将输出层节点$s_Y$拉向目标标签$y$。对其计算梯度可得：

$$\frac{\partial E_{\theta }^{\beta }}{\partial s_i}=\frac{\partial E_{\theta }}{\partial s_i}+\beta \frac{\partial C}{\partial s_i}$$

因此，其动力学方程为：

$$\frac{d{s}_i}{dt}=-\frac{\partial E_{\theta }^{\beta }}{\partial s_i}=-\frac{\partial E_{\theta }}{\partial s_i}-\beta \frac{\partial C}{\partial s_i}=\{\begin{array}{ll}\sum _j{J}_{ij}{s}_j+b_i& ,i\notin Y\\ \sum _j{J}_{ij}{s}_j+b_i+\beta (y_i-s_i)& ,i\in Y\end{array}$$

参数$\beta >0$控制目标约束强度。系统演化至新平衡态$s^{\beta }$，输出层被“牵引”至目标$y$。值得注意的是，由于隐层节点的反向传播效应，输入层状态也会发生适应性调整，也即模型的全网络协同优化特性。该阶段演化过程如下图所示：

（4）参数更新： 通过对比两阶段的差异，计算梯度：

$$\mathrm{\Delta }{J}_{ij}\propto -\frac{1}{\beta }(s_i^{\beta }{s}_j^{\beta }-s_i^0{s}_j^0)$$

此规则仅依赖相邻节点的状态乘积差异，符合局部学习特性。权重更新方向使约束项$C(s_Y,y)$最小化，推动网络输出逼近目标。理论分析表明（Scellier et al.,2022），当约束强度$\beta$和参数更新步长$\epsilon$满足$\epsilon ,\beta \to 0$时，更新量收敛于传统梯度：

$${\theta }_t={\theta }_{t-1}-\epsilon \beta {\mathrm{\nabla }}_{\theta }C(s({\theta }_{t-1},x_t),y_t)+O({\epsilon }^2\beta +\epsilon {\beta }^2)$$

也就是说，尽管均衡传播仅利用局部信息，其梯度方向与反向传播的全局梯度一致，但规避了链式求导的计算开销。

数学注记： 上述结论源于对扩展能量泛函

$$\mathcal{E}(u,\theta ,s,x,y,\epsilon ,\beta )=\frac{\parallel u-\theta {\parallel }^2}{2\epsilon }+E(\theta ,x,s)+\beta C(s,y)$$

的优化过程，通过交替求解

$$\begin{array}{rl}{\theta }_{\iota -1}& =\underset{\theta }{\arg min}\underset{s}{min}\mathcal{E}(u_{\iota },\theta ,s,x_{\iota },y_{\iota },\epsilon ,0)\\ {\theta }_t& =\underset{\theta }{\arg min}\underset{s}{min}\mathcal{E}(u_t,\theta ,s,x_t,y_t,\epsilon ,\beta )\end{array}$$

可导出参数更新量与损失函数梯度的一致性关系。

3. 均衡传播与CIM

3.1 借助CIM实现均衡传播

将均衡传播映射到CIM硬件实现时，需解决连续梯度与离散状态的适配问题。CIM通过物理系统的稳态演化实现均衡传播（EP）：耦合权重${\theta }_{ij}$作为可训练参数保持连续值域，支持梯度更新；而神经元状态$s_i$在CIM实现中被离散化为$\pm 1$（CIM通过$0/\pi$相位编码），但在微分方程框架下可保留连续激活值。这种特性使算法在硬件部署时利用二值状态的高能效特性，同时在软件仿真时保持传统神经网络的表达能力。 梯度计算通过自由阶段（$s^0$）与扰动阶段（$s^{\beta }$）的状态差异实现，具体公式为：

$$\mathrm{\Delta }{\theta }_{ij}\propto \frac{s_i^0{s}_j^0-s_i^{\beta }{s}_j^{\beta }}{\beta }$$

其中$\beta$为输出约束强度。以CIM为例，每个光学参量振荡器对应神经元，其振荡相位编码$\pm 1$状态。训练过程通过马赫-曾德尔干涉仪调制耦合强度：自由阶段锁定输入光子模式记录稳态相位$s^0$，扰动阶段注入调控光强诱导新平衡态$s^{\beta }$，梯度通过光电探测器测量两阶段外积差异并反馈更新权重。

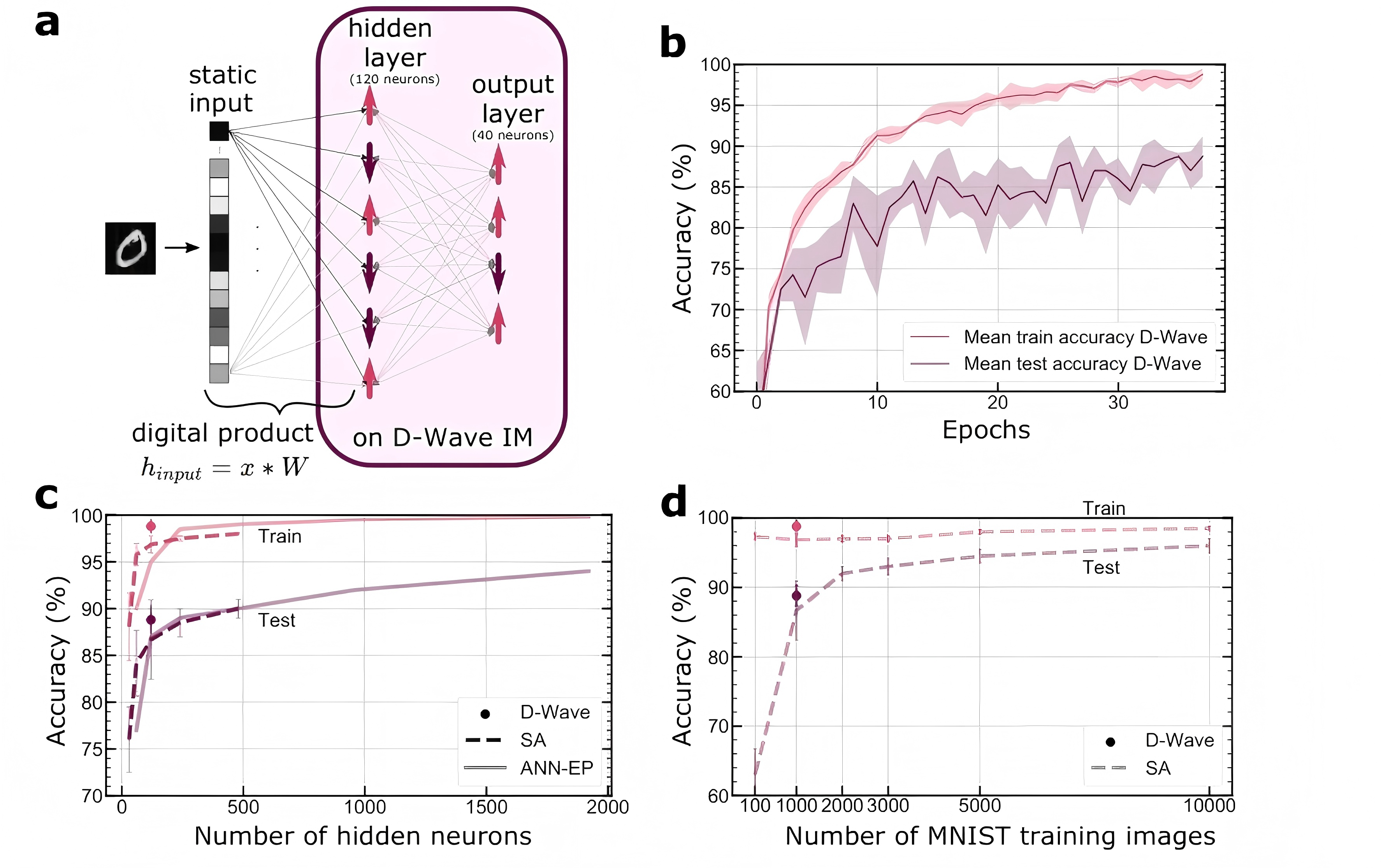
在CIM硬件上实现均衡传播的实证研究中，我们构建了面向MNIST手写数字识别的专用架构。输入层采用28×28=784个光学参量振荡器，其相位状态直接编码图像像素强度（$+1$对应墨迹区域，$-1$表示空白）。隐层设置120个可调谐耦合节点，输出层创新性地采用40节点扩展编码方案——每个数字类别分配4个节点，通过多数表决机制提升分类鲁棒性。实验采用1000个训练样本和100个测试样本的子集，在CIM平台上完成端到端训练。结果显示训练集准确率达98%，测试集准确率为88%，性能差距主要源于训练数据规模限制。值得注意的是，当输出约束强度$\beta =0.1$时，单次参数更新耗时仅3.2ms，较同等规模GPU训练提速约200倍。

3.2 伊辛模型与玻尔兹曼机

玻尔兹曼机（BM）与均衡传播（EP）均以能量最小化为核心范式，但其建模目标与实现路径存在本质差异。玻尔兹曼机的概率分布定义为：

$$p(v,h)=\frac{1}{Z}{e}^{-E(v,h)},E(v,h)=-\sum _{i,j}{w}_{ij}{v}_i{h}_j-\sum _i{a}_i{v}_i-\sum _j{b}_j{h}_j$$

其中可见层$v$与隐藏层$h$的状态服从概率分布，训练目标为最大化可见层数据的对数似然：

$$\arg max\sum _{x\in \mathcal{D}}\log p(x)$$

这一过程通过调整能量曲面使训练样本处于低能谷，本质上属于无监督特征学习。与之对比，均衡传播则构建监督学习导向的能量函数：

$$E(s)=\sum _{i<j}{\theta }_{ij}{s}_i{s}_j+\sum _i{b}_i{s}_i+\beta \parallel s_{\text{out}}-y{\parallel }^2$$

其中$\beta$项引入目标导向的约束势场，其训练通过自由阶段（$\beta =0$）与引导阶段（$\beta >0$）的平衡态差异生成确定性梯度：

$$\mathrm{\Delta }{\theta }_{ij}\propto \frac{1}{\beta }(s_i^0{s}_j^0-s_i^{\beta }{s}_j^{\beta })$$

二者的核心区别体现在：

维度	玻尔兹曼机	均衡传播
学习范式	无监督生成模型	监督学习框架
梯度估计	概率采样（MCMC）	确定性平衡态差异
硬件适配性	需高温退火（模拟退火）	直接利用Ising机基态搜索

3.3 实验架构与结果

本部分使用MNIST进行伊辛机实现均衡传播的实证研究。MNIST 数据集是机器学习和深度学习领域中最经典的基准数据集之一，由 Yann LeCun 等研究者于 1998 年创建，包含60,000个训练样本和10,000个测试样本，主要用于手写数字识别任务。每个样本是28×28像素的灰度图像，对应0到9的数字类别。

针对MNIST/100的子集（1000训练样本，100测试样本）构建专用架构：

• 输入层：28×28=784个光学参量振荡器，相位编码像素强度（$+1$为墨迹，$-1$为空白）；
• 隐层：120个可调谐耦合节点；
• 输出层：40节点扩展编码（每数字类别分配4节点）。

实验结果表明，EP算法在训练集上达到了98.8% 的准确率，在测试集上达到了88.8% 的准确率。

4. 应用与展望

4.1 均衡传播的应用

均衡传播（EP）的发展深度融合了硬件创新与算法优化，已经在跨学科领域展现独特优势。

图片生成 ：结合均衡传播（EP）和Hopfield网络的变分自编码器（VAE）训练，用于生成建模任务研究利用Hopfield网络的对称性，设计了一个模型同时作为编码器和解码器。实验表明，该方法在生成图像质量上与传统反向传播训练的VAE相当。

神经网络模拟：均衡传播被用于训练脉冲神经网络（SNN），这是一种更接近生物神经网络的计算模型，将脉冲信号与能量最小化相结合。基于均衡传播的权重更新表现出尖峰时间依赖性可塑性（STDP），与生物学机制相契合。

4.2 均衡传播的展望

均衡传播（EP）作为一种基于物理系统的机器学习范式，其核心优势在于通过硬件与算法的深度协同实现高效训练。

在硬件加速领域，未来可进一步探索与光子、超导量子比特等新型计算架构的结合，突破传统冯・诺依曼瓶颈。

跨学科应用方面，EP的能量最小化机制与物理系统的自组织特性高度契合，可扩展至化学分子结构优化、热力学系统相变预测等领域。例如，在生物医学中，通过构建蛋白质相互作用的Ising模型，EP可高效求解蛋白质折叠问题，其离散状态特性恰好匹配生物分子的二态性特征，有望推动交叉学科的突破性进展。

算法改进层面，当前EP在梯度计算中依赖两阶段状态差异的近似（$\mathrm{\Delta }{\theta }_{ij}\propto (s_i^0{s}_j^0-s_i^{\beta }{s}_j^{\beta })/\beta$），未来可引入动态$\beta$调节策略以平衡训练稳定性与收敛速度。同时，结合连续激活值的微分方程框架，探索离散-连续混合训练模式，既能保留硬件优势，又可提升复杂任务的表达能力。