4.3 处理降次问题

背景介绍

前面也有学习过，QUBO二次无约束二元优化的目的是求得一组布尔变量的值

(x_{0}, x_{1} \dots x_{n})

使得二阶多项式

x^{T} Q x

的值最小。

然而，实际应用中，经常会遇到三次或更高次数的多项式问题，这些高阶项不能直接用QUBO求解。为了解决这个问题，我们引入了HOBO（Higher Order Binary Optimization）模型，它可以通过引入辅助变量和额外的约束，将高阶项转换为低阶二次项来实现优化。

高阶问题降阶的流程如下图所示，下一小节将具体介绍高阶降次的具体方法与相应的Kaiwu SDK的用法。

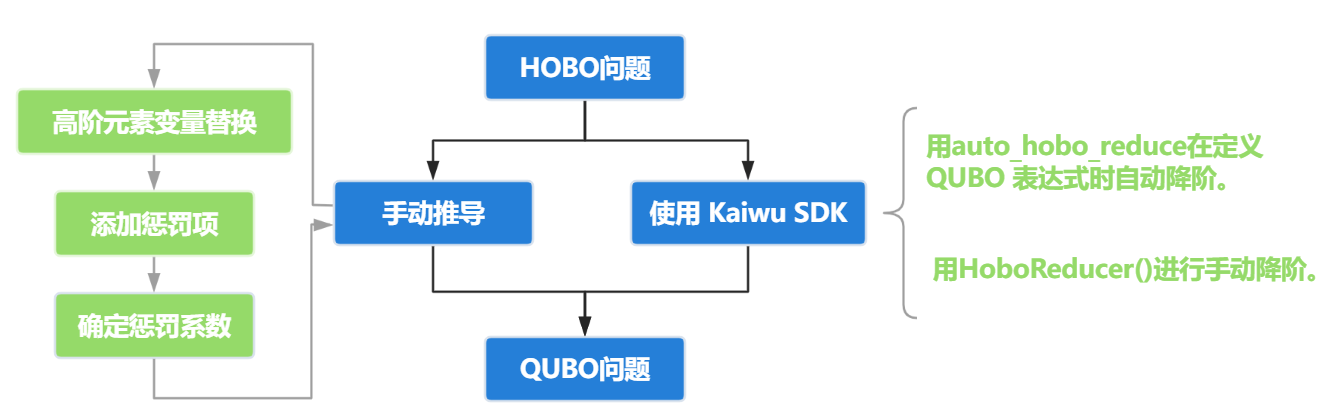
高阶降次方法

（1）HOBO模型

一般的HOBO问题可以定义为：

f (x) = \sum_{i_{1}, i_{2}, \dots, i_{k}} a_{i_{1} i_{2}, \dots, i_{k}} x_{i_{1}} x_{i_{2}}, \dots x_{i k}

其中 $x = (x_{1}, x_{2}, \dots, x_{n})$ 的每个 $x_{i}$ 都是一个可以取值为 $0$ 或 $1$ 的布尔变量， $k$ 表示多项式的阶数， $k > 2$ 。HOBO问题可以有约束项，带约束的问题同样可以通过添加惩罚项的方式转换为无约束问题。

HOBO模型在需要考虑复杂关系和高阶相互作用的领域，如机器学习、金融、物流和数论等，均有应用。应用HOBO模型解决上述问题时，模型中的高阶项可以对这些问题中的约束和固有关系进行更为详细的数学描述。

（2）将HOBO问题转化为 QUBO问题

HOBO问题的目标也是最小化目标函数 $f (x)$ 。然而，CIM被设计用于处理二次模型。因此，HOBO模型通常通过引入辅助变量和额外的约束来将其转换为QUBO模型，以将高阶项分解为二次项。

首先，把两个变量的乘积用一个变量替代，例如令

y = x_{0} x_{1}

并代入原式，将原式中的单项式阶数降低，并且添加

y = x_{0} x_{1}

的约束。

而要使得约束成立的方式是在原式中添加惩罚项，即Rosenberg二次惩罚项，

p (x_{0}, x_{1}, y) = x_{0} x_{1} - 2 x_{0} y - 2 x_{1} y + 3 y

该惩罚项是如此形式，是为了满足如下要求：

p (x_{0}, x_{1}, y) {\begin{matrix} = 0 ， y = x_{0} x_{1} \\ > 0 ， y \neq x_{0} x_{1} \end{matrix}

对所有的高阶项都进行如上处理后，就得到最终新的多项式为

f (x, y) + k \sum p (x_{i}, x_{j}, y_{i j})

其中 $k$ 是惩罚项系数。

（3）举例说明

这里举一个例子来展示这种降次方式。

例如我们有

\begin{matrix} (1) & H = x_{1} - x_{1} x_{2} x_{3} \end{matrix}

然后按下述方式转化为无约束二次型。

步骤1 变量替换

首先把两个变量的乘积用一个变量替换，这里我们用 $y$ 替换$ x*{2}x*{3} $，于是有：

\begin{matrix} (2) & H = x_{1} - x_{1} y \end{matrix}

于是变量替换也成为一个要满足的约束条件，即有新的约束条件：

\begin{matrix} (3) & y = x_{2} x_{3} \end{matrix}

步骤2 加入惩罚项

现在目标函数的阶数下降了，但是新增了约束项，这就回到了4.1学习的内容范畴了。前面我们学习过，我们的目的是计算目标函数的最小值，那么我们可以在目标函数上增加一个非负的惩罚函数，使其满足新的约束条件。下面我们来看这种惩罚项怎么构造。

设上面的约束对应的惩罚项为 $H^{'}$ 。

则 $x_{2}$ 、 $x_{3}$ 和 $y$ 可以构成的二次多项式可以设为如下的形式：

\begin{matrix} (4) & H^{'} = a x_{2} + b x_{3} + c y + d x_{2} x_{3} + e x_{3} y + f x_{2} y \end{matrix}

步骤3 寻找合适的多项式系数

因为 $H^{'}$ 是一个非负的惩罚项，所以只要它在满足 $y = x_{2} x_{3}$ 时有 $H^{'} = 0$ ，在不满足条件时有 $H^{'} > 0$ ，就能起到惩罚函数的作用。

即令

\begin{matrix} (5) & H^{'} (x_{2}, x_{3}, y) {\begin{matrix} = 0 ， y = x_{2} x_{3} \\ > 0 ， y \neq x_{2} x_{3} \end{matrix} \end{matrix}

显然， $(0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 1)$ 都是满足公式（3）的 $(x_{2}, x_{3}, y)$ 的组合。将这些组合代入，则有：

\begin{matrix} (6) & {\begin{aligned} b & = 0 \\ a & = 0 \\ a + b + c + d + e + f & = 0 \end{aligned} \end{matrix}

而在不满足（3）时，我们把 $(x_{2}, x_{3}, y)$ 的组合 $(0, 0, 1), (0, 1, 1), (1, 0, 1), (1, 1, 0)$ 代入（4）和（5）可以得到：

\begin{matrix} (7) & {\begin{aligned} c & = k_{1} \\ c + e & = k_{2} \\ c + f & = k_{3} \\ d & = k_{4} \end{aligned} \end{matrix}

其中， $k_{1}, k_{2}, k_{3}, k_{4} > 0$ 。

接下来就是给 $(k_{1}, k_{2}, k_{3}, k_{4})$ 寻找合适的赋值。经过尝试发现如下的取值可以满足约束：

\begin{matrix} (8) & (k_{1}, k_{2}, k_{3}, k_{4}) = (3, 1, 1, 1) \end{matrix}

对应的 $(a, b, c, d, e, f)$ 为：

\begin{matrix} (9) & (a, b, c, d, e, f) = (0, 0, 3, 1, - 2, - 2) \end{matrix}

最终得到惩罚项

\begin{matrix} (10) & H^{'} = 3 y + x_{2} x_{3} - 2 x_{3} y - 2 x_{2} y \end{matrix}

这种惩罚项也被称为Rosenberg二次惩罚项。

步骤4 获得最终的无约束二次多项式模型

于是最终新的多项式为

\begin{matrix} (11) & H + k H^{'} = x_{1} - x_{1} y + k (3 y + x_{2} x_{3} - 2 x_{3} y - 2 x_{2} y) \end{matrix}

其中 $k$ 为惩罚系数。在确定惩罚系数后，就能得到如下的QUBO矩阵：

\begin{matrix} (12) & Q U B O = (\begin{array}{cccc} 1 & 0 & 0 & - 1 \\ 0 & 0 & k & - 2 k \\ 0 & 0 & 0 & - 2 k \\ 0 & 0 & 0 & 3 k \end{array}) \end{matrix}

于是我们实现了多项式的降阶并得到了对应的QUBO模型。

使用Kaiwu SDK进行高阶多项式的降次

在 Kaiwu SDK 中，提供了自动和手动两种降阶工具，帮助用户将高阶优化问题转换为QUBO问题，避免繁杂的手动计算过程。

用户可以用kw.qubo.QuboExpression.auto_hobo_reduce在定义 QUBO 表达式时自动将高阶项降阶为二次项；也可以用kw.qubo.HoboReducer()进行手动降阶。

下面进行函数的详细说明与应用实例。

（1）注意事项

新变量为原变量名字用下划线相连，如 x0 和 x1 被替换为 _x0_x1，_x0_x1 和 _x0_y1 被替换为 _x0_x1_y1

_ 是内部保留符号，不对用户开放用于命名变量。

（2）函数说明

kw.qubo.QuboExpression.auto_hobo_reduce
该函数用于控制是否在创建 QUBO 表达式时自动进行高阶项降阶。
如果希望在定义 QUBO 表达式时自动将高阶项简化为二次项，可以设置 auto_hobo_reduce = True。否则可以设置 auto_hobo_reduce = False，并且手动使用 HoboReducer 类来完成降阶。
kw.qubo.HoboReducer()
手动降阶的工具类，将高阶表达式简化为 QUBO 表达式。可以完成建模后，进行QUBO表达式的降阶。
kw.qubo.hobo_verify()
验证求得的解是否满足 HOBO 降阶的约束条件。

（3）使用举例

方法1 计算后降阶

计算后降阶是在关闭自动降阶功能后，手动使用 HoboReducer 类来完成降阶。

如下是一个将 y1 和 y2 相乘生成的高阶表达式 y3手动降阶高阶项，生成QUBO 表达式 y4的例子。

python

import numpy as np
import kaiwu as kw

kw.qubo.QuboExpression.auto_hobo_reduce = False
x = kw.qubo.ndarray(10, "x", kw.qubo.Binary)
y1 = x[0]*x[1] + x[2]*x[3] + x[8]
y2 = x[3]*x[4] + x[5]*x[6] + x[7]
y3 = y1 * y2
print(y3, "\n")
reducer = kw.qubo.HoboReducer()
y4 = reducer.reduce(y3)
kw.qubo.details(y4)

执行以上代码后结果为

python

x[2]*x[3]*x[5]*x[6]+x[2]*x[3]*x[3]*x[4]+x[2]*x[3]*x[7]+x[0]*x[1]*x[5]*x[6]+x[0]*x[1]*x[3]*x[4]+x[0]*x[1]*x[7]+x[5]*x[6]*x[8]+x[3]*x[4]*x[8]+x[7]*x[8]

QUBO Details:
Variables(Binary):_x[0]_x[1], _x[2]_x[3], _x[3]_x[4], _x[5]_x[6], x[4], x[7], x[8]
QUBO offset:      0
QUBO coefficients:
    _x[2]_x[3], _x[5]_x[6] : 1
    _x[2]_x[3], x[4]       : 1
    _x[2]_x[3], x[7]       : 1
    _x[0]_x[1], _x[5]_x[6] : 1
    _x[0]_x[1], _x[3]_x[4] : 1
    _x[0]_x[1], x[7]       : 1
    _x[5]_x[6], x[8]       : 1
    _x[3]_x[4], x[8]       : 1
    x[7], x[8]             : 1
HOBO Constraint:
    _x[5]_x[6] : x[5], x[6]
    _x[2]_x[3] : x[2], x[3]
    _x[0]_x[1] : x[0], x[1]
    _x[3]_x[4] : x[3], x[4]

在上面的结果中，

python

x[2]*x[3]*x[5]*x[6] + x[2]*x[3]*x[3]*x[4] + x[2]*x[3]*x[7] + x[0]*x[1]*x[5]*x[6] + x[0]*x[1]*x[3]*x[4] + x[0]*x[1]*x[7] + x[5]*x[6]*x[8] + x[3]*x[4]*x[8] + x[7]*x[8]

是原始的 HOBO 表达式。

形式如_x[i]_x[j] 的元素为 _x[i] 和 _x[j] 变量合并后的新变量。

最终的降阶 QUBO 表达式被表示为：

python

QUBO coefficients:
    _x[2]_x[3], _x[5]_x[6] : 1
    _x[2]_x[3], x[4]       : 1
    _x[2]_x[3], x[7]       : 1
    _x[0]_x[1], _x[5]_x[6] : 1
    _x[0]_x[1], _x[3]_x[4] : 1
    _x[0]_x[1], x[7]       : 1
    _x[5]_x[6], x[8]       : 1
    _x[3]_x[4], x[8]       : 1
    x[7], x[8]             : 1

这些系数表示了经过降阶后的 QUBO 表达式的各项，其中 _x[2]_x[3], _x[5]_x[6] : 1 表示两个二元变量 _x[2]_x[3] 和 _x[5]_x[6] 的组合的系数为 1，依此类推。

方法2 计算时降阶

auto_hobo_reduce = True能够开启自动降阶功能，创建 QUBO 表达式时自动将高阶项转化为二次项。

下面是一个自动降阶的例子，创建了更多的二进制变量 x1, x2, x3, y1, y2, y3，并定义了两个 QUBO 表达式 p1 和 p2，将p1 和 p2这两个表达式相乘，生成一个更复杂的 QUBO 表达式。

python

# auto_hobo_reduce defaults to True
kw.qubo.QuboExpression.auto_hobo_reduce = True

x1, x2, x3 = kw.qubo.Binary("x1"), kw.qubo.Binary("x2"), kw.qubo.Binary("x3")
y1, y2, y3 = kw.qubo.Binary("y1"), kw.qubo.Binary("y2"), kw.qubo.Binary("y3")
p1 = x1 * x2 + 2* y1 * y1
p2 = x1 * y1 + y3
result = p1 * p2
kw.qubo.details(result)

执行以上代码后得到降阶后的结果如下。

python

QUBO Details:
  Variables(Binary):_x1_x2, _x1_y1, y1, y3
  QUBO offset:      0
  QUBO coefficients:
    y1, y3         : 2
    _x1_y1, y1     : 2
    _x1_x2, y3     : 1
    _x1_x2, _x1_y1 : 1
  HOBO Constraint:
    _x1_y1 : x1, y1
    _x1_x2 : x1, x2

可以看到result 中的高阶项被转换为二次项，所有变量和系数都会被简化为 QUBO 表达式。

*检验求得的结果是否满足降阶约束条件

下面使用 hobo_verify 函数验证降阶后的 QUBO 解是否满足 HOBO 降阶约束。其中，p 是包含高阶项的 QUBO 表达式，{"x1": 1, "x2": 1, "x3": 0, "_x1_x2": 1} 是解的赋值，表示给定二进制变量的值。

hobo_verify 会检查解是否符合降阶后的约束条件，返回 err_cnt，如果 err_cnt 为 0，表示满足约束。

python

p = x1*x2*x3
err_cnt, result_dic = kw.qubo.hobo_verify(p, {"x1":1,"x2":1,"x3":0,"_x1_x2":1})
print(err_cnt)

得到结果为0，证明解满足降阶的约束。

1.1 量子计算介绍

1.2 相干光量子计算机

1.3 Ising（伊辛）模型＆QUBO模型

1.4 CIM求解组合优化问题过程

2.1 TSP实例教学

3.1 Kaiwu SDK

3.2 云服务&经典求解器

3.3 开源代码使用指南

3.4 新手教程

3.5 CIM求解组合优化问题的优势和方法

4.1 处理约束问题

4.2 调整惩罚系数

4.3 处理降次问题

5.1 适配参数精度（8bit整数）

5.2 量子＋经典算法

6.1 论文解读

量子＋运筹优化

生物制药

电力

6.2 优秀论文库

4.3 处理降次问题

背景介绍

高阶降次方法

（1）HOBO模型

（2）将HOBO问题转化为 QUBO问题

（3）举例说明

步骤1 变量替换

步骤2 加入惩罚项

步骤3 寻找合适的多项式系数

步骤4 获得最终的无约束二次多项式模型

使用Kaiwu SDK进行高阶多项式的降次

（1）注意事项

（2）函数说明

（3）使用举例

方法1 计算后降阶

方法2 计算时降阶

*检验求得的结果是否满足降阶约束条件

量子＋运筹优化

生物制药

电力

4.3 处理降次问题 ​

背景介绍 ​

高阶降次方法 ​

（1）HOBO模型 ​

（2）将HOBO问题转化为 QUBO问题 ​

（3）举例说明 ​

步骤1 变量替换 ​

步骤2 加入惩罚项 ​

步骤3 寻找合适的多项式系数 ​

步骤4 获得最终的无约束二次多项式模型 ​

使用Kaiwu SDK进行高阶多项式的降次 ​

（1）注意事项 ​

（2）函数说明 ​

（3）使用举例 ​

方法1 计算后降阶 ​

方法2 计算时降阶 ​

*检验 求得的结果是否满足降阶约束条件 ​

4.3 处理降次问题

背景介绍

高阶降次方法

（1）HOBO模型

（2）将HOBO问题转化为 QUBO问题

（3）举例说明

步骤1 变量替换

步骤2 加入惩罚项

步骤3 寻找合适的多项式系数

步骤4 获得最终的无约束二次多项式模型

使用Kaiwu SDK进行高阶多项式的降次

（1）注意事项

（2）函数说明

（3）使用举例

方法1 计算后降阶

方法2 计算时降阶

*检验求得的结果是否满足降阶约束条件