1.3 Ising（伊辛）模型＆QUBO模型

概念介绍

伊辛模型（Ising Model）的提出是为了解释统计物理学中的磁性物质相变现象，即磁铁临界温度以上出现磁性消失的现象，但后来发现可以扩展到其它很多自然和社会科学问题上，是统计物理学中唯一一个同时具备表述简单、内涵丰富、应用广泛这三种优点的模型，可以用来求解各种组合优化问题。抽象为数学形式为：

$$H(\sigma )=-\sum _{i,j}{J}_{ij}{\sigma }_i{\sigma }_j-\mu \sum _i{h}_i{\sigma }_i$$

其中$\sigma$为待求自旋变量，代表二进制决策变量，取值为$(-1,1)$；

$H$为哈密顿量；

$J$为二次项系数，是相互作用的系数，通常对称，即$J_{ij}＝J_{ji}$；

$\mu$和$h$为线性项系数，是已知量。

在数学上，求解Ising模型的基态能量是一个整数规划问题，属于NP-complete问题之一，这与组合优化问题就具有了相似之处。利用量子计算机解决组合优化问题，即是将这些问题转换为Ising模型，并通过以自旋方式运行的量子物理系统找到基态去求解问题，即系统中处于“最高效”集体振荡模式对应了给定Ising问题的最优解。

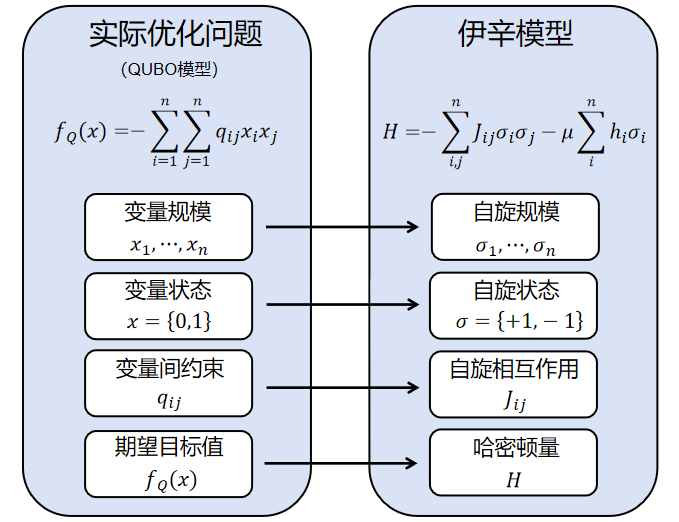伊辛模型与组合优化问题的对应关系

QUBO（Quadratic Unconstrained Binary Optimizatoin），无约束二次二进制优化模型，是如今量子计算中应用最广泛的优化模型，它统一了丰富多样的组合优化问题，通过量子计算机加速，可高效求解组合优化问题。同时QUBO模型可以表达位运算，进而表达各种逻辑，操作简便。

其表达式为：

$$f_Q(x)=\sum _{i=1}^n\sum _{j=1}^i{q}_{ij}{x}_i{x}_j$$

其中，$x_i$取值为$(0,1)$，是二进制决策变量（在QUBO中，变量为0或1，而不是-1和+1）；

$q_{ij}$为二次项的系数矩阵，描述不同变量间的相互作用。

QUBO问题是一个NP-Hard问题，对于理论计算机科学中的许多经典问题，如最大割、图着色和划分问题，都可以转化为QUBO问题。一些机器学习模型也可以Embedd到QUBO中，包括支持向量机、聚类和概率图形模型。此外，由于其与伊辛模型的密切联系，QUBO构成了绝热量子计算的核心问题类。

相互关系

QUBO和Ising模型在数学上有着密切的联系，且可以通过适当的变量映射和数学转换相互转化，它们本质上描述的是相似的二进制优化问题。QUBO模型更便于建模，Ising模型可以直接用于CIM（相干伊辛机）求解器进行求解。CIM利用光的经典特性通过优化Ising模型来解决QUBO问题，从而在组合优化问题中展现出强大的计算能力，可以在毫秒级别的时间内找到最优解。

在Ising模型中，每个变量表示的是一个二进制值（通常是+1或-1），代表了物理系统中的“自旋”方向。通常，为了与QUBO模型兼容，变量可以通过简单的映射转换为0和1。例如使用如下变量代换：

$$\begin{array}{rl}{\sigma }_i& =2x_i-1\\ x_i& =({\sigma }_i+1)/2\end{array}$$

这样，当$\sigma ＝1$时，$X_i=1$，当$\sigma =-1$时，$X_i=0$。

而QUBO模型每个变量取值为0或1，这使得在求解时更直接适用于许多优化算法，尤其是量子计算领域的优化方法。

CIM求解模型

CIM求解QUBO或优化Ising模型的过程就是将QUBO中的$q_{ij}$或Ising模型中的$J_{ij}$输入CIM中，CIM返回$x$或$\sigma$的过程。

进阶学习：如何应用QUBO模型来建模