5.1 适配参数精度（8bit整数）

教程一：直接应用于Ising矩阵算法

先前已经介绍过TSP的数学建模过程，本教程将演示如何使用python代码及Kaiwu SDK构建并求解旅行商问题（TSP），主要包括约束条件设置、精度控制及求解器配置，并提供完整代码示例。

1. 目标与约束构建

距离矩阵$w$: 表示节点间的邻接关系。

给定一个图：

w = np.array([[0, 0, 1, 1, 0],
			  [0, 0, 1, 0, 1],
			  [1, 1, 0, 0, 1],
			  [1, 0, 0, 0, 1],
			  [0, 1, 1, 1, 0]])

示例中为5个节点的无向图，5×5矩阵$w[u,v]$表示城市间连接关系，0表示无直接连接。

示例矩阵对应以下拓扑：

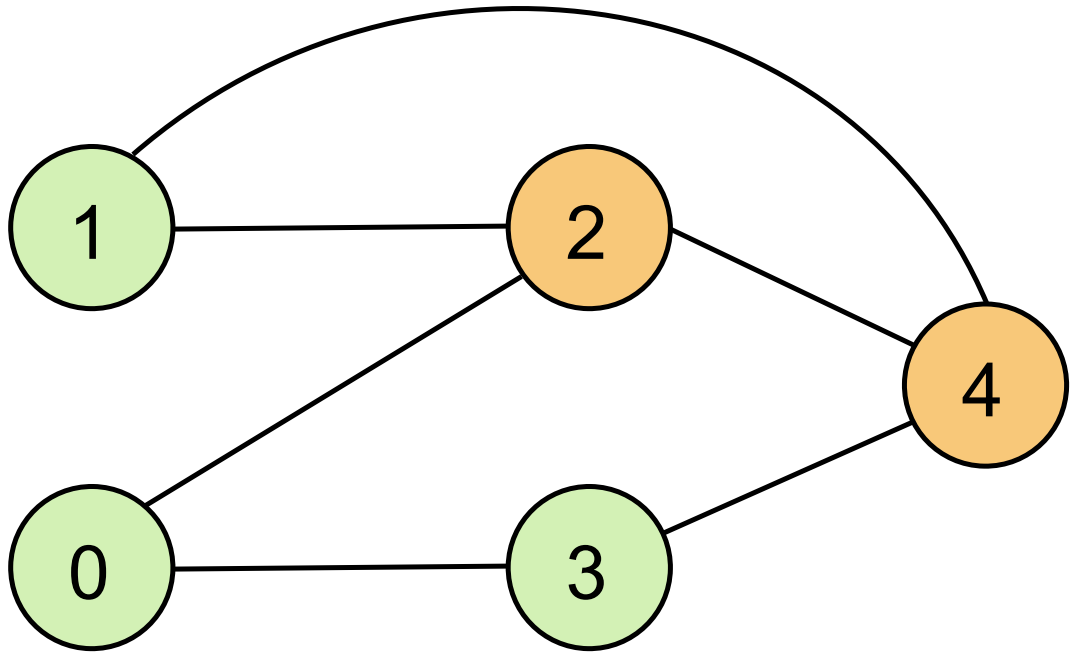城市连接

使用二维变量矩阵$x[u,i]$，表示城市$u$是否位于路径的第$i$个位置，其中$u$为城市编号（0-4），$i$为路径位置（0-4）。若$x[u,i]=1$，则表示城市$u$位于路径第$i$个位置，对于$n$个节点的问题，需要$n\times n$个二进制变量。

x = kw.qubo.ndarray((n, n), "x", kw.qubo.Binary)

目标是最小化路径总成本，即所有相邻城市间距离的和，数学表达式为：

$$\text{min}\sum _{(u,v)\in E}(w_{u,v}\cdot \sum _{j=0}^{n-1}{x}_{u,j}{x}_{v,(j+1)\mathrm{\%}n})$$

其中$E$是存在边的城市对集合，$\sum _{j=0}^{n-1}{x}_{u,j}{x}_{v,(j+1)\mathrm{\%}n}$表示边$(u,v)$是否被使用，函数is_edge_used判断边$(u,v)$是否出现在路径中：

def is_edge_used(x, u, v):
    return kw.qubo.quicksum([x[u, j] * x[v, (j + 1) % n] for j in range(n)])

path_cost = kw.qubo.quicksum([w[u, v] * is_edge_used(x, u, v) for u, v in edges])
qubo_model.set_objective(path_cost)

这个函数计算的是节点$u$在位置$j$且节点$v$在位置$j+1(modn)$的情况，确保边$(u,v)$确实被路径使用，需要满足三个主要约束：

（1）节点约束：每个城市必须出现在路径的某个位置

$$\sum _{j=0}^{n-1}{x}_{u,j}=1\mathrm{\forall }u\in \{0,\dots ,n-1\}$$

（2）位置约束：每个位置必须包含一个城市

$$\sum _{u=0}^{n-1}{x}_{u,j}=1\mathrm{\forall }j\in \{0,\dots ,n-1\}$$

（3）边约束：路径中不能包含不存在的边

$$\sum _{(u,v)\notin E}\sum _{j=0}^{n-1}{x}_{u,j}{x}_{v,(j+1)\mathrm{\%}n}=0$$

上面三个约束在代码中通过add_constraint方法添加，并均赋予惩罚系数5：

qubo_model.add_constraint(x.sum(axis=0) == 1, "node_cons", penalty=5)
qubo_model.add_constraint(x.sum(axis=1) == 1, "pos_cons", penalty=5)
qubo_model.add_constraint(
    kw.qubo.quicksum([is_edge_used(x, u, v) for u, v in no_edges]),
    "edge_cons", penalty=5
)

这样整个QUBO模型可以表示为：

$$\begin{array}{rl}H& =\sum _{(u,v)\in E}{w}_{u,v}\sum _{j=0}^{n-1}{x}_{u,j}{x}_{v,(j+1)\mathrm{\%}n}\\ & +P_1\sum _{u=0}^{n-1}{(1-\sum _{j=0}^{n-1}{x}_{u,j})}^2+P_2\sum _{j=0}^{n-1}{(1-\sum _{u=0}^{n-1}{x}_{u,j})}^2\\ & +P_3\sum _{(u,v)\notin E}\sum _{j=0}^{n-1}{x}_{u,j}{x}_{v,(j+1)\mathrm{\%}n}\end{array}$$

其中惩罚系数设定为$P_1=P_2=P_3=5$，第一项是路径成本，后三项分别对应节点约束、位置约束和边约束。

2. 模型求解

2.1 使用SA求解

使用模拟退火算法进行求解，配置了初始温度为100，降温系数为0.99，终止温度为0.001，每温度迭代次数为10。代码如下：

optimizer = kw.classical.SimulatedAnnealingOptimizer(
    initial_temperature=100,
    alpha=0.99,
    cutoff_temperature=0.001,
    iterations_per_t=10,
    size_limit=100
)

为了符合CIM真机8精度的要求，我们添加了精度缩减预处理步骤，使用PrecisionReducer将变量精度限制为8位：

optimizer = kw.cim.PrecisionReducer(optimizer, 8)
solver = kw.solver.SimpleSolver(optimizer)

求解完成后，代码验证约束满足情况和计算实际路径成本：

unsatisfied, res_dict = qubo_model.verify_constraint(sol_dict)
path_cost = kw.core.get_val(qubo_model.objective, sol_dict)

最终得到最优求解结果：

未满足约束数: 0
约束项值: {'node_cons(0,)': 0.0, 'node_cons(1,)': 0.0, 'node_cons(2,)': 0.0, 'node_cons(3,)': 0.0, 'node_cons(4,)': 0.0, 'pos_cons(0,)': 0.0, 'pos_cons(1,)': 0.0, 'pos_cons(2,)': 0.0, 'pos_cons(3,)': 0.0, 'pos_cons(4,)': 0.0, 'edge_cons': 0.0}
实际路径成本: 5.0

表示找到有效解，路径总成本为5，对应可能路径：0→3→4→1→2→0

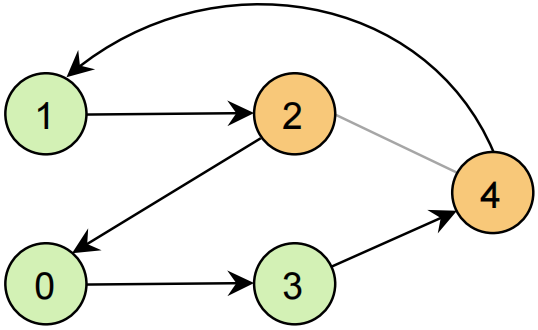路径求解

2.2 调用真机求解

最新的SDK功能已支持直接调用真机求解，只需将求解器部分替换为调用CIM真机代码。下面将对现有代码中的“配置求解器”部分进行修改，使其能够通过SimpleSolver调用CIM真机。

将以下原有代码：

# 配置求解器
optimizer = kw.classical.SimulatedAnnealingOptimizer(
    initial_temperature=100,
    alpha=0.99,
    cutoff_temperature=0.001,
    iterations_per_t=10,
    size_limit=100
)
optimizer = kw.cim.PrecisionReducer(optimizer, 8)  # 8位精度
solver = kw.solver.SimpleSolver(optimizer)

替换为：

# 配置真机求解器（调用 CIM 真机）
cim_optimizer = kw.cim.CIMOptimizer(
    user_name='test',
    password='absd1232',
    cim_task_manager_domain='local',  # 本地部署情况
    project_no='abc123'
)
solver = kw.solver.SimpleSolver(cim_optimizer)

即可实现远程真机调用。

注意，如果求解的最终结果不尽人意，可能需要考虑以下三点问题：

问题现象	可能原因	解决方案
未满足约束数>0	Penalty过小	逐步增加Penalty值
路径成本异常高	精度损失过大	降低PrecisionReducer参数
求解时间过长	温度参数不合适	调整初始温度和降温速率

将TSP问题转化为QUBO问题，通过惩罚项将约束条件融入目标函数，使得可以使用量子算法求解，模拟退火算法通过温度控制逐步收敛到较优解，并且使用精度缩减的方式使该问题能够在现有的量子计算机上运行。

3. 完整代码

import kaiwu_swig as kw
import numpy as np

def solve_tsp():
    # 定义距离矩阵
    w = np.array([[0, 0, 1, 1, 0],
                  [0, 0, 1, 0, 1],
                  [1, 1, 0, 0, 1],
                  [1, 0, 0, 0, 1],
                  [0, 1, 1, 1, 0]])

    n = w.shape[0]  # 节点数量

    # 创建 QUBO 变量矩阵 (n x n)
    x = kw.qubo.ndarray((n, n), "x", kw.qubo.Binary)

    # 生成边集合和非边集合
    edges = [(u, v) for u in range(n) for v in range(n) if w[u, v] != 0]
    no_edges = [(u, v) for u in range(n) for v in range(n) if w[u, v] == 0]

    # 定义边使用判断函数
    def is_edge_used(x, u, v):
        return kw.qubo.quicksum([x[u, j] * x[v, (j + 1) % n] for j in range(n)])

    # 初始化 QUBO 模型
    qubo_model = kw.qubo.QuboModel()

    # 设置目标函数：最小化路径成本
    path_cost = kw.qubo.quicksum([w[u, v] * is_edge_used(x, u, v) for u, v in edges])
    qubo_model.set_objective(path_cost)

    # 添加约束条件
    # 节点约束：每个节点必须占据一个位置
    qubo_model.add_constraint(x.sum(axis=0) == 1, "node_cons", penalty=5)

    # 位置约束：每个位置必须有一个节点
    qubo_model.add_constraint(x.sum(axis=1) == 1, "pos_cons", penalty=5)

    # 边约束：非连接边不得出现
    qubo_model.add_constraint(
        kw.qubo.quicksum([is_edge_used(x, u, v) for u, v in no_edges]),
        "edge_cons", penalty=5
    )

    # 配置求解器
    optimizer = kw.classical.SimulatedAnnealingOptimizer(
        initial_temperature=100,
        alpha=0.99,
        cutoff_temperature=0.001,
        iterations_per_t=10,
        size_limit=100
    )
    optimizer = kw.cim.PrecisionReducer(optimizer, 8)  # 8位精度
    solver = kw.solver.SimpleSolver(optimizer)

    # 求解问题
    sol_dict, qubo_val = solver.solve_qubo(qubo_model)

    # 验证结果
    unsatisfied, res_dict = qubo_model.verify_constraint(sol_dict)
    print(f"未满足约束数: {unsatisfied}")
    print(f"约束项值: {res_dict}")

    # 计算路径成本
    path_cost = kw.core.get_val(qubo_model.objective, sol_dict)
    print(f"实际路径成本: {path_cost}")

if __name__ == "__main__":
    solve_tsp()