基于相干光量子计算的反欺诈与反洗钱社区发现算法
随着金融科技的不断发展，数字科技与金融业融合的同时也伴随着金融欺诈风险的不断扩大。当前，洗钱和金融诈骗等犯罪行为愈发频繁，其手法趋向专业化、团伙化，隐蔽化。面对诈骗手法的不断演变，传统的反欺诈技术面临维度单一、效率低下和范围受限等挑战。
本项目通过构建量子社区发现算法并使用相干光量子计算机进行求解，应用于商业银行反洗钱业务场景，在图数据的基础上运用量子算法进一步赋能。结果表明，量子社区发现算法不仅效率更高，同时模型ks指标优于传统社区发现算法，有助于商业银行等金融机构进一步提高反洗钱业务能力。
1. 项目描述
近年来，网络诈骗、地下钱庄、非法集资等跨行业、涉众型洗钱相关犯罪持续高发，一些新业态如区块链、虚拟货币等常被用于洗钱活动，对金融安全、社会稳定造成严重影响。仅北京市一起通过交易虚拟货币为地下钱庄洗钱的案件，涉案资金就超过20亿元人民币。目前，国家机关和各金融机构都积极通过监管、新型技术等手段，努力减少这类犯罪行为带来的损失。
以商业银行针对地下钱庄的反洗钱业务实践来看，诈骗团伙的资金链条一般呈现上游、中游、下游三个环节，每一环节均对应一组账户，在不同时间段被用于资金流转的不同环节。由于诈骗团伙成员遍布各地，同时段分散使用多个商业银行账户，且与赌博、腐败等犯罪相互交织，交易追踪难度大。目前运用社区发现的思路对反洗钱业务中的异常交易进行探测，已成为商业银行的重要方法之一。具体形式为：将每个账户看作一个节点，当账户存在转账或交易等行为时，该账户节点之间就会存在一条边，也就构建起了一个图谱，形成一个关系网络，从而可以使用社区发现算法进行异常团体的识别。然而，面对复杂的客户流水数据，如何高效的从中获取有价值的信息，更好的对账户进行社区划分，是目前传统社区发现算法亟待突破的难题。
相干光量子计算机以光量子比特作为基本单位，模拟伊辛模型（伊辛模型在数学上等价于QUBO模型）的演化过程。专用于求解大规模组合优化类问题，已被证实可有效求解NP-hard问题，并且具有相比经典计算指数级的加速优势和更高的最优解求解概率。本项目针对商业银行反洗钱“地下钱庄”监测场景，构建量子的社区发现算法，并使用相干光量子计算机进行求解。结果表明，相比传统社区发现算法，量子算法效率更高且社区划分结果更好，使得银行能更准确地基于交易流水对社区进行分类，尤其是可疑“犯罪分子”聚集的社区，为反洗钱场景提供新的技术手段。
2. 问题描述
问题： 应用基于模块度的社区发现算法，将每个账户看作一个图网络中的一个节点，账户之间的交易关系看作图中的一个边。我们需要将每个节点归类到相应的社区中，使得社区内的权重最大，而社区间的权重最小。
目标： 最小化社区之间的权重同时最大化社区内节点的权重。
3. 建模过程
模块度是一种衡量社区划分质量的指标，多被应用在基于优化的社区发现方法中。 模块度反映了网络中的社区划分是否合理，即社区内部的连接是否比随机情况下更为紧密。如果划分的社区内部有较多的边，社区之间有较少的边，则该社区对应的模块度较大。
因此，可以将社区发现问题转换为最大化模块度问题。模块度的公式如下：
为转化成QUBO模型我们需要定义二值决策变量
因此，社区
对于任意节点
转化为QUBO模型为：
4. 结果
本项目采用了公开的6000个账户的交易和静态信息， 覆盖816,270条交易记录和132,121个交易对手方，且账户之间没有相互交易记录。 结果表明，通过使用量子社区发现算法基于对手+渠道+摘要构成异构图，模型的模块度与KS指标相较于传统社区算法均有明显提升。
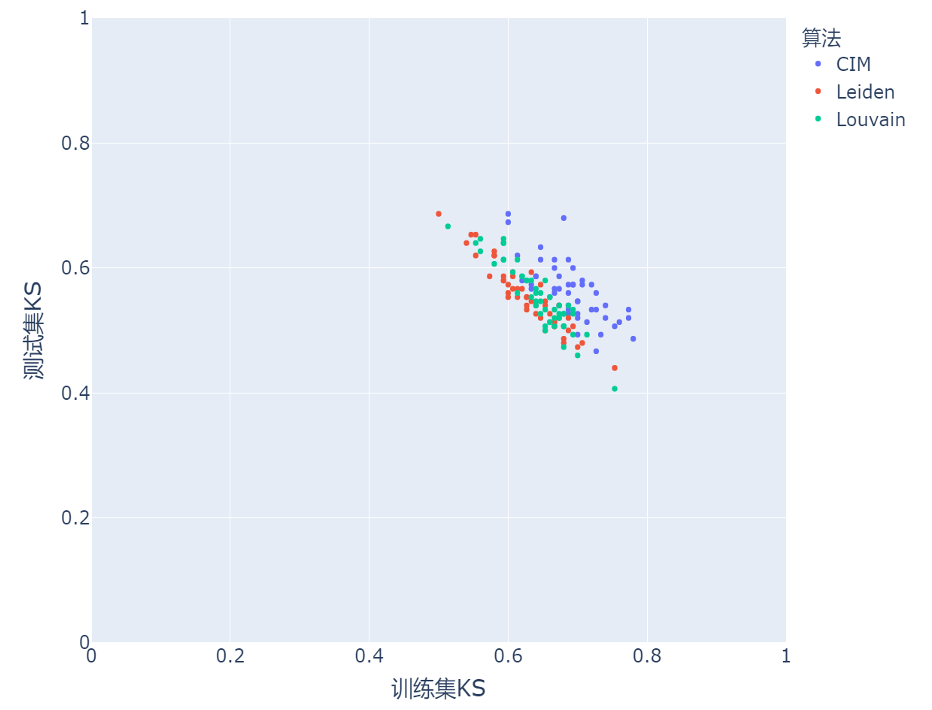图1：量子社区发现算法结果 并且，在合理阈值过滤下，社区发现模块度和模型KS指标存在正向关系。在cutoff为40%时，量子社区发现算法的结果优于传统Louvain算法（红框内的为量子算法结果，其余为Louvain结果）。
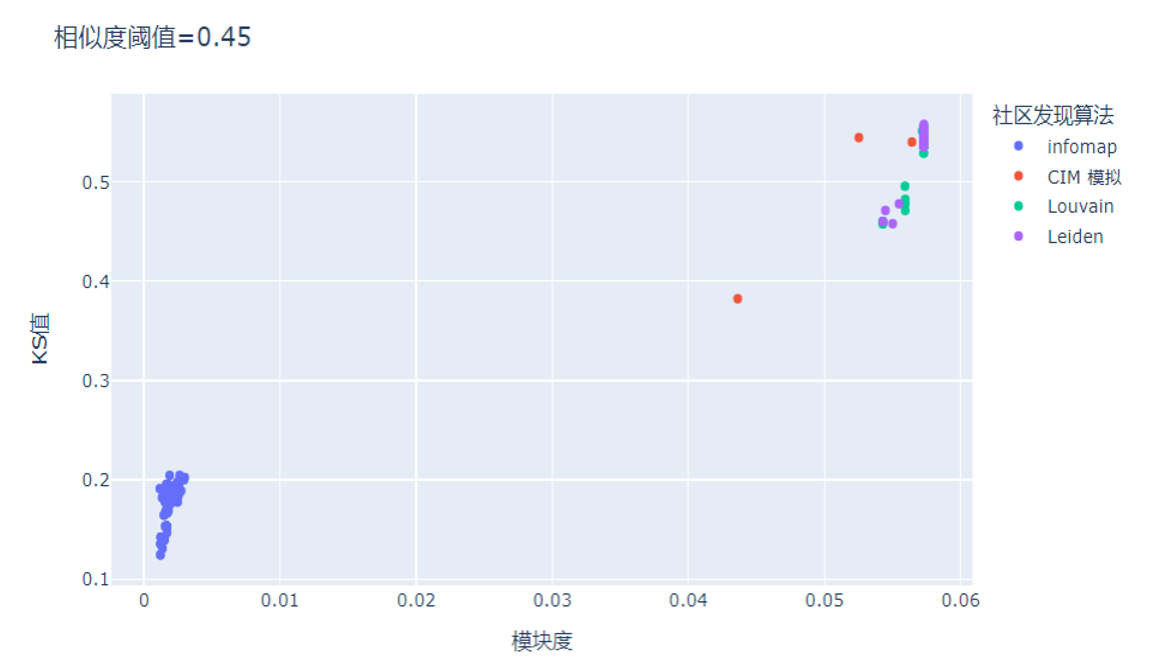图2：量子社区发现算法与Louvain算法对比 通过对比1200个交易账户下量子社区发现和传统社区发现Louvain算法的结果，我们可以发现，量子社区发现算法显示出更稳定的业务效果，并能够预设社区数量，避免了社区划分连接质量差的问题，以及大量小社区的出现，增加了模型的鲁棒性。这同时也证明了QUBO建模社区发现在交易图上的可行性和优势。并且随着量子比特数的增加，该算法在处理社区发现反洗钱问题上可以实现有效的加速。
| 模块度 | Group_id | 社区内账户数量 | 社区整体欺诈概率 |
|---|---|---|---|
| 0.056421 | 1 | 458 | 7.9% |
| 0.056421 | 6 | 408 | 55.6% |
| 0.056421 | 3 | 140 | 12.1% |
| 0.056421 | -1 | 114 | 12.3% |
| 0.056421 | 5 | 36 | 13.9% |
| 0.056421 | 7 | 16 | 0.0% |
| 0.056421 | 4 | 10 | 0.0% |
| 0.056421 | 8 | 10 | 0.0% |
| 0.056421 | 2 | 8 | 12.5% |
表1：量子社区发现结果
| 模块度 | Group_id | 社区内账户数量 | 社区整体欺诈概率 |
|---|---|---|---|
| 0.057309 | 6 | 482 | 7.1% |
| 0.057309 | 7 | 412 | 55.1% |
| 0.057309 | 4 | 160 | 13.8% |
| 0.057309 | -1 | 114 | 12.3% |
| 0.057309 | 3 | 14 | 21.4% |
| 0.057309 | 5 | 10 | 0.0% |
| 0.057309 | 0 | 4 | 0.0% |
| 0.057309 | 1 | 2 | 0.0% |
| 0.057309 | 2 | 2 | 0.0% |
表2：Louvain算法结果
5. 场景延展
社区发现算法能够将社会关系、道路交通等网络中的个体分组并组成社区结构，进而揭示网络中隐藏的模式和结构，帮助研究人员和从业者分析和理解复杂网络的深层次结构信息。未来，社区发现算法也将在多个领域被广泛的应用：
在金融风险控制领域，基于交易网络拓扑的社区发现能够有效识别异常资金流动模式。通过构建账户节点间包括交易频次、金额波动、时间序列相关性等特征的多维度关联网络，算法可检测出具有异常紧密连接的资金群落，此类群落往往与信用卡套现、洗钱链条等金融犯罪活动存在显著相关性，为反欺诈系统提供基于网络结构的早期预警信号。
对于社交网络分析，社区发现技术能够通过挖掘用户互动网络的隐含结构，识别具有共同行为特征或兴趣偏好的用户群体，为个性化的智能推荐系统提供帮助。
而在生物分子网络分析方面，社区发现算法通过检测高度互连的蛋白质子网络，发现参与特定代谢通路或细胞过程的蛋白质集群，为疾病靶点发现和药物作用机制研究提供新的分析维度。
论文链接：QuantumComputing in Community Detection for Anti-Fraud Applications